基于改进BP神经网络的多层土壤湿度反演

刘 娣，孙佳倩，余钟波，4

（1.河海大学 水灾害防御全国重点实验室，南京 210024；2.河海大学水文水资源学院，南京 210024；3.河海大学全球变化与水循环国际合作联合实验室，南京 210024；4.长江保护与绿色发展研究院，南京 210024）

0 引 言

土壤湿度（Soil Moisture, SM）指土壤的含水量，通过改变地表反射率、地表蒸散发过程、陆面植被的生长状况、蒸散发过程以及能量输送过程等方式影响蒸散发、通量等物理过程，进而影响陆地与大气之间的耦合及水分和能量交换，给气候变化带来影响[1]。通过机器学习反演获取高精度表层至深层土壤湿度数据，对研究气候预报、水文模型模拟预报、干旱监测[2]、农作物生长[3]等具有重要意义。

机器学习被广泛应用于水文领域的研究中。其中BP 神经网络（Back Propagation Neuron Network，BPNN）因具有较强的非线性映射能力、自适应能力和泛化能力，被大量的应用于土壤湿度反演的工作中[4,5]。但随着研究的深入，BP 神经网络也展现出较强的随机性和不确定性，存在不能保证收敛到全局最小点等问题[6]。使用天牛须搜索算法（Beetle Antennae Search Algorithm, BAS）对BP 神经网络进行改进是目前一个新的研究方向，李琪等[7]使用BAS-BP模型对钻井钻速进行预测，结果表明BAS-BP具有良好的收敛性和搜索能力且预测效果优于BP、PSO-BP 及GA-BP。徐轟钊等[8]建立了BAS-BP 柴油机故障诊断和识别模型，证明了BAS-BP 模型在各方面都优于PSO-BP 和GA-BP 模型，且BAS-BP 的故障分类准确率可达到98.90%。但目前BAS-BP模型在反演土壤湿度的适用性领域还缺乏具体的研究。

机器学习模型是黑箱模型，主要是利用已有的指标对结果进行评价，不能自主选择输入变量。考虑到气象因子与土壤湿度之间存在互馈效应[9-12]，迟凯歌等[13]利用主成分分析法辨识了影响流域NDVI 变化的主导气候因素，并在此基础上构建了BP 神经网络，证明因子筛选能够显著提高模型精度。李柳阳等[14]基于站点观测的10cm 深度土壤湿度数据和8 个气象数据，通过主成分分析法选取温度、日照时间、降水、风速及相对湿度作为线性回归和BP 神经网络模型的输入数据，构建BP神经网络模型。

本文基于BP 神经网络，利用有限气象站点观测数据进行驱动，构建适应于不同深度土壤湿度反演的BP 神经网络模型。采用天牛须搜索算法（Beetle Antennae Search Algorithm，BAS）对BP 神经网络进行改进，构建BAS-BP 神经网络模型（Beetle Antennae Search-Back Propagation Neural Networks），验证BAS-BP模型对不同区域不同深度土壤湿度的反演效果。

1 研究方法

1.1 主成分分析方法

主成分分析法是目前最常用的线性降维方法之一，其核心思想是利用某种线性投影，将高维度的数据映射到低维度的空间当中[19]，使投影到低维度上数据信息在降低维数的同时能够尽可能的保留原数据的信息，达到使用少数具有代表性数据代替多个原始变量的目的。其主要原理如下[20]：

（1）对由n维相关变量组成的原始变量集X进行z分数（z-score）标准化处理，得到均值为0、方差为1 的标准化矩阵ZX。

（2）基于标准化矩阵ZX建立协方差矩阵R，利用特征值分解法求解标准化矩阵ZX的特征值并将其从大到小排列，得到特征值λk(k=1,2,…,n)、特征向量Gk与主成分Fk。

（3）根据方差贡献率和累计方差贡献率确定主成分。

1.2 BP神经网络

BP 神经网络是1986 年由Rumelhart 和McCelland 团队提出来的机器学习方法，是一种按误差逆传播算法训练的多层前馈网络，由输入层、隐藏层和输出层组成。其核心思想是利用负梯度下降算法，将误差控制在设计的范围之内，再将误差的变化量反向传播到神经网络的每一层，进而调整每一层神经网络的参数值，通过多次迭代之后，误差就会稳定在一定的范围内[21,22]，使最终输出结果接近期望值。

1.3 天牛须搜索算法

天牛须搜索算法BAS 是在2017 年提出的一种受到生物启发的智能优化算法，具有搜索速度快、实施便捷、不依赖目标函数的具体形式和梯度信息即可实现寻优计算等优点[23]。神经网络随机生成初始连接权值和阈值，会对BP 神经网络的收敛速度和泛化能力产生影响，使用天牛须搜索算法对BP 神经网络的初始权值和阈值进行优化重构，可以减少BP 神经网络的运行时间，提高收敛速度和稳定性。其基本步骤如下[24]。

（1）建立并初始化BP 神经网络，获取网络初始权值和阈值。

（2）设置初始步长和迭代次数，对天牛须搜索算法进行初始化，创建天牛须朝向的随机向量且做归一化处理，创建天牛左右须空间坐标。

（3）将BP 神经网络的初始权值和阈值分别设置为天牛须的方向与初始位置。

（4）通过计算适应度函数值判断天牛左右两须所感知到的气味浓度。

（5）进行探寻气味、前进操作：利用自适应函数计算左右两须感知的气味浓度，如果左边触角感知到的气味浓度比右边强，则天牛下一步向左边前进，如果右边触须感知到的气味浓度比左边强，则天牛下一步向右边前进。

（6）判断是否达到迭代终止条件，即天牛是否找到食物，亦即输出的权值与阈值是否为全局最优解。若是全局最优解则停止迭代；否则返回步骤（3）。

（7）获得最优权值和阈值后，将其赋值给BP 神经网络，得到BAS-BP神经网络模型。

1.4 评估指标

本文采用均方根误差（Root Mean Squared Error，RMSE）、平均绝对误差（Mean Absolute Error，MAE）、相关系数（Correlation Coefficient，R）对BP 及BAS-BP 模型的反演效果进行评估，RMSE和MAE越小，R越大，反演效果越优。

本文技术路线如图1所示。首先，采用主成分分析法筛选出有效气象观测数据作为驱动，构建不同深度土壤湿度BP 神经网络模型；其次，利用天牛须搜索算法对BP 神经网络模型进行改进，构建不同深度土壤湿度BAS-BP神经网络模型；最后，综合利用统计分析指标评估不同模型的反演效果。主成分分析方法、BP 神经网络模型、天牛须搜索算法及评估指标介绍如下。

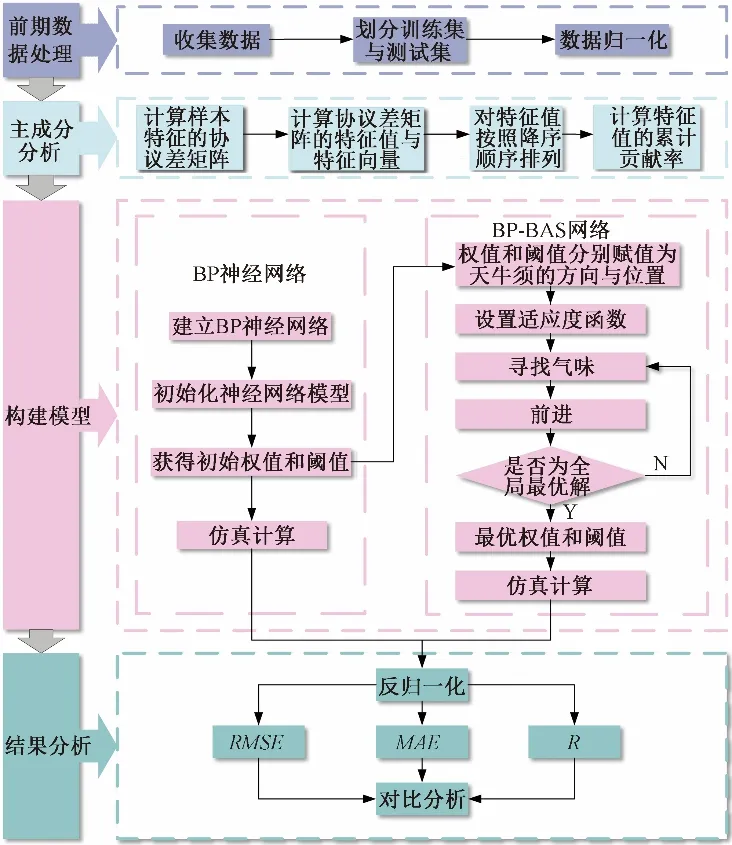
图1 技术路线Fig.1 Technology route

2 模型构建及实例分析

本研究数据资料选自美国南卡罗来纳州(South Carolina)的McClellanville 站(北纬33°5′20.23″，西径79°28′2.23″)和青藏高原野外观测站MAWORS（Muztagh Ata Westerly Observation and Research Station，慕士塔格西风带环境综合观测研究站）(北纬38°24′30.26″，东经75°2′21.31″)的站点观测数据。在McClellanville 站，选用2010年1月1日-2013年12月31日的实测数据，共计4 a 的有效数据进行训练与模拟。所选数据要素包括平均降雨量、相对湿度、气温、太阳能、红外表面温度、土壤温度以及土壤湿度。将2010 年1 月1 日-2012 年12 月31日（1 096 d）的数据作为训练集建立模型，将2013年1月1日-2013 年12 月31 日（365 d）的数据作为测试集检验模型的反演精度。在MAWORS 站，由于观测数据资料序列缺失较多，选用2012 年1 月1 日-2016 年12 月31 日的多年日平均数据（共计365 d）进行训练与模拟，所选数据包括气象数据、地表辐射数据、EC数据、土壤温度、土壤湿度。将第1～250 d 的数据作为训练集建立模型，第251～365 d 的数据作为测试集检验模型的反演精度。各站的数据资料如表1所示，各要素时间序列如图2所示。

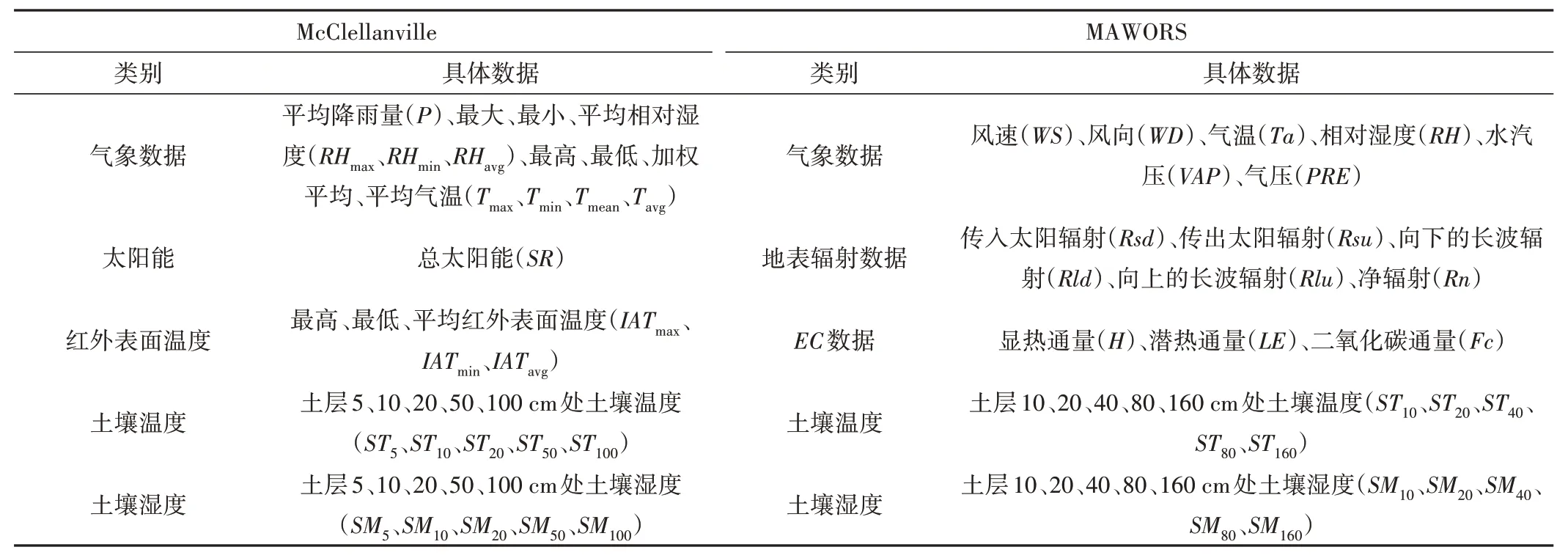
表1 McClellanville和MAWORS站数据资料Tab.1 McClellanville and MAWORS station data information

图2 研究数据时间序列Fig.2 Time series of the hydroclimate variables

2.1 主成分分析

通过MATLAB 中的pca 函数和wmspca 函数，计算各项特征因子与所选因子之间的相关性进而选取不同深度土壤湿度的主成分（表2）。在反演不同深度土壤湿度时，使用表中相应的主成分作为输入数据，对应的土壤湿度作为输出数据，分别利用BP 神经网络和BAS-BP 神经网络建立反演模型。根据不同土壤深度对应的主成分计算得到BP 和BAS-BP 模型对McClellanville 站和MAWORS 站训练集和测试集不同深度土壤湿度的反演值与观测值的RMSE、MAE及R如表3所示。

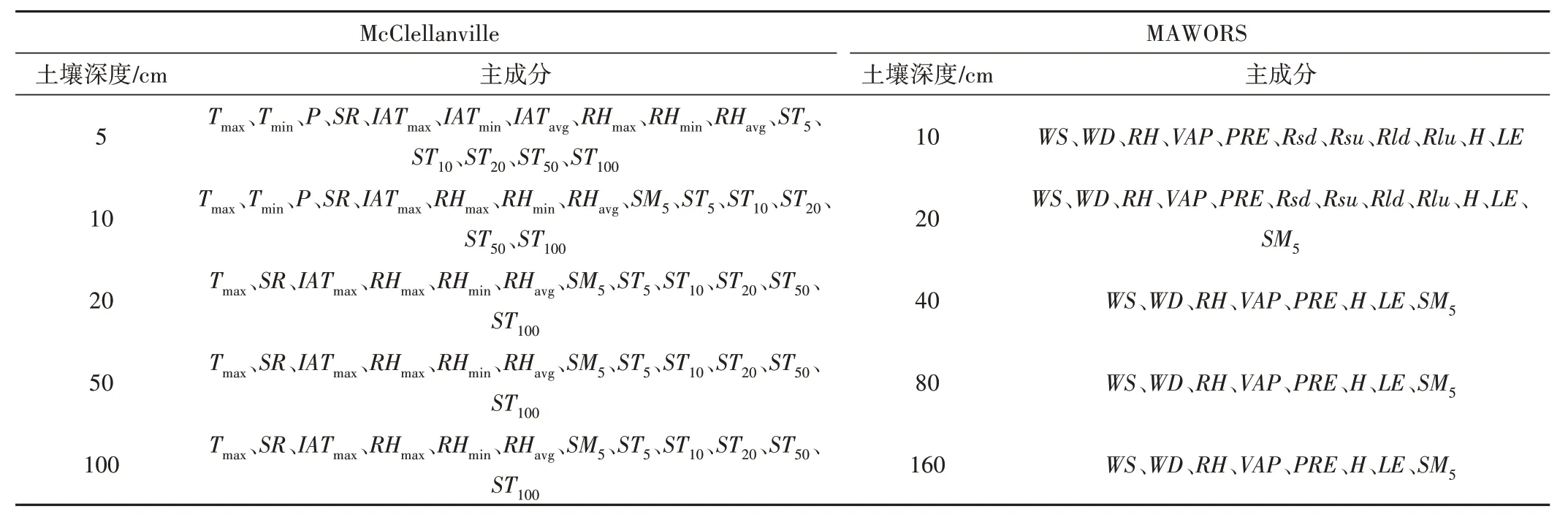
表2 McClellanville站与MAWORS站主成分分析结果Tab.2 Results of principal component analysis for McClellanville and MAWORS stations

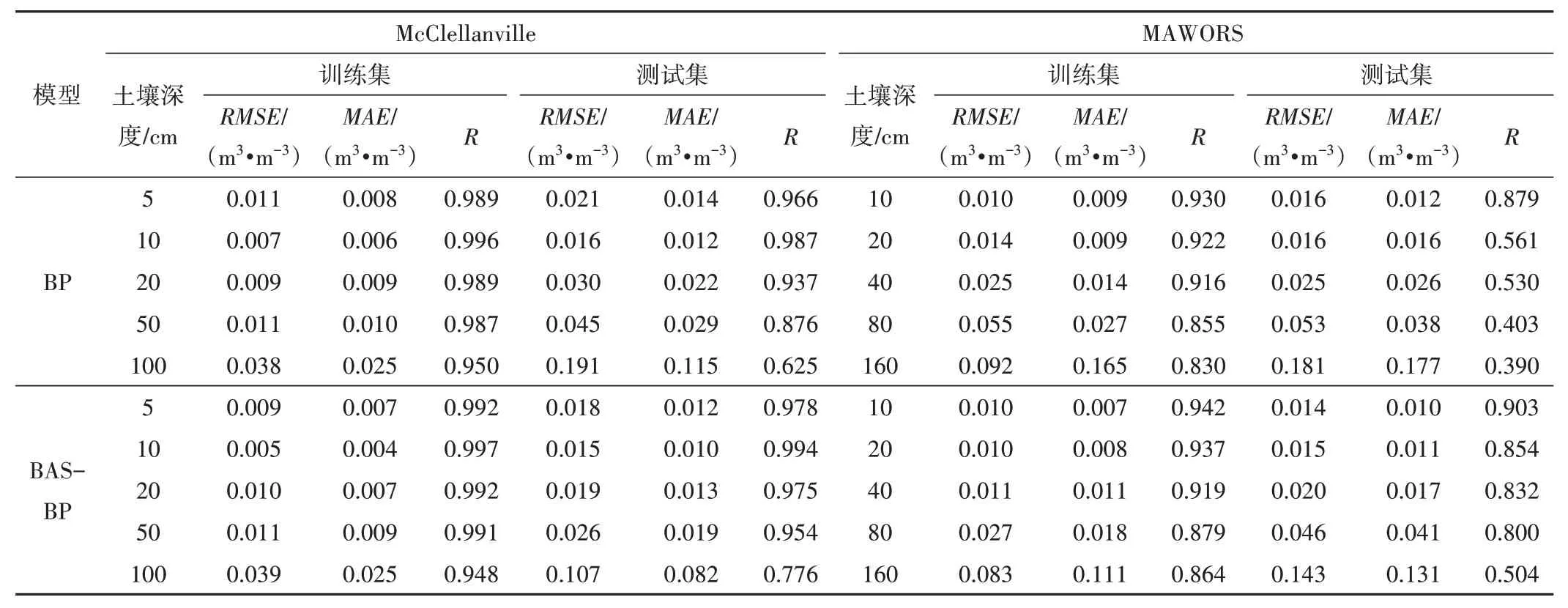
表3 BP、BAS-BP模型对各站各层土壤湿度反演的均方根误差（RMSE）、平均绝对误差（MAE）及相关系数（R）Tab.3 The RMSE, MAE, and R of BP and BAS-BP models for the inversion of soil moisture in each layer at each station

2.2 反演结果分析

2.2.1 训练集与测试集对比分析

由表3可知，BP和BAS-BP模型对各站训练集的不同深度土壤湿度的反演效果较好，证实构建的BP 和BAS-BP 模型适应于各站不同深度土壤湿度的反演。其中，在McClellanville站，各模型反演的各层土壤湿度的RMSE范围为0.005～0.039 m3/m3，MAE范围为0.004～0.025 m3/m3，R范围为0.948～0.997；在MAROWS 站，各模型反演的各层土壤湿度的RMSE范围为0.010～0.092 m3/m3，MAE范围为0.007～0.165 m3/m3，R范围为0.830～0.942。

McClellanville 站各模型反演的各层土壤湿度的RMSE范围为0.015～0.191 m3/m3，MAE范围为0.010～0.115 m3/m3，R范围为0.625～0.994；在MAROWS 站，各模型反演的各层土壤湿度的RMSE范围为0.014～0.181 m3/m3，MAE范围为0.010～0.177 m3/m3，R范围为0.390～0.903。通过对比分析，BP 和BAS-BP模型对各站训练集不同深度土壤湿度的反演效果均优于测试集，主要体现在训练集各模型反演的各站不同深度土壤湿度的RMSE和MAE均略低于相同深度的测试集，而R均略高于相同深度的测试集。

2.2.2 不同深度土壤湿度反演结果对比

通过对比分析，在测试集，BP 和BAS-BP 模型对各站不同深度土壤湿度的反演效果在表层（SM5、SM10） 及中层（SM20、SM40、SM50）较优且均在表层SM10达到最佳，而随着土壤深度的增加（SM80、SM100、SM160），各模型对各站深层土壤湿度的模拟能力呈减弱趋势。主要体现在各站各模型在SM10处的RMSE与MAE量值较其余土壤深度最低，而R最高。随着土壤深度的增加，反演的表层土壤湿度的RMSE和MAE低于深层土壤，而R高于深层土壤。例如，在McClellanville站，BAS-BP 模型在SM5和SM10的RMSE和MAE分别为0.018 m3/m3、0.012 m3/m3和0.015 m3/m3、0.010 m3/m3，而R分别为0.978、0.994。随着土壤深度的增加，BAS-BP 模型的反演效果逐渐减弱，在SM20、SM50及SM100的RMSE增加至0.019 m3/m3、 0.026 m3/m3、 0.107 m3/m3，MAE增加至0.013 m3/m3、0.019 m3/m3、0.082 m3/m3，R下降为0.975、0.954、0.776。BP模型对McClellanville 站测试集的反演效果与此一致。在MAWORS 站，BP 模型在SM10和SM20的RMSE和MAE分别为0.016 m3/m3、0.012 m3/m3和0.016 m3/m3、0.016 m3/m3，而R分别为0.879、0.561。随着土壤深度的增加，BAS-BP 模型的反演效果逐渐减弱，在SM20、SM50及SM100的RMSE增加至0.025 m3/m3、0.053 m3/m3、0.181 m3/m3，MAE增加至0.026 m3/m3、0.038 m3/m3、0.177 m3/m3，R下降为0.530、0.403、0.390。BAS-BP模型对MAWORS站测试集的反演效果与此一致。

2.2.3 BP与BAS-BP模型反演精度对比分析

综合统计分析指标（表3）及对比图（图3）和离差图（图4），BAS-BP 模型对各站各层土壤湿度的反演效果均优于同一土壤深度的BP 模型。在测试集，BAS-BP 模型在各站反演的各层土壤湿度的RMSE与MAE均低于BP 模型，而R均高于BP模型。例如，在MAWORS站，BP与BAS-BP模型在SM10处的RMSE和MAE分别为0.016 m3/m3、0.014 m3/m3和0.012 m3/m3、0.010 m3/m3，R分别为0.879、0.903。在SM160处的RMSE和MAE分别为0.181、0.143 和0.177、0.131，R分别为0.390、0.504。此外，BAS-BP模型对各站不同深度土壤湿度发反演值与观测值时间序列拟合性更好（图3），偏差较小（图4）。以上结果表明，通过天牛须搜索算法优化的BP 模型有效提高了表层至深层土壤湿度的反演能力，BAS-BP 模型稳定性与适配性更优。

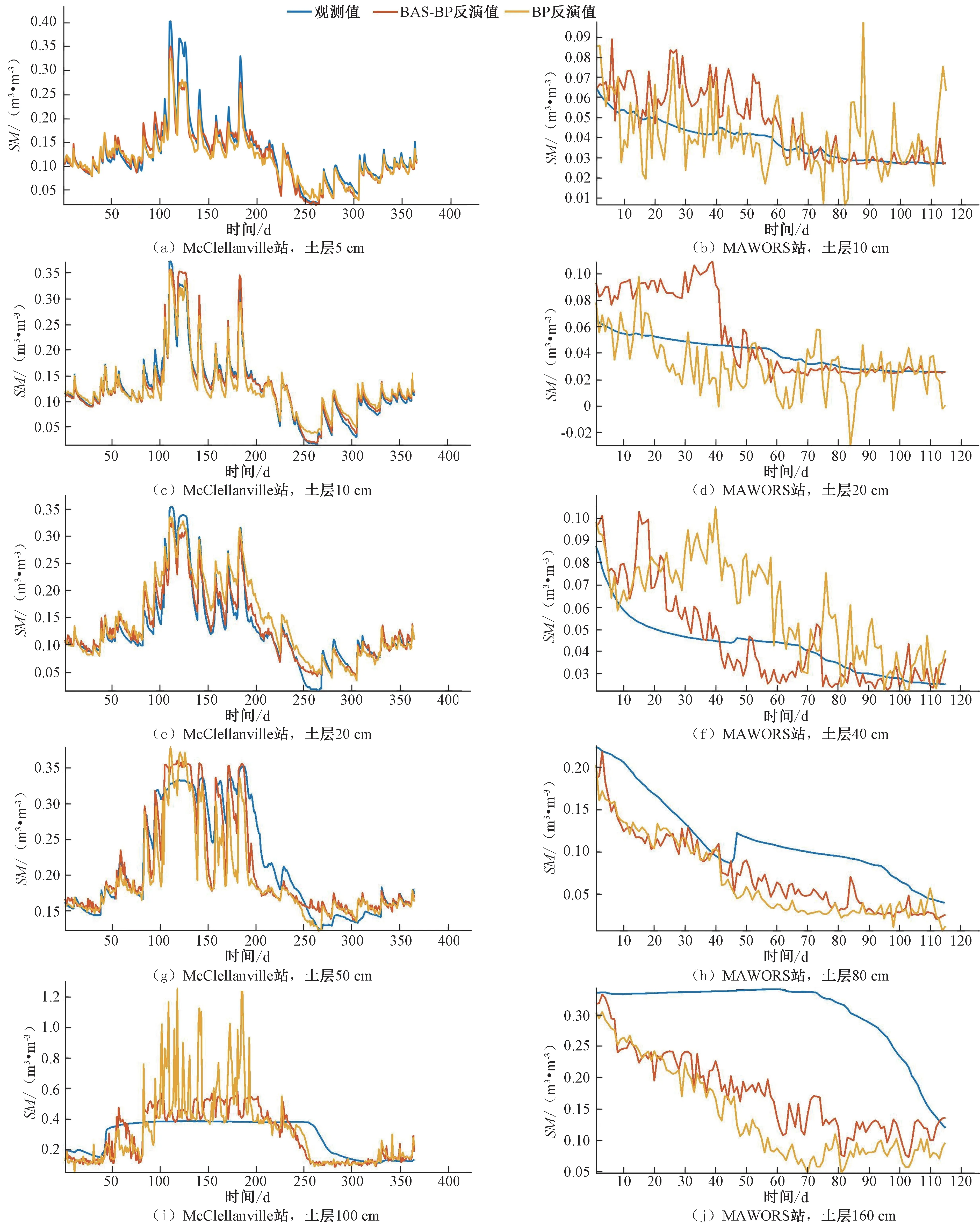
图3 基于BAS-BP模型、BP模型反演不同深度土壤湿度与观测值对比图Fig.3 Comparison of soil moisture at different depths with observed values based on BAS-BP model and BP model inversion

3 讨 论

3.1 不同机器学习模型精度分析

目前，土壤湿度反演常用的机器学习方法有BP 神经网络、随机森林（Random Forest，RF）、支持向量机（Support Vector Machine， SVM）、 极限学习机（Extreme LearningMachine, ELM）、广义回归神经网络（Generalized Regression Neural Network，GRNN）[26-28]等。相较于BP 神经网络、GRNN、ELM 和SVM 模型，RF 模型在土壤湿度反演中的稳定性更好，精度更高[29-32]。然而，原始机器学习模型的预测效果易受外界影响。越来越多的研究聚焦于模型参数的优化，例如，利用遗传算法(Genetic Algorithm, GA)、粒子群算法(Particle Swarm Optimization, PSO)、 蚁群算法(Ant Colony Algorithm, ACA)、天牛须搜索算法、二次移动平均法(Double Moving Average， DMA)、 变分模态分解(Variational Mode Decomposition，VMD)、灰狼优化算法（Grey Wolf Optimizer，GWO）算法等对机器学习模型进行优化重构[33-35]，优化后的模型能克服原始模型的缺点，具有更强的稳定性和拟合能力，可以大幅提高模型计算精度。在众多优化机器学习的算法中，BAS具有原理简单、参数少、计算量少等优点，现有研究[7,8,36]表明基于BAS 优化的机器学习模型的计算精度和稳定性均优于GA、PSO 等算法。然而，将BAS-BP 神经网络模型用于土壤湿度反演的研究鲜有报道。因而，本文尝试使用BAS 算法对BP 神经网络进行优化，构建BAS-BP 神经网络模型，验证其在不同深度土壤湿度反演中的效能。研究结果表明，基于BAS-BP 神经网络模型显著提高了BP 神经网络模型在表层至深层土壤湿度的反演能力。

3.2 不同深度土壤湿度反演精度分析

由于土壤中各种物理过程的热力和水力结构特性，使得土壤过程相较于大气的变化更为缓慢，从而使得土壤湿度具有一定“记忆性”。赵家臻等[25]利用中国气象局国家气象信息数据，通过比较皮尔逊相关法和自相关法计算，量化了土壤湿度的记忆能力，结果显示随着土壤深度的增加，土壤湿度的记忆性也显著增强。表层土壤湿度受到大气的影响最为直接，土壤记忆性较短，使用机器学习方法反演得到的土壤湿度精度较高。随着土层向下延伸，土壤湿度的记忆性增强，其变化过程相较于大气变化更加缓慢，反演得到的土壤湿度精度随之下降。因此，两个站均在表层土壤10 cm 处土壤湿度的反演效果最佳，随着土壤湿度的增加，反演精度逐渐下降，在深层土壤100 cm以及160 cm处反演精度最差。

3.3 影响机器学习模型反演效果因素分析

通过对比分析，McClellanville 站的反演效果更佳，使用BP 和BAS-BP 模型相关系数R的变化幅度分别为10.789%、5.061%，MAWORS 站使用BP 和BAS-BP 模型相关系数R的变化幅度分别为38.531%、14.624%，BP 和BAS-BP 模型对McClellanville 站各层土壤湿度的反演效果均优于MAWORS站，这主要归因于地理条件及数据资料等因素。青藏高原是我国最大、海拔最高的高原，被誉为“亚洲水塔”。然而，由于环境条件恶劣、海拔高、地形复杂、地表不均等诸多因素，青藏高原的水文气象观测站点较为稀少，观测数据有限。这些因素对机器学习模型的反演性能影响较大。

4 结 论

本文采用天牛须搜索算法对BP 神经网络进行优化，构建BAS-BP 神经网络模型。 选用美国南卡罗来纳州的McClellanville 站及青藏高原MAWORS 站水文气象观测数据，利用主成分分析法筛选土壤湿度反演的驱动因子作为BP 及BAS-BP模型的输入数据，分别构建BP及BAS-BP模型，对不同深度土壤湿度进行反演。主要结论如下：

（1）BP 及BAS-BP 模型适应于各站点表层至深层土壤湿度的反演，其对训练集的反演效果优于测试集。

（2）融合天牛须搜索算法优化的BAS-BP 模型优于BP 模型。BAS-BP 模型可以有效提高表层至深层土壤湿度的反演精度，稳定性与适配性更优。

（3）BP 与BAS-BP 模型均在SM10反演效果最佳。随着土壤深度增加，反演效果减弱。在SM100和SM160，BP 与BAS-BP模型反演效果最低。在相同条件下，BAS-BP 模型始终优于BP模型。

（4）青藏高原受到环境、海拔、地形、地表等诸多因素的影响，站点观测数据质量略有不足，BP 及BP-BAS 模型对MAWORS站各层土壤湿度的反演效果略低于McClellanville站。