基于非高斯性的莺歌海盆地鬼波压制方法研究*

吴耀乐

中海油田服务股份有限公司物探事业部特普公司，广东 湛江 524057

鬼波在地震剖面上的表现使地震剖面同相轴增多，不利于目的层同相轴的确定［1］。在地震子波的传播过程中，鬼波对地震子波改造现象比较明显。鬼波的存在会使一次波的振幅受到影响，在地震剖面上可能会产生虚假的同相轴，严重影响地震剖面的分辨率［2，3］。特别是对于后期的地震资料解释工作来说，压制鬼波对子波的改造作用有利于提高地震资料解释结果的可信度［4，5］。在鬼波压制方法的发展中，最早的线性滤波方法是由Lindsey等人提出的［6］；Adriana、James 等人提出可以基于格林函数理论进行鬼波的压制的方法［7，8］，而且在实际海底电缆资料中得到了成功地实践。国内的李洪建等深化发展了基于格林函数理论的波场预测和鬼波压制方法［9］。目前的压制鬼波的方法在深水领域取得了不错的效果，但在浅水区还没有取得理想的压制效果［10，11］。本文通过对鬼波的形成机理以及对子波改造机理进行进一步的分析和研究，寻求更好的解决浅水鬼波效应的方法。

1 原理及方法

1.1 建立目标函数的理论依据

鬼波实际上就是在一次波上附加一个时延和进行一个幅值尺度的变换，所以鬼波和一次波有很强的相似性。直观上来看，鬼波和一次波形状是“相似”的，他们的广义高斯分布的r值相同，进而他们的峰度值也相同，因此鬼波信号和一次波信号具有相同的非高斯性。考虑到他们的r 相同，于是鬼波和一次波是具有相同分布的非高斯性随机信号［13，14］。

中心极限定理表明：如果相互独立的具有相同分布的随机信号ξ1,ξ2,...,ξk的均值和方差均存在，则他们的和比单个随机变量更趋近于高斯分布的性质［15，16］。

独立成分分析中，独立性与非高斯性等价［17，18］，又因为一次波信号和鬼波信号都具有非高斯性而且同分布，因此一次波信号和鬼波信号是独立同分布的，而且它们的均值和方差都是存在的。所以根据上述的中心极限定理可以得出：一次波与鬼波的和也就是实际接收到的观测信号比单独的一次波更加趋近于高斯分布。换一句话说就是：一次波信号比实际接收到的观测信号有更强的非高斯性。这个就是本文用非高斯性最大化的方法压制鬼波的理论依据。

本文认为一次波信号具有最大的非高斯性。对于只存在一种鬼波的情况，根据这一假设，可以建立如下的最优化模型的目标函数：

在同时存在三种鬼波的情况下，本文建立的最优化模型的目标函数为：

1.2 参数的搜索范围

鬼波最重要的两个参数是鬼波时延和海面反射系数［19，20］。虽然不知道鬼波时延和海面反射系数这两个参数的准确值。但是可以首先估计出他们大概所在的范围，然后给出这两个参数的搜索范围和搜索步长，再用参数搜索的方法，选取使目标函数达到非高斯性最大化的那一组参数作为最优的一组参数。

由于海面是强反射面，而地震波在海面发生反射的时候会发生一个180 度的相移，所以海面反射系数α是负值，而且接近于-1，即-1＜α＜0。于是本文可以设置海面反射系数的参数搜索范围：

其中αl表示α 搜索范围的下限，αh代表α 搜索范围的上限。一般情况下可以取al=-1，ah=-0.6or-0.8。

先考虑只存在一种接收点鬼波的情况。本文可以先粗略的估计出一个接收点鬼波时延：

其中d1是检波器在海面以下的沉放深度，v是地震波在海里的传播速度。于是本文可以将鬼波时延的搜索范围设置在：

其中α 是时延搜索的尺度参数，α 的值可以根据实际情况来设定。

1.3 非高斯性最大化准则

由于这个最优化问题要最大化目标函数的非高斯性，所以需要寻找一个准则来度量非高斯性。好的准则能够在处理实际地震资料中准确的反映数据的非高斯性，能够让本文准确的估计鬼波参数。反之，如果准则选取不合适，会造成鬼波时延和海面反射系数估计结果的误差较大，从而影响鬼波压制的效果。

经过反复试验，本文寻找到一种较好的度量非高斯性的准则，对噪声也不敏感：

其中y(t)是待求的随机信号，qi[yi（t）]是对yi（t）归一化后的值，L[y（t）]是本文应用的新准则的数学符号。方便起见，下文简称为L准则。而qi[yi（t）]为：

1.4 最优化模型的建立

有了目标函数、搜索范围和度量非高斯性最大化的准则，就可以将鬼波压制这个问题转化成为一个完整的最优化的问题。

对于只存在一种鬼波的情况，最优化问题变为：

其中α 的取值以及这两个参数的搜索步长需根据实际情况来设定。

对于存在三种鬼波的情况，最优化问题变为：

其中α，β 的取值以及这三个参数的搜索步长也需要根据实际情况来设定。

在处理实际的鬼波问题时，本文先将问题转换成上述的最优化问题，然后使用枚举搜索的算法找到最优解。最优解对应的一次波是在搜索范围之内具有最大非高斯性的一次波信号，所以这时认为这个时候最优的海面反射系数α和鬼波时延t0将对应最好的一次波。最后用这一对参数逆滤波求出鬼波压制之后的一次波，将得到最好的鬼波压制效果。

2 数值模拟

用参数α=-0.8，t1=8ms来生成鬼波并叠加上一次波信号（见图1a）。其中红色波信号为原始信号，蓝色波信号为包含鬼波信号。从图中可以看出，鬼波对原信号产生了很大的影响。设置参数范围：a ∈(-1.0,-0.6)，t1∈(0.4ms,1.2ms)来搜索。用基于非高斯性最大化的方法，得到估计的参数为：a=-0.72，t1=8ms。然后利用该组估计得到的参数设计逆滤波器来压制鬼波（见图1b）。从图中可以看出压制鬼波后的信号和原信号非常接近。实验结果表明该方法在处理人工合成数据时效果不错。

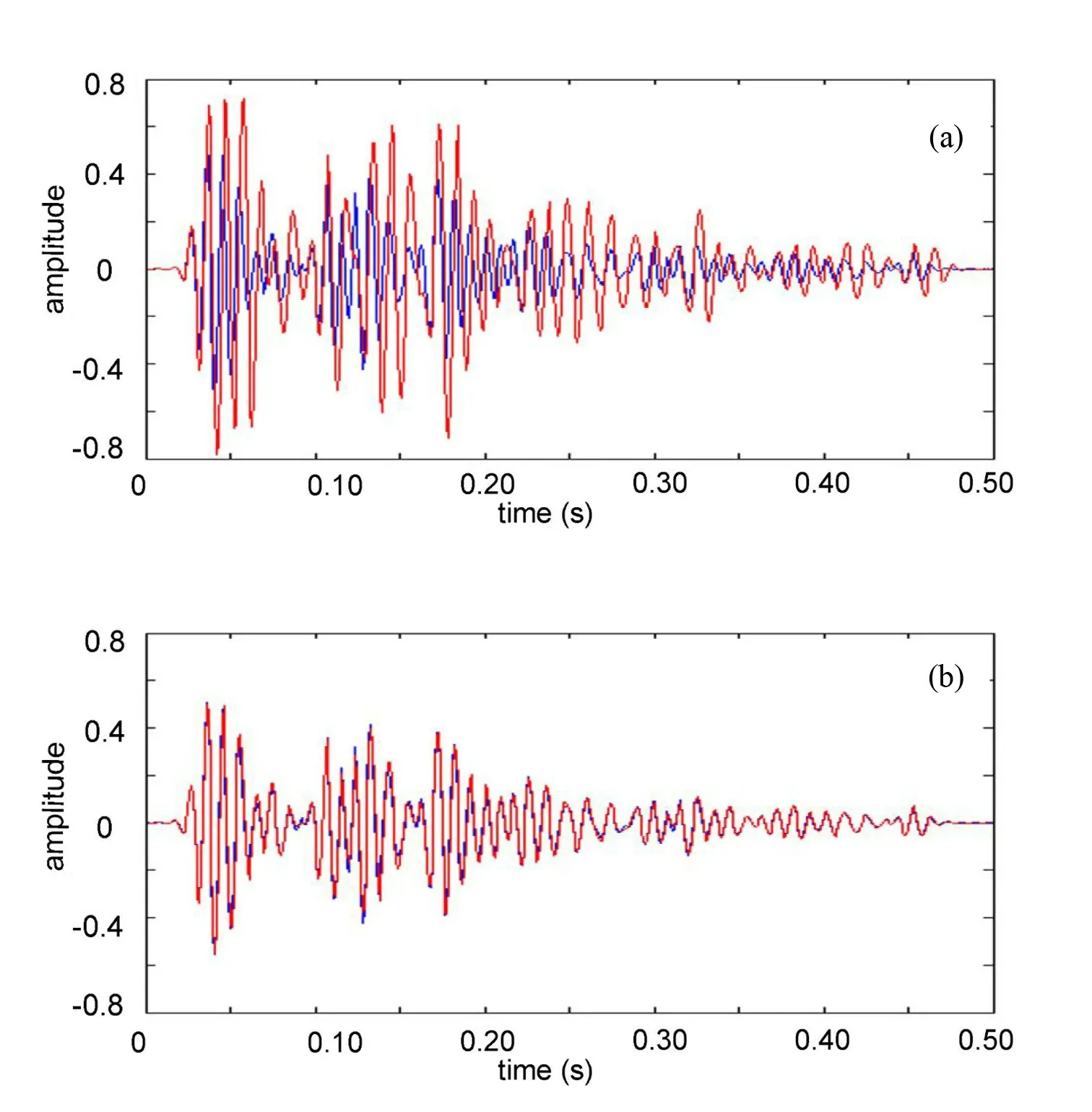
图1 人工合成数据经过该方法压制鬼波前后的时域波形图

3 实际地震资料处理

选用的实际资料是海洋地震数据的一个共炮点道集，有288道，每道有2500个点，采样率为1ms，检波点沉放深度为20m，炮点沉放深度为4m。由于炮点沉放深度非常浅，激发点鬼波第一陷波频率在190Hz 左右，所以在激发点鬼波对整个数据影响不大。本文只考虑压制接收点鬼波。

检波点沉放深度d0=20m,所以接收点鬼波时延的粗略估计值为=26.67ms。由于有地震波入射角的影响，所以实际的鬼波时延肯定要小于这个值。所以本文设定鬼波时延搜索范围为：t0∈(11ms,33ms)，搜索步长t0s=1.1ms。对于海面反射系数本文设定其搜索范围为：α ∈(-0.9,-1)，搜索步长αs=0.01。

本文使用基于非高斯性最大化的鬼波压制的方法逐道去鬼波，然后分析处理前后的频谱。图2 给出的是处理前后所有道的平均振幅谱。从图2中可以看出在低频部分以及30Hz到50Hz范围内陷波点都得到了较好的补偿，补偿的增幅程度平均为25%左右，这表明鬼波被有效的压制。图3 给出的是处理前后f-x 域上的振幅谱，其中图a 为原信号的振幅谱,图b 为压制鬼波后的信号的振幅谱。压制鬼波后，鬼波的振幅减小，目标信号的振幅增强，从F-K 谱上可以观察到频率范围为30～50Hz 的陷波带处信号的振幅对比原始信号更加清晰和明显，信噪比得到了提高。从图4 中可以看出处理后的数据具有更多的有效信息，而且具有更高的分辨率，部分同相轴能够清楚地分开，而且多出来的比较弱的轴也得到了很好的压制。总的来说鬼波得到了较好的压制。

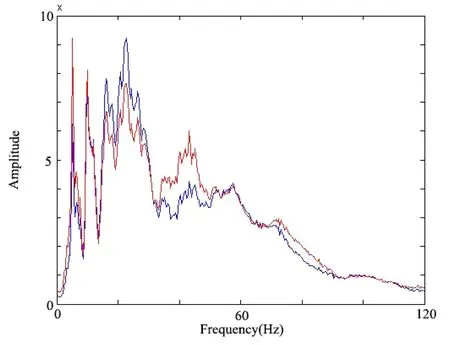
图2 处理前后所有道的平均振幅谱

图3 实际地震资料用该方法压制鬼波前后在f-x域的振幅谱

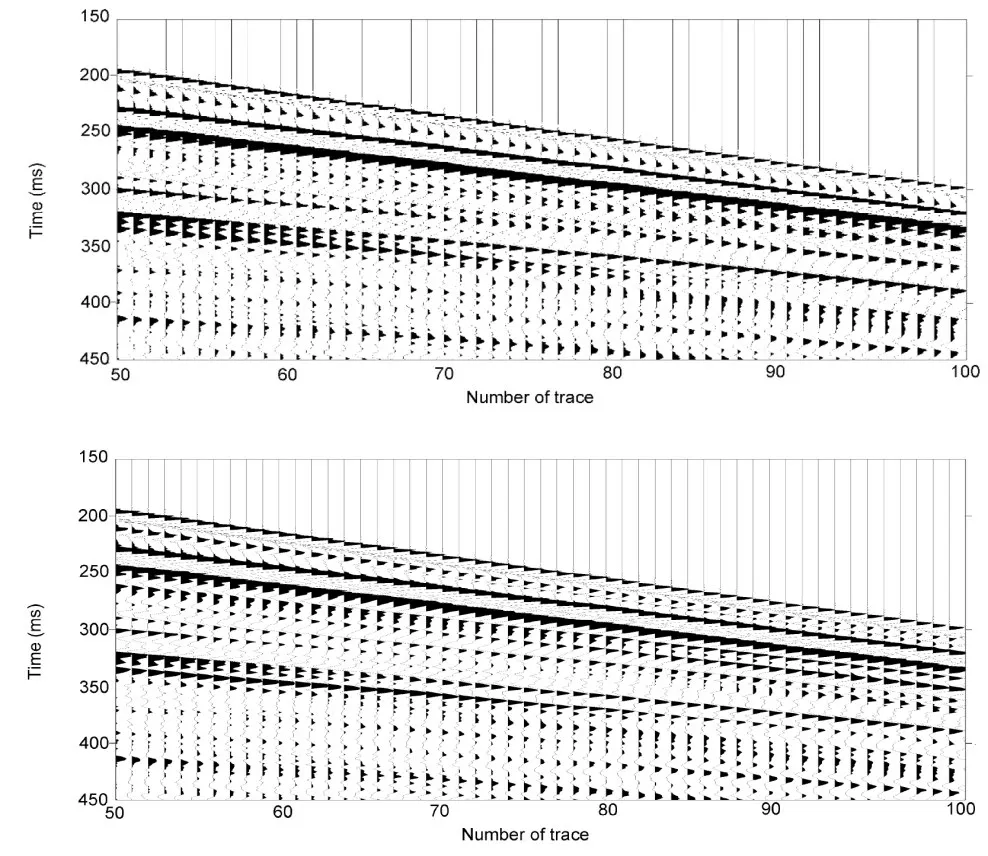
图4 （a）处理前原信号在时域的波形图，（b）用该方法压制鬼波后时域的波形图

对于莺歌海盆地浅水区的地震采集数据，拖缆沉放深度为5m。图5给出了叠前炮集的处理结果（部分放大），图6 为单炮全局效果显示，其中左边是原始数据，中间是压制电缆鬼波后的结果，右边是压制震源鬼波后的结果。由图5 和图6 可得，鬼波紧随在上行波旁边，在炮检距增加时，它们的距离会逐渐扩大，然后再逐渐靠近，而相位则呈相反的趋势。通过本文的优化方法，显著减小了跟随上行波的反相同相轴的鬼波，从而使记录更加清晰，有效信号更加突出。图7给出了鬼波压制前后的频率振幅谱，左边是原始数据的频谱，中间是压制电缆鬼波后的频谱，右边是压制震源鬼波后的频谱。图8给出了近中远单次剖面的鬼波压制前后的频谱对比分析。图9给出了鬼波压制前后的叠加效果对比。由图7～图9 可得，图中体现出了在地震数据上应用鬼波压制前后的频谱和叠加效果对比。可以观察到检波器鬼波在约0～40 和100～140 Hz处产生陷频（红色线），而经过鬼波压制后（蓝色线），这些陷波点被消除。从频谱分析和叠加效果上可以看出，鬼波压制后，有效频带明显拓宽，能量得到有效提升，频谱更为连续。同时在低频陷波点位置得到有效补偿后，低频信号得到了明显的恢复。从数据和相关上也可以直观的看到同向轴更单一，子波压制较干净。因此，通过实际数据处理实验可以得出结论：本文的鬼波压制方法能够有效地抑制鬼波，弥补了由于鬼波存在而导致的频谱缺失，从而提高了地震数据的分辨率。

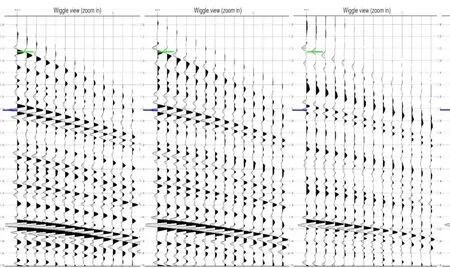
图5 单炮鬼波压制波形对比

图6 单炮鬼波压制

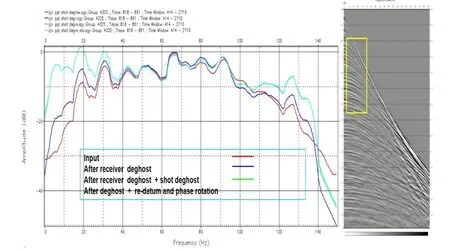
图7 单炮鬼波压制频谱分析

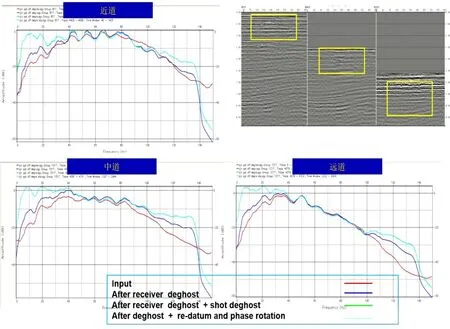
图8 鬼波压制后近中远道频谱对比

图9 鬼波衰减前后剖面对比

4 结论

鬼波是海上地震勘探中不可避免的一种干扰波，鬼波在莺歌海盆地高温高压区的影响非常大，高温高压目的层段受鬼波的影响子波形态改变，频率特征变窄，低频信号被掩盖。本文从几何地震学角度对鬼波的形成机理以及鬼波的种类进行了深入的研究，同时对鬼波的特性以及影响鬼波特性的因素进行了分析和总结，最终从鬼波自身特性出发提出了压制鬼波的方法。鬼波的种类主要有激发鬼波、接收鬼波以及激发和接收鬼波。鬼波在频率域表现为陷波效应，可能对有效频带造成很大的伤害。影响鬼波的因素与影响气泡震荡的因素一样，主要是实际的激发接收条件。在地震记录的频谱特征中可以很明显的看出不同的采集参数鬼波对记录频谱陷频的位置是发生变化的，经过以上研究后，得出结论：

从鬼波的特性出发，论述了非高斯性最大化鬼波压制法的基本原理，给出了非高斯最大化法的具体算法，在模型数据和实际数据中取得了较好的鬼波压制效果。

应用到莺歌海盆地高温高压区地震资料的处理中，水道砂体的顶底界面成像质量改善，中深层低信噪比区，尤其上泥底辟模糊区低频信号恢复明显，有利于后期模糊区内部的速度追踪，为改善成像质量提供了保障。