三种升温模式下钢构件火灾危险性分析
2023-11-28张佳庆黄玉彪蒋恭华何灵欣丁彦铭
张佳庆,黄玉彪,蒋恭华,何灵欣,丁彦铭*
(1.国网安徽省电力有限公司电力科学研究院电力火灾与安全防护安徽省重点实验室(国家电网公司输变电设施火灾防护实验室),安徽 合肥 230601;2.中国地质大学(武汉)工程学院,湖北 武汉 430074)
火灾是变电站的重要安全隐患之一,变电站建筑采用的钢材虽是不燃材料,但钢材的导热系数较大,其在火灾情况下升温较快,弹性模量和屈服强度等受高温影响也非常显著[1-3]。当温度高于250 ℃时,钢材的弹性模量和屈服强度开始减小,当温度升到400 ℃时,其屈服强度减小到常温时的1/2,当温度升到600 ℃时,其屈服强度降低到室温时的10%[4]。伴随着钢材在高温环境下的受热膨胀作用,其内部会产生附加应力与变形,导致钢结构的稳定性被破坏[5-7]。
变电站作为一个特殊场所,其除了可能发生常见的标准火灾外,还可能发生由电力设备如电缆、电线等引起的电力火灾,同时其内部储存的大量变压器油易在变压器故障、高温情况下发生泄漏并燃烧,出现更为严重的碳氢火灾[8-9]。因此,在变电站火灾中,标准火灾、电力火灾和碳氢火灾三种火灾隐患同时存在,这三种火灾升温曲线的数学表达式[10]分别为
T=345lg(8t+1)+T0
(1)
T=1 030(1-0.325e-0.167t-0.675e-2.5t)+T0
(2)
T=1 080(1-0.325e-0.167t-0.675e-2.5t)+T0
(3)
式中:T表示对应于相关时间t的升温温度(℃);T0为实验开始前的环境温度(℃);t为测试开始时的时间(min)。
目前,有关钢结构在火灾下的抗火性能,国内外学者已开展了相关研究,但现有研究大多采用标准火灾升温曲线对钢结构进行实验及数值模拟分析[11]。如:胡鹰等[12]在既有一榀框架受火实验的基础上建立了该实验框架的有限元模型,通过模拟结果与实验结果的对比,获得了较好的温度场模拟结果;Tondini等[13]对高强度钢进行标准火灾升温下的实验,并通过ABAQUS建立了有限元模型,发现模拟结果与实测数据之间具有良好的一致性;王银志等[14]利用ANSYS有限元软件对有端部约束的钢梁进行了抗火性能数值模拟分析,验证了有限元分析的可靠性;汪洋等[15]基于ANSYS研究了钢框架受火后的温度场,得出当钢框架单跨房间受火时,需要在20 min内采取措施以控制火情;Shnal等[16]通过数学模型模拟火灾温度状态对钢结构机械特性的影响,发现随着火灾荷载密度的增加,钢结构的实际耐火极限逐渐降低。
然而,电力火灾、碳氢火灾升温模式下钢构件的温升变化规律还未见研究报道,特别是三种火灾升温模式下钢构件的温升变化对比也尚不明确。此外,无防火保护(防火涂层脱落)的钢构件遭遇火灾时,其厚度和荷载比对其升温有重要的影响。因此,本文根据《建筑构件耐火试验 可供选择和附加的试验程序》(GB/T 26784—2011)[10],研究三种升温模式、钢板厚度及荷载比对钢构件温升的影响。因钢构件温度升到550 ℃左右时,其力学性能下降十分明显,结构已被破坏,此外,为方便后续研究中与有防火保护的钢构件的耐火极限进行对比,本文取《钢结构防火涂料》(GB 14907—2018)[17]规定的538 ℃作为不同厚度钢板的临界温度值。施加不同荷载后钢构件的对应临界温度根据《建筑钢结构防火技术规范》(GB 51249—2017)[18]确定。
本文首先使用自制的耐火实验炉对三种火灾升温模式下不同厚度钢板背火面温度随时间的变化进行了实验研究;接着,采用ABAQUS软件对以上实验结果进行模拟复现,以验证模拟结果的准确性和有效性[19-20];最后,对三种火灾升温模式下钢构件达到临界温度时间与钢构件荷载比的关系进行了数值模拟。
1 实验概况
1.1 实验样品制备
本文所用钢构件基材为Q235钢,选取尺寸分别为200 mm×150 mm×2 mm、200 mm×150 mm×4 mm和200 mm×150 mm×8 mm(长×宽×厚)的钢板,厚度d为实验变量。首先用砂纸将钢板表面打磨干净,再用无水乙醇等有机溶剂擦去钢板表面的杂质。
1.2 实验过程
实验采用自制的可温度编程的耐火实验炉(图1),其炉体采用陶瓷纤维炉膛,可实现快速升温以满足三种火灾升温模式的要求。
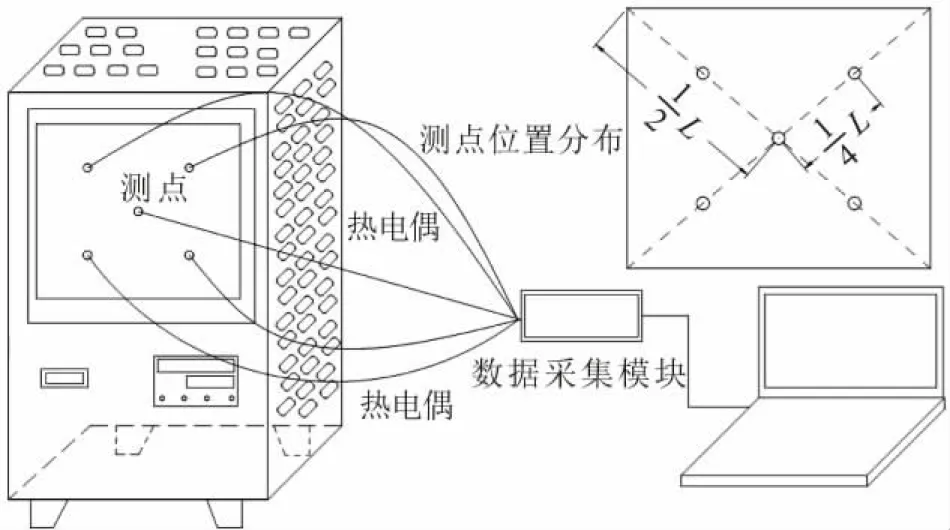
图1 耐火实验装置Fig.1 Test device of fire resistance
升温程序参照标准火灾、电力火灾和碳氢火灾的升温曲线,升温时间设置为60 min。采用简易支架和耐高温胶布固定5个K型热电偶,保证热电偶测温端与钢板背火面紧密接触,固定点在钢板背火面对角线距离(L)的1/2处和1/4处,测点位置如图1所示。当5个测点的钢板背火面平均温度达到538 ℃时判定钢板力学性能失效,测点温度取三次重复性实验的平均值,将实验时间记录为钢板力学性能遭到破坏的时间。
2 结果与讨论
2.1 不同厚度钢板温升实验结果与分析
三种火灾升温模式下不同厚度钢板背火面温度随时间的变化曲线如图2所示。
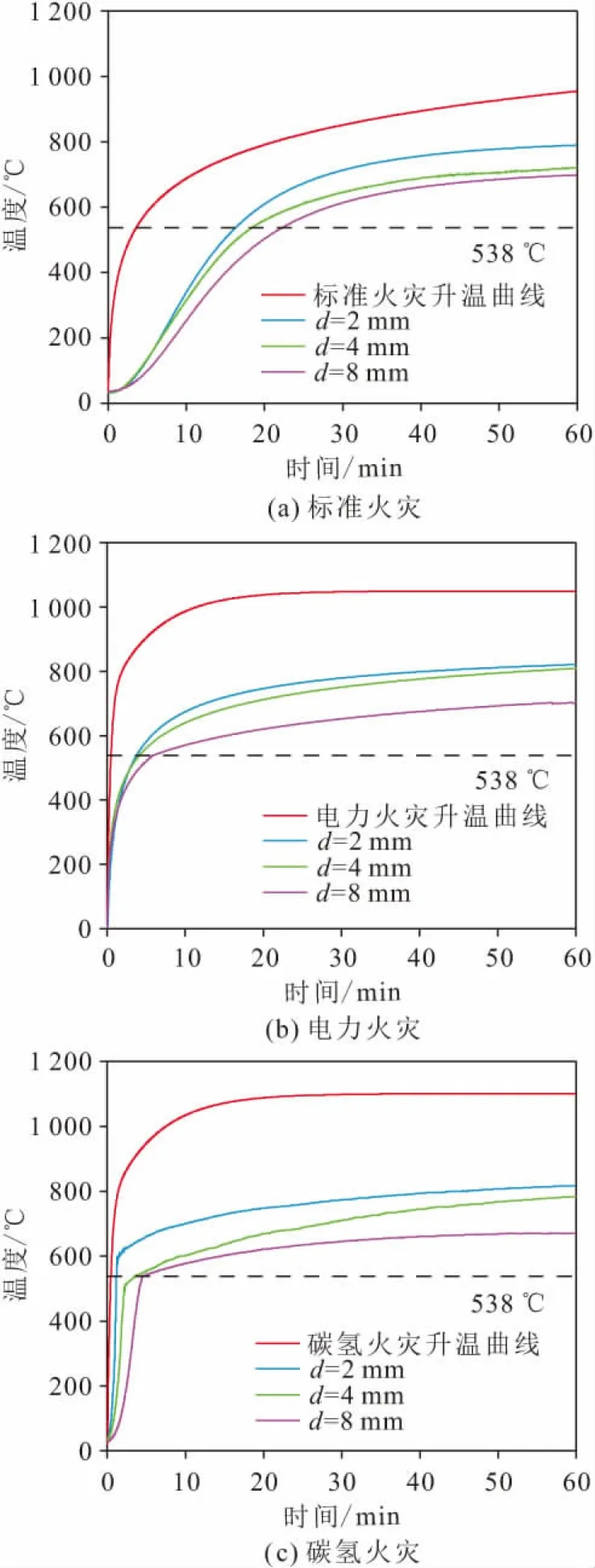
图2 三种火灾升温模式下不同厚度钢板背火面温度随 时间的变化曲线Fig.2 Variation curves of backfire surface temperatures of steel plates of different thicknesses with time in three fire heating modes
由图2可知:
1) 标准火灾升温模式下,火灾发生11 min后,三种厚度钢板背火面温度都超过了300 ℃,平均升温速率达27 ℃/min;当火灾发生16.2、18.5、22.1 min时,厚度为2、4、8 mm钢板的背火面平均温度分别达到了538 ℃,钢板厚度增加一倍,其达到临界温度的时间增加了14%~20%;当火灾发生22.1 min后,钢板背火面最高温度超过538 ℃,平均升温速率达25 ℃/min,此时钢板已经丧失大部分弹性模量和屈服强度[图2(a)]。
2) 电力火灾升温模式下,火灾发生2 min后,三种厚度钢板背火面温度都超过400 ℃,平均升温速率达200 ℃/min;当火灾发生2.5、3.8和5.9 min时,厚度为2、4和8 mm钢板的背火面平均温度分别达到538 ℃,钢板厚度增加一倍,其达到临界温度的时间增加了52%~55%;当火灾发生6 min后,钢板背火面最高温度超过538 ℃,平均升温速率达90 ℃/min,即电力火灾下的升温速率是标准火灾升温模式下的7.4倍[图2(b)]。
3) 碳氢火灾升温模式下,火灾发生2 min后,三种厚度钢板背火面温度均超过450 ℃,平均升温速率达225 ℃/min;当火灾发生2.2、3.4和5.1 min时,厚度为2、4和8 mm钢板的背火面平均温度均达到538 ℃,钢板厚度增加一倍,其达到临界温度的时间增加了50%~55%;当火灾发生5.1 min后,钢板背火面最高温度均超过538 ℃,平均升温速率达107.6 ℃/min,即碳氢火灾升温模式下钢板背火面的升温速率是三种火灾升温模式中最大的,而更快的升温速率会导致钢板的力学性能急剧下降,对钢结构的稳定性造成破坏[图2(c)]。
通过上述分析可知,电力火灾和碳氢火灾相对标准火灾而言,钢板厚度对其温升速率的影响更大。
2.2 不同火灾升温模式下钢板温升实验结果与分析
厚度为2 mm的钢板在三种火灾升温模式下的背火面温度变化曲线,如图3所示。
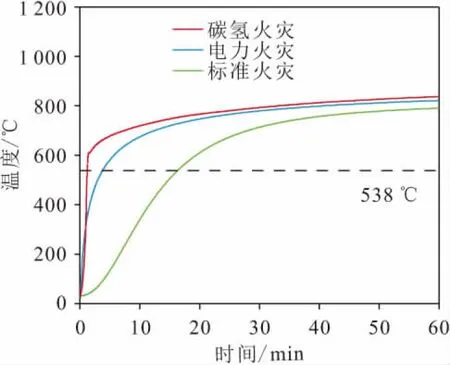
图3 三种火灾升温模式下厚度为2 mm的钢板背火 面温度随时间的变化曲线Fig.3 Variation curves of backfire surface temperature of steel plates of 2 mm thickness with time in three fire heating modes
由图3可知:电力火灾和碳氢火灾升温模式下钢板背火面温度在前期升温迅速,在达到600 ℃后升温速率逐渐变缓;标准火灾模式下钢板达到临界温度值(538 ℃)的时间为16.2 min,而电力火灾模式下对应的时间为2.5 min,相比于标准火灾模式时间缩短了84.6%;在碳氢火灾模式下钢板达到临界温度值的时间为2.2 min,相比于标准火灾模式时间缩短了86.3%。
三种火灾升温模式下不同厚度钢板达到临界温度(538 ℃)时间的实验结果见表1。
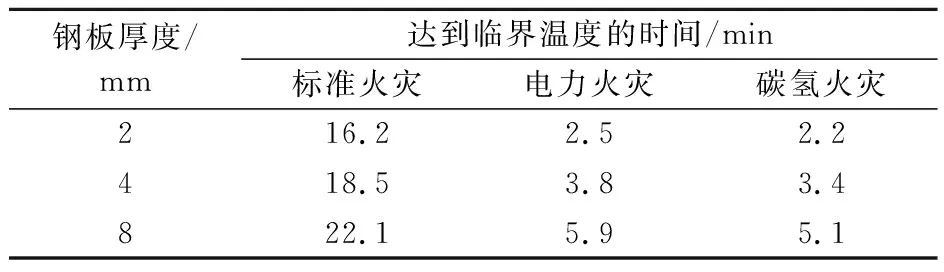
表1 三种火灾升温模式下不同厚度钢板达到临界温度时间的实验结果
由表1可知:在标准火灾升温模式下厚度为4 mm的钢板达到临界温度(538 ℃)的时间为18.5 min,而电力火灾升温模式下对应的时间为3.8 min,相比于标准火灾升温模式时间缩短了79.5%;在碳氢火灾升温模式下厚度为4 mm的钢板达到临界温度的时间为3.4 min,相比于标准火灾升温模式时间缩短了81.6%。电力火灾和碳氢火灾与标准火灾相比,钢板达到临界温度的时间急剧缩短,缩短幅度达到70%以上,最高达到了86.3%,这主要是由于电力火灾和碳氢火灾前期升温速率较高,这也是其与标准火灾之间最明显的区别。由此可见,在变电站环境中,无防火保护或者防火涂料脱落的钢构件在遭遇火灾时是十分不安全的。
2.3 数值模拟实验工况设置及数值模拟结果验证
本文利用有限元分析软件ABAQUS建立上述实验钢构件的有限元模型,采用不同的火灾升温曲线加载模拟不同火灾升温模式下钢构件温度随时间的变化。火灾发生时影响钢构件升温的主要因素有钢材的热传导系数、比热容和密度[21]。其中,热传导系数是指在升高单位温度条件下,单位面积上单位时间内所传递的热量[W/(m·℃)或W/(m·K)][12],本文中钢材的热传导系数取值如图4所示;比热容是单位质量物体改变单位温度时吸收或释放的内能[J/(kg·℃)或J/(kg·K)[12]],本文中钢材的比热容按欧洲规范EC3的相关规定进行取值,如图4所示;钢材的密度ρs在火灾发展的温度范围内变化很小,其值基本保持恒定,在钢结构抗火分析过程中一般取为常数7 850 kg/m3[12]。
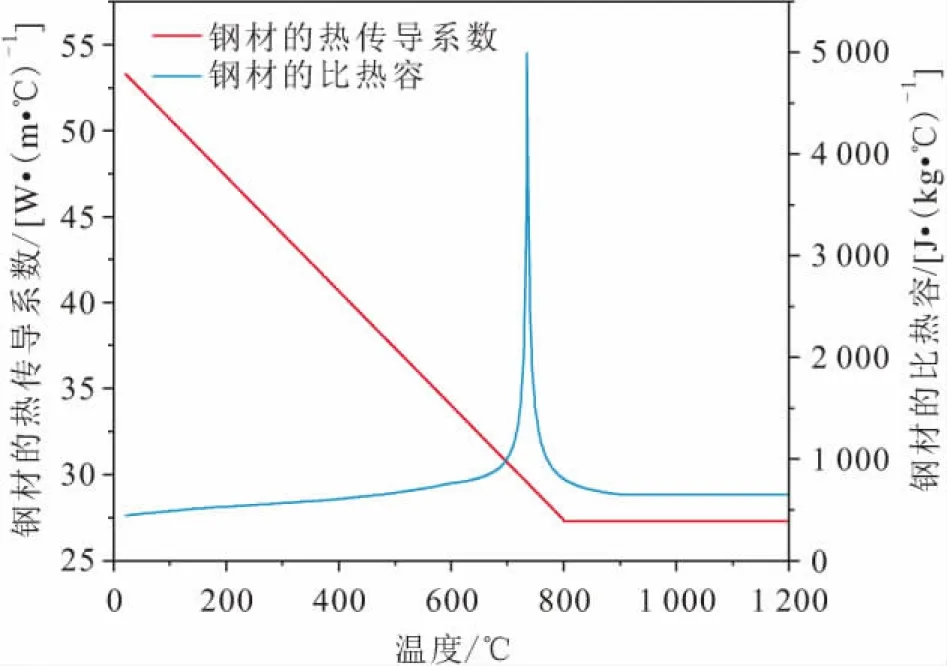
图4 钢材的热物理参数Fig.4 Thermal physical parameters of steel
本文采用瞬态非线性传热分析方法,对火炉内热量通过热对流和热辐射传递给钢构件进行分析。热辐射系数是衡量物体表面接近理想黑体程度的指标,其取值因火炉不同而略有差异,本文取0.7;对流换热系数参照欧洲规范EN 1991-1-2的规定,取25 W/(m2·K)。有限元模型全部使用三维实体单元,单元类型为DC3D8[21]。三种火灾升温程序在幅值表中设定,火灾升温时间为60 min。
三种火灾升温模式下不同厚度钢板背火面温度达到临界温度(538 ℃)的时间的数值模拟结果与实验结果的对比,如图5所示。
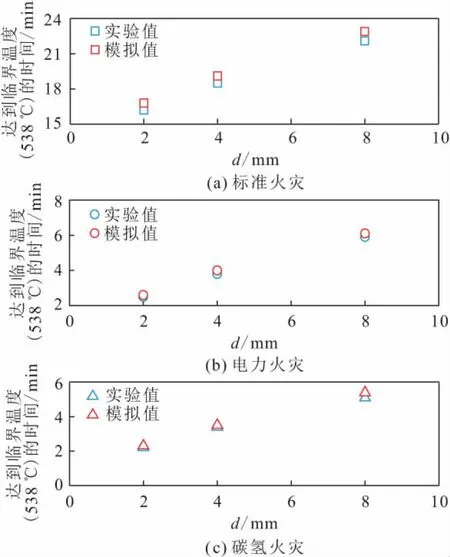
图5 数值模拟结果与实验结果的对比Fig.5 Comparison between numerical simulation results and experimental results
由图5可知:在标准火灾升温模式下,厚度为2、4、8 mm钢板达到临界温度的时间的数值模拟结果与实验结果的误差为3.57%、3.14%、3.49%;在电力火灾升温模式下,厚度为2、4、8 mm钢板达到临界温度的时间的数值模拟结果与实验结果的误差为3.85%、5%、3.28%;在碳氢火灾升温模式下厚度为2、4、8 mm钢板达到临界温度的时间的数值模拟结果与实验结果的误差为4.35%、2.86%、3.77%。由此说明钢板达到临界温度的时间的数值模拟结果与实验值吻合良好,具有较高的精度,且偏差均小于5%。因此,本文可采用ABAQUS软件对钢构件达到临界温度的时间进行模拟复现,从而可用于进一步分析更复杂钢构件在火灾升温中达到临界温度的时间的变化规律。
2.4 局部钢构件达到临界温度的时间与荷载比的关系分析
钢梁是钢结构中的重要受力构件,不同荷载状态的钢梁遭遇高温时可承受的极限温度不同[22]。为研究荷载比对钢梁达到临界温度时间的影响,选取截面尺寸为390 mm×300 mm×10 mm的H型钢梁,三面受火条件下其截面形状系数为125 m-1,四面受火条件下其截面形状系数为147 m-1。本文采用ABAQUS软件对不同火灾升温模式下荷载比为0.50、0.55、0.60、0.65、0.70的钢梁达到临界温度的时间进行数值模拟分析。根据《建筑钢结构防火技术规范》(GB 51249—2017),不同荷载比钢梁对应的临界温度确定为581、562、542、523、502 ℃[17]。
三面受火钢梁在不同荷载比下达到临界温度的时间的变化曲线,如图6所示。
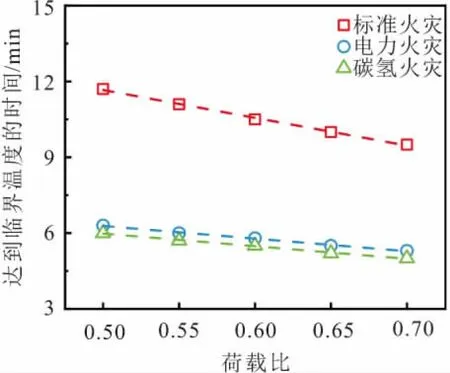
图6 三面受火钢梁在不同荷载比下达到临界温度的 时间的变化曲线Fig.6 Curves of time to critical temperature for steel members subjected to fire on three sides at different load ratios
由图6可知:钢梁达到临界温度的时间随钢梁荷载比的增大呈线性减小趋势;钢梁荷载比大于0.70时,其在三种火灾升温模式下达到临界温度的时间均低于10 min,钢梁稳定性失效的危险性较大;荷载比为0.60的钢梁在电力火灾和碳氢火灾升温模式下达到临界温度的时间均低于6 min,远小于标准火灾升温模式下的10.6 min,降幅超过40%。
通过对三种火灾升温模式下三面受火钢梁荷载比与其达到临界温度的时间的拟合,可得到以下关系式:
y=-11x+17.2 (R2=0.99)(标准火灾)
(4)
y=-5x+8.8 (R2=0.99)(电力火灾)
(5)
y=-5x+8.5 (R2=0.99)(碳氢火灾)
(6)
上式中:y为钢梁达到临界温度的时间(min);x为钢梁的荷载比。
在同一火灾升温模式下,钢梁的荷载比越大,其达到临界温度的时间越短。
同理,四面受火钢梁在不同荷载比下达到临界温度的时间的变化曲线,如图7所示。
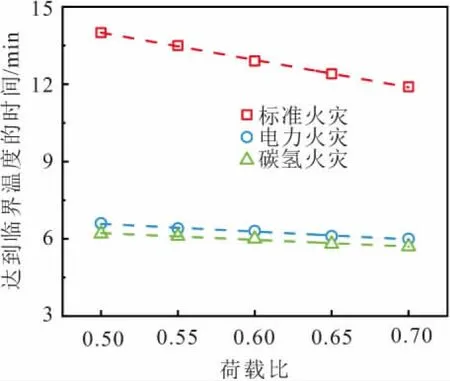
图7 四面受火钢梁在不同荷载比下达到临界温度的 时间的变化曲线Fig.7 Curves of the time to critical temperature for steel members subjected to fire on all sides at different load ratios
由图6、图7可知,与三面受火钢梁相比,四面受火钢梁在电力火灾、碳氢火灾升温模式下达到临界温度的时间平均下降44.62%,表明四面受火钢梁的荷载比对其到达临界温度的时间的影响更大。
通过对三种火灾升温模式下四面受火钢梁荷载比与其达到临界温度的时间的拟合,可得到以下关系式:
y=-10.6x+16.3 (R2=0.99)(标准火灾)
(7)
y=-3x+5.1 (R2=0.99)(电力火灾)
(8)
y=-2.6x+4.5 (R2=0.98)(碳氢火灾)
(9)
上式中:y为钢梁达到临界温度的时间(min);x为钢梁的荷载比。
3 结 论
1) 实验钢构件在标准火灾升温模式下达到临界温度的时间范围为16~23 min,电力火灾、碳氢火灾升温模式下其达到临界温度的时间为2~6 min;电力火灾和碳氢火灾升温模式下钢构件达到临界温度的时间相对标准火灾升温模式急剧缩短,平均缩短幅度超60%,最大幅度达86.3%。
2) 电力火灾、碳氢火灾中钢梁荷载比大于0.70时,达到临界温度的时间均低于6 min,钢梁稳定性失效的危险性较大。
3) 局部钢构件——钢梁达到临界温度的时间与荷载比呈线性关系,并得到了三面受火、四面受火钢梁在三种火灾升温模式下达到临界温度的时间与其荷载比的拟合方程。
