新四维耗散非线性系统动力学行为分析及电路设计
2023-11-28瞿民凯赵思远黄驿婷罗芳文
瞿民凯,汤 琼,赵思远,黄驿婷,罗芳文
(湖南工业大学 理学院,湖南 株洲 412007)
1 研究背景
混沌是一种貌似无规则的运动,指在确定性非线性系统中,不需要附加任何随机因素亦可出现类似随机的行为。它体现了确定性与不确定性、有序性与无序性、规则性与无规则性的有机统一[1-2]。
20世纪初期,法国科学家庞加莱在研究著名的“三体问题”时发现[3],对于参数固定的三阶常微分方程组,即使初始条件存在很小的差别,最终所呈现的解的形态可能完全不同,学者们把这一现象称为“蝴蝶效应”,这是混沌研究的原形。后来的几十年中,对混沌学者们展开了更深入的研究。
真正拉开混沌方面研究序幕的是混沌之父E.N.Lorenz。非线性系统理论是数学和物理学的一个重要分支,自洛伦兹发现了混沌现象以来[4],它在很多领域都有着广泛的应用[5]。许多非线性系统同步和控制方法的提出[6-11],加快了混沌学的发展,并使其逐渐趋于成熟[12]。
20世纪八九十年代,混沌与其它学科相互促进发展,特别是在密码学、神经网络、经济学等领域有了较大的进展[13-14]。这些研究加快了混沌理论在工程实际中应用的脚步,推动了混沌应用的发展。在工程领域中,随着某个参数的变化,非线性系统若能在更宽的范围内一直维持混沌状态,其在保密通信[15]、密码学、混沌控制等领域中,会更有优势。
在混沌理论建立的过程中,Q.Rossler 于1979年突破了高维系统中存在超混沌的研究,在仅有一个非线性项的四维系统中发现了超混沌吸引子,即超混沌Rossler 系统。此后,学者们通过一系列的方法构建并研究超混沌系统,D.Cafagna 等[16]采用耦合三维Chua 电路得到高维超混沌Chua 电路。Chua电路属于经典的混沌系统,对它的研究具有非常重要的价值。2009年Yang Q.G.等[17]在三维Yang 系统中应用反馈控制器,得到具有唯一平衡点的四维超混沌系统。2012年Sun K.等[18]在Lorenz 型系统的基础上,得到了一个三维非自治的超混沌系统。2015年Chen Y.M.等[19]发现平衡点曲线与超混沌吸引子共存的四维超混沌系统。2017年Li X.Y.等[20]发现了具有无穷多奇异退化异宿环的四翼超混沌系统。2018年Chen Y.M.[21]发现具有4 种不同类型吸引子共存的四维Lorenz-like 多重稳定性的超混沌系统。
目前,破译者们已将较为经典的超混沌系统,研究的相当透彻,这使其在保密通信和混沌信息加密中的安全性大大降低,故新的超混沌系统的设计、实现是当今国内外研究的热点。
和混沌系统相比,超混沌系统具有更加丰富的动力学特性,从而使其在密码学和信息安全等领域有着独特的优越性。通过设计新型的超混沌系统,深入了解其原理,并在理论上研究其应用,才能在未来利用超混沌和抑制超混沌。随着混沌理论的不断发展,人们对于混沌和超混沌的研究不再仅仅局限于理论分析和数值仿真,还可以通过电路来实现混沌系统,并产生相应的混沌信号,因而其信号处理领域具有广阔的应用前景。
本文通过非线性反馈控制,构造了一个新的四维超混沌系统。对该系统平衡点类别及稳定性进行了分析,运用相图、分岔图、Lyapunov 指数谱、庞加莱截面图等方法研究了系统的动力学行为,系统随新引入的参数变化表现出非常丰富的动力学行为,呈现出超混沌、混沌、周期状态。另将有限元方法和Runge-Kutta 方法所求得的,该系统的数值解进行了对比。并设计了该系统的模拟电路,验证了该系统的可实现性,为非线性系统分析提供好的思路。
2 新型超混沌系统
文献[22]中三维混沌系统的数学模型为
式中参数a、b、c均大于0。
当参数a=8、b=2.5、c=1时,系统会处于混沌状态。基于上述系统(1),本文通过增加非线性反馈控制器构造了一个新的四维超混沌系统,如式(2)所示:
式(2)中:w为新引入的状态变量;d和e均为引入的系统参数。
通过大量的数值实验发现,当a=10、b=4、c=5、d=4、e=1,4 个系统变量初值为[1,1,1,1]时,系统会呈现出超混沌状态,产生超混沌吸引子。下面针对本文所提出的新四维超混沌系统进行动力学行为分析。
3 系统的动力学行为分析
3.1 耗散性与吸引子存在性
3.2 平衡点稳定性分析
将a=10、b=4、c=5、d=4、e=1,代入方程组(3),通过计算可求得该系统唯一的平衡点为P(0,0,5,0),在平衡点P处的Jacobian 矩阵为
当a=10、b=4、c=5、d=4、e=1 时, 令λE-J的行列式为0,求得矩阵J的特征值分别为λ1=-16.031 4,λ2=12.285 3,λ3=-0.253 9,λ4=-1.000 0,即λ1、λ3、λ4的实部<0,λ2的实部>0,根据Routh-Hurwitz 判据可知,P是不稳定的平衡点。
3.3 参数变化对系统运动状态的影响
混沌系统中参数对系统运动状态的影响,可通过该参数变化下系统的Lyapunov 指数谱和分岔图产生的变化规律来进行刻画。观察系统(2)随各参数变化的Lyapunov 指数谱,发现系统(2)在参数e取不同值时,会呈现周期、混沌及超混沌等丰富的动力学行为。图1 是本文提出的新型超混沌系统随参数e变化的Lyapunov 指数谱和分岔图,参数e的取值范围为[0,40]。
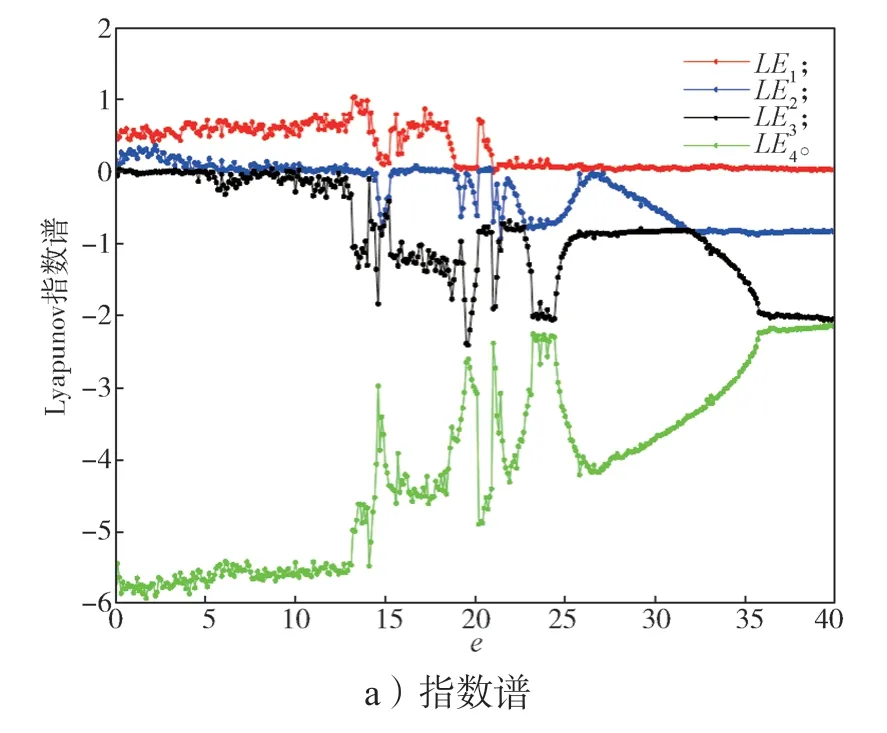
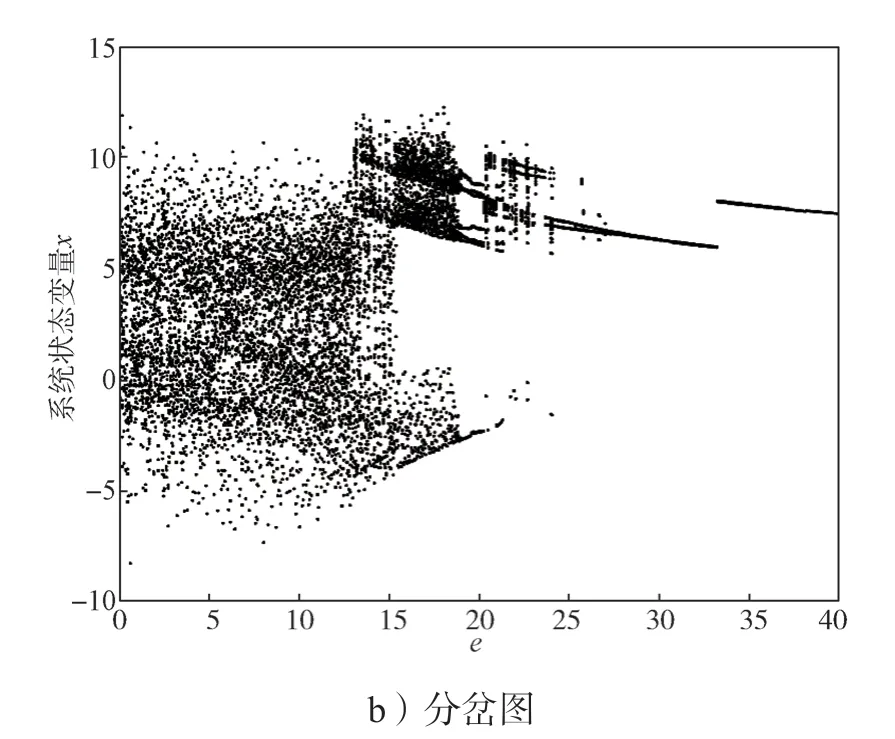
图1 新型超混沌系统Lyapunov 指数谱和分岔图Fig.1 Lyapunov exponential spectrum and bifurcation diagram of a novel hyperchaotic system
由图1,当a=10、b=4、c=5、d=4,系统变量初值为[1,1,1,1]时,系统(2)随参数e变化的Lyapunov 指数谱和分岔图可知,新型超混沌系统在参数的变化下所呈现的运动状态如下。
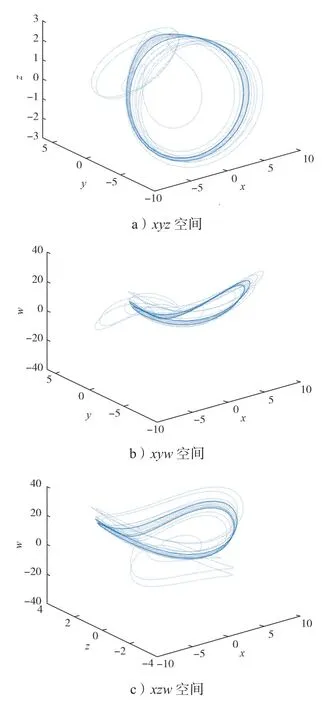
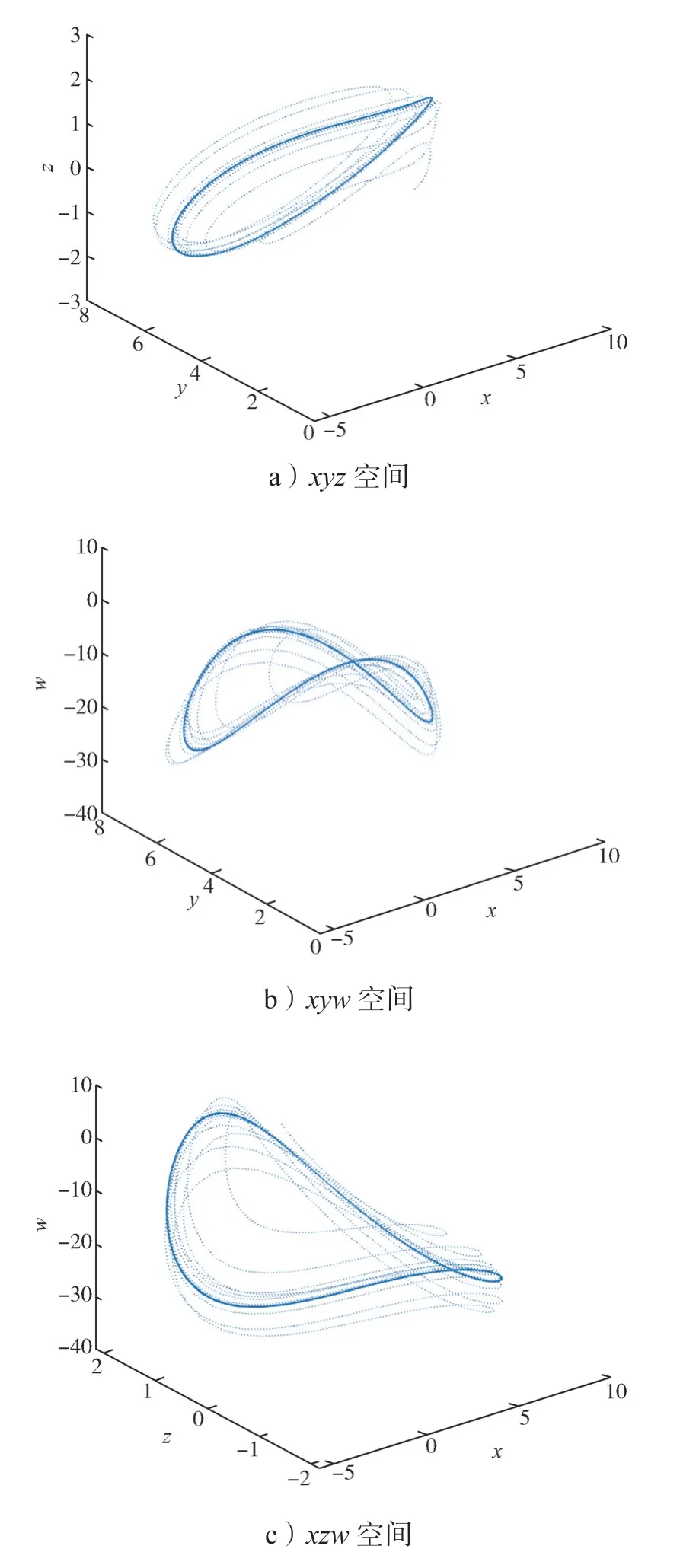
1) 当0
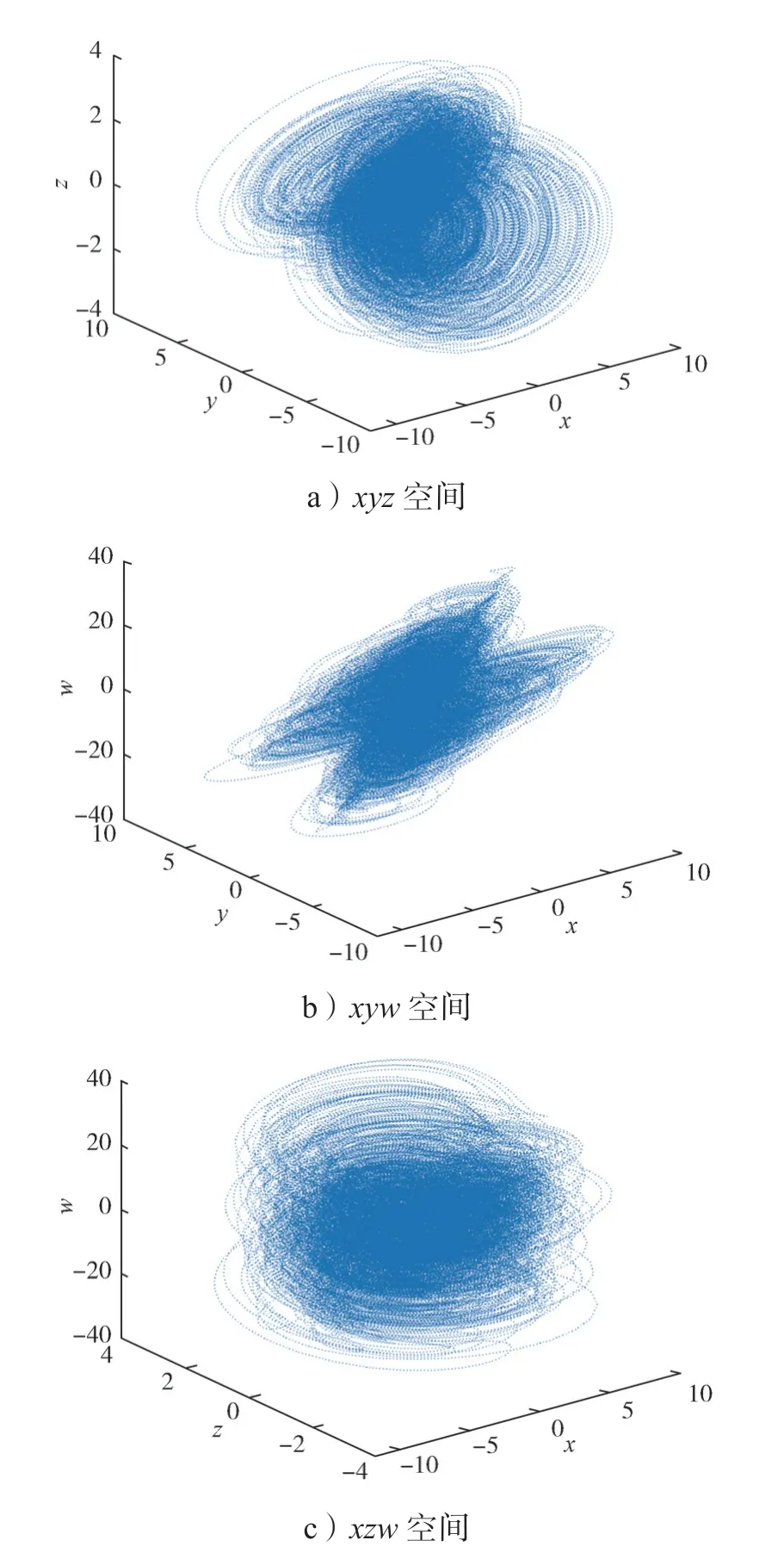
图2 e=1 时系统在三维空间中的相图Fig.2 Phase diagram of the system in three-dimensional space with e=1
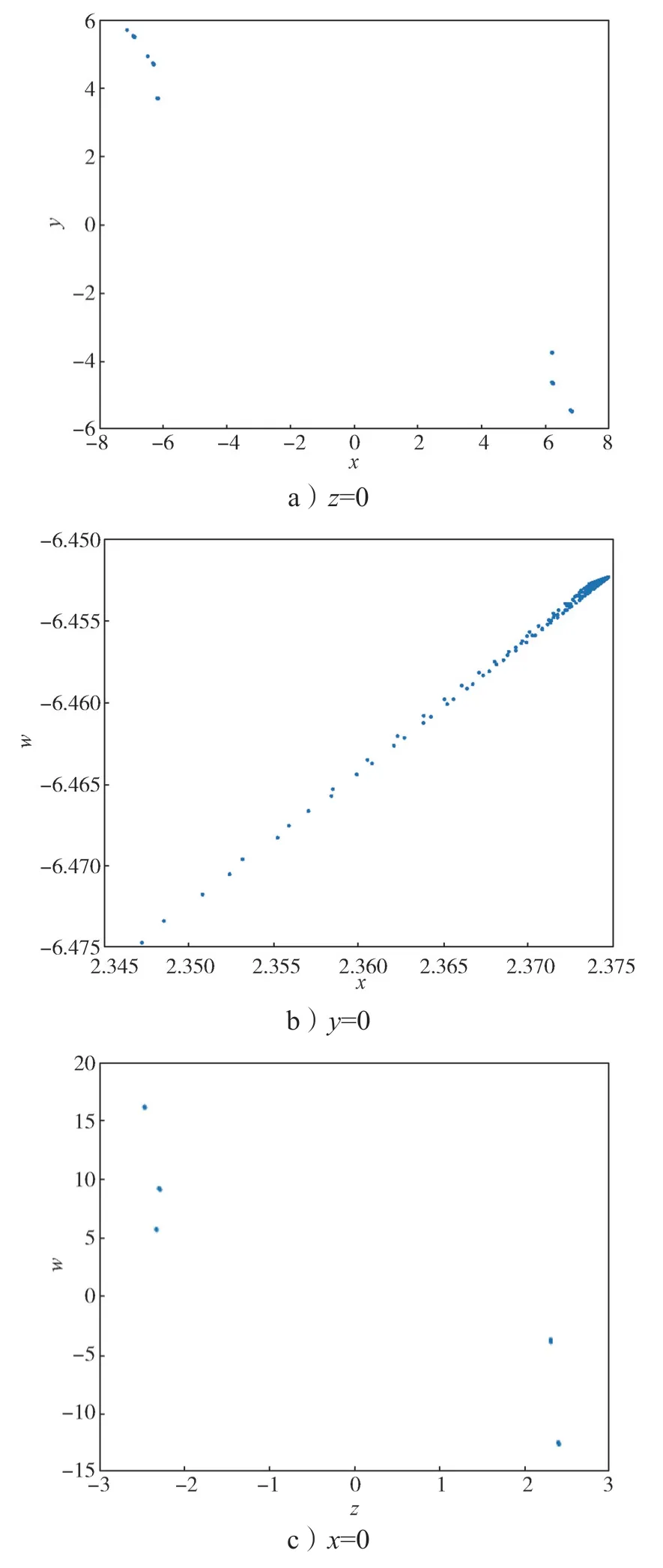
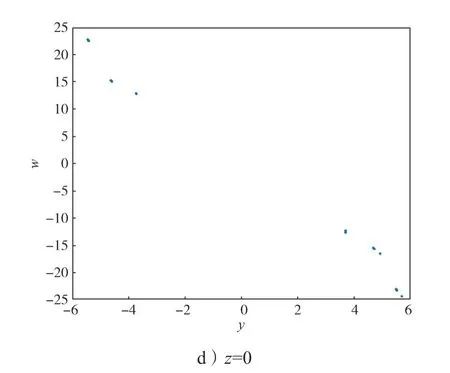
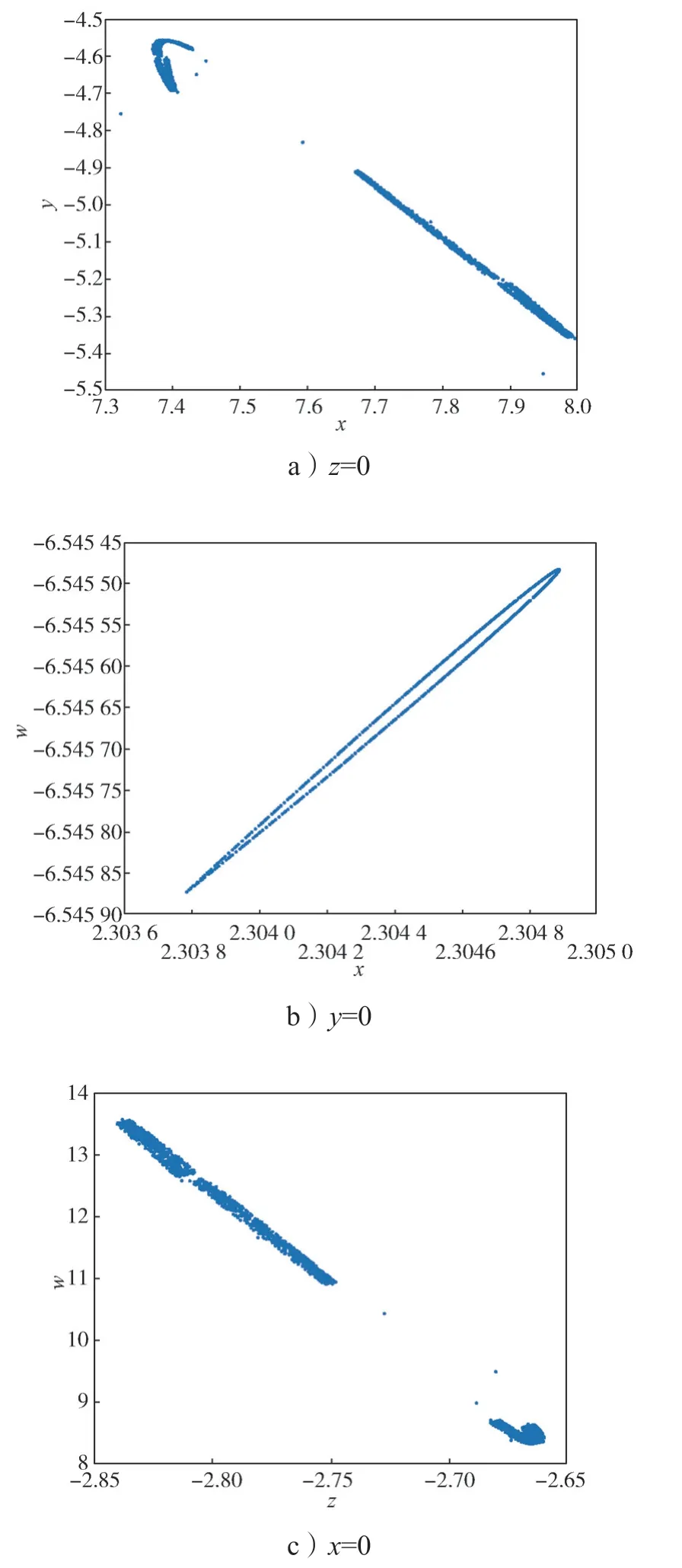
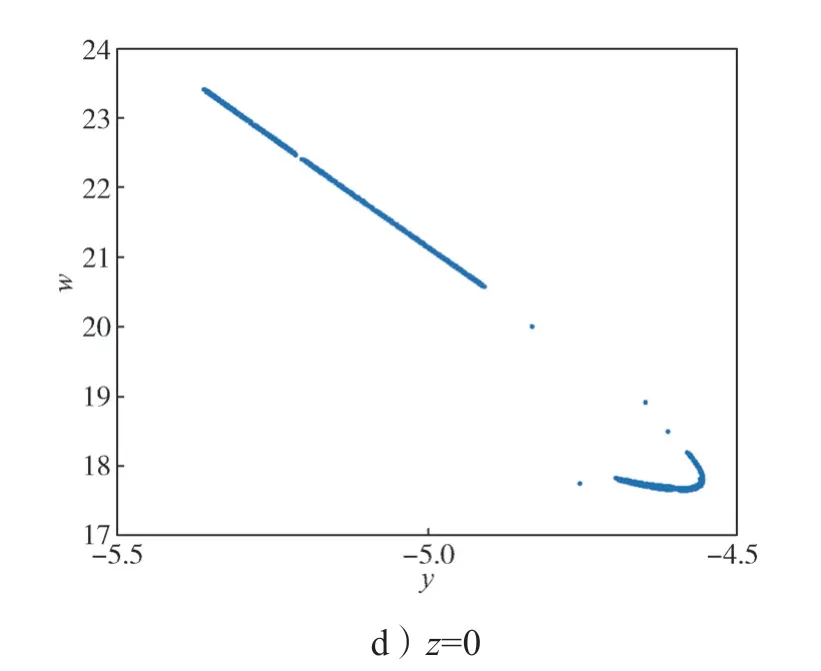
此时系统(2)的庞加莱截面图如图3所示。
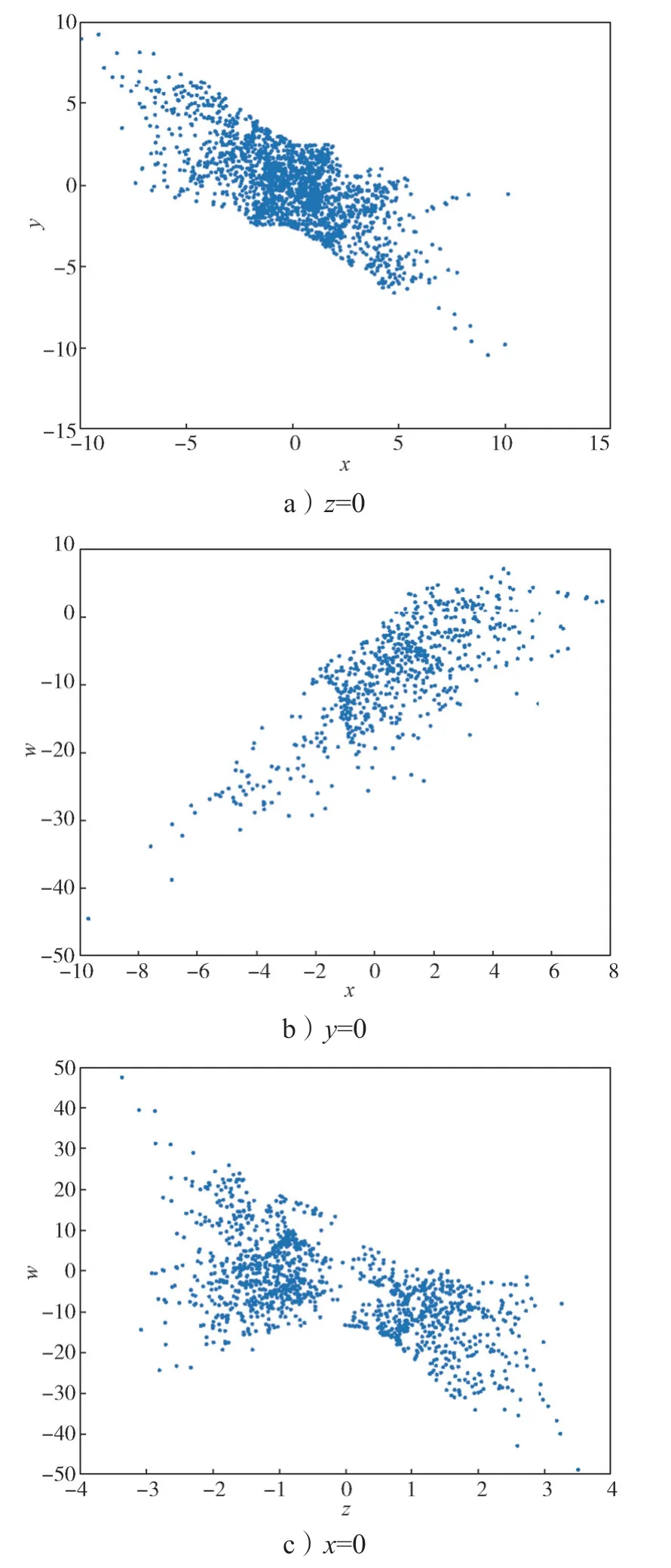
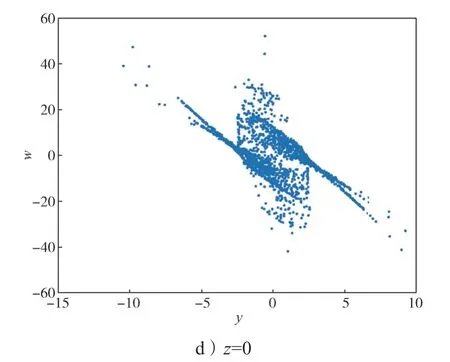
图3 e=1 时系统的庞加莱截面图Fig.3 Cross-section of the system Poincaré with e=1
2) 当4.2
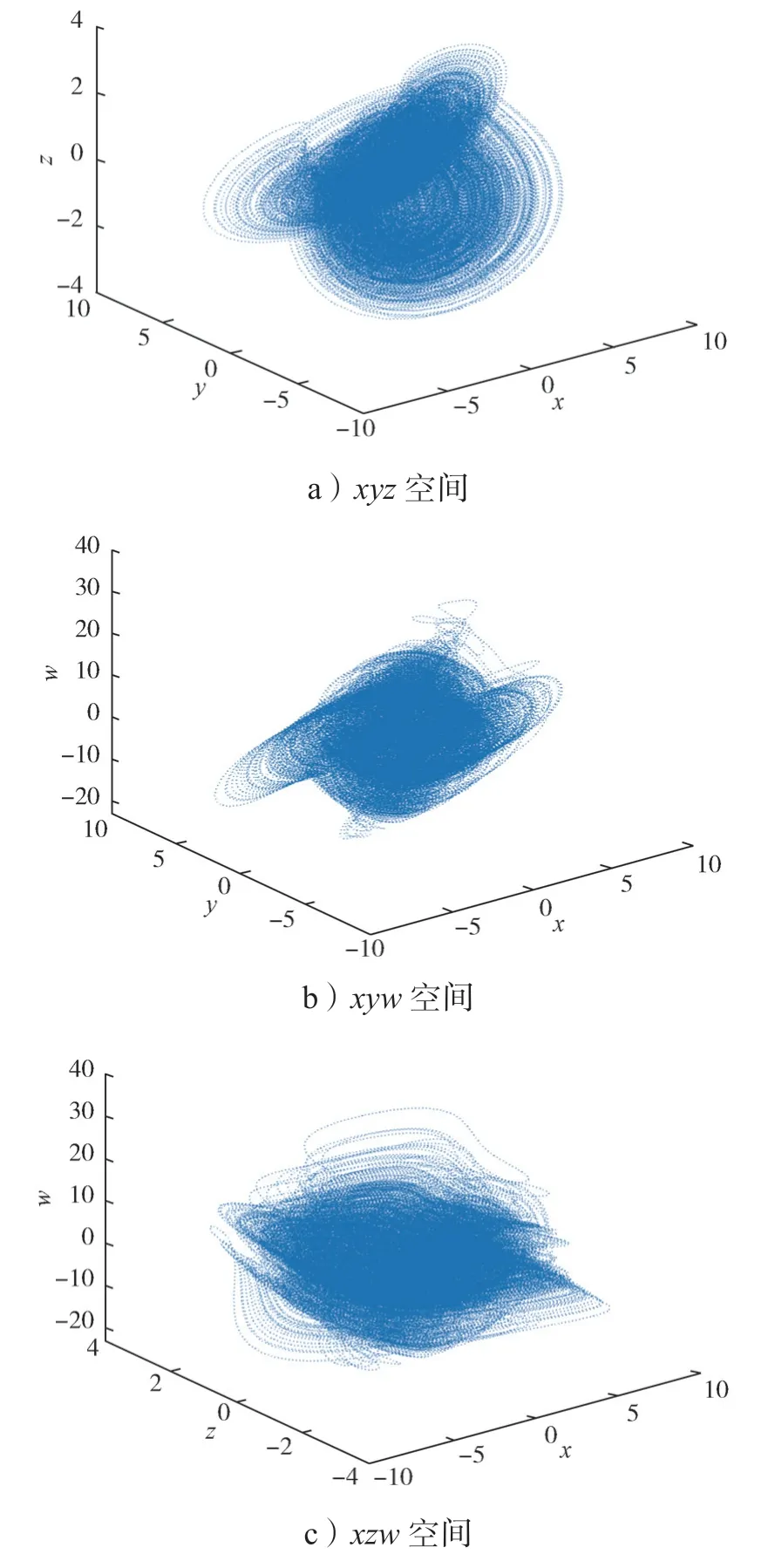
图4 e=10 时系统在三维空间中的相图Fig.4 Phase diagram of the system in three-dimensional space with e=10
此时系统(2)的庞加莱截面图如图5所示。
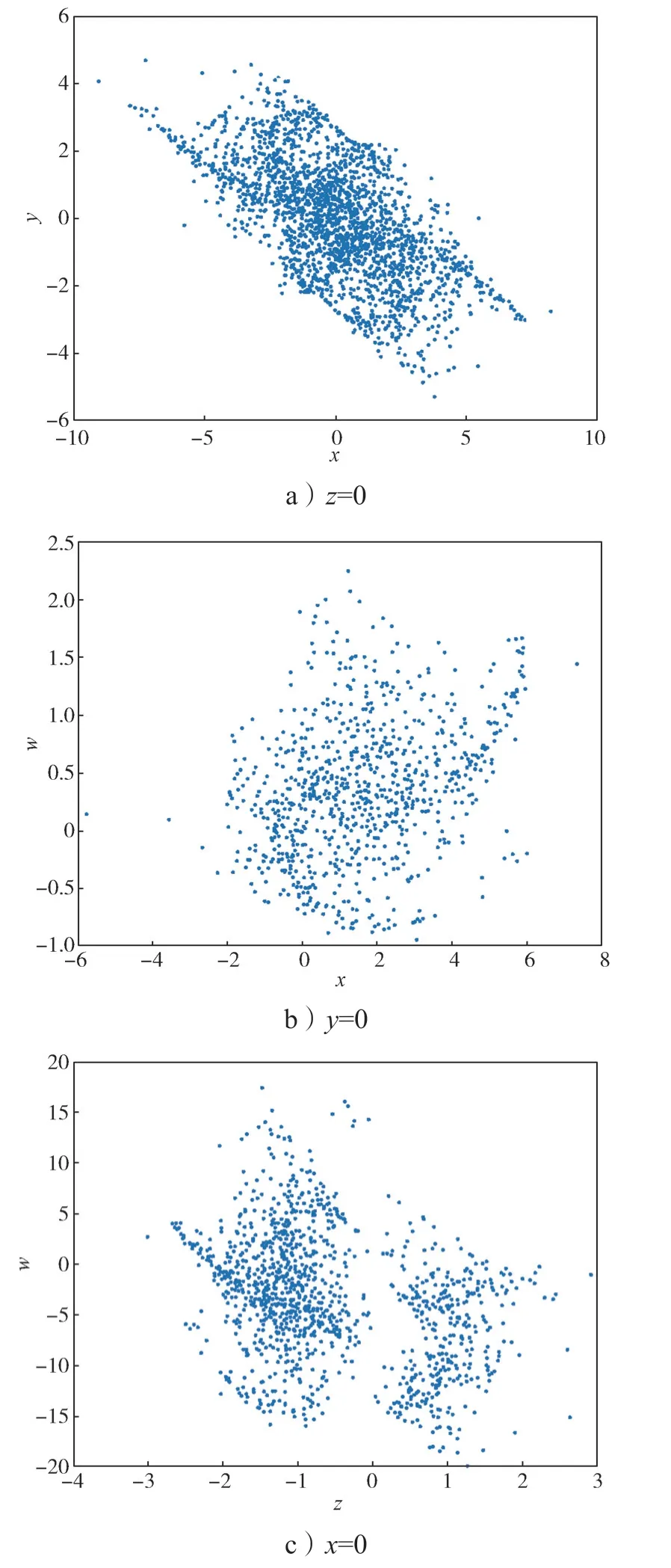
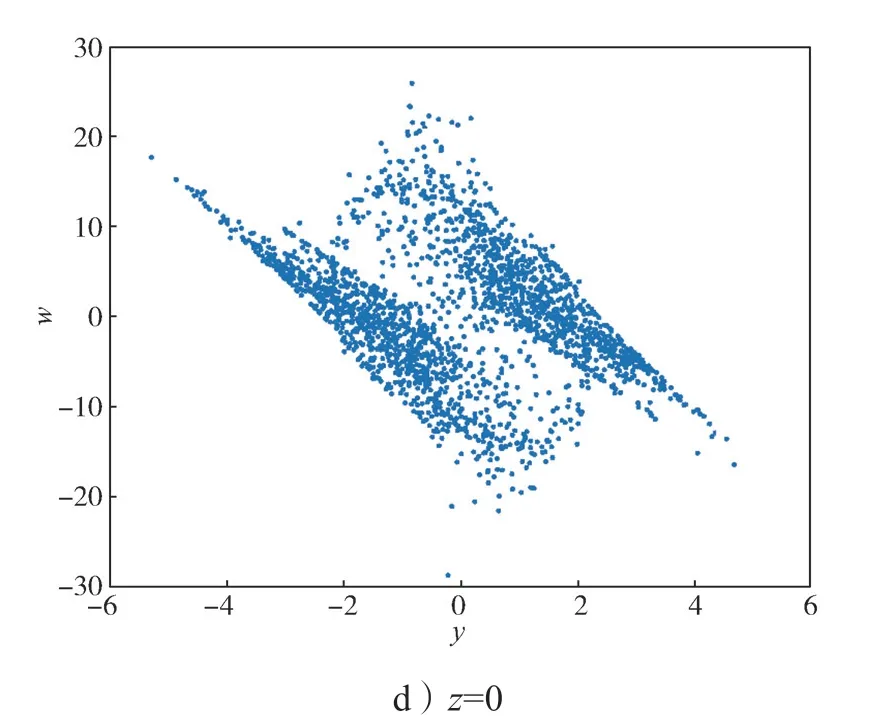
图5 e=10 时系统的庞加莱截面图Fig.5 Cross-section of the system Poincaré with e=10
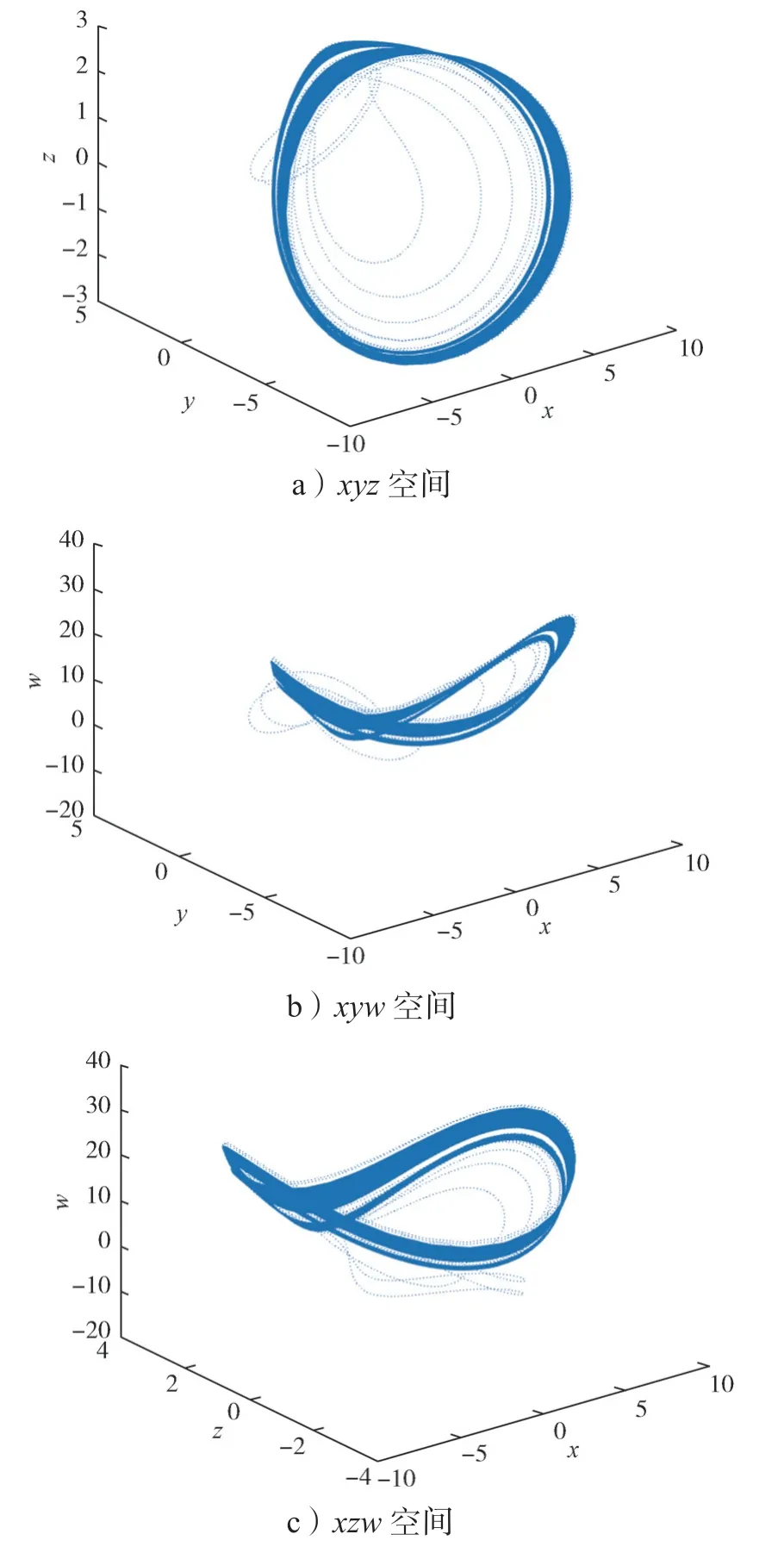
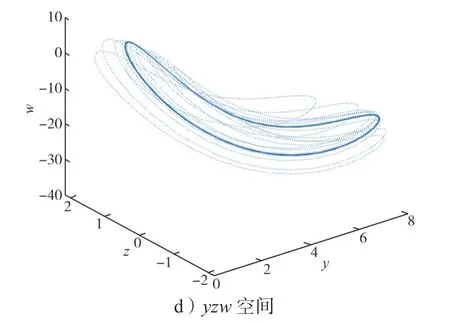
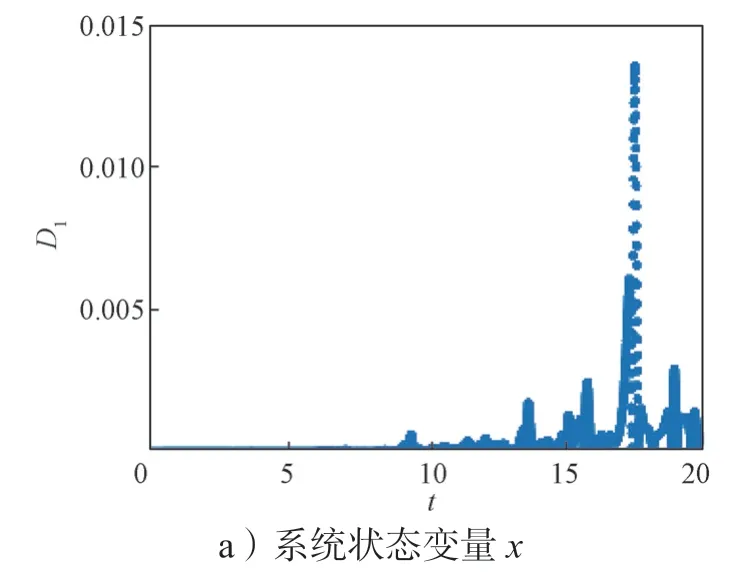
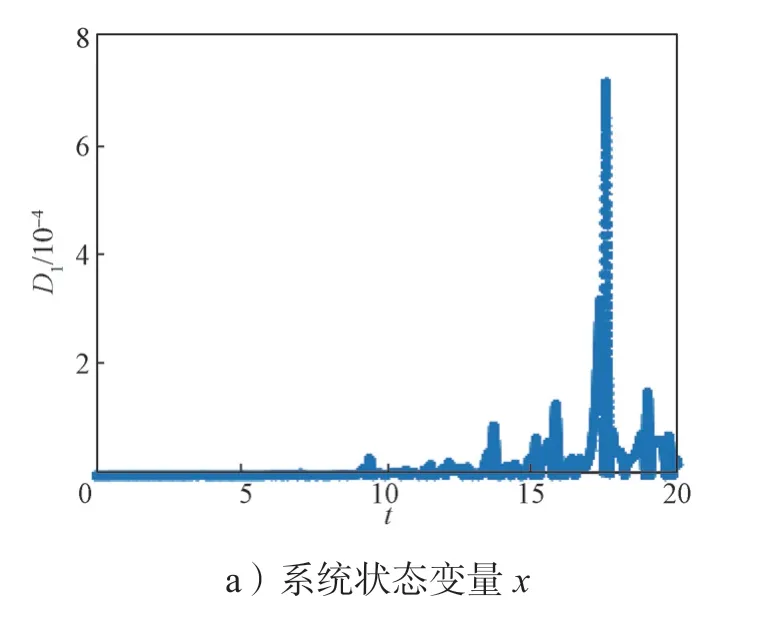
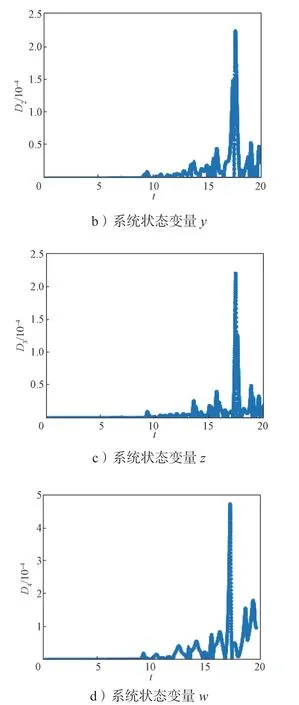
3) 当17.9 图6 e=19.5 时系统在三维空间中的相图Fig.6 Phase diagram of the system in three-dimensional space with e=19.5 此时系统(2)的庞加莱截面图如图7所示。 图7 e=19.5 时系统的庞加莱截面图Fig.7 Cross-section of the system Poincaré with e=19.5 4) 当20.1 图8 e=20.8 时系统在三维空间中的相图Fig.8 Phase diagram of the system in three-dimensional space with e=20.8 此时系统(2)的庞加莱截面图如图9所示。 图9 e=20.8 时系统的庞加莱截面图Fig.9 Cross-section of the system Poincaré with e=20.8 5)当20.9 图10 e=23 时系统在三维空间中的相图Fig.10 Phase diagram of the system in three-dimensional space with e=23 图11 e=35 时系统在三维空间中的相图Fig.11 Phase diagram of the system in three-dimensional space with e=35 由图2~11 可以看出,随着参数e取值的变化,系统分别呈现出超混沌状态、混沌状态、周期状态,混沌状态、周期状态,最后由双周期状态逐渐演变为单周期状态,系统相图、庞加莱截面图和图1 中系统的分岔图相对应,随着参数e取值的进一步增大,系统将稳定在单周期状态。参数e对系统(2)运动状态的影响具体表现如表1所示。 其中,当20.9 针对新系统(2),选定步长后,分别用有4 阶精度的二次有限元方法和4 阶经典Runge-Kutta 方法求得该系统的数值解;将步长缩减为原来的一半后,再分别用有限元方法和Runge-Kutta 方法求得该系统的数值解,最后分别将两种方法在相同节点处数值解的差值进行对比,其结果如图12~13所示。 图12 Runge-Kutta 方法所求得各状态变量在相同时间节点处数值解差值变化图Fig.12 Variationchart of numerical solutions for each state variable obtained by the Runge Kutta method at the same time node 图13 二次有限元方法求得各状态变量在相同时间节点处数值解差值变化图Fig.13 Variation chart of numerical solutions for each state variable obtained by the quadratic finite element method at the same time node 通过图12 和图13 可看出,Runge-Kutta 方法所求得的数值解,误差基本维持在10-3,而由二次有限元方法所求得的数值解,误差达到10-4,可见二次元所求的数值解更为稳定和精确。 另从图12 和图13 可以看出,各个状态变量数值解差值图随着时间的推移,相同时间节点处的数值解差值,局部会突然增大,这是由于系统(2)此时处于超混沌状态,与经过很短的时间系统的数值解曲线就会有明显变化的混沌运动特征相吻合。 根据文献[23]提出的,基于无量纲状态方程的模块化设计方法进行混沌电路设计,采用不同阻值的线性电阻、线性电容、乘法器和运算放大器实现。将系统参数代入式(2)得: 根据式(4),做模块化电路设计,如图14所示。 图14 模块化电路设计图Fig.14 Modular circuit design diagram 对应的电路状态方程为 接下来使用仿真软件进行电路模拟,设置电容C1=C2=C3=C4=0.1 μF,电阻R3=R8=R13=R18=50 kΩ,R2=R7=R12=R17=100 kΩ。因状态变量在正常变化范围内,故对变量不需进行比例压缩变换。时间尺度变换因子为100,模拟乘法器输出比例选择100 mV/V。通过式(4)和(5)的系数对比,可以得到R1=2 kΩ,R4=5 kΩ,R5=5 kΩ,R6=20 kΩ,R14=5 kΩ,R15=5 kΩ,R16=20 kΩ,并令VCC=5 V,R9=4 kΩ,得R10=20 kΩ,R11=20 kΩ。设置4 个电容的初始值均为1 V,与超混沌系统的初值[1,1,1,1]对应。供电电压选择15 V,使用Multisim 软件进行电路模拟,仿真结果与图2 一致,从而验证了该系统的可实现性。 本文在三维混沌系统的基础上,通过非线性反馈控制,构造了一个新的四维超混沌系统。分析了该系统平衡点的稳定性,并对系统的动力学行为进行了分析,发现系统随新引入的参数变化表现出非常丰富的动力学行为,随着参数取值的变化,会分别呈现出周期、混沌、超混沌状态。减半步长后,分别用二次有限元方法和4 阶Runge-Kutta 方法求得该系统的数值解,对两种方法在相同时间节点处数值解的差值进行了对比,结果表明二次有限元方法所求得的数值解精度更好。最后设计了该系统的模拟电路,验证了该系统的可实现性,为非线性系统分析提供了好的思路。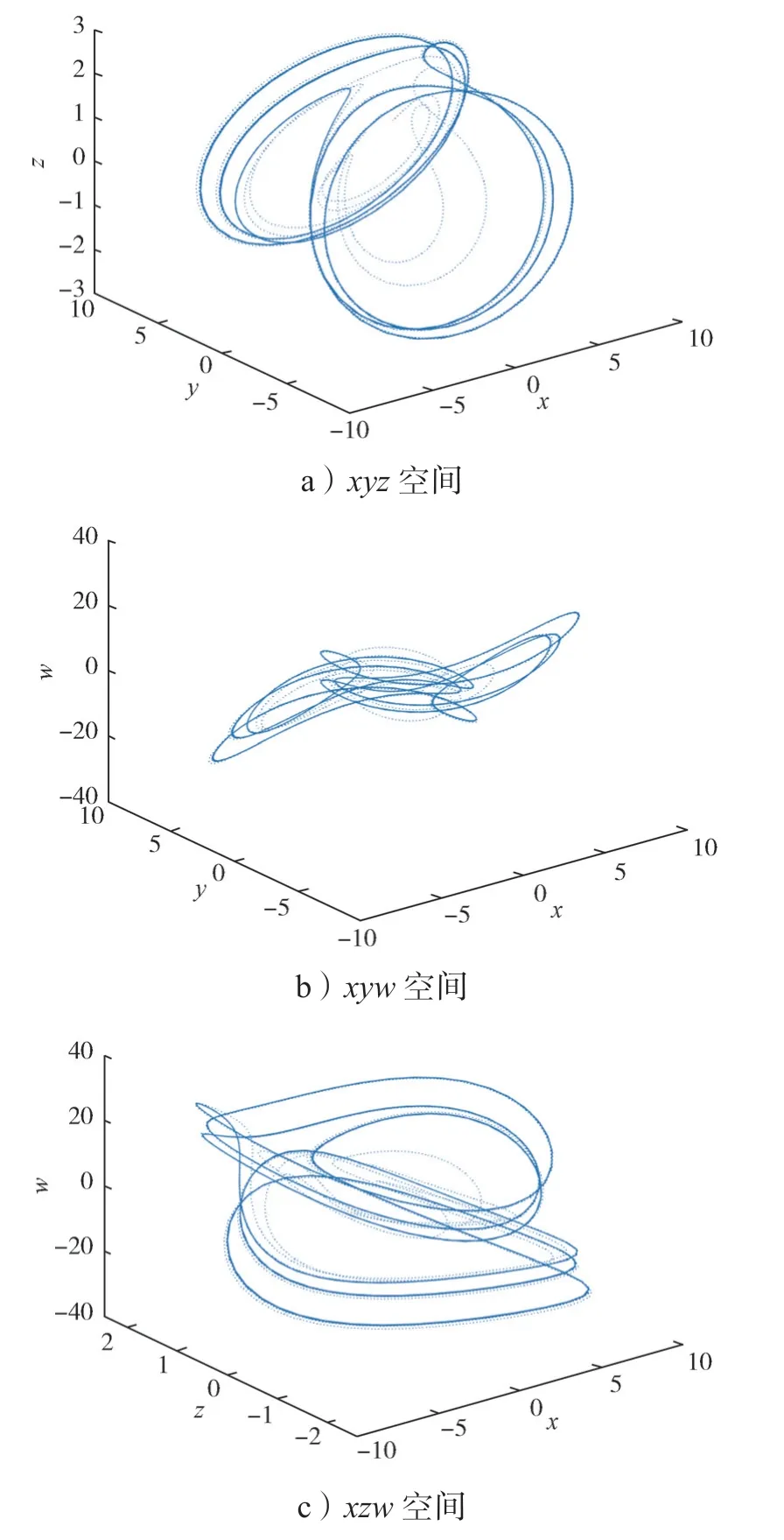
4 二次有限元方法与Runge-Kutta 方法求得的数值解对比
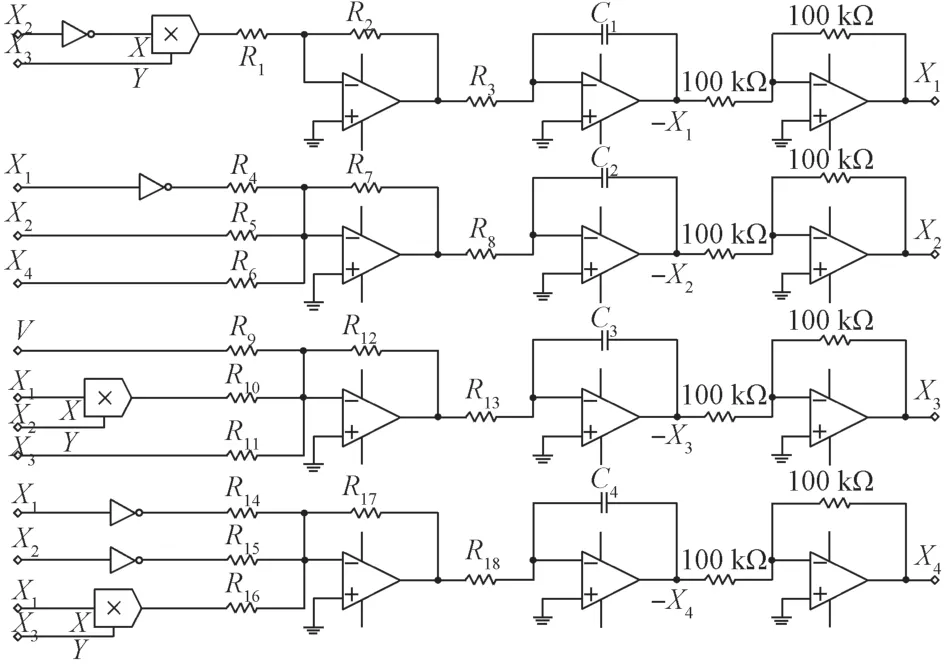
5 新系统的电路设计
6 结语
