城市固废焚烧过程烟气含氧量自适应预测控制

孙 剑 蒙 西 乔俊飞

随着人口增长、快速城市化和全球化,全球每年约产生20 亿吨城市固体废弃物(Municipal solid waste,MSW),预计到2030 年,将达到25.9 亿吨,城市固体废弃物处理问题日益突出[1].目前,对于不能直接资源回收的MSW,一般采用卫生填埋、堆肥和焚烧等方式进行处理.相比其他处理方法,城市固体废弃物焚烧 (Municipal solid waste incineration,MSWI)技术具有无害化、减容化和资源化的优点,代表了MSW 处理技术的发展趋势.截至2019 年底,中国已建有MSWI 处理厂389 座,年无害化处理固体废弃物12 174.2 万吨[2].然而,MSW成分复杂且随季节天气变化,其热值的稳定性难以保证.因此,高效、稳定的焚烧控制技术一直是MSWI 过程控制的研究重点.

烟气含氧量是焚烧炉运行过程中的重要工艺参数之一,与实际焚烧过程关系密切.若烟气含氧量不足,则说明炉内焚烧不充分,不完全焚烧热损失就会增加,飞灰含碳量也会增大;若烟气含氧量过高,则排烟损失就会增加,不仅带走大量的热量,还会增加排烟耗电量,焚烧效率也会降低.此外,烟气含氧量不足还会使炉膛中产生还原性气体,在这种气氛中,灰中熔点较高的三氧化二铁 (Fe2O3)和一氧化碳(CO)等还原性气体反应生成熔点较低的氧化铁(FeO),易造成炉膛结焦,影响生产安全[3].

在传统工业燃烧过程控制中,一般通过专家经验调节给风量和给料量,进而控制烟气含氧量.但是,由于操作员的经验、专长与水平不同,以及控制过程中经常出现的异常情况,烟气含氧量的精准控制一直是燃烧过程控制的难题之一.比例-积分-微分(Proportion-integration-differentiation,PID)控制器因具有操作简单、运行可靠和调节方便等优点,已在工业过程控制中得到广泛应用[4-6].虽然PID 控制方法原理简单,工程实现容易,但很容易产生超调或振荡,且难以胜任多输入/多输出(Multi-input and multi-output,MIMO)复杂系统的优化控制任务.随着智能控制技术的发展应用[7-9],自抗扰控制[10]、线性二次调节控制[11]、神经网络控制[12]等方法也已成功应用于各种燃烧过程的烟气含氧量控制.其中,模型预测控制(Model predictive control,MPC)是一种基于特定范围内目标函数优化的先进控制策略[13-15],能够处理有约束、多变量、多目标的控制问题,在普通燃煤锅炉、焦炭炉和流化床等燃烧过程烟气含氧量控制中已获得一些应用.例如,文献[3]建立基于最小二乘支持向量机的锅炉烟气含氧量预测模型,并在此基础上结合粒子群算法求解预测控制中的非线性优化问题,实现锅炉烟气含氧量控制.文献[16]提出一种基于混合数据驱动建模和预测函数控制策略的工业焦炉氧量调节方法.文献[17]采用数据驱动的模糊C 均值(Fuzzy C-means,FCM)聚类和子空间辨识方法对模型参数进行识别,将模型预测控制与模糊多模型相结合以控制烟气含氧量.

上述研究方法主要集中于解决MPC 应用中存在的两个关键问题,即非线性系统的预测模型建模和MPC 的非线性优化问题求解.然而,在实际工业过程中,由于设备老化、结焦污垢和外部干扰等变化,过程模型往往也会随时间发生变化,使用离线训练的机器学习模型在干扰出现后可能无法正确预测系统未来动态,最终影响模型预测控制性能[18-19].近年来,使用过程数据在线更新预测模型是处理MPC 模型失配的一种可行方案.文献[20]提出一种基于在线支持向量回归的非线性模型预测控制方法,利用在线支持向量回归的在线学习能力,实现模型在线自校正.文献[21]针对具有外部扰动和参数不确定性的非线性系统,通过多层感知机的在线训练,提出一种基于多层感知机的非线性自适应模型预测控制方法.文献[22]利用在线更新递归神经网络模型的方法,捕获过程模型存在的不确定性,并建立基于递归神经网络的预测控制方案.

针对MSWI 过程烟气含氧量难以有效控制的问题,本文提出一种数据驱动的烟气含氧量自适应预测控制方法.该方法采用自适应FCM 算法确定径向基函数(Radial basis function,RBF)神经网络隐含层神经元个数及初始中心,辅助建立准确的RBF 神经网络预测模型,并且在实时控制过程中,根据预测误差自适应调节模型参数.另外,借助梯度下降算法在滚动优化周期内优化控制目标函数,在线求解控制律,并基于李雅普诺夫稳定性理论分析控制系统的稳定性.最后,通过MSWI 厂实际数据,验证了本文方法在烟气含氧量预测建模和控制方面的可行性.

1 MSWI 过程概述及烟气含氧量自适应预测控制策略

1.1 MSWI 过程概述

MSWI 过程是通过热分解、燃烧、熔融等过程,使MSW 中的碳、氢、硫等元素与氧发生化学反应,达到无害化处理、资源化利用和快速缩减体积的目的.早期的固体废弃物焚烧炉设计和运行主要借鉴了比较成熟的燃煤技术.目前,机械炉排焚烧炉技术在中国新建的MSWI 厂中占据主流,大多数焚烧处理厂使用的机械炉排技术主要从德国、丹麦、瑞士和比利时等发达国家引进[23].本文以北京某MSWI厂使用的日本田熊公司生产的SN 型阶梯式(倾斜+水平)顺推炉排焚烧炉为例,介绍MSWI 过程,具体工艺流程如图1 所示.

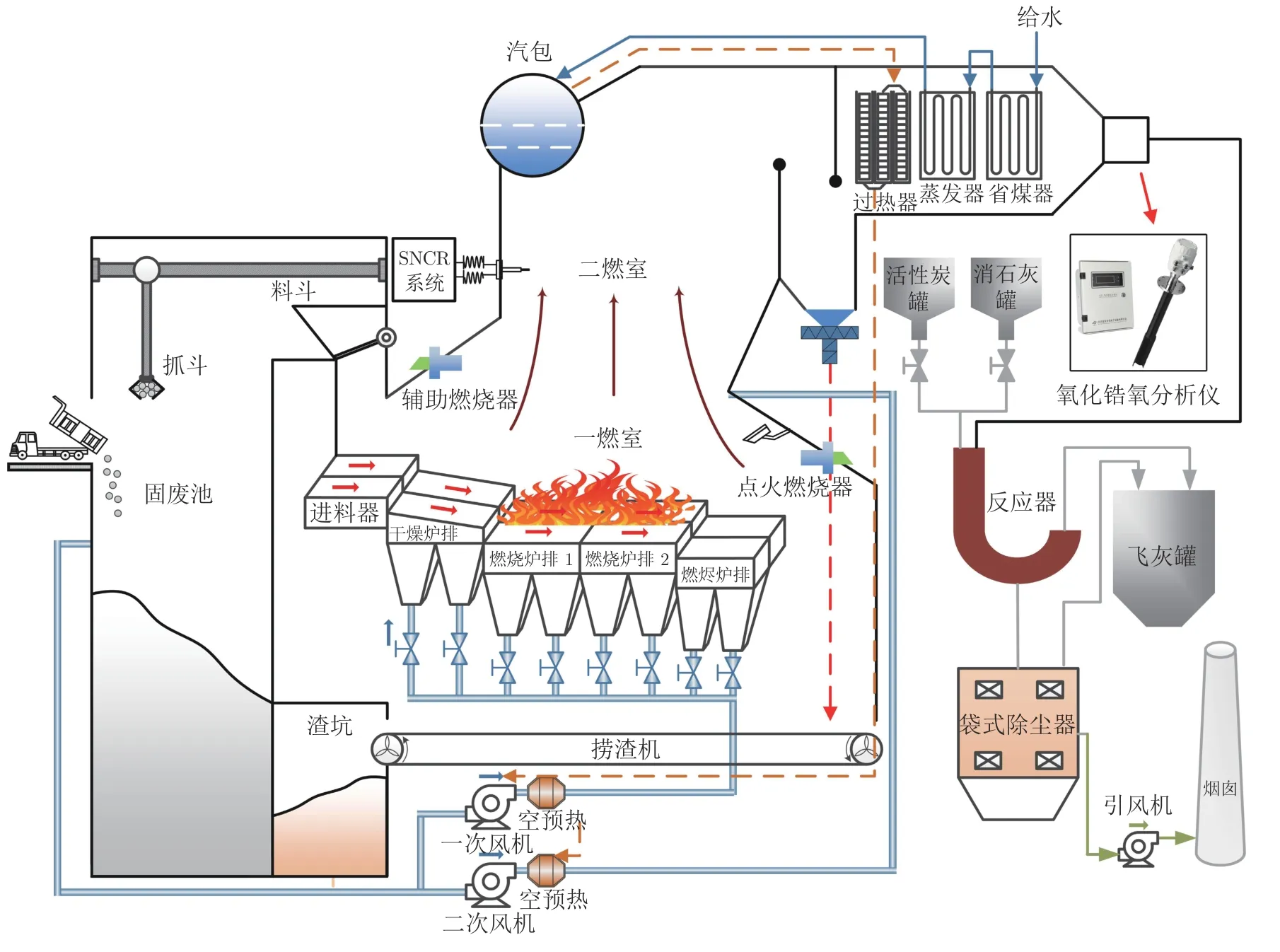
图1 MSWI 炉排炉工艺流程Fig.1 MSWI process with grate furnace

MSW 由收集车从收集点或转运站装车后被运送至固废焚烧厂,并被倾倒在一个大型的固废池中.经过5 至7 天的充分发酵,渗滤液慢慢流入渗滤液储存池.通过自然压缩、发酵作用和混合操作,可以降低MSW 含水量,提高入炉MSW 热值,获得较为均质的燃烧物,从而改善固废焚烧效果.固废池上方的抓斗混合MSW 后投入料斗.在进料器溜槽的底部,MSW 被推送至液压驱动炉排,依次通过炉排的干燥炉排、燃烧炉排1、燃烧炉排2 和燃烬炉排进行焚烧.焚烧阶段的助燃空气取自固废池,在满足MSWI 所需空气的同时,也有效防止了臭气外溢.助燃空气主要分为一次风(从炉排下方送入)和二次风(从炉排上方送入).一次风透过炉排上的气孔吹送燃烧所需的大部分氧气,二次风通过炉排上方壁的气孔加入到燃烧过程中,其主要作用是辅助炉排上方的高温烟气进行二次燃烧.当焚烧温度达到850 ℃～950 ℃时,有毒有害物质将得到充分分解.同时,为达到脱除氮氧化物的目的,采用选择性非催化还原(Selective non-catalytic reduction,SNCR)工艺,向焚烧炉内喷入尿素溶液.然后,在余热锅炉中对高温气体进行热利用,水被加热成蒸汽用于驱动汽轮发电机产生电力.烟气产物主要由氮氧化物、二噁英、碳氧化物、水、氧气、非焚烧残留物和其他酸性气体(如二氧化硫(SO2)、氯化氢(HCL))组成[24].为防止二次污染,需要采用消石灰脱酸、活性炭吸附重金属和有毒有害气体,再经过烟气净化系统的除尘操作后,净化后的烟气在引风机的作用下,经烟囱排出[25].

由上述焚烧过程分析可知,MSWI 过程是非线性且时变的复杂动态过程,内部发生着多种物理和化学反应,传热传质和多相流体流动,同时伴有高温、高压、多相耦合和多物理场共存相互作用,传统的机理建模方法很难建立准确的数学模型.而且,机理模型通常要求具有足够多能够反映工况变化的过程参数,这在很大程度上依赖于科研和工程开发人员对实际工业过程物理和化学反应过程的认识,并需要在苛刻的假设条件下才能成立,例如假定模型是一维模型、助燃剂是空气且由氧气和氮气组成、忽略挥发分析出时引起的热量变化等.因此,机理模型的精度难以得到保证,也无法满足MSWI 过程烟气含氧量控制的实际需求.针对MSWI 过程烟气含氧量控制问题,可以采用数据驱动方式建立MSWI 过程非线性系统模型,并在此基础上验证本文提出的自适应预测控制方法的有效性.

1.2 烟气含氧量自适应预测控制策略

烟气含氧量控制是MSWI 过程控制的重要一环,其稳定控制与否直接影响焚烧效率、处理成本和有毒有害污染物排放等方面.根据MSWI 过程现场控制经验,烟气含氧量一般应控制在4%～8%较为理想.目前,在中国MSWI 实际过程中,普遍采用的是人工控制和PID 控制.然而,MSWI 过程非线性和时变性的特点使得传统的控制方法难以实现精准的跟踪控制.因此,为了提高烟气含氧量的控制性能,需要研究以预测控制为代表的先进控制技术.

MPC 的控制性能很大程度上依赖于预测模型的精度,当实际系统参数发生变化时,会存在标称模型与实际系统失配的问题,此时如果仍采用标称模型的预测控制器,会导致系统控制性能变差甚至不稳定[26].为解决这个问题,本文提出基于数据驱动的自适应MPC 方法,通过实际预测误差实时在线调整预测模型的参数,使其与被控对象的动态变化保持一致.基于FCM-RBF 模型的烟气含氧量自适应预测控制(FCM-RBF neural network based MPC,FCM-RBF-MPC)策略如图2 所示,主要包括参考轨迹、基于梯度下降方法的滚动优化、基于FCM-RBF 网络的烟气含氧量预测模型和反馈校正等部分.

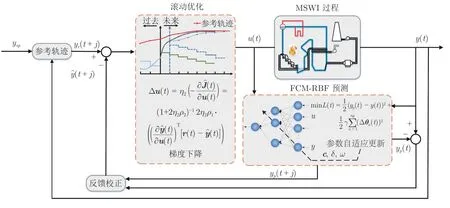
图2 烟气含氧量自适应FCM-RBF-MPC 策略Fig.2 Adaptive FCM-RBF-MPC strategy of oxygen content in flue gas

假设现在和未来控制时域内的控制动作集合为Δu(t),Δu(t+1),···,Δu(t+Hu),则通过预测模型可以预测未来时域Hp内的系统输出一般要求控制时域Hu小于预测时域Hp.通过设计模型预测控制器,将烟气含氧量的参考值跟踪问题转化为最小化目标函数式(1)的优化问题.本文采用在线梯度下降方法求解该优化问题:

1)参考轨迹.为了把当前输出y(t)平滑地引导到设定值ysp(t),采用一阶平滑滤波形式将参考轨迹设置如下:

式中,ar是调整因子,0＜ar＜1.

2)反馈校正.由于容易受到系统干扰或模型失配等因素影响,预测模型输出yp(t)与实际输出y(t)之间会存在偏差.为了缩小这种偏差,一般利用被控对象实际输出与预测模型输出的偏差进行反馈补偿[27].MPC 通过滚动优化目标函数的方式确定一系列未来的控制动作后,它们并不会都逐一实施,而只执行当前控制输入.此外,通过比较当前时刻的实际输出与预测模型输出,得到两者的偏差,并用于校正模型下一时刻的预测值,从而使得预测结果更为准确.具体校正公式如下:

2 数据驱动FCM-RBF 烟气含氧量预测建模

预测模型是模型预测控制算法的基础,因此需要首先建立烟气含氧量的预测模型.预测模型的作用是根据设定的输入以及历史信息来预测被控对象未来的输出.在建立非线性动态预测模型时,系统可以表示为以下形式的非线性自回归外生模型:

式中,u(t)和y(t)表示过程的输入和输出,f[·] 是MSWI 过程烟气含氧量的预测模型,ny和nu是输出和输入的最大滞后.在忽略噪声作用情况下,对于式(5)所表示的系统,当获得过去的输入/输出信息后,系统的输出估计yp(t)可以借助已建立的神经网络预测模型得到.因此,为得到准确的输出估计,需要建立能够反映系统动态的预测模型.

2.1 RBF 网络结构

RBF 网络是由输入层、隐含层和输出层构成的前向网络,因其简单直观的结构和优良的逼近能力,RBF 网络一直是神经网络领域研究的热点[28].输入层节点个数等于输入向量的维数,输出层节点个数等于输出向量的维数,隐含层神经元个数根据需要确定.单输出结构的RBF 网络如图3 所示.隐含层节点的激活函数采用较为常见的高斯函数:

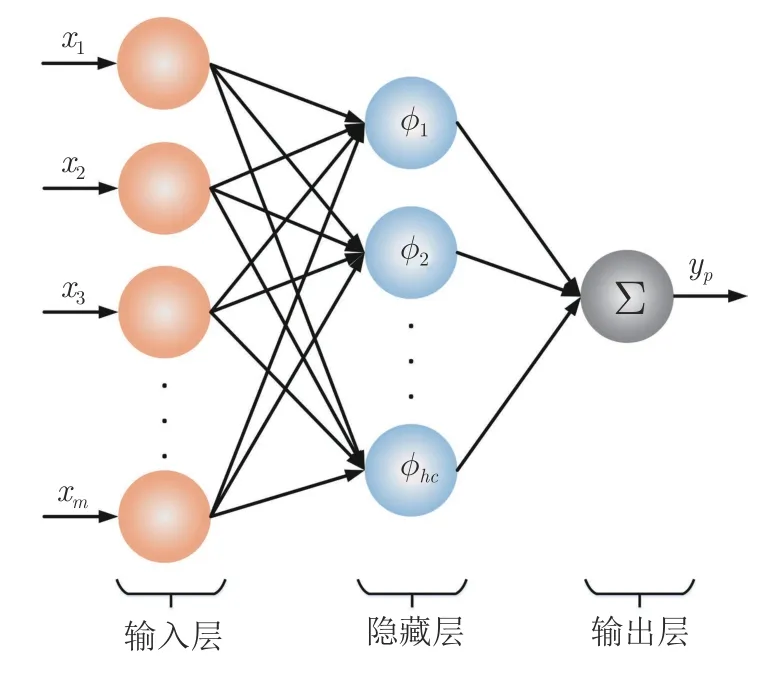
图3 RBF 神经网络结构图Fig.3 RBF neural network framework

网络输出为:

式中,x=(x1,x2,···,xm)T为l维输入变量,hc代表隐含层神经元个数,yp表示输入为x时网络的输出,ωj为隐含层第j个神经元到输出层的权值,cj和δj分别是第j个神经元的中心向量和宽度.采用梯度下降法对网络参数进行调整.

对于第t个样本,网络实际输出和期望输出之间的误差e(t)定义为:

式中,y为实际值,N为样本个数.隐含层第j个神经元的中心cj、宽度δj和输出权值ωj更新公式如下:

式中,η1为学习率,具体梯度公式如下:

2.2 FCM-RBF 网络

在RBF 神经网络建模过程中,隐含层神经元个数、中心、宽度和网络权值等参数初始值通常使用人工试错验证的方法来确定,所选参数初始值直接影响RBF 神经网络建模效果,其中RBF 隐含层神经元个数和初始中心对建模效果影响较大.FCM算法是一种基于划分的聚类算法,基本思想是使被划分到同一类的对象之间的相似度最大,而不同类之间的相似度最小[29],但是需要人为给定初始聚类数目.因此,利用自适应FCM 聚类算法迭代计算出训练样本的聚类数目和聚类中心,作为RBF 神经网络的隐含层神经元个数和初始中心.

假设P={p1,p2,···,pn}是一个有限数据集,其中,pg=(pg1,pg2,···,pgl)是第g个一维对象,B={b1,b2,···,bb}表示b个聚类,V={v1,v2,···,vb}表示b个l维聚类质心,U=(uig)(b×n)是模糊划分矩阵,uig是第g个对象在第i个聚类中的隶属度,其中:

目标函数是每个聚类中样本到聚类质心的加权距离平方和,即:

式中,dig=‖pg-vi‖表示第g个对象和第i个聚类质心之间的欧氏距离.m(m＞1)是模糊指数,控制着类群之间模糊重叠的数量,值越大,表示重叠的程度越大.

根据聚类准则,适当地模糊划分矩阵U和聚类质心V,可以通过最小化目标函数JFCM获得,基于拉格朗日乘子方法,U和V分别由下式计算:

为了使类间距离应尽可能大,类内距离应尽可能小,采用如下有效性函数衡量聚类效果,自适应确定模糊聚类数目[30]:

上述有效性函数LFCM(b)表示类间距离之和与类内距离之和的比值,所以,LFCM(b)越大,表示聚类结果越可靠.当LFCM(b)达到最大值时,聚类数目b为最佳聚类数目.其中,表示整体数据的中心向量:

自适应FCM 算法通过最小化目标函数JFCM的迭代过程来实现更新U和V,具体步骤如下:

1)分配初始值的聚类数目b=2、LFCM(1)=0、模糊指数m、最大迭代次数Imax和阈值ξ;

2)根据隶属度的约束,随机初始化模糊划分矩阵U(0);

3)根据式(18)计算b类聚类质心V(s);

5)根据式(17)计算U(s+1),返回步骤3);

6)计算LFCM(b).如果LFCM(b-1)＞LFCM(b-2)且LFCM(b-1)＞LFCM(b),则停止迭代;否则,执行b=b+1 并转至步骤3).

2.3 模型参数自适应更新

由于城市固体废弃物成分的不确定性、操作员操作水平的差异性以及外部干扰的随机性影响,难以用离线的非线性预测模型准确刻画时变的MSWI 动态过程.此外,当实际过程的结构参数发生变化时,容易造成模型失配,会导致预测模型输出和实际系统输出之间的误差增大,进而影响预测控制效果.为此,在控制过程引入模型参数自适应更新策略[31],在保证实际系统输出与预测模型输出间误差最小的同时,让每一时刻预测模型参数的变化也尽可能小,在线调节预测模型参数.模型参数自适应更新的目标函数定义如下:

式中,γ＞0 为权系数,用以控制参数的变化速度,θ为FCM-RBF 预测模型中的参数{c,ω,δ},nθ为模型参数的个数.

对式(21)可以采用如下梯度下降公式更新参数向量:

当满足设定精度要求或最大迭代次数的更新终止条件后,即可求得t时刻自适应调整后的预测模型参数.

3 烟气含氧量自适应预测控制过程

3.1 在线梯度优化控制

在线优化控制的基本思想是在MPC 未来的控制序列中,选择当前的控制输入来最小化目标函数[32].目标函数由以下向量重新定义:

式中,η2＞0 是梯度下降的学习率.由式(27)易知:

将式(29)代入式(28),则:

式中,n=1,2,···,Hp,m=1,2,···,Hu.由文献[33]可知,式(34)可简化为:

对于RBF 网络:

其中

当控制时域Hu为1 时,预测控制器的计算量较少,可以克服该控制方法在求解优化问题时需要进行较大的矩阵运算问题,并取得令人满意的控制效果[34].因此,本文设置Hu=1,则式(31)可表示为:

3.2 稳定性分析

需要指出的是,用式(31)计算的最优控制输入序列必须满足稳定的MPC 迭代过程.控制权重参数ρ1和ρ2一般取正数,控制律序列的学习率η2只影响优化速度,而且η2的波动与控制稳定性无关.

定理1.将µ定义为FCM-RBF-MPC 优化过程的参数,如式(39)所示,如果其满足下式条件,则该过程就是稳定的:

式中,λmax是g(t)gT(t)的最大特征值.

证明.为了分析稳定性,定义如下的李雅普诺夫函数:

则李雅普诺夫函数VC的差分形式为:

易知,E(t)的时间导数为:

式中,I是一个Hp阶的单位矩阵.

引理1.定义矩阵函数 (kI-A)X=0,其中A是Hp×Hp阶的对称矩阵,X是Hp×1 阶的向量.则A的特征值可以表示为k(a)=其中

利用式(45)和引理1,根据式(41)设置最优参数µ,可得 ΔVC(t)＜0.根据李雅普诺夫稳定性理论,采用一阶梯度优化方法的FCM-RBF-MPC 过程是稳定的.

3.3 实现步骤

本文以特定工况下的MSWI 数据驱动过程模型为研究对象,借助现场运行数据,首先,建立基于FCM-RBF 网络的烟气含氧量预测模型,使用自适应FCM 算法,确定RBF 网络隐含层神经元个数及初始中心;其次,通过反馈校正环节对预测模型结果进行修正,并采用模型参数自适应更新策略在线更新预测模型参数;最后,采用梯度下降方法,在线求解每一时刻的最优控制量.烟气含氧量自适应预测控制算法的实现步骤如下:

1)选择合适的参数.包括RBF 神经网络参数如学习率η1、网络权值等;控制参数如预测时域Hp,控制时域Hu,参考值调整因子ar,控制权重因子ρ1、ρ2,控制输入的学习率η2和模型参数自适应更新学习率λ.

2)选择特定工况下分散控制系统采集的输入/输出数据构成样本集,划分为训练集和测试集,并进行数据归一化处理.使用自适应FCM 算法确定RBF 神经网络隐含层神经元个数及初始中心,离线训练FCM-RBF 神经网络预测模型.

3)给定烟气含氧量的设定值,并通过式(2)计算参考估计yr(t+i),i=1,2,···,Hp.根据已知的系统控制量u(t),系统实际输出y(t),计算实际输出与预测输出之间的偏差err(t).

4)在第t+1 时刻,基于历史输入/输出数据,通过FCM-RBF 网络预测模型,可迭代求得预测输出yp(t+i),然后通过偏差err(t)修正该预测输出.

5)在预测时域Hp内,使用梯度下降方法得到雅可比矩阵依据式(31)计算控制时域Hu内的控制增量序列 Δu,并代入被控对象的数据驱动模型,得到系统实际输出.

6)利用梯度下降法求解式(21)预测模型参数自适应优化问题,更新FCM-RBF 预测模型参数.

7)返回步骤3),重复整个过程.

4 仿真实验与分析

本文使用的数据来自于现场分散控制系统采集的3 800 组实测数据,采样间隔时间为1 s.选取2 660组数据(占70%)作为训练样本,1 140 组数据(占30%)作为测试样本,建立基于自适应FCM-RBF网络的离线预测模型,并在控制过程中采用模型参数自适应更新策略在线更新模型.为评估本文控制方法的有效性,利用带有外部干扰的城市固废焚烧过程烟气含氧量控制实验进行实验验证.

4.1 自适应FCM-RBF 网络的烟气含氧量预测性能

由于MSW 成分繁杂和焚烧过程的不确定性,实际MSWI 过程的运行情况复杂多变.MSW 质量流量和负荷波动是工况变化的重要表现,但是现场很难直接获得具体数值.而给料速度调节量和炉排速度调节量能够间接表征MSW 质量流量和负荷变化,从而识别不同工况.其中,炉排速度调节量又分为干燥炉排、燃烧炉排1、燃烧炉排2 和燃烬炉排共4 个区间,每段炉排下方分别对应有一次风流量分量.为设计和说明方便,本文仅对给料速度和各阶段炉排速度调节量稳定时的一种典型工况进行建模研究.在该种工况下,烟气含氧量(yo)被限定为主要与风量,即干燥炉排一次风流量xp1、燃烧炉排1 一次风流量xp2、燃烧炉排2 一次风流量xp3、燃烬炉排一次风流量xp4和二次风流量xs有关.所选输入/输出变量数据变化范围见表1.

表1 输入/输出变量变化范围Table 1 Range of input and output variables

为避免输入变量物理意义和单位不同对结果的影响,需要首先进行数据归一化预处理.此外,选取合适且精简的特征变量是模型准确构建的前提,操作变量与烟气含氧量的皮尔森相关系数γ如表2 所示,需要剔除[-0.11,0.11]范围内相关性弱的变量,即最终选择干燥炉排一次风流量xp1、燃烧炉排1一次风流量xp2和二次风流量xs作为特定工况下的操作变量,烟气含氧量yo作为被控变量.

表2 操作变量与烟气含氧量的皮尔森相关系数Table 2 Pearson correlation coefficient between manipulated variables and oxygen content in flue gas

在建立烟气含氧量预测模型时,选取模型输入/输出阶数ny=nu=2,则预测模型的输入变量可写为如下形式:

通过试凑法确定,设置自适应FCM 算法模糊指数m为5,最大迭代次数Imax为100,阈值ξ为0.00001,最终得到最优聚类数目b为26.将该最优聚类数目作为RBF 网络隐含层神经元个数,聚类中心作为神经元的初始中心.初始权值、宽度随机设置,学习率η1=0.05,训练的期望均方误差(Mean square error,MSE)设为0.01,最大训练步数为200 步,采用梯度下降法对该网络进行训练.本文FCM-RBF 神经网络与多层感知机(Multi-layered perceptron,MLP)神经网络、RBF 神经网络的烟气含氧量预测效果如图4 所示.

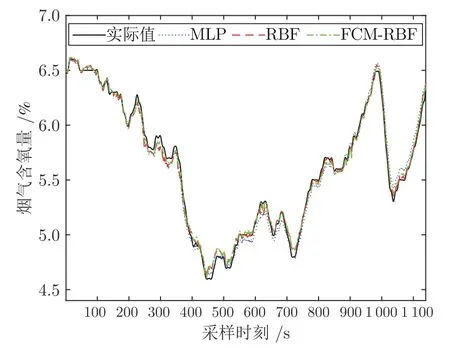
图4 不同建模方法的烟气含氧量预测效果Fig.4 Prediction effect of oxygen content in flue gas with different modeling methods

由图4 可以看出,RBF 神经网络和FCM-RBF神经网络的烟气含氧量预测准确性均优于MLP 神经网络,但在波峰和波谷位置,两种网络仍有较明显的预测偏差.为了进一步验证FCM-RBF 神经网络预测烟气含氧量的有效性,采用均方根误差(Root mean square error,RMSE)、平均绝对百分比误差(Mean absolute percentage error,MAPE)和平均绝对误差(Mean absolute error,MAE)评估预测性能.表3 列出了不同模型独立运行30 次的预测性能指标平均值.

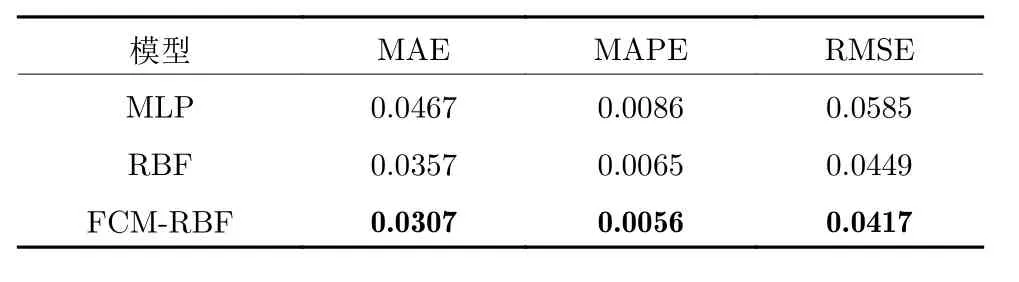
表3 不同建模方法的烟气含氧量预测评价指标对比Table 3 Comparison of prediction evaluation indexes of oxygen content in flue gas with different modeling methods

式中,yd(t)、yp(t)和Q分别为观测值、预测值和样本数.

在表3 中,FCM-RBF 神经网络预测烟气含氧量的MAE、MAPE 和RMSE 分别为0.0307、0.0056和0.0417,与MLP 神经网络和RBF 神经网络相比,FCM-RBF 神经网络的预测性能指标有明显提升.这是因为自适应FCM 算法能够帮助确定较优的RBF 神经网络隐含层神经元个数及初始中心,降低随机初始中心带来的不确定性,提高RBF 神经网络的预测精度.该模型能够为模型预测控制提供反映MSWI 过程烟气含氧量动态特性的精准预测模型.

4.2 自适应FCM-RBF-MPC 的烟气含氧量控制性能

为了验证本文的自适应FCM-RBF-MPC 方法的有效性,对比了基于不同RBF 神经网络预测模型的烟气含氧量控制效果.选取预测时域Hp为5,控制时域Hu为1,参考值调整因子ar为0.1,控制权重因子ρ1和ρ2为1 和150,控制输入的学习率η2为0.1,参数自适应更新学习率λ为0.05,最大更新步数为200 步,模型更新的期望均方误差设为0.01,控制时间间隔为1 s.由于MSWI 实际过程存在不确定性干扰,为了模拟这种情况,在100 s 和300 s处起分别施加幅值为0.2 和0.5 的干扰v(t)如下:

考虑焚烧过程动态特性的非线性和不确定性,需要跟随变化的烟气含氧量设定值,并自适应调整控制器输出.为了测试本文设计的自适应FCMRBF-MPC 控制有效性,对比实验选取了采用RBF、FCM-RBF 和自适应RBF 神经网络作为预测模型的数据驱动MPC.烟气含氧量变设定值的FCMRBF-MPC 和自适应FCM-RBF-MPC 控制器跟踪效果如图5 所示,操作变量具体变化如图6 所示,反馈校正误差补偿变化情况如图7 所示.由图5 可以看出,与FCM-RBF-MPC 方法相比,自适应FCM-RBF-MPC 方法能够更及时地给出准确的控制输出,使系统能够更快地跟踪烟气含氧量的参考轨迹.由图7 可以看出,预测误差err(t)在控制起始阶段、设定值变化阶段和干扰施加初始阶段的变化比较明显,说明这些阶段中的模型自适应更新预测结果与实际值仍存在较大偏差.当达到模型自适应更新的终止条件,而预测结果与实际值仍存在偏差时,反馈校正可以作为模型自适应更新的误差补偿来修正预测结果.

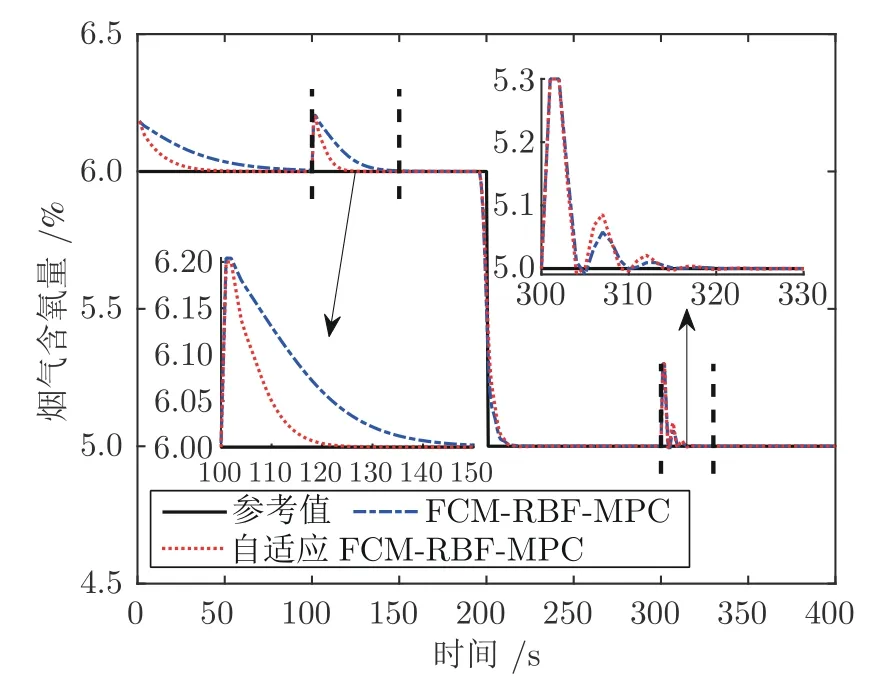
图5 FCM-RBF-MPC 和自适应FCM-RBF-MPC 控制效果Fig.5 Control results of FCM-RBF-MPC and adaptive FCM-RBF-MPC

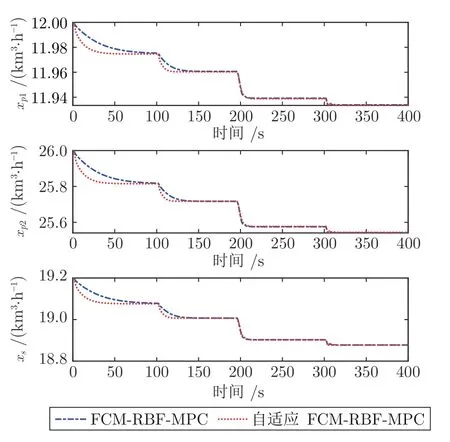
图6 FCM-RBF-MPC 和自适应FCM-RBF-MPC的操作变量变化情况Fig.6 Changes of manipulated variables of FCM-RBF-MPC and adaptive FCM-RBF-MPC

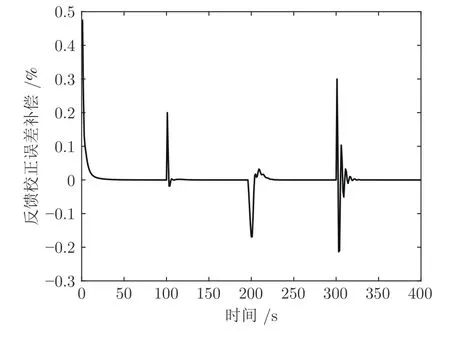
图7 反馈校正误差补偿变化情况Fig.7 Changes of feedback correction error compensation

此外,采用绝对误差积分(Integral of absolute error,IAE)[35]、绝对误差与时间乘积积分(Integral time absolute error,ITAE)[35]和最大绝对误差(Maximal deviation from set-point,Devmax)[36]评价控制效果,具体公式如下:

式中,K是样本总数,eOC代表烟气含氧量参考值与真实输出值之间的误差.

表4 给出了不同RBF 神经网络预测控制器用于烟气含氧量控制的评价指标对比结果.可以看出,自适应FCM-RBF-MPC 的IAE、ITAE 和Devmax分别为0.0031、2.4152 和0.4226,与FCM-RBF-MPC算法相比,分别降低了27.90%、19.50%和14.61%;与自适应RBF-MPC 算法相比,分别降低了31.11%、30.23%和2.51%.结果表明,在给定的烟气含氧量变设定值情况下,本文提出的自适应FCM-RBFMPC 方法具有更好的自适应性和抑制干扰能力,能够对烟气含氧量实现更精准的控制.

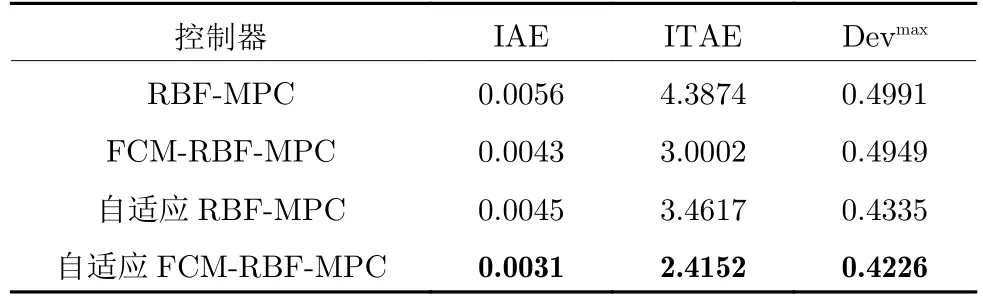
表4 不同RBF 神经网络预测控制器性能指标对比Table 4 Comparison of evaluation indexes of different RBF neural network predictive controllers

5 结束语

面向MSWI 过程烟气含氧量精准控制需求,本文提出一种自适应模型预测控制方法.首先,为降低随机初始RBF 隐含层神经元个数及初始中心带来的不确定性,建立基于数据驱动的自适应FCMRBF 神经网络烟气含氧量预测模型;其次,在控制过程中采用模型参数自适应调节策略,提高了预测模型的动态自适应性;接着,利用梯度下降方法方便快速地求解MPC 控制律,并基于李雅普诺夫稳定性理论证明了控制系统的稳定性;最后,基于MSWI厂实际数据建模和控制实验,表明本文自适应FCMRBF 网络建模方法具有较高的预测精度,本文自适应FCM-RBF-MPC 方法相对于其他RBF 神经网络预测控制器,具有更好的设定值跟踪性能,验证了该方法在干扰存在情况下,仍然具有很好的自适应控制能力.后续将进一步研究该方法的节能应用效果和预测模型结构在线自适应调整机制捕获更多未知工况.