基于时间差分误差的离线强化学习采样策略

张龙飞，，梁星星，刘世旋，程光权，黄金才

国防科技大学系统工程学院，长沙 410073

近年来，强化学习技术凭借其自主学习的优势在游戏[1]、自动驾驶[2]、核能利用[3]、算法发现[4]和兵棋推演[5]等领域取得重要进展.与传统基于搜索的决策算法不同，强化学习通过与环境交互试错，根据获取的反馈奖励学习状态-动作的价值函数，不断学习更新行动策略.这种数据驱动的学习方式决定了强化学习的策略学习依赖于大规模的学习数据，存在训练效率低、学习收敛慢、过程不稳定等问题.为此，研究者们提出离策略（Off-Policy）强化学习方法，比如异步优势演员-评论者（A3C）[6]、软性演员-评论者（SAC）[7]、双延迟深度确定性策略梯度（TD3）[8]等，基于模型的强化学习方法，比如深度规划网络（PlaNet）[9]、想象者（Dreamer）[10]、想象者-v2（Dreamer-v2）[11]等，可以有效提升样本利用率、加快学习效率.尽管这些方法在多个复杂决策和控制任务上展现出优异性能，但仍需通过与环境交互获取训练数据，属于在线强化学习方法的范畴.

与在线强化学习方法不同，批量-约束的深度Q 学习（BCQ）[12]、基于数据增强的离线强化学习方法（ORAD）[13]、基于模型的离线-在线强化学习方法（MOORE）[14]，双延迟深度确定性策略梯度-行为克隆（TD3-BC）[15]等离线强化学习方法，是指智能体无需与环境进行实时交互，而是利用预先收集的离线数据，在离线的情况下学习策略.在交互成本高、在线样本采集难的场景下，离线强化学习方法具有一定节省交互成本、降低交互风险的优势.然而，离线强化学习不与环境交互的特性，也给其训练带来了“外推误差”的问题.当离线训练的智能体在实际环境中进行交互时，会对训练时未见过的新状态、新动作出现乐观估计，导致学习的价值函数估计误差累积，从而引发性能下降.为此，大量离线强化学习方法通过在目标函数中增加惩罚项、正则项等方式，使离线学习的策略保持在预先收集的数据分布的附近，从而约束了离线学习的策略在实际环境中的过度探索.尽管这些方法在一定程度上缓解了外推误差的问题，但因引入了额外的约束项和超参数，使得训练更为复杂，限制了其在实际场景中的推广应用.

本文提出一种基于时间差分误差的采样策略，通过将优先经验回放的优先采样方法与标准经验回放的标准采样方法相结合，在不同的训练阶段采用不同的训练机制，以提升训练效率，降低样本采样率.然而，以往的研究经验表明，使用优先经验采样会因采样偏好导致出现训练偏差，为消除这种偏差，本文使用重要性采样机制.时间差分误差作为强化学习中衡量策略优劣的指标，通常被用于优先采样的优先度.本文结合离线强化学习算法—保守Q 估计离线强化学习方法[16]（Conservative Q-learning for offline reinforcement learning，CQL），基于不同的目标函数估计方法，比较了以3 种不同的时间差分误差值作为优先采样的优先度度量指标时的算法性能.经过在离线数据集—深度数据驱动强化学习数据集（Datasets for deep data-driven reinforcement learning，D4RL）上的实验可以看出，本文的方法在样本利用率、最终性能和训练稳定性上都明显优于其他同类算法[17].此外，通过消融实验也可发现，优先采样和标准采样相结合的采样方式是本文算法的关键.同时，使用最小化双Q 值目标估计的时间差分误差优先度度量所对应的算法，在多个任务上具有最优的性能.本文的方法主要贡献如下：（1）提出了一种新的包含优先采样和标准采样的离线强化学习采样策略，可有效提升样本效率；（2）比较了3 种基于时间差分误差的优先度度量指标所对应的算法的性能.本文的方法聚焦于样本采样策略，无需在算法的目标函数中额外引入偏置归纳项，避免了对原始算法的修改，易于与其他离线学习算法结合，具有较好的实用性和可扩展性.

1 强化学习中的采样方法

1.1 基于经验回访池的采样方法

强化学习需利用智能体和环境交互产生的数据不断更新策略直至收敛，这些数据往往质量不一、标签稀缺，且无法重复使用.为提升数据利用率，强化学习引入了经验回放机制，即将智能体与环境在一定时间段内交互生成的数据存储起来组成一个经验池，训练时再从经验池中采集训练样本.为保持样本的多样性，一般都使用随机采样的方法.优先经验回放（Prioritized experience replay，PER）则是考虑到数据的质量不同，部分具有更高价值的训练数据应被更多次采样，因此使用每条数据的时间差分误差值来定义优先度，每次训练时按照数据的优先度进行采样，可有效提升样本利用率[18].此外，竞争经验回放（Competitive experience replay，CER）通过使用双经验回放池，从2 个经验池中采样训练数据，鼓励2 个智能体相互竞争实现对环境的探索，引导智能体在目标导向的任务中探索出最优策略[19].Fu 等[20]在优先采样策略的基础上，定义了时间差分误差、N步奖励返回值、虚拟计数、似然估计、通用自模仿学习、虚拟计数6 种不同的优先度指标，通过大量实验表明，以上指标均可有效提升离线强化学习的采样效率.Lee 等[21]提出针对离线训练的智能体在线微调再学习时，易因数据分布偏差产生严重的自举误差的问题，使用一个平衡的经验回放机制，优先采样遇到的在线样本，同时也鼓励使用来自离线数据集的接近策略的样本，该方法主要是解决数据分布偏差问题，并未对离线数据本身进行优先度度量以提升学习效率.

1.2 时间差分误差

时间差分误差是智能体自举产生的目标值与价值网络评估值之间的差异，反映的是在当前策略和价值函数下，状态或状态-动作对的相对优劣，是对状态或状态-动作对的评估指标[22].按照时间差分中使用的自举步数，可将其分为1 步时间差分和N（N＞1）步时间差分.PER 使用1 步时间差分误差作为数据元组优先度的度量指标，并把数据存储在SumTree 结构中，每次按照优先采样方式采集出批量数据进行训练，并在每次网络更新后重新计算时间差分误差，以赋予数据元组新的优先度.PER 使得时间差分误差值大的数据获得更多采样次数，有效提升了深度Q 网络算法（Deep Q-network，DQN）的样本利用率和最终性能.Rainbow 则是采用N步返回值计算时间差分误差，通过N步返回值计算目标值与价值网络估计值的差值，以该差值作为数据元组的优先度[23].相比于1 步时间差分误差，N步时间差分误差具有更小的估计偏差，但同时也增加了后续推演的计算量，增大了算法的复杂度.

1.3 重要性采样机制

重要性采样是通过给样本添加重要性系数，修正因偏好采样产生的训练偏差.优先经验回放中的优先采样，尽管是从完整数据集中采集样本，但因偏好优先度高的数据，易造成神经网络梯度更新偏向于优先度高的数据集，带来训练偏差.为此，很多算法采用了重要性采样来修正该训练偏差.鉴于本文赋予数据元组的初始优先度为1，且随着训练步数增长不断降低优先度，数据元组相对应的重要性权重也应遵循随训练步数增大逐渐递减的变化规律.重要性采样在强化学习算法中应用广泛，置信域策略优化[24]（Trust region policy optimization，TRPO）为随机策略更新添加了一个置信域，通过KL 散度（Kullback-Leibler divergence）惩罚来约束梯度更新，保证了梯度的正向更新.近端策略优化[25]（Proximal policy optimization，PPO）则是计算新策略与旧策略的重要性比率，以此衡量新策略与旧策略的差异，通过设置截断比率的范围值，约束新策略的梯度正向更新.

2 离线强化学习方法

2.1 强化学习

强化学习通常被表示为马尔科夫决策过程[22]（Markov decision process， MDP） ，M=(S,A,P,R,p0,γ,H) ， 其中st∈S表 示状态空间，at∈A表示动作空 间，P:st+1～P(·|st,at)表 示 状 态 转 移 概 率 函 数，R:rt=R(st,at) 表 示奖励函数，p0表示初始状态分布， γ表示折扣因子，H表示任务的尺度，一般是指片段环境中一个片段的固定步数，st，at，p0，rt分别表示t时刻的状态、动作、0 时刻的状态转移概率和t时刻的奖励.强化学习的目标是使用经验来学习一个行动策略 π:S→A，以最大化累积折扣期望奖励：其中s0～p0，Eπ表示当使用策略 π时的累积折扣期望奖励，J(π)表示关于策略 π的目标函数，并且对于每个时间步t，都有at～π(·|st)，st+1～P(·|st,at) ， 且rt=R(st,at).每个策略 π都有一个相对应的Q 值函数Qπ(st,at)=Eπ[Rt|st,at]， 表示在状态st采取动作at后，执行策略π所获得的奖励期望.Q 值函数可通过如下贝尔曼算子得到：

其中， Tπ表示贝尔曼算子.Q 学习（Q-learning）[26]是通过迭代使用贝尔曼算子Qk+1=TπQk，直至Qk收敛到Qπ, 之后通过贪婪动作选择获取最优值函数Q*(st,at)=maxπQπ(st,at)所对应的最优策略，其中Q*(st,at) 表 示在状态st采取动作at的最优Q 值.DQN 是在Q 学习基础上，使用深度网络表示连续状态空间或巨大动作空间所对应的值函数，按照如公式（1）所示的计算方法，以值迭代的方式更新网络参数，获取最优价值函数[27].DQN 通过最小化如下目标实现值函数的更新：

其中， ϕ表示价值网络参数， ϕ′表示延迟更新的价值网络参数.

2.2 保守Q 估计离线强化学习方法

保守Q 估计离线强化学习方法（CQL）是通过在SAC 算法的基础上，为Q 值估计网络添加一个保守约束项，惩罚Q 函数对分布外数据的乐观估计.SAC 算法的策略评估通过最小化软贝尔曼残差来更新价值函数网络的参数：

其中， α是温度系数，正则项 logπ(at|st)鼓励策略进行探索和增强对噪声的鲁棒性.SAC 算法的策略提升则是通过最小化策略 π(·|s)和一个基于价值网络Q(st,π(st))的波兹曼分布之间的KL 散度来实现的，策略网络的目标函数表示如下：

其 中， Q(st,·) 表 示 基 于 能 量 的 策 略，Q(st,·)∝D表示数据集分布，DKL表示KL 散度.CQL 的通用目标函数如下：

其中， µ(at|st)是用来近似可以最大化当前Q 值函数迭代的策略， Bπk表示策略 πk对应的贝尔曼算子，(st,at) 表 示目标Q 值函数，(at|st)表示某个近似 µ(at|st) 的 策略， R(µ) 表 示约束 µ(at|st)和上一次迭代的策略分布的正则项.如果选择 R(µ) 为µ(at|st)和上一次迭代的策略的KL 散度，且假设上一次的策略分布为标准分布，则CQL 的目标可以定义为：

从CQL 的目标函数可以看出，其是对数据集中的样本进行价值函数的乐观估计，而对数据集之外的数据进行保守估计，通过惩罚项为真正的Q 值函数估计设定一个下界，防止其在分布外数据上的过高估计.

2.3 优先经验回放机制

经验回放是离策略强化学习中的重要机制.智能体通过从存放有历史数据的经验回放池中标准采样，既打破了数据间的时序依赖关系，使得输入神经网络的数据符合独立同分布的特性，又能利用历史数据更新当前网络参数，提升数据利用率.然而，经验数据的价值不一，对所有经验数据采取等价采样概率的标准采样，忽略了数据本身的价值特性.为此，PER 提出使用时间差分误差（TDerror）作为数据元组的优先度度量指标，并依据优先度进行采样，进而更新神经网络参数.时间差分误差的定义如下：

其中， ϕ 和 ϕ′表示Q网络参数.在实际应用中，通常使用 |δ|作为优先度度量，并通过如下公式计算最终的采样概率：

其中N表示数据量，i表示数据的序号， ϵ ＞0表示一个小数值的常量，用以保证即使在 |δ(i)|为0的情况下，其对应的数据元组的采样概率pi始终为正.但优先经验回放会因采样偏好而引起样本偏差，通常把重要性采样作为优先采样数据的梯度更新系数来修正该偏差：

其中 β ∈[0,1]， 当 β=0 时 ，wi=1，表示重要度为1，即不对采样的数据进行修正，完全按照优先采样的数据更新网络梯度；当 β=1 时 ，wi=即使用wi对优先采样的数据进行修正.实际应用中，本文设置 β的初始值为1，使用线性退化机制，随着训练进行逐渐降低 β的值直至为0.即在训练初始阶段，加大对数据的修正值，随着训练进行，网络参数更新趋于稳定，减小修正直至不再进行修正.

3 基 于 时 间 差 分 误 差 的 离 线 强 化 学 习 采样方法

3.1 高效样本采样方法

本文提出一种新的离线强化学习智能体采样策略，在训练初期采用优先采样策略对高价值数据进行优先偏好采样，之后采用标准采样策略对数据进行无偏采样.优先采样策略的执行步数区间，按照不同任务特点，以超参数的形式设定.根据实验经验，一般在整个训练过程的前 1/5至1/3步数之前使用优先经验回放，之后再使用标准采样策略.为此，本文为智能体分别建立2 个经验回放池：优先经验回放池和标准经验回放池.为保证离线数据集完整性，两个经验回放池的大小相同，初始化数据一致.优先经验回放池中的数据初始优先度均设置为1，以保证采样时对新数据的优先探索.与以往方法类似，本文采用时间差分误差作为数据元组的优先度度量，同时采用重要性采样来纠正因优先采样引起的训练偏差.除在训练不同阶段使用不同的采样策略外，算法其余部分包括超参数设置均保持一致.本文使用CQL 作为基础离线强化学习算法.本文的算法整体结构如图1 所示.

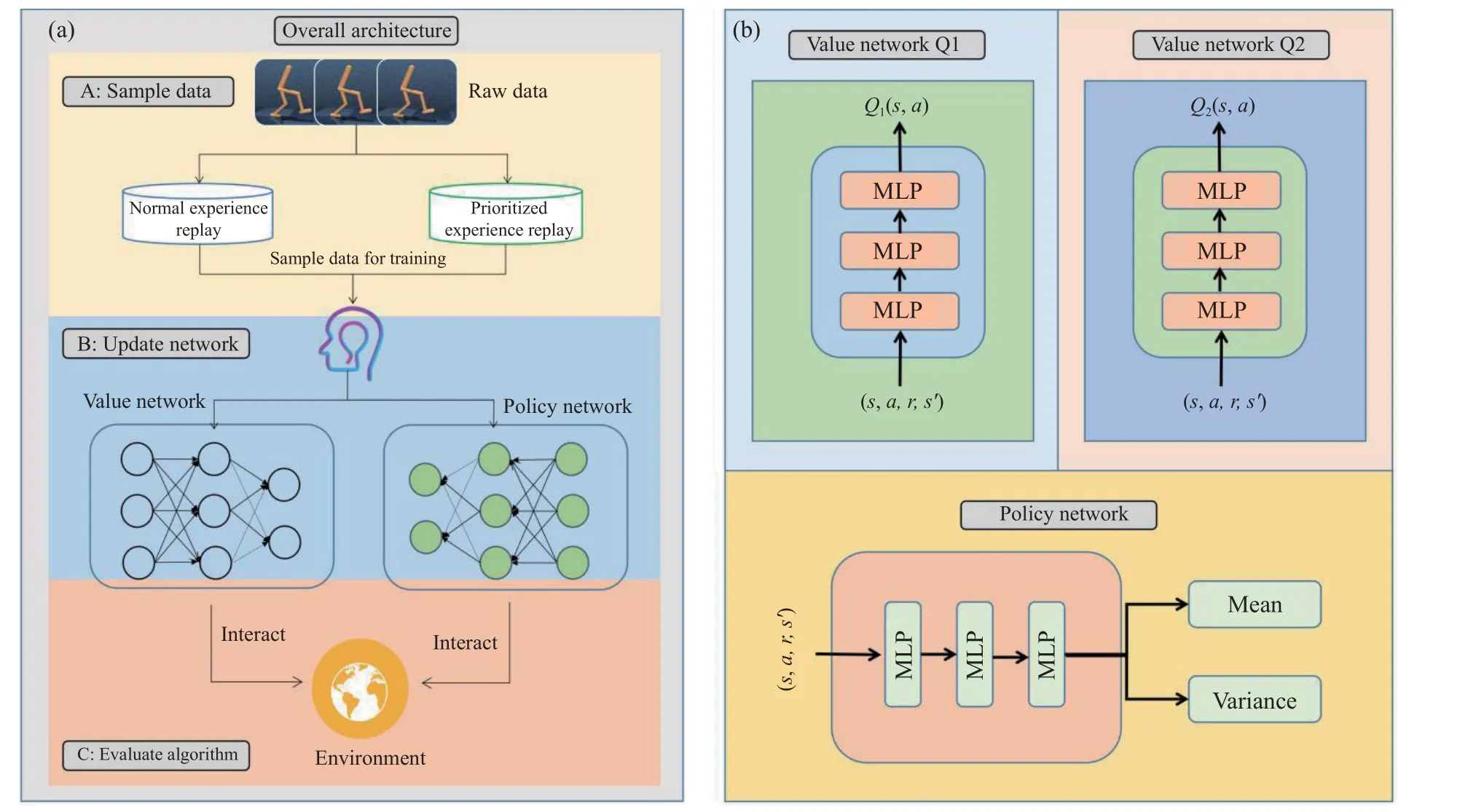
图1 本文方法的框架和网络的具体架构.(a) 本文方法的框架; (b) 网络的具体架构Fig.1 Framework of the method and the specific architecture of the network in this paper: (a) framework of the method in this paper; (b) the specific architecture of the network

如图1 所示，图1（a）中包括了本文提出的方法的3 个步骤：数据采样、网络更新和算法评估，其中数据采样部分包括2 个经验回放池，智能体从2 个经验回放池中采集训练样本；网络更新部分是指利用采样的数据进行算法的离线策略学习；算法评估部分是指对学习的智能体在实际环境中进行性能评估.（b）本文的算法主要涉及策略网络和价值网络的训练.本文采用双价值网络架构，鉴于本文实验环境中的任务都是连续动作空间，本文假设动作服从高斯分布，策略网络的输出为动作分布的均值和方差，最终的动作通过在策略网络的分布中采样得到.

3.2 多种类时间差分误差度量

正如本文在2.2 章节中的介绍，强化学习算法通常使用时间差分误差来衡量当前策略和价值函数，并据此对策略和价值函数进行更新.PER 等使用时间差分误差作为样本优先度度量均取得较好性能，结合计算复杂度考量，本文的方法采用1 步时间差分误差作为优先经验回放的优先度度量.根据时间差分误差计算公式(8)可知，时间差分误差取决于目标Q 值函数Qϕ′(st+1,at+1).本文的双Q 价值网络采用3 种计算目标Q 值的方法：

最小化的双Q 值网络：使用双目标Q 值网络的最小值作为Q 值网络的目标值.

最大化的双Q 值网络：使用双Q 值目标网络的最大值作为Q 值网络的目标值.

凸组合的双Q 值网络：使用两个目标Q 值网络的凸组合作为Q 值网络的目标值.

其中 λ ∈(0,1)是温度系数，表示凸组合中最小化的双Q 值的权重，j表示网络的序号.可以看出，最小化和最大化的双Q 值是凸组合的双Q 价值网络的特殊形式，分别代表 λ=1 和 λ=0时的凸组合的双Q 值.当目标Q 值确定后，本文方法中的时间差分误差可表示为：

其中， δ(st,at)表示数据 (st,at) 的时间差分误差，Qtarget(st,at) 表 示Qtargetmin(st,at)，Qtargetmax(st,at)和Qtargetcomb(st,at)共3 种计算目标Q 值方式之一.与公式(9)类似，基于时间差分误差的样本优先度如下：

其中，p(st,at)表示数据 (st,at) 的 样本优先度， ϵ ＞0保证每个数据元组都有被采样的可能性.本文的方法也使用了重要性采样，但与PER 不同的是，本文只在计算样本优先度p(st,at)时使用了重要性采样，在梯度更新时，则并未使用.实验结果表明，本文这种改动并未影响实验效果.本文的方法中的策略网络与CQL 中的策略网络更新方法一致：

其中， η为策略网络的更新步长， θ 为策略 π的参数.本文的算法伪代码如下：

算法1：基于时间差分误差的离线强化学习采样方法（CQL版本）初始化：双Q值网络 ， ，双Q值目标网络 ， ，策略网络 ，Q值网络更新步长 ，策略网络 的参数更新步长 ，片段长度为 ，批处理大小为 ，初始优先度设置为1，最大训练步数 ，优先采样的最大步数 ，标准经验回放池 ，优先经验回放池 ，Q网络参数 的梯度 ，Q网络参数 的更新步长 ，数据序号，目标Q值网络参数软更新系数.t ＜T Qφ1 Qφ2 Qφ′1 Qφ′2 πθ τ πθ η H N T Tp B Bp φ Δ φ ζ i τ对于训练步数 ：t ＜Tp 如果 （即从优先经验池中采样）：1.据公式(15)计算优先采样率并从优先经验池中采样 个批处理数据wi=(N·P(i))-β/maxiwi 2.算重要性采样权重：N 3.据公式 (11)、(12)或(13)估计Q目标值Qtarget(st,at)4.算Q值网络梯度变化Δ ←Δ+δi·∇ϕ[(E(st,at)～D[Qφ(st,at)]-Qtarget(st,at))2]5.新Q值网络：φ ←φ+ζ· Δ φ′←τφ+(1-τ)φ′6.更新目标Q值网络：7.据公式(16)更新策略网络#否则（即从标准经验池中采样）：8.根据公式 (11)、(12)或(13)估计Q目标值Qtarget(st,at)9.计算Q值网络梯度变化Δ ←Δ+∇φ[(E(st,at)～D[Qφ(st,at)]-Qtarget(st,at))2]10.更新Q值网络：φ ←φ+ζ· Δ φ′←τφ+(1-τ)φ′11.软更新目标Q值网络：12.根据公式(16)更新策略网络

4 基 于 时 间 差 分 误 差 的 离 线 强 化 学 习 采样方法的实验验证

4.1 实验设置

本文在离线强化学习公测数据集D4RL 上进行实验.D4RL 是DeepMind 公司开发的一套仿真模拟数据集，包括机器人、迷宫、自动驾驶等多种任务下的数据.每种任务分别使用随机策略、中等策略、中等回放、中等—专家策略生成4 种数据集，不同策略生成的数据质量不同，这些生成数据的策略被称为行动策略（Behavior policy）.每个数据集有约1000000 或2000000 个 (s,a,r,s′,done)数据元组，其中 done为一个片段（episode）的结束标志.本文的实验是在D4RL 中的Hopper（图2（a））、Half-Cheetah（图2（b））和Walker2d（图2（c））3 种任务的数据集上进行训练，在对应的DMControl 实际环境中进行验证，这3 种任务分别对应不同维度的连续状态空间和动作空间.本文在实验中使用3 种任务相对应的随机策略、中等策略和中等—专家策略生成的9 个数据集，具体如表1 所示.

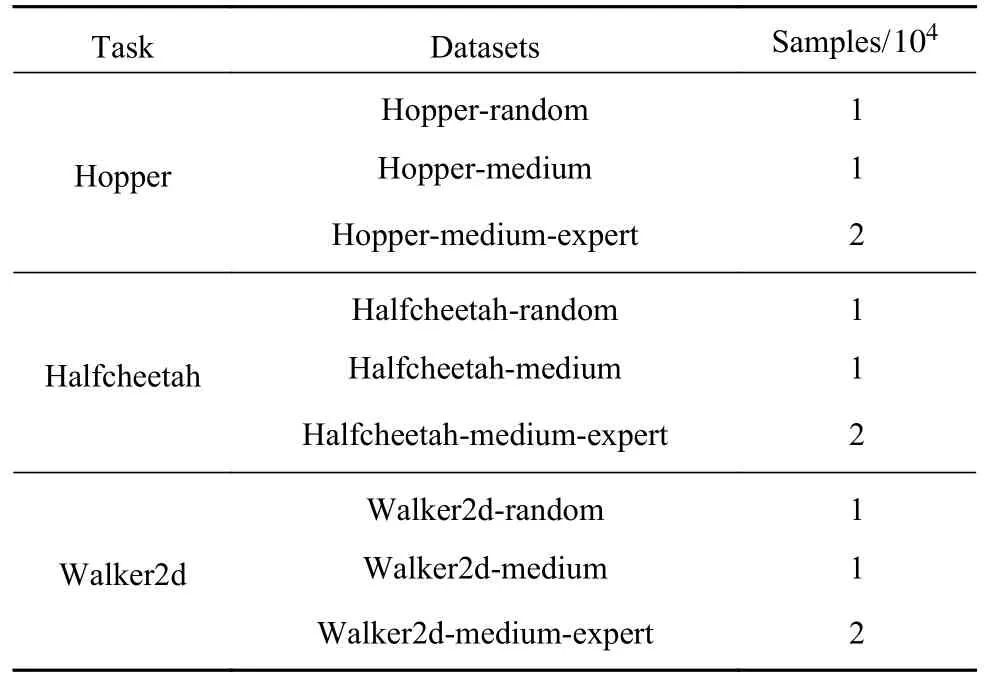
表1 实验所用的D4RL 数据集Table 1 D4RL dataset used in our experiment

图2 本文实验所使用的DMControl 中的3 个仿真环境.（a） Hopper；（b） HalfCheetah；（c） Walker2dFig.2 The three simulation environments in DMControl used for the experiments in this paper: (a) Hopper; (b) HalfCheetah; (c) Walker2d

4.2 主要实验

为验证本文方法的性能，本文利用上述提到的数据来训练智能体，并和已有的结合采样机制的离线强化学习算法进行比较.设置训练总步数为1000000 步，优先经验采样的步数为200000，之后的训练从标准经验回放中标准采样.为公平比较，本文在所有的实验中均使用相同的超参数.算法评估是通过智能体与DMControl 中相对应的环境交互实现的，每5000 步进行一次评估.每个任务共评估10 次，每次评估执行1000 步，以1000 步的累积奖励值作为当次评估的值，以10 次评估的平均值作为最终的评估值.本文采用最小化双Q 值作为本次实验的3 种算法的目标Q 值.本次实验主要涉及3 种算法：（a）CQL_PER 算法：表示使用优先采样方式进行样本采样的CQL 算法，该方法为常用的结合采样策略的离线强化学习方法之一；（b）CQL_H 算法：本文提出的方法，表示使用标准采样和优先采样相结合的方式进行样本采集的CQL 算法；（c）CQL_PER_N_return：表示使用N步返回计算样本优先度并使用优先采样方式进行样本采集的CQL 算法，该方法为常用的结合采样策略的离线强化学习方法之一.

如图3 所示，主要实验部分是对CQL_PER、CQL_H(本文的方法)和CQL_PER_N_return 这3 种方法在DMControl 仿真控制平台上的Hopper（图3（a））、HalfCheetah（图3（b））和Walker2d（图3（c））这3 种环境中进行了性能测试.其中，横轴表示不同质量的数据类型（Data types），纵轴表示片段奖励值（Episode return），柱状图中的红色误差棒表示算法性能的方差.

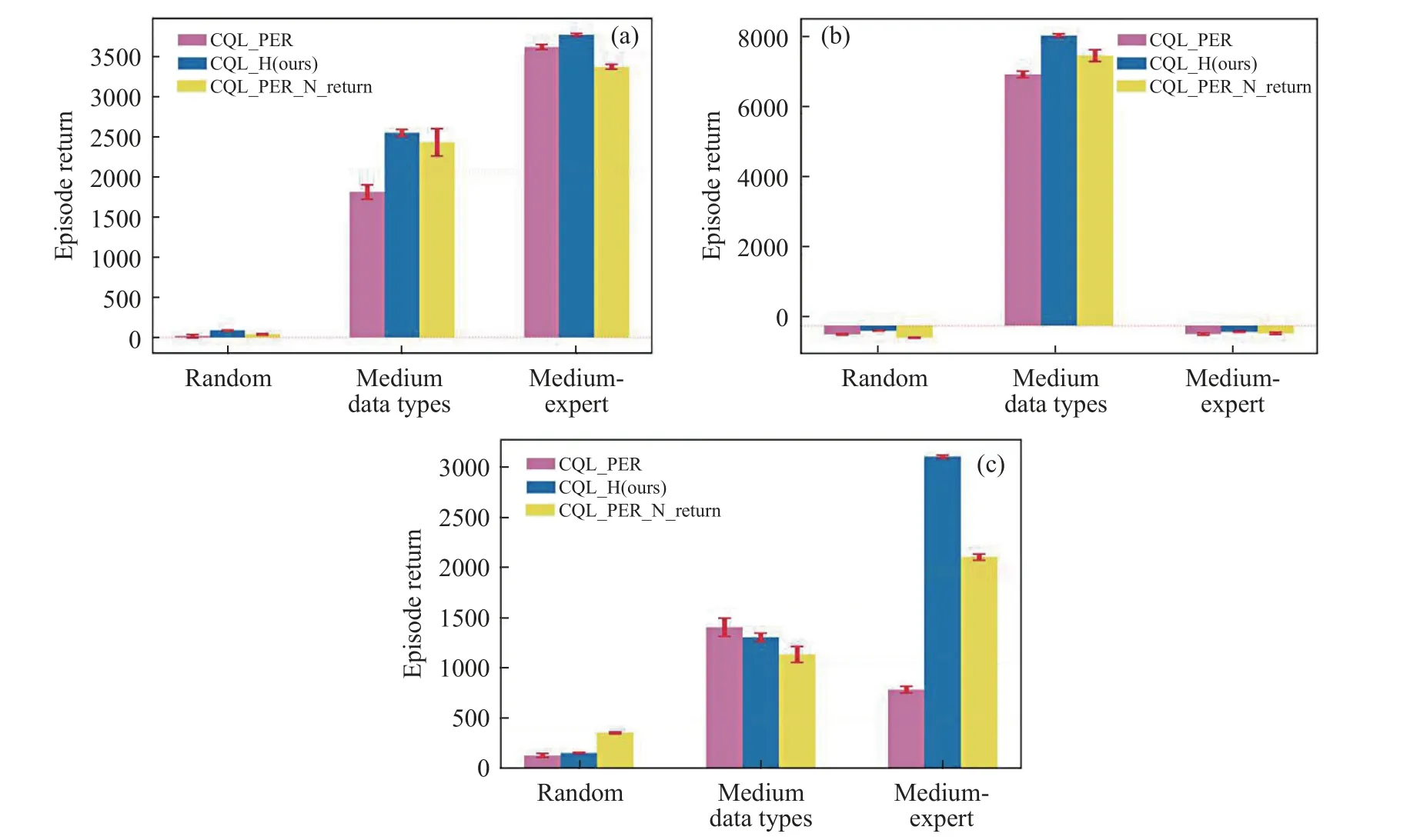
图3 本文的方法CQL_H 与CQL_PER、CQL_PER_N_return 算法在3 种环境的3 类数据上的性能比较.（a） Hopper; （b） HalfCheetah; （c） Walker2dFig.3 The performance of the methods CQL_H and CQL_PER, CQL_PER_N_return algorithms in this paper is compared on three types of data for three environments: (a) Hopper; (b) HalfCheetah; (c) Walker2d

按照实验设定，本文针对3 种任务上的random、medium 和medium-expert 3 类数据，分别使用3 种离线强化学习方法进行了策略训练.由图3可知，在进行1000000 步的网络梯度更新后，CQL_H 在Hopper、HalfCheetah 中的3 类数据上的策略的最终性能均优于CQL_PER 和CQL_PER_N_return.在Hopper 环境中，CQL_H 在medium 数据集的最终性能超过CQL_PER 约40.6%，超过CQL_PER_N_return 约4.9%；在medium-expert 数据集上的最终性能超过CQL_PER 约4.2%，超过CQL_PER_N_return 约11.2%；在HalfCheetah 环境中，CQL_H 在medium 数据集上的最终性能超过CQL_PER 约15.5%，超过CQL_PER_N_return 约7.5%；而在Walker2d 中的medium 数 据集上，CQL_PER 的效果反而相对而言更优，这可能是因为Walker2d 的medium 数据集更易于策略进行优先采样.

此外，图3 也展示了3 种算法在不同环境不同类型数据集上的性能的方差，可以看出，CQL_H相比于其他2 种方法，在大部分环境中具有最小的误差，表明使用CQL_H 学习到的策略性能更为稳定.

4.3 消融实验

下面针对CQL_H 开展消融实验，主要分为2 部分：

（1）CQL_H 使用标准采样和优先采样相组合的采样方式，将使用该采样方式与单独使用标准采样方法和单独使用优先采样方法的性能进行比较.（2）采用3 种时间差分优先度时，CQL_H 对应3 种不同的算法，研究在相同的仿真环境下，不同优先度的算法对算法性能的影响.

在消融实验（1）中，本次实验使用500000 步的训练次数，即对网络参数更新500000 次.与主要实验的设置一致，为缓解训练偏差，本文每1000 步进行一次评估.每个任务共评估10 次，每次评估执行1000 步，以1000 步的累积奖励值作为当次评估的值，使用10 次训练的均值和方差作为最终的均值和方差，每次训练均使用随机种子.本实验对CQL_H 和CQL_Uniform、CQL_Priority 进行性能对比，这3 种算法分别是：(a)CQL_H，本文的方法，表示使用标准采样策略和优先采样策略的CQL_H 算法；(b)CQL_Uniform，表示完全使用标准采样的策略的CQL_H 算法；(c)CQL_Priority，表示完全使用优先采样策略的CQL_H 算法，其中优先采样中的优先度度量使用最小化双Q 值的时间差分误差.

如图4 所示，本文对CQL_Uniform、CQL_H(本文的方法)和CQL_Priority 这3 种方法在Hopper（图4（a） ） 、 HalfCheetah（图4（b） ） 和Walker2d（图4（c））这3 种环境中进行了性能测试.

图4 本文的方法CQL_H 使用不同采样方式在3 种环境的3 类数据上的性能比较.（a） Hopper; （b） HalfCheetah; （c） Walker2dFig.4 The performance of the method CQL_H using different sampling methods in this paper is compared on 3 types of data for a total of 3 environments: (a) Hopper; (b) HalfCheetah; (c) Walker2d

从图中可知，在进行500000 步的网络梯度更新后，CQL_H 在Hopper、HalfCheetah 中的3 类数据上的策略的最终性能都优于CQL_Uniform 和CQL_Priority.在Hopper 环境中，CQL_H 在medium 数据集的最终性能超过CQL_Uniform 约10.4%，超过CQL_Priority 约7.3%；在medium-expert 数据集上的最终性能超过CQL_Uniform 约 11.8%，超过CQL_Priority 约17.2%；在HalfCheetah 环境中，CQL_H 在medium 数据集上的最终性能超过CQL_Uniform 约43.9%，超过CQL_Priority 约14.7%.而在Walker2d 中的medium 数据集上，CQL_Priority 的效果相对而言更优，这与主要实验中的结果一致，即Walker2d 数据集更适合使用优先采样的采样方式训练策略.

从图4 中的误差棒也可看出，CQL_H 相比于其他2 种方法，在大部分环境中具有最小的性能方差，这也反映出使用标准采样和优先采样组合的采样方式的CQL_H 算法相比于仅使用标准采样的CQL_Uniform 算法和仅使用优先采样的CQL_Priority 算法，策略稳定性更强.

在消融实验（2）中，本文采用3 种基于双Q 值网络目标值的时间差分误差，分别利用最小化双Q 网络值、最大化双Q 网络值和凸组合的双Q 网络值计算得到.基于3 种时间差分误差，本文采用3 种不同的优先采样策略，从优先经验回放池中采集训练数据.除了目标Q 值计算方式不同，3 种算法的网络结构和其余的超参数均设置一致.鉴于计算资源有限，本文只在Hopper-medium, HalfCheetah-medium,Walker2d-medium 这3 种任务上进行训练和评估.本次训练和评估的设置和上文中的介绍相同.和BCQ 算法一致，本文将凸组合的双Q 网络值的计算公式(13)中的调节因子超参数λ设置为0.75.3 种算法分别为：（a）CQL_H_min，表示以双Q 值估计的最小值计算时间差分误差，以此作为CQL_H 算法中优先经验采样策略部分的优先度度量，是相对而言更为悲观的优先度度量方式，也是本文中的CQL_H 默认形式；(b)CQL_H_max，表示以双Q 值估计的最大值计算时间差分误差，以此作为CQL_H 算法中优先经验采样策略部分的优先度度量，是相对而言更为乐观的优先度度量方式；(c)CQL_H_medium_0.75，表示以双Q 值估计的最大、最小值的凸优化组合计算时间差分误差，以此作为CQL_H 算法中优先经验采样策略部分的优先度度量，是比较中庸的优先度度量方式.其中0.75 表示最小化双Q 值的温度系数.

如图5 所示，本次实验是对使用不同方式计算的时间差分误差的CQL_H 算法的性能进行验证，以比较不同计算方式的时间差分对算法的性能有何不同影响.图中的曲线表示评估值均值，阴影部分表示评估值的方差.可以看出，CQL_H_min 在3 个环境中相比CQL_H_max 和CQL_H_medium_0.75 具有更好的数据利用率和最终性能.在Hopper-medium（图5（a））环境中，CQL_H_min 在250000训练步即达到了3000 左右，但随即又下降，直至最终和CQL_H_max、CQL_H_medium_0.75 收敛至2000.在HalfCheetah-medium（图5（b））环境中，CQL_H_min 在200000 训练步即达到了7400，在后续的训练中稳定在5000 至7500，而CQL_H_max、CQL_H_medium_0.75 则未能学习到有效策略，网络一直未收敛.在Walker2d-medium（图5（c））环境中，CQL_H_min 在250000 训练步后逐步稳定，最终收敛在1500 附近.CQL_H_max 则收敛在200 附近，而CQL_H_medium_0.75 则未能学习到有效策略，策略网络未收敛.从图中可以看出，本文的3 种方法在Hopper-medium 上性能较好，但CQL_H_max 和CQL_H_medium_0.75 在HalfCheetah-medium, Walker2d-medium 上性能较差，CQL_H_min 在3 种任务上均表现较好.

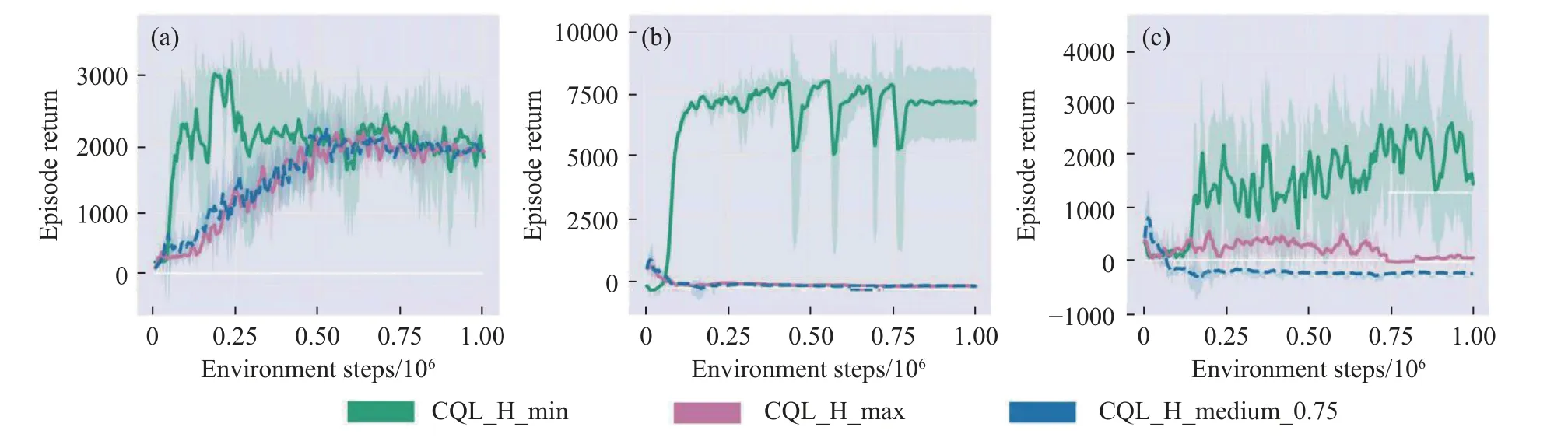
图5 本文的方法CQL_H 使用3 种时间差分误差的优先采样策略的性能比较.（a） Hopper-medium; （b） HalfCheetah-medium; （c） Walker2d-mediumFig.5 Comparison of CQL_H with three different TD-error: (a) Hopper-medium; (b) HalfCheetah-medium; (c) Walker2d-medium

从图5 中代表策略方差值的阴影部分可知，尽管CQL_H_min 在数据利用率和最终性能上具有较大优势，但策略在部分训练环节的方差较大.

5 结论

本文围绕离线强化学习数据利用率低、易加剧外推误差的问题，提出一种新的结合优先采样策略和标准采样策略的离线强化学习采样策略，通过设立2 个经验回放池，在训练初期从优先经验回放池中优先采样，之后从标准经验回放池中标准采样，并使用双Q 价值网络计算的时间差分误差作为优先度度量，可与任何基于Q 值估计的离线强化学习算法相结合.在D4RL 上的实验表明，本文的方法相比于已有的结合采样机制的基于CQL 的离线强化学习算法，具有更优的样本利用率和最终性能，较好地缓解了外推误差问题，且训练过程更稳定.消融实验表明，优先采样和标准采样相结合的采样方式对算法至关重要，此外，与最大化双Q 值和凸组合的双Q 值相比较，使用最小化双Q 值目标估计的时间差分误差更适合作为优先采样度量.本文的方法是从采样策略的角度研究离线强化学习算法，与之前的研究相比，无需调整算法的基本架构和网络的基本结构，最大限度避免增加网络参数，实现简单，可扩展性强.本文的研究旨在提升数据利用率，克服离线强化学习外推误差问题，为解决数据采集难、样本数据有限、质量不一的控制决策任务，提供了新的研究思路和方法支撑，有助于相关研究者探索高效、安全、鲁棒的离线强化学习算法，进一步推动强化学习在复杂实际场景中的落地应用.