基底不均匀沉降对隧道结构力学特性的影响研究*

颜溧洲

(中大桥勘测设计院集团有限公司,湖北 武汉 430050)

1 工程概况

1.1 隧道概况

拟建隧道是一座下穿高速公路匝道隧道,项目道路等级是高速公路,设计速度为60 km/h,为单向双车道.下穿隧道孔净宽12.5 m,净高7.3 m,底板厚1.1 m,顶板厚1.0 m,侧墙厚1.0 m.隧道沿着山坡建设,隧道基底一半坐落于现状坡体,一半处于填方区,隧道建成后,顶部将修建一条高速公路,如图1所示.由于项目施工进度调整,在建设隧道之前,场地已被整平,整平标高高于隧道基底约3 m.故隧道施工时,需重新开挖深约3 m的基坑.

图1 下穿隧道横断面示意图

1.2 地质概况

根据地勘报告,隧道下方地层自上而下分别为粉质黏土、全风化花岗岩以及砂砾状强风化黄岗岩,具体参数详见下表1.

表1 各地层主要物理力学指标

2 基底沉降和隧道结构受力计算

2.1 计算荷载分类及取值

1)结构自重按结构的实际质量计,钢筋砼容重取25 kN/m3,路面层取23 kN/m3.

2)地面超载按20 kPa考虑.

3)施工荷载,按23 kPa考虑.

4)其他荷载均按相关规范的有关规定计算,如表2所示.

表2 荷载分类表

2.2 基底不均匀沉降计算

根据施工现场反馈,隧道施工前原场地已回填至隧道基底以上约3.0 m,回填时间约一年半,故项目场地既有土层又有回填土,在填土自重和场地施工作用下会产生一定的固结沉降.故计算隧道基底工后的不均匀沉降对隧道结构受力的影响需扣除此部分沉降.利用MIDAS-GTS建立二维有限元模型,隧道结构采用梁板单元,土层采用面单元,如图2所示,软件计算基底的工后沉降需考虑以下三步.

没有什么值得敬服之处的苏州园林，毫无“月落乌啼”诗意的寒山寺，这些现实击碎了芥川脑海里由古诗词所构建的浪漫唯美的中国形象，作为“中国趣味的爱好者”，当他来到中国，发现现实中的中国与古诗词中的中国之间的反差时，失望之情溢于言表。

图2 有限元模型

1)步骤一:计算场地整平一年半时间内隧道基底标高处的沉降.由有限元计算得左侧墙对应基底位置沉降为3.4 mm,右侧墙对应基底位置沉降为35 mm,如图3所示.

图3 场地整平

2)步骤二:隧道基坑开挖,基底土体卸荷,坑底会产生向上隆起的回弹变形.此时,左侧墙对应基底位置沉降为0.6 mm,右侧墙对应基底位置沉降为30.1 mm,如图4所示,与步骤一沉降相比,开挖后基底明显向上隆起.

步骤二结束后,计算软件需进行位移清零处理,即步骤一与步骤二基底沉降和隆起不会作用在隧道结构上.

图4 基坑开挖

3)步骤三:隧道主体结构、内部铺装、两侧及顶部填土均已施工完成,隧道及隧道顶部的高速路处于运营通车状态.此刻,左侧墙对应基底位置沉降为20.9 mm,右侧墙对应基底位置沉降为42.1 mm,如图5所示,即为隧道及顶部公路建成后的基底工后沉降数值.

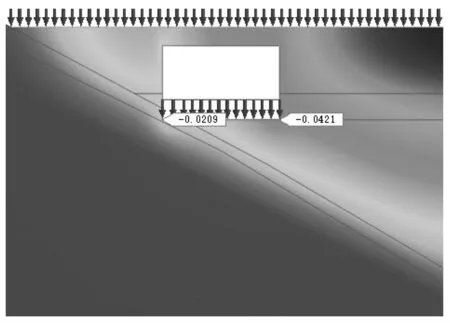
图5 基底工后沉降

2.3 基底不均与沉降对结构受力的影响

根据文献搜集,现阶段基底不均匀沉降作用在隧道结构上的力学计算暂无统一标准.根据工程经验,本文提出强制位移法和调整基床系数法来定量计算隧道结构受力情况.

1)计算模型

将下穿隧道作为主要横向受力的框架结构,计算将采用单位长度建模,按施工与运营阶段可能出现的最不利荷载组合,进行结构强度、刚度计算.本文计算采用MIDAS-GTS有限元软件,底板及侧墙均采用受压的土弹簧模拟,如图6所示.

图6 结构计算模式

2)强制位移法

将2.2节步骤三的计算结果在计算模型中以强制位移的形式作用在隧道底板下的土弹簧上,即由左侧墙向右侧墙底施加线性递增强制位移,具体位移为0.020 9～0.042 1 m,如图7所示,计算结果如图8所示.

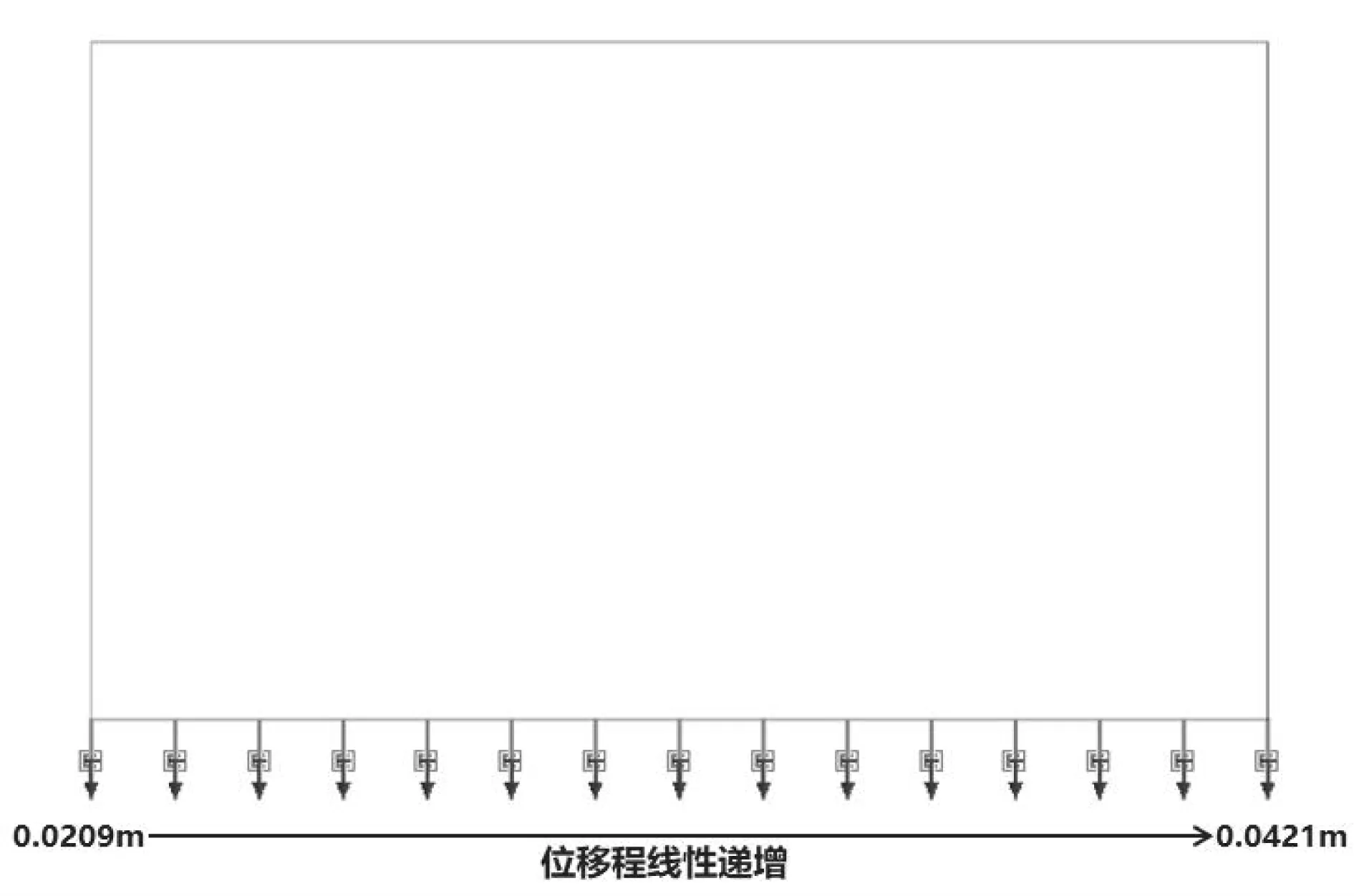
图7 强制位移法

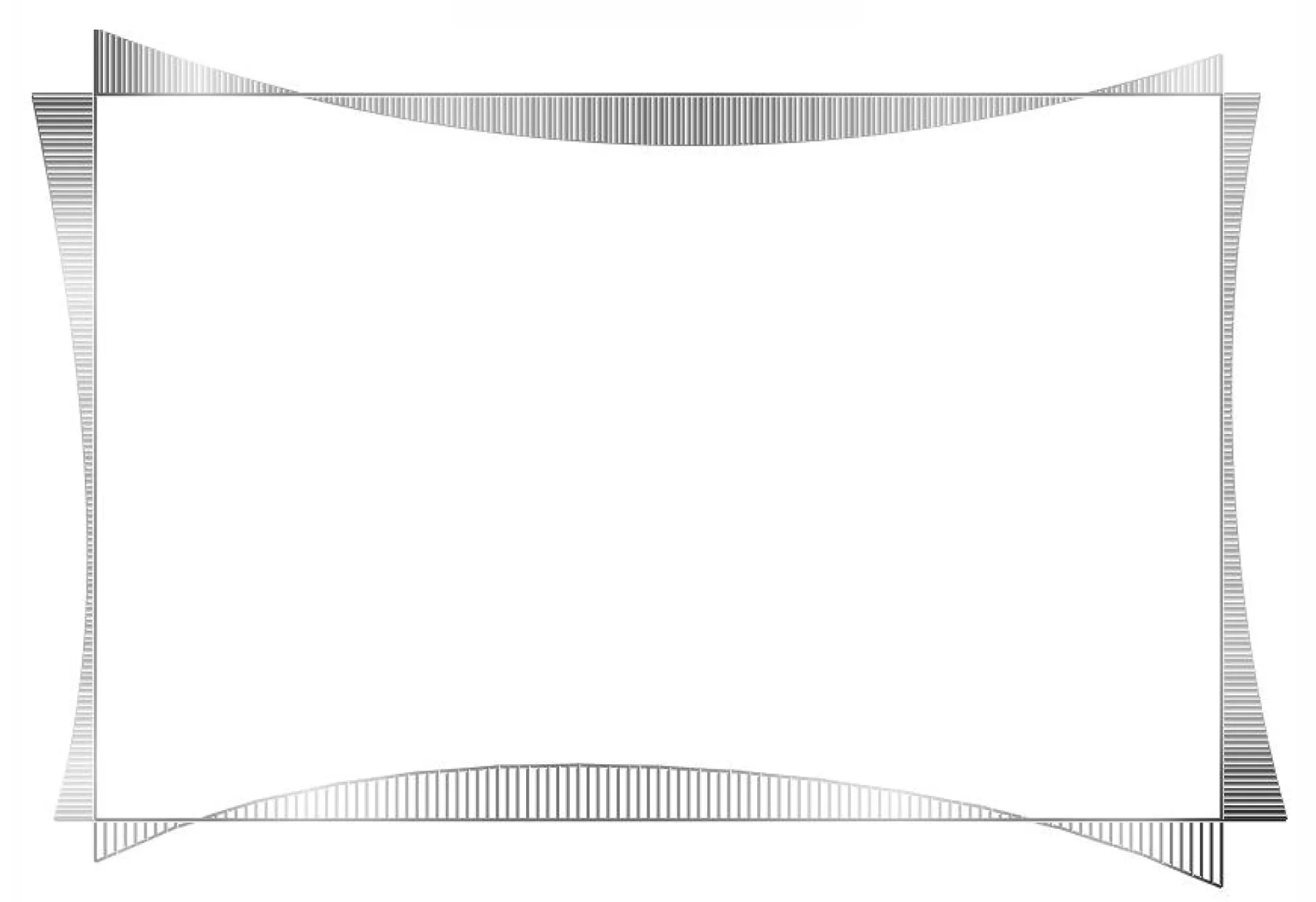
图8 弯矩图

计算结果取包络值,如表3所示,得到顶板跨中弯矩约为1 004 kN·m,顶板与侧墙支座处弯矩为1 311kN·m;底板跨中弯矩约为1 102 N·m,底板与侧墙支座处弯矩为1 355 N·m;侧墙跨中弯矩约为446 kN·m.

表3 配筋计算表

3)调整基床系数法

根据沉降计算结果和基底压力反算底板下土体的基床系数,将反算的基底土体基床系数输入模型计算.基床系数计算公式为:

Kv=p/s

(1)

式(1)中,p为基底压力,单位为kPa;s为p对应的沉降,单位为m;Kv为基床系数,单位kPa/m.

考虑隧道结构自重、隧道内部铺装、顶部覆土以及车辆荷载等,隧道基底压力约为135 kPa,故根据公式(1),底板左右两侧土体基床系数分别可计算得到,左侧为Kv1=135 kPa/0.020 9 m =6 459 kPa/m,右侧为Kv2=135 kPa/0.042 1 m= 32 06 kPa/m,将土体基床系数由左向右呈一次线形关系赋值,并进行弯矩计算,如图9所示,计算结果如图10所示.

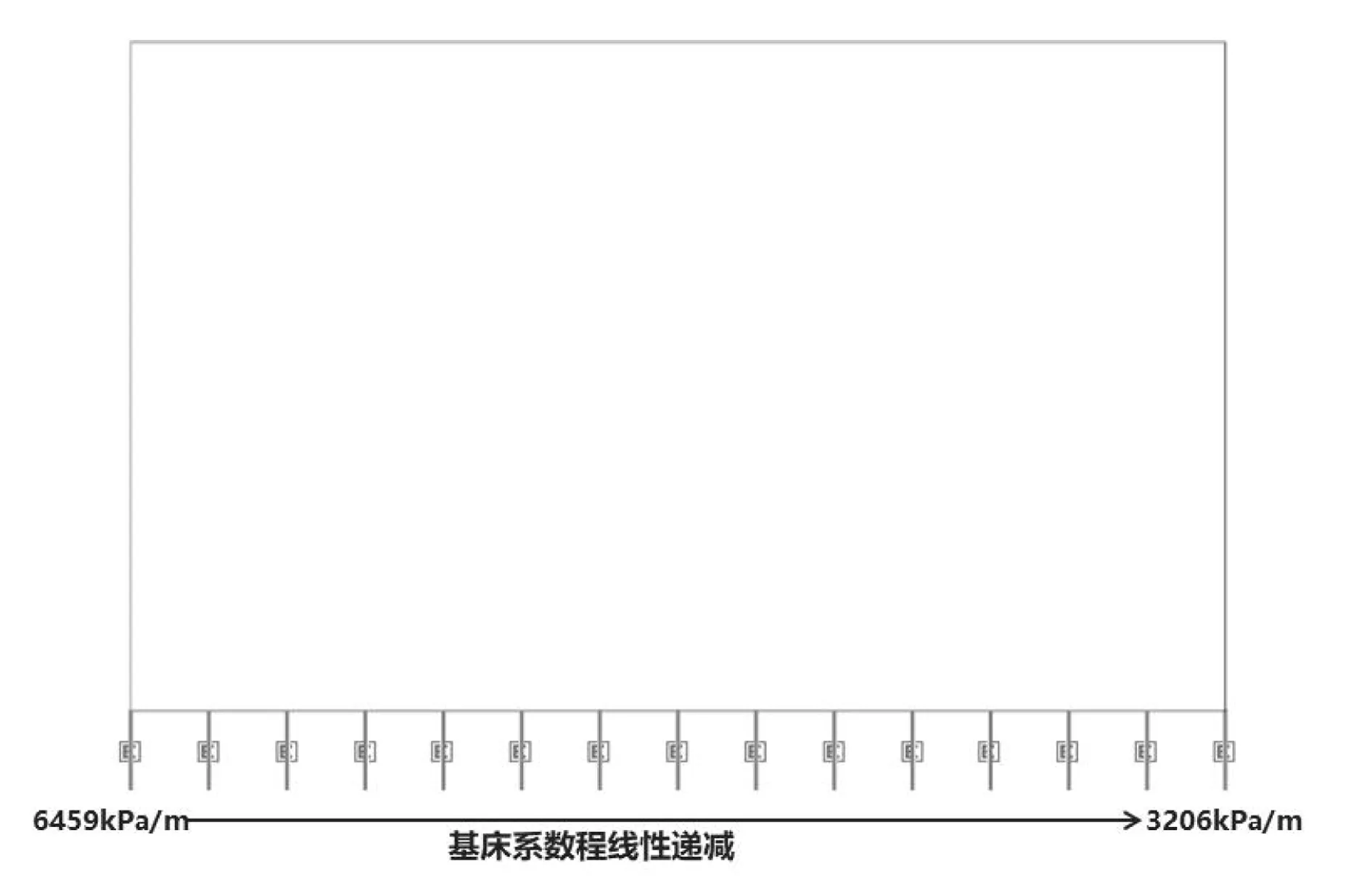
图9 调整基床系数法

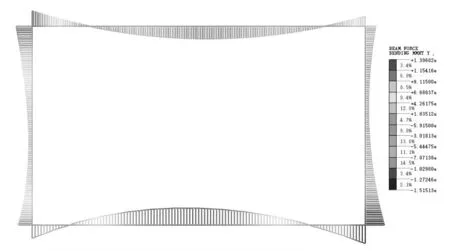
图10 弯矩图

计算结果取包络值,如表4所示,得到顶板跨中弯矩约为1 026 kN·m,顶板与侧墙支座处弯矩为1 260 kN·m;底板跨中弯矩约为1 515 N·m,底板与侧墙支座处弯矩为1 390 N·m;侧墙跨中弯矩约为540 kN·m.

表4 配筋计算表

4)未考虑不均匀沉降下的隧道结构受力

将上述计算模型中的强制位移取消,如表5所示,计算得到顶板跨中矩约为1 010 kN·m,顶板与侧墙支座处弯矩为1 044 kN·m;底板跨中弯矩约为1 093 N·m,底板与侧墙支座处弯矩为1 1 057 N·m;侧墙跨中弯矩约为465 kN·m,侧墙与顶板支座处弯矩为1 044 kN·m,侧墙与底板支座处弯矩为1 057 N·m,如图11所示.

图11 弯矩图

表5 配筋计算表

经对比分析图12和表6可知,与不考虑基底不均匀沉降影响相比,两种计算方法下隧道结构的弯矩均有一定增加,可见隧道结构基底的不均匀沉降明显会增加结构受力,影响结构的安全性.其中强制位移法主要对结构支座处弯矩影响较大,约增加25%～30%的弯矩,而调整基床系数法对结构各个部位均产生影响,顶板和侧墙上部弯矩仅增加不到10%,但是底板和侧墙支座处增加弯矩约43.42%,底板跨中增加弯矩约27.17%.

图12 弯矩对比

表6 弯矩对比表

经对比分析图13和表7可知,与不考虑基底不均匀沉降影响相比,强制位移法的计算结果显示:①顶板、底板、侧墙板边支点配筋增加约41.39%,设计时需考虑顶板、底板外侧配筋增加约41.39%;②顶板、底板和侧墙跨中配筋不增加,即设计时顶板、底板和侧墙内侧配筋不变.调整基床系数法计算结果显示:①顶板边支点和侧墙上支点筋增加约25.45%,底板边支点和侧墙下支点配筋增加约59.38%,即顶板外侧配筋增加约25.45%,侧墙和底板外侧配筋增加约59.38%;②顶板和侧墙跨中配筋不增加,底板跨中配筋增加约30.85%,即设计时顶板、侧墙内侧配筋不变,底板内侧配筋增加约30.85%.基于工程安全的考虑,本隧道工程的结构配筋按照两种计算方法的包络取值.

图13 配筋对比

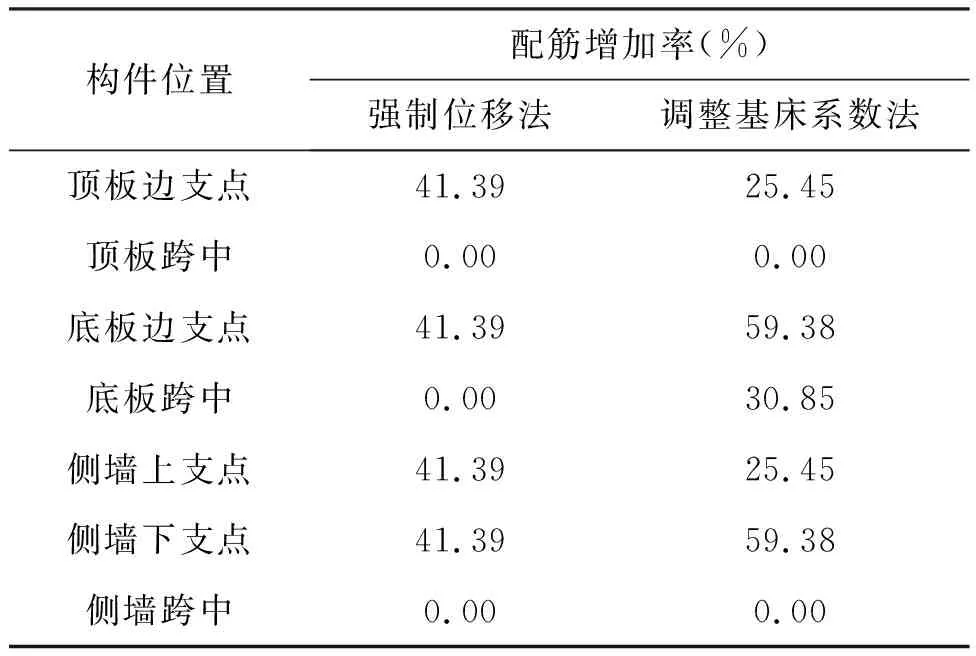
表7 配筋对比表

3 结论

1)经对比分析,强制位移法主要对隧道结构外侧受力筋影响较大,增加约41.39%的受力筋,对内侧受力筋几乎无影响;而调整基床系数法对隧道顶板和侧墙外侧受力筋影响较大,增加约25.45%的受力筋,对顶板和侧墙内侧受力筋几乎无影响,但是对底板内、外侧受力筋均产生较大影响,底板内侧增加约30.85%受力筋,底板外侧增加约59.38%受力筋.基于工程安全考虑,建议结构配筋按照两种方法的包络取值.

2)通过对比考虑与未考虑基底不均匀沉降两种情况下的结构受力,明显可以发现基底不均匀沉降对结构受力影响比较大,建议工程中应采取相应的地基处理,降低结构基底的不均匀沉降,以此优化结构配筋,节约工程造价.

3)由于地下工程的特殊性,计算模型和结构受力均属于理想状态,地基处理未必能做到完全消除不均匀沉降,建议结构配筋时考虑一定安全储备.

4)工程建成通车3年来,隧道结构裂缝正常,地面道路及明挖隧道总体变形满足使用要求,本文提出了强制位移法和调整基床系数法来模拟基底不均匀沉降对主体结构受力计算方法具有可行性,可以为同类工程提供计算参考,具有一定的借鉴意义.