基于IT2SFNN 的永磁同步电机加速自适应控制

肖凯文，李枫韵，李昊

（550025 贵州省 贵阳市 贵州大学 机械工程学院）

0 引言

近年来，永磁同步电机（PMSM）由于具有效率高、结构简单、制造成本低等优点，广泛应用于航天飞机、电动汽车、特种设备等领域[1-2]。永磁同步电机在实际应用中多数仍采用PID 控制，由于PID 算法比较简单，很难对多变量和强耦合的非线性PMSM 进行高精度控制。因此，提出更加有效的智能控制方案以解决系统中的混沌震荡和不确定参数问题是非常有必要的。

随着智能控制技术的不断提升，学者们提出很多强鲁棒性和抗干扰性的非线性控制策略，如自适应控制[3]、神经网络控制[4]、分数阶控制[9]等。游星星等[5]采用状态观测器对非线性系统不可测的状态参数进行模糊估计，保证了闭环系统输出信号的一致有界性；黄依婷等[6]提出了最小二乘法观测永磁同步电机系统的参数，实现了变结构滑模控制，从而提高了系统的性能和响应速度。但是以上研究都没有分析系统的动力学行为，过于依赖所建立的数学模型。外部环境和参数的变化，系统可能会产生有害的动力学行为，比如混沌与分岔等[7]。Luo等[8]利用相图揭示永磁同步电机系统的混沌行为，提出了事件触发控制方法，以节省系统有限的通讯资源和提高系统跟踪误差精度；吴雷等[9]提出了一种微机电系统的分数阶最优控制策略，成功抑制了系统的混沌行为。系统外部扰动问题上述研究未考虑。

迄今为止，反演控制方法在面对外部干扰或参数不确定的非线性系统有着十分明显的优势。然而，传统反推控制的缺陷在于其虚拟信号求导会引起“微分项爆炸”，不仅降低系统性能，还会增加计算难度。Ma 等[10]针对不确定分数阶非线性系统设计了一种基于动态面的有效控制器。动态面控制方法虽然消除反演技术造成的重复微分产生的影响，但是会降低控制精度，导致系统性能下降；Hao 等[11]采用自适应命令滤波器控制方法，解决非线性悬架系统虚拟信号的微分项复杂的问题。

受以上研究的启发，针对带有外界扰动的永磁同步电机，本文提出加速自适应反推控制策略和2阶微分跟踪器，借助相图和Lyapunov 指数图分析系统的混沌现象，抑制系统的混沌震荡和减少系统跟踪误差的收敛时间，最后通过仿真实验证明所提控制方法的可靠性。

1 系统建模

1.1 永磁同步电机数学模型和动力学分析

基于楞次定律和基尔霍夫定律，永磁同步电机的动力学方程[12]为

为便于后续计算，对转子角速度、q-d轴的电流和时间进行无量纲变换，令因此式（1）可以重新写为

永磁同步电机具有复杂的动力学行为，当参数设置为特定的区域时，将产生混沌行为。电机的初始参数选择为γ1=5.44，γ2=20，TL=3，x1(0)=0.49，x2(0)=0.2，x3(0)=2。

图1、图2 说明电机系统存在混沌现象，会导致系统变得不稳定，影响系统性能。因此，为了抑制电机内部混沌震荡，提高其工作性能，设计有效的控制器具有重要的研究意义和现实价值。

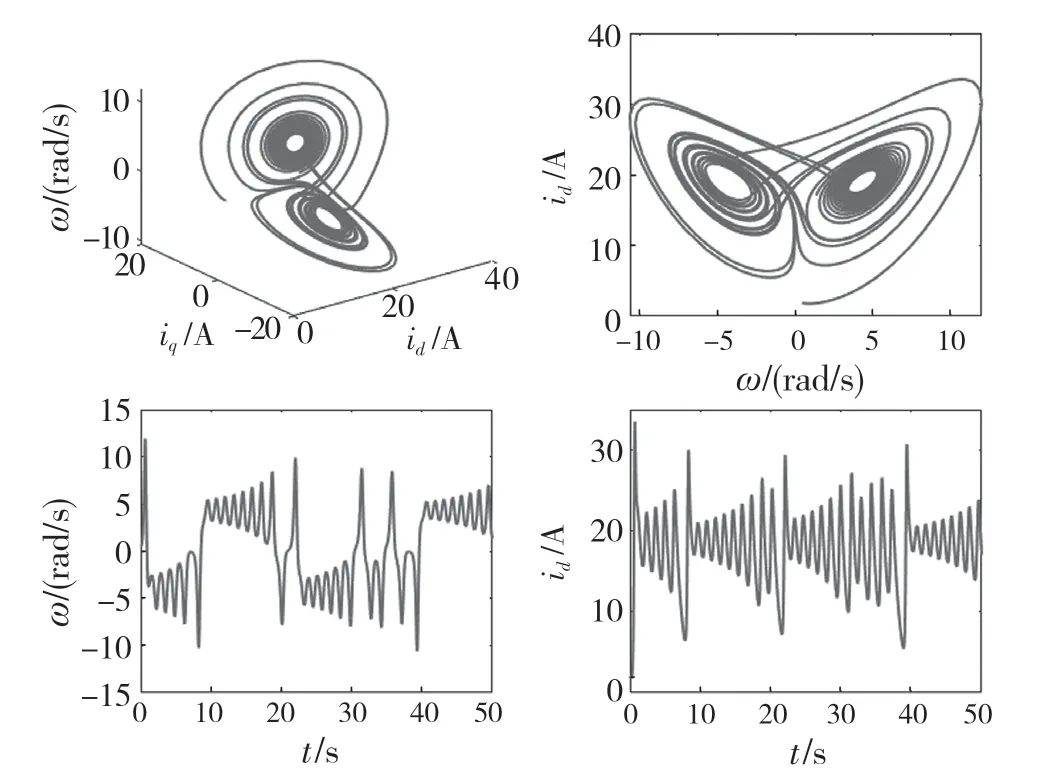
图1 永磁同步电机的相图和时间历程图Fig.1 Phase diagram and time history diagram of the PMSM

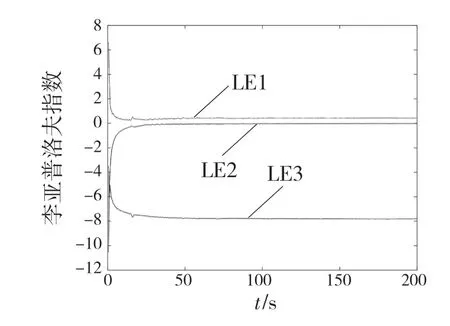
图2 李亚普洛夫指数图Fig.2 Lyapunov exponent diagram of the PMSM

1.2 区间二型模糊神经网络系统

区间二型模糊神经网络比径向基函数神经网络更擅长解决系统未知参数和外界干扰问题[13-14]，由输入层、模糊层、隶属度层、规则层、输出层构成，其工作原理可以概括为以下几个方面：

（2）区间二型模糊神经网络的IF-THEN 模糊规则定义为

式中：μil(i=1，2，…，Nn)——l阶隶属函数的i阶输入。

（3）区间二型模糊神经网络的上下激活规则为

（4）区间二型模糊神经网络的输出层的数学表达式为

区间二型模糊神经网络可以逼近任意连续函数，使如式（8）所示的不等式成立。

式中：Ωz——z的紧集；ε——逼近误差且ε>0。

2 控制器设计

为了提高永磁同步电机的瞬态和稳态过程、提高控制精度、减少收敛时间，设计的速度函数为

式中：ϑ(t)——速度函数，是严格单调递增的正定函数，初始值ϑ(0)=1；Γ——采样时间；ℓ(t)——单调非递减的任意光滑函数，令ℓ(t) 满足ℓ(0)=1 且(t)≥0；为后续控制器设计方便，令Bϑ=(t)/ ℓ(t) 。

在控制器设计中，定义跟踪误差变量zi和加速误差Si（i=1，2，3）为

自适应反演控制器的设计有以下3 个步骤。

步骤1：计算加速误差变量S1的导数

设计第1 个Lyapunov 函数：

根据式（13），对V1求导得到

根据杨氏不等式，得到

可以计算虚拟控制α和自适应控制律为

式中：χ1、Λ1、r1——控制器参数。

将式（14）—式（17）代入式（13），可得式（18）不等式

步骤2：计算加速误差变量S2的导数

设计第2 个Lyapunov 函数：

对V2求导可得

因为计算式（16）中虚拟控制α的导数很困难，容易产生“复杂微分项爆炸”问题，不利于后续的控制器设计与计算，因此设计了2 阶微分跟踪器：

式中：λ1>0，λ2>0，ϖ>0；α——虚拟控制信号输入；φ1，φ2——微分跟踪器的状态参数。

q轴控制输入uq和自适应律为

将式（24）和式（25）代入式（22），得到

步骤3：计算加速误差变量S3的导数

设计第3 个Lyapunov 函数：

对V3求导可得

d轴控制输入ud和自适应控制律为

将式（31）和式（32）代入式（30），可得

基于线性微分方程的通解，式（33）的解为

因此，PMSM 系统内的所有控制信号都是半全局一致有界的。

3 仿真实验分析

在仿真实验分析中，永磁同步电机系统的参考轨迹为xd=0.5cos（t）-0.6 sin（2t），系统的初始状态取值为x1（0）=0.49，x2（0）=0.2，x3（0）=2。永磁同步电机模型参数选择为γ1=5.44，γ2=20，TL=3。控制输入参数设置为χ1=200，χ2=150，χ3=120。自适应律参数选取为Λn=2，rn=0.5，n=1，2，3。速度函数参数取值为Γ=0.5，ℓ(t)=1。PMSM 外界干扰为d（i）=0.2x2sin（2t），i=1，2，3。2 阶微分跟踪器的相关参数定义为λ1=200，λ2=0.5，ϖ=2。最后，区间二型模糊神经网络的参数选取为隶属函数中心确定为[-0.5 0 0.5]。

图3、图4 中，实线表示有外界干扰、虚线表示无外界干扰。图3 描述了PMSM 在有无外界干扰的情况下的实际轨迹与基本重叠，实现了目标信号轨迹的高精度跟踪。在有、无外界扰动的条件下，图4 显示了d-q轴的控制输入基本重合。图5 和图6 显示了PMSM 中在系统参数变化和不同初始状态下的速度跟踪误差的对比。由此可得，提出的控制方案能有效抑制PMSM 的混沌震荡，证明所设计的控制器具有良好的抗干扰能力和鲁棒性。

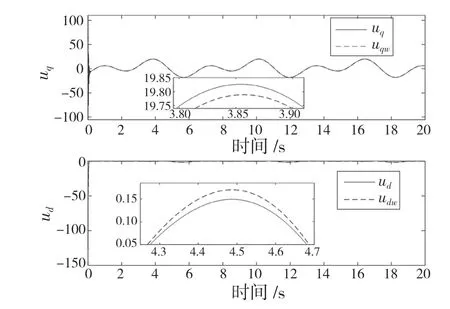
图4 有、无外界干扰的q-d 轴的控制输入Fig.4 q-d axis control input with or without external disturbance

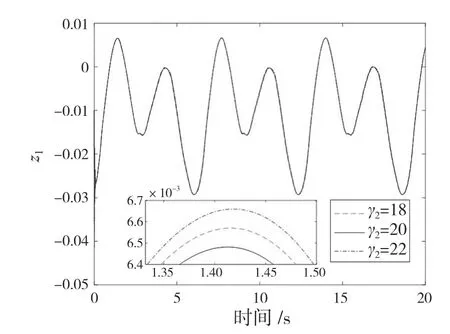
图5 当γ1=5.44 时，不同γ2下的速度跟踪误差Fig.5 Tracking errors under γ1=5.44 and different γ2

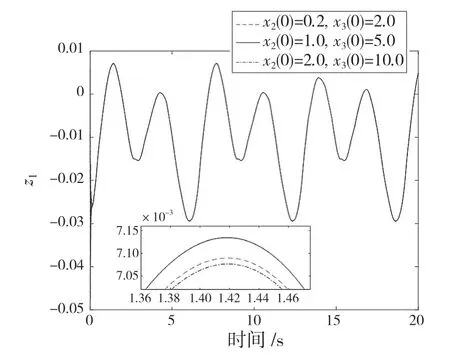
图6 不同x2(0)和x3(0)的速度跟踪误差Fig.6 Tracking errors under different x2(0) and x3(0)

4 结论

针对具有外界干扰的PMSM，本文提出了加速自适应反演控制方法。建立了PMSM 的数学建模并分析其固有的混沌现象。在控制器设计过程中，首先结合余弦障碍函数、2 阶微分跟踪器、速度函数、区间二型模糊神经网络，利用余弦障碍函数保证了状态约束不被违反；然后利用2 阶微分跟踪器处理重复微分造成的“信号爆炸”的问题，利用速度函数提高系统瞬态和稳态的工作性能，提高了控制精度；最后仿真实验证明了所设计控制器的有效性及鲁棒性。在后续研究中，将进一步解决永磁同步电机的最优控制问题。