车用高比能圆柱形锂离子电池产热行为实验表征

2023-11-27叶文盛雷齐丽娜

农业装备与车辆工程 2023年11期

叶文，盛雷，齐丽娜

(1.200336 上海市上海蔚兰动力科技有限公司；2.200093 上海市上海理工大学机械工程学院；3.475300 河南省开封市兰考县第三高级中学物理组)

0 引言

准确掌握锂离子电池的产热行为是电动汽车电池热管理的前提和基础[1]。电池的热行为包含产热特性、热场分布、温升特性，描述了电池在工作过程中热量的产生和分布状况[2]。王帅林等[3]侧重于开发电池热分析模型，通过实验分析电池的产热状况；马德正等[4]采用专用仪器分析了电池的产热行为。

锂离子电池的热分析模型大致分为2 类：宏观热分析模型和微观机理热分析模型。宏观热分析模型通常借助于数学手段，建立锂离子电池的产热率计算模型，进而通过电池工作过程中的温变状况推演其整体产热特性。典型的，Reyes-Marambio 等[5]基于分形理论（Fractal Theory）建立电池的分形时间-温度热分析模型，用以指导电池单体在风冷式热管理方案下的排布方式；Chen 等[6]基于菲克定律（Fick's Law）和傅里叶定律（Fourier's Law）建立锂离子电池的生热率理论模型，并对美国A123 公司生产的LiFePO4电池在-10～40 ℃环境温度下以0.25～3C 放电的生热特性开展实验研究；Shah 等[7-8]基于传热学导热微分方程建立了圆柱形电池的瞬态热分析模型，研究了电池热物性、换热系数等对电池热分布的影响，并建立了用以分析圆柱形电池在风冷状态下的稳态热分析模型，用以指导电池的热设计，通过实验验证了模型的准确性。除上述提到的宏观热分析模型外，亦有类宏观模型，如Botte 等[9]、Hallaj 等[10]先后提出了集中质量热分析模型，该模型将电池看作一个产热质点，通过数值模拟获取电池的整体温变状况。

微观机理热分析模型是从电池内部的基本工作原理出发，从微观层面分析电池的产热行为。美国加州大学伯克利分校的Newman 研究团队系统地提出了电池的电化学机理模型[11-12]。其中，Bernardi 等[13]在该团队研究的基础上，从电池工作过程中的微观产热层面出发，提出了包含焦耳热、可逆熵变热、混合热和相变热的电池热模型。电池的焦耳热测量通常采用阶跃电流法、电压-电流特性法和能量法，电池的可逆熵变热测量通常采用平衡电位法、可逆热等值法和焦耳热扣除法。采用这些方法测算电池的生热率耗时较长，Zhang 等[14]详述了这些方法的应用。

在采用仪器测试方面，清华大学王莉等[15]采用扩展版加速量热仪（Extend-volume Accelerating Rate Calorimeter，EV-ARC）测试了锂离子电池在不同工作温度下的产热率和放热量；Lin 等[16]采用ARC 分析了大容量40 A·h 锂离子电池（LiFePO4）的生热特性，指出电池的生热率受工作温度和工作电流的影响较大；此外，Drake 等[17]采用热流计（Heat Flux Meter，HFM）分析了18650 型锂离子电池的生热特性；Hong 等[18]采用等温量热仪分析了18650 锂离子电池的热特性，所得结果与Kobayashi 等[19]的研究结果相近。

以往关于锂离子电池热行为的研究多侧重于采用Bernardi 产热模型，测试周期长，也有部分研究采用专用设备，测试成本高。本文提出宏观电池产热测试模型——校准量热法模型，通过实验表征高比能21700 电池的产热行为，研究电池高倍率放电时的产热率、升温、工作效率等，并将其与常规热流计法进行对比，分析校准量热法的准确性。本研究有助于提升电池热测试的科学性和普适性。

1 校准量热数学模型

校准量热模型是一种考虑电池热损的精确表征模型，属于传统理想绝热模型的改良模型。它将锂离子电池工作过程中产生的总热量qcc分为2 部分：一部分热量qcc-1用于电池自加热，提升电池自身温度，另一部分热量qcc-2因热损而从电池表面流散于周围环境。

电池自加热热量qcc-1可通过能量守恒定律表示为

式中：c、m——电池的比热容和质量；Tb、t——电池温度和工作时间。

流散于周围环境的热量qcc-2可通过牛顿冷却定律表示为

式中：α、A、Ti——电池表面的对流换热系数、表面积、周围环境温度。

因此，电池工作过程中的总产热量可表示为

式中对流换热系数α可通过传热学中的非稳态测试法获取：回归分析电池温降率dTdrop/dt与温差Tb-Ti（电池Tb和环境Ti之间）的曲线关系，即：。因此，通过实验测取电池温降过程的温降率dTdrop/dt，和电池与周围环境形成的温差Tb-Ti，即可确定电池表面的对流换热系数。

2 实验方案

测试对象为高比能三元圆柱形21700 电池，外径21.44 mm，内孔径3.2 mm，高度70.25 mm；正极材料为镍钴锰酸锂（化学式Li(Ni0.8Co0.1Mn0.1)O2）；负极材料为人工石墨，其质量、比热容、容量、标称电压分别为66.7 g、1 097.8 J/(kg·℃)、4.6 A·h和3.6 V。

2.1 实验布置

图1 为NCM 21700 电池单体（破壳）的外形、热电偶布置和测试装置视图。采用锉刀和撬杠将电池破壳，破壳前放空电池电量，破壳过程中穿戴口罩、防护面罩和绝缘手套，切忌触碰和损坏电池负极集流桥接体（桥接电池外壳与负极集流体）。

图1 电池实验测试布置Fig.1 Test setup of heat generation for 21700 battery cell

将电池底壳边缘划破半个圆周，掀起约30°，将一根热电偶（T 型，丝径0.25 mm，精度± 0.4%，产自美国Omega 公司）埋入电池内孔，埋入深度为电池高度的一半（H/2），用真空封泥密封开口，并采用PI 胶带紧绷密封区域。为防止内置热电偶（TC4）脱落，在其头部蘸取适量导热硅胶，埋入后静置24 h 使其固化。图1（a）为测试装置内部，电池被夹在夹具中央，为减弱热损，采用20 mm 厚的气凝胶毡裹覆电池，将整个夹具放置于由聚苯乙烯泡沫塑料制成的尺寸为200 mm×230 mm×300 mm 的保温盒中心，用透明胶带密封装置缝隙。图1（c）中TC1～ TC4 为热电偶布置点，TC1～TC3 均匀分布于电池外径面，各热电偶间的周向角度均为120°，在轴向的相邻间距均为H/4，TC4为电池内径面热电偶布置点。

测试过程中将测试装置置于恒温箱炉内（提供初始温度和恒定的环境温度），为减弱装置与恒温箱金属托盘间的传热，在其底部铺垫3 层气泡膜。电池的充/放电过程由电池充放电仪（60 V、100 A）完成，采用安捷伦数采仪监测电池的温变状况。测试前检验了破壳操作对电池工作性能的影响，结果显示，破壳前后电池的工作电压、电容量变化分别低于1.5%和2.0%，影响可以忽略。

2.2 测试过程

（1）热损标定。将电池、测试装置及恒温箱的初始温度调至0 ℃，温度恒定后对电池以2.0C 进行充放电循环至其温度接近56 ℃时为止；然后任由电池温度下降，为节约时间，当电池温度自由下降至10 ℃时停止实验。处理数据时，为方便计算，将电池平均温度与炉温间的温差（Tavg-Ti）降至47 ℃时的时间记为0 点，并确保该温差大于下文电池放电实验中的最大温升幅度。得到电池的自由温降曲线如图2 所示。

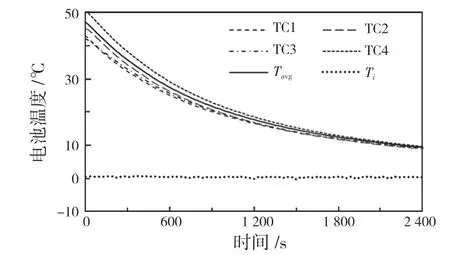
图2 电池的自由温降过程Fig.2 Free temperature drop process of battery

由图2 得到电池温降率dTdrop/dt与温差Tavg-Ti的曲线关系，如图3 所示。由图3 可将电池的温降率dTdrop/dt与温差Tavg-Ti的关系近似为线性，得到拟合方程的斜率为-9.95×10-4，cmdTdrop/dt即为电池的时变热损。

图3 电池温降率dTdrop/dt 与温差Tavg-Ti 的曲线关系Fig.3 Curve relationship between battery temperature drop rate dTdrop/dt and temperature difference Tavg-Ti

（2）测试。实验初始，电池满电（SOC为100%），调节恒温箱炉温为Ti，温度核定后给电池以X倍率放电，并实时记录电池的温变状况，直止放电结束。当Ti=0 ℃，X=1 时，电池的温变状况如图4 所示。

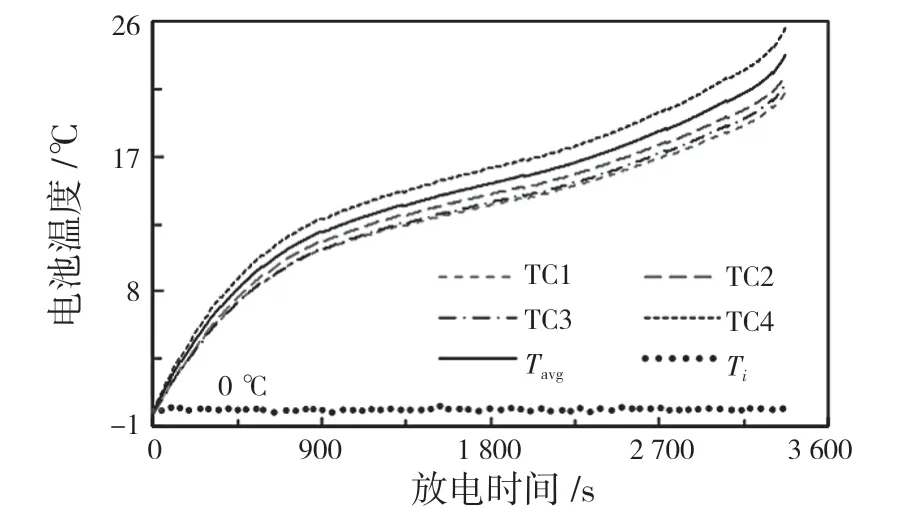
图4 电池的放电温升曲线(0 ℃，1C 放电)Fig.4 Curve of temperature rise for battery discharging (0 ℃,1C)

由图4 可见，电池工作过程中，中心温度（TC4，即Tin）较高，外部温度（TC1～ TC3）较低，这主要是由较大的电池外部热损所致。计算得到电池工作过程中主要产热部件内芯的温升率和由热损引起的温降率，如图5 所示。

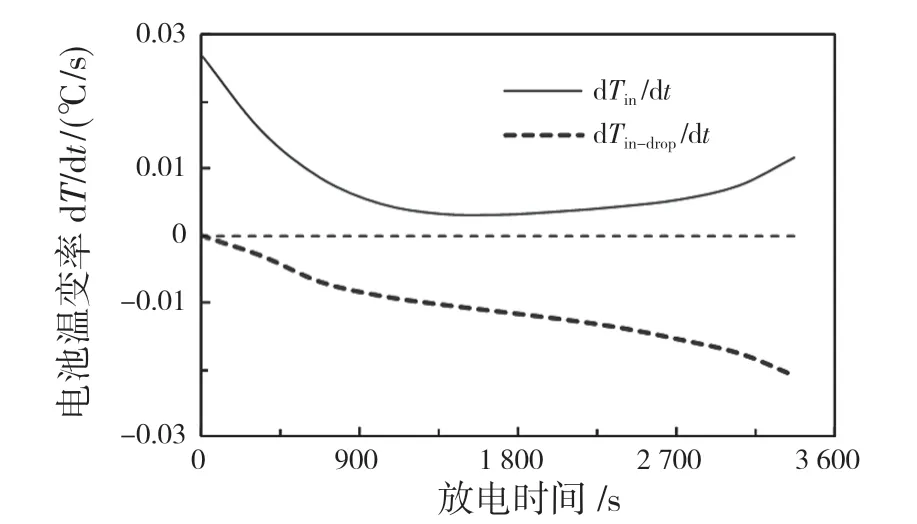
图5 电池温变率与时间的曲线关系Fig.5 Curve relationship of battery temperature variation and time

由图5 可见，电池内芯的温升率随放电时间先降后升，前期下降是由电池的温度升高使其内阻减小所致，末期又上升是由电池的内阻增大较多所致；温降率随放电时间向纵坐标轴负向逐渐增大，这主要是由电池的温升逐渐增大所致。计算得到电池表面的对流换热系数为2.5 W/(m2·℃)，进而可计算电池的产热率。

3 结果与讨论

3.1 电池的产热及升温行为

将电池放电时间10 等分，将自始至末的等分节点1、2、3、……、11 依次记为SOC值 1.0、0.9、0.8、…、0,由此得到电池在0 ℃环境下以1.0 C 放电时内芯产热率与SOC的关系如图6 所示。由图6可知，SOC在0～0.6 区间，电池内芯的产热率呈下降趋势，这主要是由电池温度上升使其内阻下降所致；SOC在0.6～1.0 区间，内芯产热率逐渐上升，在放电末期出现明显的“上翘”现象，这主要是由电池内阻增大较多所致。

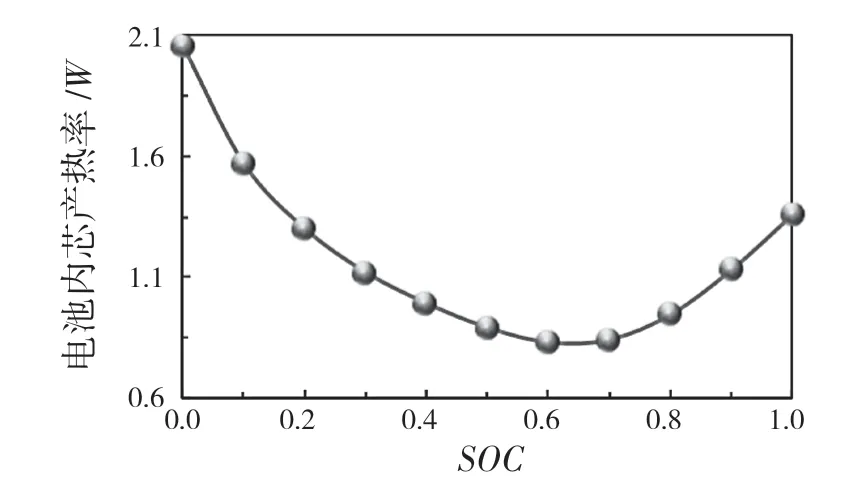
图6 电池内芯产热率与SOC 的关系(0 ℃，1C 放电)Fig.6 Curve relationship between heat generation rate of battery inner core and SOC (0 ℃,1C)

根据上述方案，得到电池在-20、-10、10、20、30 ℃环境下1C放电和在30 ℃环境下1.5C、2.0C和2.5C高倍率放电时的内芯升温幅度和放电容量，如图7 所示。由图7（a）可见，电池内芯的升温幅度随工作温度的降低而增大，放电容量随工作温度的降低而降低，当环境温度为-20 ℃时，电池放出的容量不及额定容量的85%。

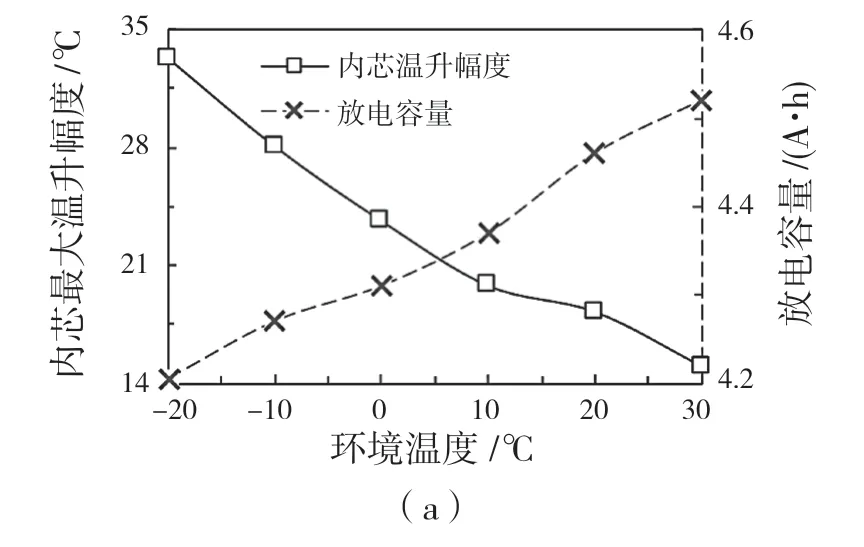
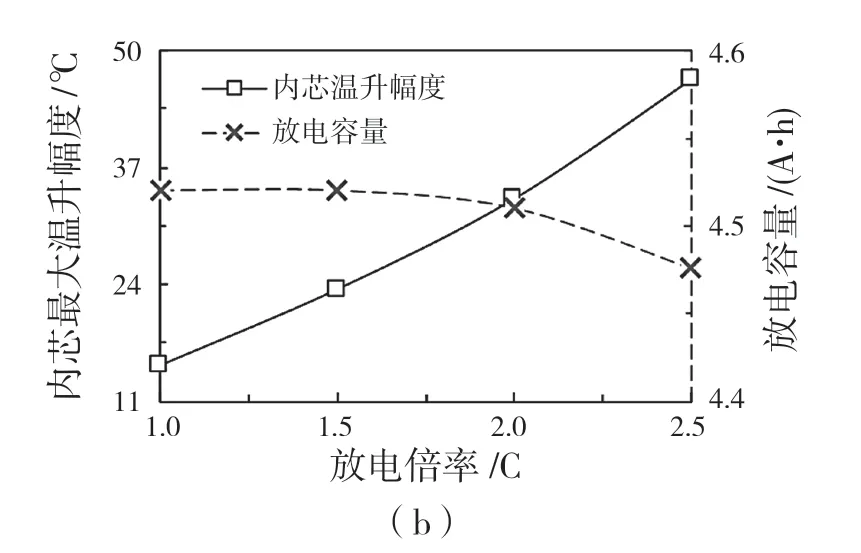
图7 电池内芯的最大升温幅度和放电容量Fig.7 Maximum temperature rise amplitude and discharge capacity of battery inner core

由图7（b）可见，电池内芯的升温幅度随工作电流的增大而增大，放电容量随工作电流的增大而降低。该现象表明，较低的工作温度和较高的工作电流对电池的工作性能具有负面影响。

依据上述分析获得电池总产热率（内芯和正/负极耳）与SOC的曲线关系，如图8 所示。由图8（a）可知，当电池以1C 工作时，其产热率随工作温度的降低而增大，主要原因为，工作温度越低电池的内阻越大，反应产生的焦耳热越多。

由图8（b）可知，当电池在30 ℃下高倍率放电时，其产热率随工作电流的增大而增大，主要原因是电池产热率与工作电流的平方近似成正比。此外，由图8（b）还发现，在每一工况下电池在放电末期其产热率均出现明显的“上翘”现象，这主要由其内阻在放电末期增大较多所致。

对电池产热率与SOC（取值0～100%）的关系进行回归分析，然后对拟合方程求积分。电池的平均产热率表达式为

计算得到电池平均产热率与工作温度、幅度倍率的关系曲线如图9 所示。由图9 可知，电池的产热率与温度、放电倍率均呈二次曲线关系，Lin 等[16]和Drake 等[17]均得到了类似趋势。

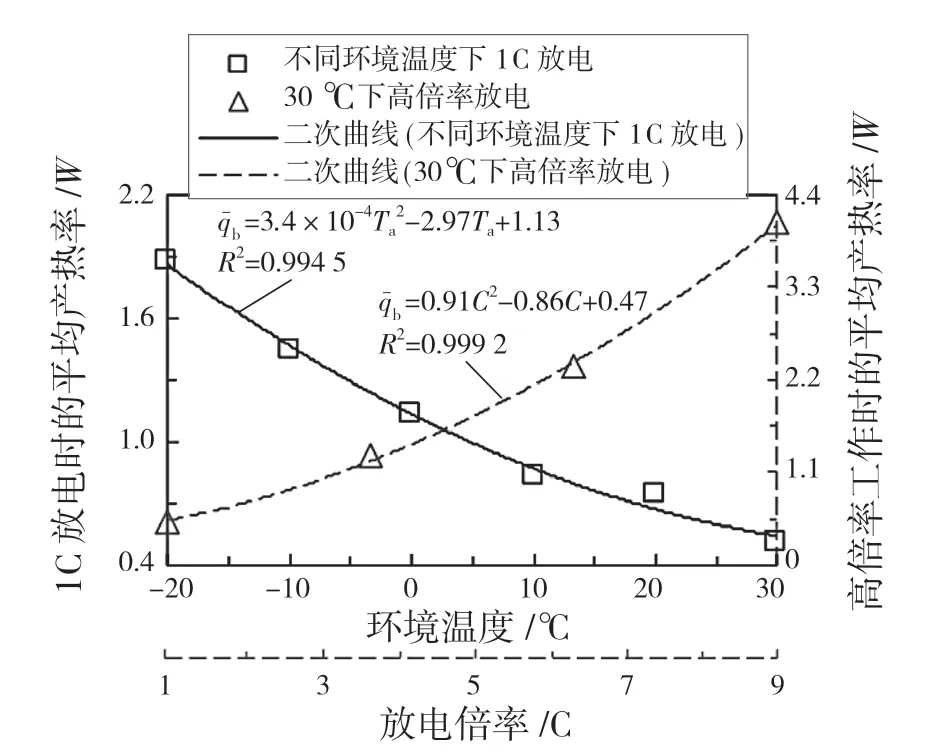
图9 电池总产热率与温度和工作电流的关系Fig.9 Relationship between total heat generation rate of battery and temperature and operating current

3.2 测试精度检验

热流计通过监测电池表面的热通量，乘以电池表面积确定电池热损，测试方程为

式中：cmdTb/dt——电池的吸热率；——电池表面的热通量。

选用日本日置电机株式会社的HIOKI-LR8432热流计，将其配套的柔性薄膜传感器（HFS，型号Z2016，精度±2%，长32.3 mm、宽10 mm、厚0.3 mm）敷于电池外侧面中部，参见图1（c）。为防止传感器弹起，采用PI 薄膜胶带将其紧绷。据此，本文利用该设备研究了上述所有工况下的电池产热率，结果如图10 所示。