不同特征水位对水电站库尾淤积分布模拟研究

田 耘，龚友龙，段钇江，杨建赞，李大成

（1.华能澜沧江水电股份有限公司，云南 昆明 650214；2.中国电建集团贵阳勘测设计研究院有限公司，贵州 贵阳 550081）

0 引言

中国河流众多，水资源丰富，水库数量庞大。水库在防洪、发电、供水、航运等方面发挥巨大作用［1］，而水库的库容是水库各种效益充分发挥最直接的保障，然而水库运行后无法避免的水库淤积问题会导致水库库容损失［2，3］，影响水库效益的发挥。尤其是库尾变动回水区的淤积摆动，泥沙淤积上延问题［4-6］，例如随着三峡坝前水位的逐步抬高，重庆主城区河段天然冲淤规律发生改变，造成碍航等问题［7］。水库特征水位不仅影响水库淤积发展过程，直接关系水库效益的充分发挥，而且是评价水库规划设计水平的重要标准［8］。因此，研究不同水库特征水位对库尾淤积分布的影响具有重要工程意义。谭志国［9］提出了不同运行方式下水库泥沙淤积三角洲随运行时间推进的特征差异性。袁晶等［10］研究认为三峡水库坝前水位是影响消落期三峡库尾河段泥沙冲淤变化的主要因素之一。叶辉辉等［11］通过库区泥沙物理模型试验研究表明不同运行方式下，汛期坝前水位对水库泥沙淤积的沿程发展、库尾淤积高程等影响较大。吴保生等［12，13］则以三门峡水库为例分析了库尾泥沙淤积受水沙条件和坝前运行方式的影响。任实［14］、李振连［15］等研究了降低坝前水位对缓解库尾河段淤积，降低排沙的作用。

本文以我国西南某电站为例，采用数学模型与物理模型相结合的方法研究模拟分析不同水库特征水位下库尾河段的淤积分布情况，从减少库尾影响的角度为水库特征水位的选择提供依据。

1 研究背景及概况

研究电站位于西藏境内色曲河汇入澜沧江的上游河段，库尾分布较多的土地和村寨，易受汛期水库回水的影响。同时，水电站库尾分布有3 号鱼类产卵场（河段长度约为2.9 km），主要产卵鱼类为澜沧江裂腹鱼、光唇裂腹鱼、裸腹叶须鱼、细尾鮡。根据水利部中科院水工程生态研究所对评价河段重要生境复核调查资料，各鱼类产卵时期主要集中在4-7月，繁殖期适宜流速范围为1.0～2.0 m/s，较适宜流速为1.5 m/s 左右。产卵场下边界距坝址66.12 km，如图1所示。因此研究水电站库尾淤积对保护库尾敏感点具有重要意义。

图1 库区河势Fig.1 River regime of the reservoir area

水库的运行调度方式分汛期和非汛期确定，其中每年6-9月为汛期，水库按汛期运行控制水位运行，其余时间为非汛期，水库按正常蓄水位运行。初步拟定推荐方案下正常蓄水位为3 054 m，汛期运行控制水位为3 040 m。为充分论证不同特征水位对库尾淤积的影响，拟定正常蓄水位为3 054 m，汛期运行控制水位分别为3 038、3 040、3 042、3 044、3 046 m；汛期运行控制水位为3 040 m，正常蓄水位分别为3 050、3 052、3 054、3 056、3 058 m等比选方案。

2 研究方法

2.1 数学模型建立与验证

2.1.1 模型建立

数学模型采用一、二维水沙数学模型相结合。其中，建立库区一维非均匀沙不平衡输沙数学模型，模型原理、计算方法及计算成果应用详见相关参考文献［16-19］。模型模拟计算范围为坝址至上游71.46 km 处，地形资料为2020年实测，包括支流共划分72个断面，断面平均间距1.08 km。

建立库尾河段平面二维水沙数学模型，模型原理、计算方法及计算成果应用详见文献［20］。模型计算范围依据库尾敏感点分布确定，下边界距离坝址66.12 km，上边界距离坝址69.00 km，模拟河段长度2.88 km。

2.1.2 模型率定

一维水沙数学模型根据坝址流量400 m3/s时实测水面线及2003年和2017年历史洪水洪痕资料，率定库区河道糙率取值范围在0.035～0.055 之间，水位验证结果见表1。考虑水库淤积后河床细化，水库淤积平衡后取为天然河道糙率的0.85～1.0倍，水库淤积过程中按淤积年限线性插值获取糙率。平面二维水沙数学模型根据定床物理模型试验成果中2003年历史洪水流量2 740 m3/s和多年平均流量621 m3/s对断面流速分布验证，验证断面取BD30-1、BD32、BD32-2、BD33-1，数学模型计算值与物理模型实测值对比如图2、3所示。模型各断面流速分布的趋势与物理模型实测值基本相同，模型精度满足计算要求。

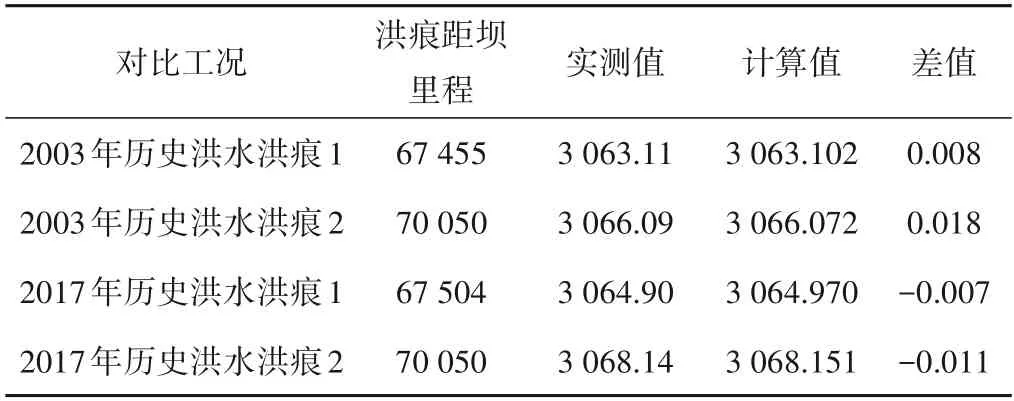
表1 水位验证结果mTab.1 Results of water level verification

图2 2003年历史洪水流量下流速分布对比图Fig.2 Contrast of velocity distributions under the flood discharge in 2003

图3 多年平均流量下流速分布对比图Fig.3 Contrast of velocity distributions under the average annual discharge

数学模型泥沙参数依据坝址上游63.10～69.26 km 河段2013年、2020年实测断面资料及2014-2019年水沙资料率定得到。率定出悬移质泥沙的恢复饱和系数冲刷时取0.25，淤积时取0.05。悬移质挟沙力的系数k取0.35，指数m取0.6。

对比上述河段2013-2020年间实际冲淤量为-21 万m3，计算冲淤量为-24 万m3，河床冲淤计算结果与实测变化结果相对误差在14.28%以内。对比河段内部分断面的形态变化，见图4，2013年-2020年间河床冲淤计算结果与2020年实测断面地形基本一致，误差较小。根据相关规范，模型参数选取正确可靠，可用于预测计算。

2.2 物理模型建立与验证

2.2.1 模型建立

根据试验研究目的和研究内容，确定模型的模拟范围上起澜沧江上游鱼类产卵场上边界以上1 km，下迄鱼类产卵场下边界以下3 km，模拟河道长度约7 km，模型平面边界见图5。

模型制作依据2020年实测产卵场河段1∶2 000河道地形图来塑造地形。采用试验河段上游水文站资料作为模型进口水沙条件，采用支流色曲水文站资料作为模型入汇水沙条件，下边界条件由数学模型提供。根据影响库尾产卵场河段淤积的主要是细沙，因此模型设计基本原则应该以悬移质运动为主，考虑推移质运动为辅，模型力求泥沙悬浮相似。根据试验河段水文资料，该河段多年平均流量621 m3/s，故模型比尺不宜过大，不然试验流量过小，影响测量，经计算确定模型水平比尺为100，垂直比尺为50，模型变率为2.0，其余各项比尺依据相关规范确定。

2.2.2 模型验证

多年平均流量下水面线验证结果见表2，模型水面线整体上与原型实测及数模计算结果接近，水位最大误差为0.07 m。同时利用2003年及2017年实测洪痕资料验证，2003年洪水流量水位最大误差为0.09 m，2017年洪水流量水位最大误差为0.12 m，符合水利部《河工模型试验规程》及《内河航道与港口水流泥沙模拟技术规程》等相关规程的误差要求。

表2 多年平均流量水面线验证成果表mTab.2 Multi-year average flow water surface line validation results

由于缺乏实测断面流速分布资料，流速分布选取多年平均流量、2003年洪水流量下各断面平面二维数学模型结果和物理模型结果进行验证，见图3。模型和原型的水面线、流速分布相似性总体较好，因此可以认为，模型满足水流运动相似条件，可以在此模型中进行不同流量级水流运动试验研究。

3 不同特征水位对水电站库尾淤积分布影响

3.1 特征水位推荐方案下水电站库尾淤积分布

3.1.1 库区深泓线变化

推荐方案下，在水库运行100年间，库区干流淤积形态为三角洲淤积，且泥沙主要在坝前59.92 km 范围内淤积；库尾变动回水区河道微冲微淤状态。随着水库运行年限的增加，三角洲顶点不断向坝前推进，起淤点则不断向水库上游延伸，库尾淤积范围增加，水库运行10年至水库运行100年后，库尾起淤点从距坝55.11 km增加至距坝59.92 km。水库运行不同年限的库区干流深泓变化见图6。

图6 库区干流河床深泓变化图Fig.6 Processes of riverbed thalweg of the reservoir area

3.1.2 河道地形变化

建库后，库区总体上以淤积为主。计算河段天然河道部分（坝址上游67.48～75.0 km段）总体上表现微冲微淤状态，断面冲淤分布上表现为深槽微冲，两岸边滩在缓流区和回流区表现为微淤；变动回水区（坝址上游66.13～67.48 km段）以微淤为主；常年回水区以三角洲形态逐渐淤积发展。因坝址断面至上游58 km范围为水库常年回水区，河道全断面基本均匀淤积。重点绘制坝上游58 km以上河段20年后地形变化等值线图，见图7。

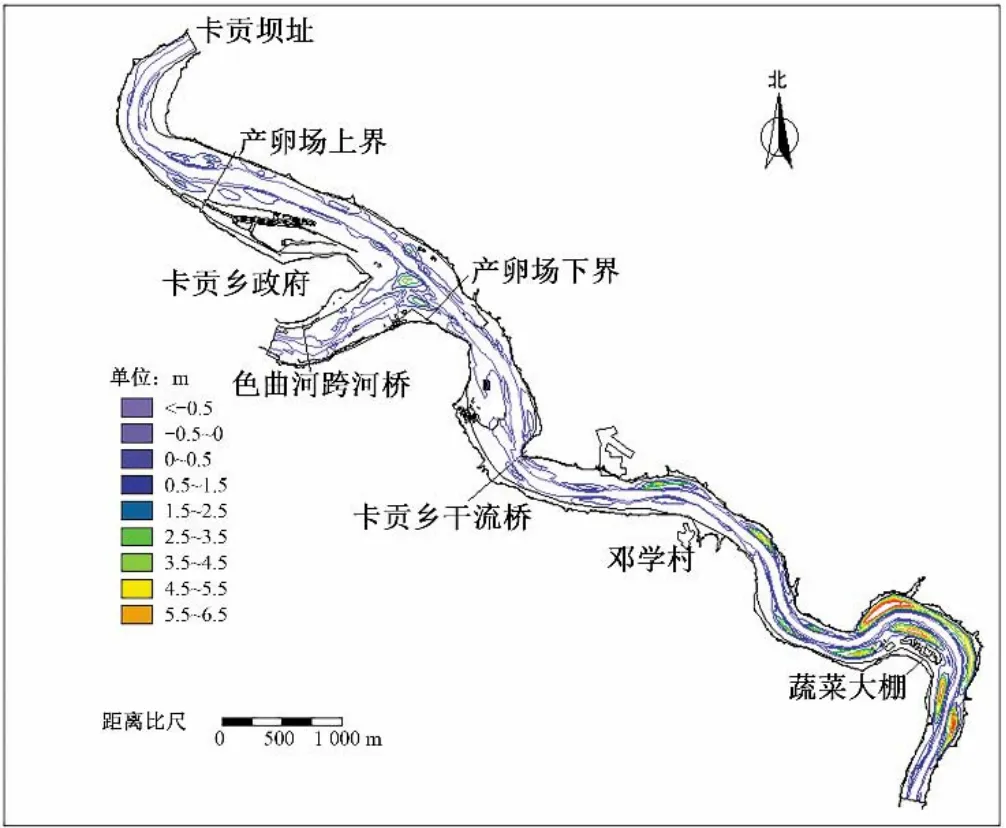
图7 地形变化等值线图Fig.7 Contour map of topographic changes

建库20年后河段深槽沿程发生微小冲刷，最大冲刷深度为1 m；两岸边滩淤积厚度在0.8～2.0 m；河道平面形态变化区淤积较大，如蔬菜大棚河段，弯道上游两岸边滩最大淤积厚度在4.0～6.5 m；色曲河入汇口门区局部淤积较大，最大淤积厚度为2.3 m。

3.1.3 冲淤量沿时程分布

水库运行100年内，库区泥沙一直呈淤积趋势，泥沙淤积量逐年增加，泥沙淤积速度逐年略有降低，库区沿程累计冲淤变化见图8。从淤积量的沿程分布来看，前10年，库区淤积主要分布在坝址上游33.33～58.16 km 河段上，此后该河段的淤积速度放缓。到20年末，淤积主要分布在坝址至上游33.33 km的河段上，水库淤积不断向坝前推进。水库运行100年内，库尾变动回水区基本不淤积，100年后距坝58.16 km 的BD27断面和距坝71.46 km的KGS断面之间河段总淤积量仅为510 万m3。

图8 库区沿程累计冲淤曲线Fig.8 Cumulative siltation curve along the reservoir area

3.2 水库特征水位不同组合下库区累计冲淤量变化

水库特征水位不同组合方案下，库区累计淤积量存在显著差异，各水库特征水位不同组合下库区冲淤总量变化见图9。坝前水位决定水库的壅水程度，进而影响库区水流挟沙力，因此库区累计淤积量随汛期运行控制水位和正常蓄水位的增加而增加，且因水库来水来沙主要在汛期，汛期运行控制水位对库区累计淤积量影响较大，正常蓄水位为3 054 m 时，6-9月运行控制水位为3 038 m 时，水库累计淤积量最小，6-9月运行控制水位为3 046 m 时，水库累计淤积量最大。不同正常蓄水位方案下的淤积量变化在3 054 m 水位处出现拐点，这是因为当水位升高到3 054 m 以上时，库尾河段断面岸坡因为存在耕地导致河宽突然展宽，过水面积突然增大导致泥沙淤积更多。

图9 水库不同特征水位组合下库区累计淤积量（单位：万m3）Fig.9 Accumulated siltation in the reservoir area under different characteristic water levels

3.3 天然情况及建库后水库特征水位不同组合方案下产卵场区淤积分布

因汛期运行控制水位对库区淤积影响较大，因此对比天然情况冲淤变化50年和建库后各汛期运行控制水位不同方案下50年后产卵场区域典型断面冲淤分布，如图10。天然情况下产卵场区河段地形变化表现为微冲微淤状态，断面分布上表现为冲槽淤滩。由于建库后推荐方案运行下各流量级回水尖灭点均未达到产卵场下边界，该方案运行时产卵场区域河段冲淤分布和天然情况下基本相同。对比分析除推荐方案外其他方案产卵场区河段地形变化可见，正常蓄水位为3 054 m 时，6-9月运行控制水位3 038 m 方案对产卵场区域河段冲淤分布和天然情况下相同，对冲淤分布无影响。6-9月运行控制水位3 042 m方案因回水影响，产卵场区域河段滩面淤积略有增大，深槽冲刷影响不大。

图10 各运行方案下50年后产卵场区域典型断面冲淤分布Fig.10 Changes in typical cross-sections of spawning ground areas after 50 years

以产卵场上边界断面BD34 为例，因正常蓄水位为3 054 m时，6-9月运行控制水位3 038、3 040、3 042 m 方案汛期回水未影响到该断面，断面冲淤分布基本同天然情况，主槽冲刷在0.5～1.0 m 左右，两岸滩地淤积厚度在0～1.8 m；正常蓄水位为3 054 m时，6-9月运行控制水位3 044、3 046 m方案汛期回水对该断面略有影响，滩面淤积厚度在0～2.0、0～2.2 m。再以产卵场下边界断面BD32为例，因正常蓄水位为3 054 m 时，6-9月运行控制水位3 038、3 040 m方案汛期回水未影响到该断面，断面冲淤分布基本同天然情况，主槽冲刷在0.4～1.2 m 左右，深泓右移约20 m，色曲河汇流区下游滩地淤积厚度在0～1.0 m；正常蓄水位为3 054 m 时，6-9月运行控制水位3 042、3 044、3 046 m 方案汛期回水对该断面冲淤略有影响，影响程度随6-9月运行控制水位的增高而增加，如6-9月运行控制水位为3 046 m 时，主槽冲刷在0.6 m 左右，深泓右移约25 m，左岸形成新的边滩，淤积厚度约1.5，色曲河汇流区下游滩地淤积厚度在0～2 m。

3.4 数学模型结果和物理模型结果对比

为验证数学模型结果的合理性，将建库1年后、20年后河床平面冲淤分布与典型断面淤积分布物理模型实测成果与数学模型计算成果进行对比分析，见图11、图12。综合几个典型断面冲淤形态的对比，建库20年后河床冲淤分布总体呈现微冲微淤状态，断面分布上表现为冲槽淤滩，总体冲淤分布特征物理模型实测成果与数学模型计算成果基本相同。

图11 物理模型试验与数学模型的断面冲淤分布对比图Fig.11 Comparison of physical model and mathematical model of cross-sectional siltation distribution

图12 物理模型试验与数学模型的平面冲淤分布对比图Fig.12 Comparison of physical model and mathematical model for planar siltation distribution

以建库20年后为例，河槽冲刷深度在0.5 m 左右。滩地淤积幅度数学模型计算成果与物理模型试验成果总体上基本相同，局部淤积区数值模拟结果偏大，主要差别在汇流区，建库20年后，物理模型的滩地淤积厚度在0.6～1.2 m，汇流处淤积最厚在1.2 m，数学模型的两岸滩地淤积厚度在0.4～2.0 m，汇流处最大淤积厚度达2.3 m。分析原因可能是，物理模型试验中能充分反映汇流区局部水流的紊动挟沙能力，平面二维水沙数学模型将水流流速及含沙量沿垂线平均，在紊动变化较强的汇流区忽略了近底床面泥沙的紊动促发，导致局部淤积偏大。从另一角度，也说明数模计算结果偏安全。

4 结论

本文以澜沧江流域某电站为例，采用数学模型和物理模型相结合的手段研究不同水库特征水位组合方案对库尾淤积的影响，主要结论如下。

（1）建库后，库区总体上以淤积为主。计算河段天然河道总体上表现微冲微淤状态，断面冲淤分布上表现为深槽微冲，两岸边滩在缓流区和回流区表现为微淤；变动回水区以微淤为主；常年回水区以三角洲形态逐渐淤积发展。因坝址断面至上游58 km范围为水库常年回水区，河道全断面基本均匀淤积。

（2）库区淤积量随汛期控制水位和正常蓄水位的升高而增加，且汛期控制水位的影响程度相对较大。

（3）数学模型与物理模型结果相互印证，不同水库特征水位组合方案下，库尾淤积分布较天然情况表现为滩面淤积略有增加。