管道输水灌溉系统运行状况数值模拟及应用

2023-11-27郑天翼蔡守华

中国农村水利水电 2023年11期

郑天翼，蔡守华，张璇

（扬州大学水利科学与工程学院，江苏扬州 225009）

0 引言

管道输水灌溉是一项以管道代替明渠进行输水的灌溉工程技术［1］。利用管道进行输水可以有效减少输水损失，节省土地，同时也有益于灌溉的自动化控制与管理［2］。目前，管道输水灌溉技术在我国北方地区已得到广泛应用，在南方小型机电灌区的推广应用也得到了高度重视［3，4］。相比于北方井灌区，南方地区管道输水灌溉系统的控制面积较大，轮灌组同时工作的放水口数也比较多，因此利用数值模拟手段，模拟不同工作条件下各放水口流量及系统相关技术参数，对于提高其技术水平具有重要意义。数值模拟是分析评估输水管网技术性能的重要手段，广泛应用于管网工程设计与管理研究［5］。早期灌溉管网的数值模拟研究主要集中在微灌与喷灌系统，这类研究［6，7］通常利用水力学基本公式建立相应的数学模拟模型，而后采用迭代试算的方法进行求解，最终获得各级管道的流量与工作压力等参数，常见的迭代方法有牛顿法［8］、梯度法［9，10］等。为了适应不同地形条件的需要，王昊利等［11］开发了考虑地势起伏变化的微灌系统水力仿真软件，可用于模拟复杂地貌条件下微灌系统的水泵工况点以及各级管道的工作压力等参数。蔡守华［12］根据水力平衡原理建立喷灌系统的数学模拟模型，该模型可以模拟稳定运行条件下各级管道、喷头以及水泵的各项技术参数。近年来随着南方管灌工程的建设发展，有关管道输水灌溉系统数值模拟的研究引起了重视。为改善管道输水灌溉系统的灌水均匀性，蒋晓红等［13］通过改进常规设计方法建立管灌系统水力模拟模型，该模型可用于模拟各放水口的流量与工作压力。为评估管道输水灌溉系统设计方案的合理性，龚志浩等［14］提出了基于水量平衡与能量守恒原理的水力模拟模型，并采用粒子群算法进行求解，应用该模型可以获得稳定状态条件下水泵的工况点以及各级管道和放水口的实际流量。上述研究可以模拟灌溉管网部分技术参数，但目前尚未见可全面模拟管道输水灌溉系统管网及水泵机组各主要技术参数的数值模拟研究。因此，本文以小型机电灌区管道输水灌溉系统为对象，建立管道输水灌溉系统运行状况数学模拟模型，旨在为改进管道输水灌溉系统用水管理提供技术手段，同时也为管道灌溉系统设计方案优选与智能控制奠定技术基础。

1 基本原理

在南方平原河网地区，机电灌区管道输水灌溉一般以河水为灌溉水源，可控制的灌溉面积较大，作物以稻麦为主。管网通常由干、支两级管道组成，系统扬程较小，水泵多采用混流泵。管道输水灌溉系统开始工作后，经过一段短暂的水力过渡后即可达到稳定运行状态［12］。此时整个灌溉系统具有以下特点：

（1）当前轮灌组所控制的各级管道的工作压力和流量、各放水口的工作压力和流量、以及水泵的各项性能参数均达到稳定，且保持不变［15］。

（2）管网系统中各接头、弯头、以及三通等节点的上下游断面之间均遵循恒定流质量守恒定律、能量守恒及转化定律［16］。

（3）系统中水泵的工况点必定为水泵性能曲线（Q～H）与系统需要扬程曲线（Q～H需）的交点，即水泵所提供的扬程与管网系统所需要的扬程相等［17］。

水泵的稳定运行工况点需要经过多次试算求得，下面分析基本求解思路。在确定系统处于稳定运行工况后，首先为当前工作的最远一个放水口假定一个工作压力，然后由远及近地对管网各节点建立水力平衡方程（即连续性方程与能量方程），从而得到系统各主要节点的流量与工作压力，最后通过计算得到管网系统所需扬程，并与水泵可提供的扬程相比较，根据比较结果按一定的规则调整最远放水口的工作压力，经多次调整、推算与比较，直至水泵所提供的扬程与系统所需要的扬程相等，即可得到系统稳定运行状态下水泵的工况点。与此同时，各放水口及各节点的工作压力与流量也一并达到稳定运行状态。

2 构建模型

下面以图1所示的管道输水灌溉系统为例建立数学模型。根据南方机电地区管道输水灌溉工程的轮灌特点，假设实行双支轮灌，轮灌方向如图中的箭头所示，当前轮灌组中工作的支管分别为第i支与第j支，两支管上分别开启ni与nj个放水口。

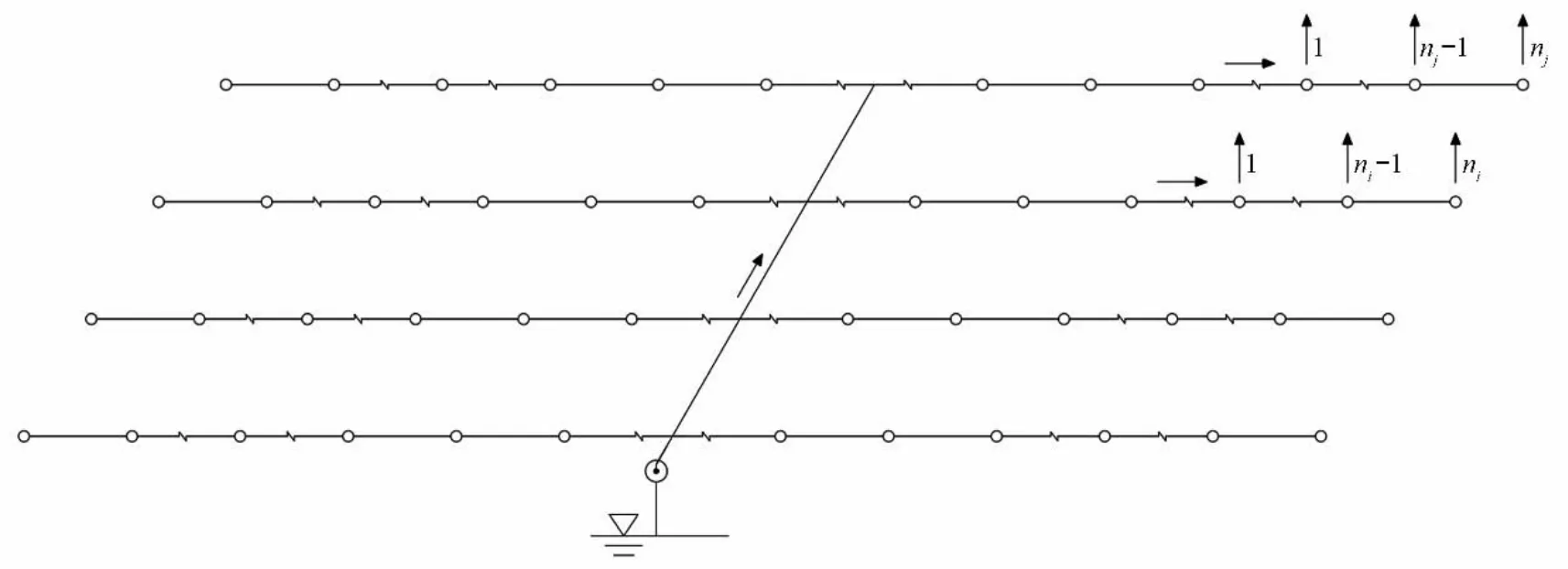
图1 管道输水灌溉系统的一般布置形式Fig.1 General layout of the irrigation networks with pipe conveyance

2.1 支管水力计算模型

这一部分组成包括当前轮灌组在该支管上所开启的末端放水口、非末端放水口、以及各放水口分流节点上游的支管节间管段。下面以第j支为例建立这一部分的数学模型。

（1）末端节点水力计算。

式中：Qc(j，nj)为j支上的末端放水口的流量，m3/s；μ为放水口的流量系数；A为放水口的过水断面面积，m2；g为重力加速度，取9.81 m/s2；Hc(j，nj)为j支上末端放水口的工作压力，m；Qz(j，nj)为j支上的末端放水口节点上游支管节间管段的流量，m3/s；Hs(j，nj)为j支上的末端放水口节点上游断面的工作压力，m；Vs(j，nj)为j支上的末端放水口的进口平均流速，m/s；f为管道摩阻系数；m为流量指数；Ls为竖管长度，m；Ds为竖管内径，m；ζ1为变径直角弯头局部阻力系数；b为管径指数。

（2）中间节点水力计算。

式中：Lc(j，k+1)为j支上开启的第k+1 个放水口的上游支管节间管段的长度，m；Dz为支管内径，m；Zc(j，k+1)为j支上的第k+1 个放水口的上游支管节间管段的两端高差，m；ζ2为直流三通局部阻力系数；ζ3为折流三通局部阻力系数。

（3）支首流量及工作压力。根据式（4）～（7），由远及近，依次对j支上开启的各个非末端工作放水口部分进行计算，在得到j支上第1个非末端工作放水口的上游支管节间管段的流量、工作压力后，利用下式计算j支支首的流量、工作压力：

式中：Qz(j)为j支支首流量，m3/s；Hz(j)为j支支首工作压力，m；ζ4为支首闸阀局部阻力系数。

2.2 干管水力计算模型

这一部分组成为当前轮灌组控制的干管管段，下面建立这一部分的数学模型：

式中：Qu(i)为i支节点上游支管节间管段的流量，m3/s；Hu(i)为i支节点上游断面工作压力，m；Lg(j)为j支节点上游支管节间管段的长度，m；Dg为干管的内径，m；ζ5为i支与j支之间的干管上各支流四通局部阻力系数之和；Vg(i)为i支节点上游支管节间管段内的平均流速，m/s；Zg(j)为j支节点上游支管节间管段的两端高差，m；Hu′(i)同样为i支节点上游断面工作压力，加“′”以示区分，m；Qg为干首流量，m3/s；Hg为干首工作压力，m；ζ6为干首到i支节点的各局部阻力系数之和。

2.3 水泵水力计算模型

这一部分组成包括水泵以及水泵进水管段，下面建立这一部分的数学模型：

式中：Qb为水泵流量，m3/s；Lj为进水管的长度，m；Dj为进水管的内径，m；ζ7为进水管进口到水泵出口各局部阻力系数之和；Vj为进水管内的平均流速，m；Zj为进水管两端高差，m；Zx为水泵出口到水源水位的高差，m；Hb为系统需要水泵扬程，m；Hb′为水泵实际扬程，m；η为水泵效率，%；P为水泵轴功率，kW。

以上式（17）～（19）分别为水泵扬程性能曲线函数、效率性能曲线函数以及轴功率性能曲线函数。

3 求解模型

根据管网系统各部分的计算特点，采用计算简便的二分法进行迭代计算。下面仍以图1 为例，以第i支和第j支同时工作为典型轮灌组，说明模型的具体求解步骤。

步骤1：对轮灌组在j支上开启的末端放水口的工作压力Hc(j，nj)按经验取一个足够大的可能取值区间(h1，h2)，并令Hc(j，nj)=(h1+h2)/2，由式（1）～（3）分别求得Qc(j，nj)、Qz(j，nj)、Hs(j，nj)。

步骤2：对轮灌组在j支上开启的各个非末端放水口的工作压力取一个足够大的可能取值区间(h5，h6)，自末而首依次对各放水口进行计算。以j支上第k个非末端放水口为例，令Hc(j，k)=(h5+h6)/2，由式（4）～（5）分别求得Qc(j，k)、Qz(j，k)，将结果代入式（6）～（7）分别求得j支上第k个非末端放水口的上游支管节间管段工作压力来自不同分流方向的计算结果Hs(j，k)与H′s(j，k)，若|Hs(j，k)-H′s(j，k)|＜E，则结束迭代并进入下一步计算；否则作以下判断：Hs(j，k) ＜H′s(j，k)则令h6=(h5+h6)/2；Hs(j，k) ≥H′s(j，k)则令h5=(h5+h6)/2，重复步骤2计算，直至满足本步骤的精度要求。然后依次对支管上其余非末端放水口进行类似计算，直到计算到该支第1个放水口为止。

步骤3：对轮灌组在i支上开启的放水口的工作压力取可能取值区间(h3，h4)并进行与j支相同的计算。

步骤4：由式（8）～（9）分别求得i支与j支支首流量与工作压力，由式（10）～（12）求得i支支管分流结点上游断面工作压力的来自不同分流方向的计算结果Hu(i)与Hu′(i)。若|Hu(i)-Hu′(i)|＜E，则结束迭代并进入下一步计算；否则作以下判断：Hu(i) ＜Hu′(i) 则令h4=(h3+h4)/2；Hu(i) ≥Hu′(i) 则令h3=(h3+h4)/2，返回步骤3 重复计算，直至满足本步骤的精度要求。

步骤5：根据式（13）～（16）计算得到水泵流量Qb与系统需要扬程Hb，根据式（17）得到水泵实际扬程Hb′。若|Hb-Hb′|＜E，则结束迭代并进入下一步计算；否则作以下判断：Hb＜Hb′则令h1=(h1+h2)/2；Hb≥Hb′则令h2=(h1+h2)/2，返回步骤1。重复以上各步骤计算，直至满足精度要求。

步骤6：根据式（18）～（19），求得水泵效率与轴功率。

4 实例分析

某地拟建如图2所示的管道输水灌溉系统。灌溉面积约15.8 hm2，地面平坦，地面高程8.50 m，土壤为砂壤土。以附近河流为灌溉水源，设计低水位为3.50 m。作物为稻麦轮作，以水稻泡田定额为设计灌水定额。水稻格田长110 m，宽30 m，每个格田布置1 个放水口。系统设计灌水周期取4 d，分8 个轮灌组，每天工作2组。每组包括2条支管，其中每条支管开启3个放水口，灌水时间10 h。干管、支管管材均采用PVC-U 塑料管，管径分别为DN355、DN250，水泵选用200HW-8型混流泵。

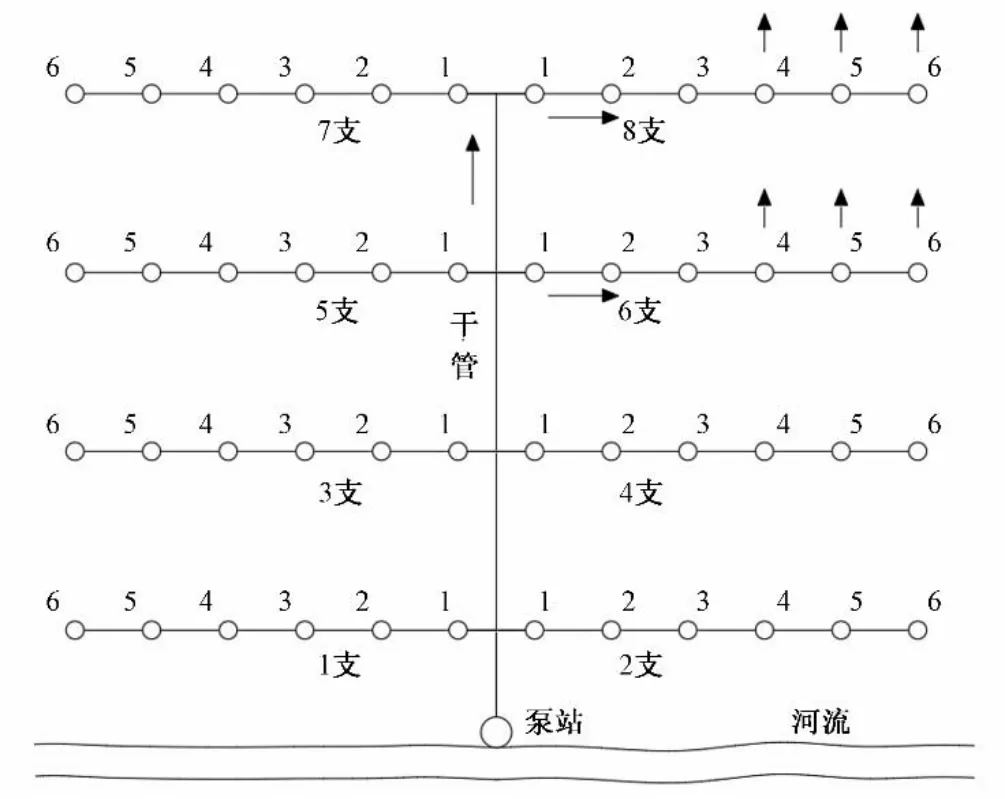
图2 管道输水灌溉系统布置图Fig.2 Layout of the irrigation networks with pipe conveyance

利用本文所构建的模拟模型对上述设计方案进行模拟，模拟结果如表1所示。各轮灌组的水泵效率最低为80.20%，最高为82.05%；水泵轴功率最小为9.39 kW，最大为9.40 kW；水泵实际扬程最小为7.67 m，最大为8.50 m；放水口流量最小为55.72 m3/h，最大为66.72 m3/h。从模拟结果来看，各轮灌组对应的水泵稳定运行工况点均能落在高效区范围内；但各放水口流量差异较大，若各放水口采用同样的放水时间10 h，会导致各田块灌水量出现较大差异。为减少各放水口灌水量偏差，若放水口有条件调节流量，用水户可通过调节放水口流量，减少各放水口灌水量偏差；或者在转换轮灌组时，开阀先开流量较小的放水口，关阀先关流量较大的放水口。

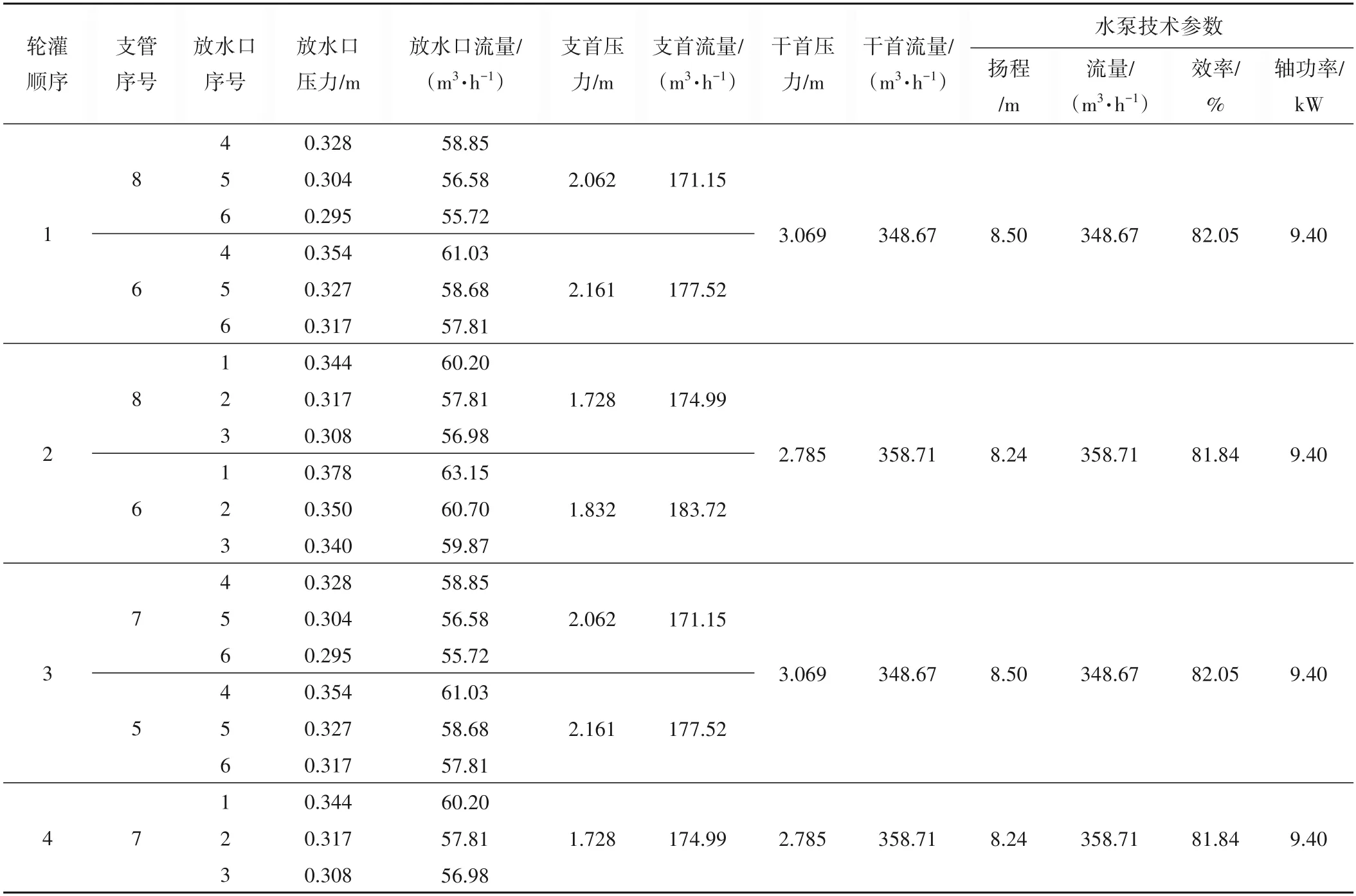
表1 管道输水灌溉系统模拟结果Tab.1 Simulation results of the pipeline irrigation system

系统实际运行时，可能出现水源水位变化较大的情况。利用本模型可以模拟系统各项技术参数可能随之发生的变化，以水源水位5.50 m 为例，模拟结果显示：各轮灌组的水泵效率最低为70.50%，最高为73.80%；水泵轴功率最小为8.80 kW，最大为9.02 kW；水泵实际扬程最小为6.14 m，最大为7.20 m；放水口流量最小为62.79 m3/h，最大为74.30 m3/h。用水户可依据模拟结果的变化情况，适当调节放水口的放水时间，改善灌水的均匀性。

日常用水管理时，也可能出现用水户随意改变轮灌方案的情况。利用本模型可以模拟系统相关技术参数的变化情况，从而判断是否采用该轮灌方案。如将轮灌组同时工作的支管数调整为1 条，每条支管上同时工作的放水口数调整为6 个，每天分2 组进行轮灌。该方案模拟结果显示：放水口流量最小为73.16 m3/h，最大为82.16 m3/h，且水泵效率最低为58.20%，较设计轮灌方案的水泵效率明显降低，因此不宜采用该轮灌方案。