基于有限元法的水轮发电机组临界转速研究

姬联涛，袁浩强，荆岫岩，王 璞，刘 昊，杨雍杰，李超顺

（1.中国电力科学研究院有限公司，江苏 南京 210003；2.华中科技大学 土木与水利工程学院，湖北 武汉 430074；3.国家电网有限公司，北京 100031；4.国网湖南省电力有限公司，湖南 长沙 410004）

0 引言

水电作为一种可再生能源，由于其诸多天然优势，在我国使用极为广泛，各流域大中小型水电站建设数量众多。随着国内更多中高水头水电站的建设与增容改造，机组运行工况更加恶劣、稳定运行要求更高，在实际运行过程中，当机组转速上升到一定值时，激振力频率与轴系固有频率相近，且作用方向与振型方向一致时，轴系会产生强烈振动，该转速被称为临界转速［1］。若机组在此转速下长时间运行，可能造成结构损坏、噪声加剧，严重危及厂房及工作人员的生命财产安全，因而对水电机组轴系振动特性尤其是临界转速的研究愈发重要。

目前针对此类转子系统振动特性分析，国内外学者已经做了大量的研究：荣吉利等［2］基于有限元法自主编制程序ROTOR，对红石和隔河岩水电站轴系的自振特性进行计算与分析，并与试验结果进行对比；HUA 等［3］利用Muszynska 非线性密封力，构建转子与密封的动力模型，并通过分岔图和庞加莱图分析了密封如何干扰系统的稳定性；杨晓明等［4］采用有限元法建立水电机组轴系横向振动力学模型，并在考虑轴承简单耦合关系下求解了固有频率与临界转速；LUNENO 等［5］针对组合轴承对水电机组转子不同方向的耦合作用，分析其改变机组固有频率与振动模式的机理；翟黎明等［6］利用SAMCEF ROTOR 程序建立了抽水蓄能发电机组转子-轴承-电磁系统三维有限元模型并分析了不平衡磁拉力与导轴承刚度变化对临界转速的影响；马晨原等［7］采用有限元分析软件探究了发电机质量偏心及导轴承刚度变化对机组振动特性的影响，并与现场测量数据进行对比；徐瑞红等［8］利用ANSYS 软件对某水电站轴系进行模态分析与临界转速计算，得出其发生共振可能性很小的结论。

以上研究为水电机组轴系的动态特性分析与结构优化提供了借鉴，但多数模型过于简化，各类轴承与密封装置的耦合作用未充分考虑，不能够真实地反映出机组的边界条件与工作状态。鉴于此，本文针对某水电站的混流式机组，考虑上导、水导和推力轴承的耦合关系，分别构建无机械故障、转子或转轮质量偏心、联轴法兰不对中的有限元分析模型，进行转子动力学仿真求解临界转速，从而分析轴系的动态性能。

1 转子动力学仿真原理

转子动力学分析主要包括稳定性分析、临界转速计算和不平衡响应三部分［9］，起初科研工作者们多数采用传递矩阵法，但随着计算机运算性能的提高，研究者们更加青睐于精度更高、直观性更强的有限元法。基于有限元动力学仿真推导出来的完整转子动力学微分方程为：

求解转子系统临界转速，就是在给定转子系统转速Ω的前提下，求解系统涡动转速ω。当所得涡动转速ω与给定转速Ω相等时，便称此转速为临界转速，该涡动转速下的振型就是临界转速的振型。

2 物理模型

2.1 几何参数

由水轮机与发电机图册可知该机组为二导悬式混流式水轮发电机组，即存在两个导轴承与一个推力轴承，利用三维可视化建模软件UG，采用传统的自底向上建模方法，即先对机组的转轮、水轮机主轴、发电机大轴、转子机架、磁极、磁轭、推力头等部件进行精细化建模随后装配，最终得到轴系计算简图与三维装配模型如图1所示。

图1 轴系计算简图与三维装配模型Fig.1 Shafting calculation diagram and three-dimensional assembly model

2.2 材料参数

根据图纸结合各部分的物理特性，轴系各部件材料参数统计如表1所示，在ANSYS中建立材料库，并根据表1对机组各部分进行材料赋值。

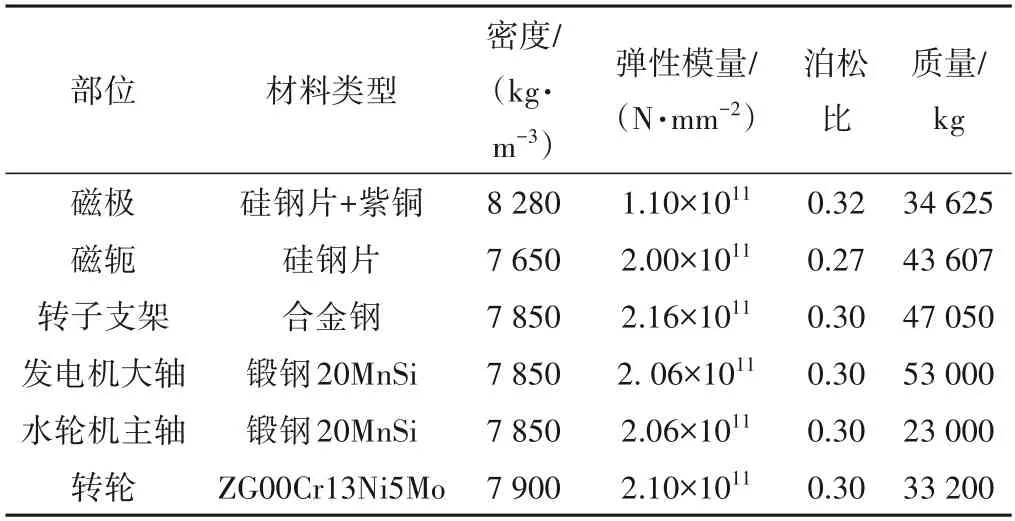
表1 轴系各部件材料参数统计Tab.1 Material parameter statistics of shafting components

3 有限元模型

3.1 网格划分

为了节约计算资源，并保证仿真结果的精度，采用映射划分、自由划分与扫掠划分相结合的方法，并在网格不连续处设置绑定接触，单元类型为六面体20 节点的SOLID186 与四面体10 节点的SOLID187 单元，经划分的模型节点数为359 150，单元数为164 660，结果如图2所示。

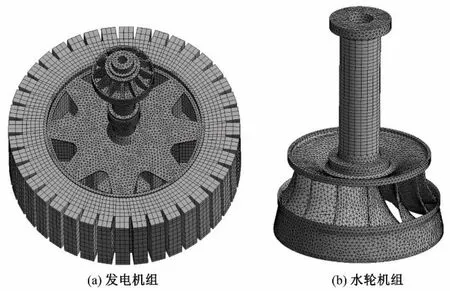
图2 水轮发电机组网格划分结果图Fig.2 Grid division result of hydro-generator set

3.2 边界条件

该二导悬式水轮发电机组的固有频率很大程度上受到水导、上导、推力轴承等边界条件的影响，故在保证高精度物理模型的基础上合理简化边界条件尤为重要。对于实际的水电机组，轴承座、轴瓦和机墩等都具有一定弹性，在使用弹簧阻尼器模拟各轴承时，其弹簧刚度可视为油膜刚度、轴承座与机墩刚度三者的串联，由于本研究着重分析轴系的振动特性，故假设轴承座与机墩为刚性，仅考虑油膜动力特性参数。

3.2.1 导轴承

为了准确模拟上导和水导轴承的油膜刚度与阻尼，本文采用Lund 提出的八参数模型［10］，其对应ANSYS 的弹簧阻尼单元COMBI214，包括线性化的4 个刚度系数与4 个阻尼系数，COMBI214单元几何结构如图3所示。

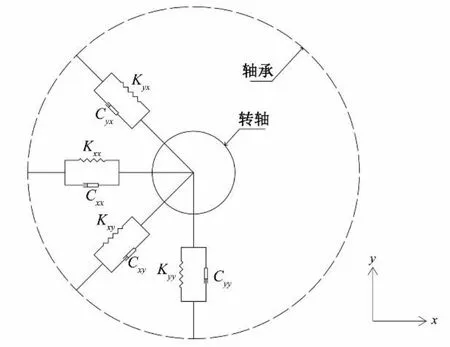
图3 COMBI214单元几何结构Fig.3 The geometry of COMBI214 unit

将支承视为各向同性，忽略交叉刚度与阻尼的影响，其主刚度与主阻尼可通过油膜力求得，但是油膜力表达式无法直接由流体润滑的Reynolds 方程导出，故选择无限短轴承理论［11］对轴承做近似处理，得到导轴承无量纲刚度系数和阻尼系数的解析表达式为：

式中：K为无量纲刚度系数；C为无量纲阻尼系数；B为导轴承长度；D为导轴承直径；ε为轴颈中心的偏心率，等于偏心距离与轴承半径间隙的比值。

导轴承刚度系数与阻尼系数的有量纲表达式为：

式中：k为有量纲刚度系数；c为有量纲阻尼系数；μ为润滑油度；n为轴颈转速；L为轴承轴向长度；φ为轴承间隙比，等于轴承半径间隙与轴颈半径的比值。

将涉及到的相关参数代入以上公式，轴颈中心偏心率取0.4，求得额定转速下各导轴承刚度系数与阻尼系数：上导轴承刚度系数为8.55×106N/mm，阻尼系数为1.39×105（N·s）/mm；水导轴承刚度系数为7.09×107N/mm，阻尼系数为1.37×106（N·s）/mm。

3.2.2 推力轴承

考虑到推力轴承对轴系不仅有轴向的支撑作用，当镜板随轴的弯曲振动而倾斜时，油膜力还会提供恢复力矩，相当于一个扭转弹簧。因而将推力轴承约束视为伸缩弹簧与扭转弹簧的共同作用，其油膜刚度系数与阻尼系数可通过文献［12，13］所提供的解析表达式并结合自身参数求得，轴向刚度系数取为8.50×108N/mm，阻尼为1.01×106（N·s）/mm；扭转刚度系数取为3.18×109（N·s）/rad，阻尼为7.64×107（N·s）/mm。

最终得到轴系三维有限元模型如图4所示。

图4 轴系三维有限元模型Fig.4 Three dimensional finite element model of shafting

4 计算结果与分析

4.1 无机械故障的轴系振动特性分析

所谓无机械故障是指理想状态下水电机组各部件的加工与设计阶段完全一致，不存在材料的缺损、发电机转子与水轮机转轮的偏心与变形、联轴法兰不对中、轴系整体不对中等故障，且设备的安装精度达到100%。利用轴系有限元模型考虑陀螺效应在八个转速点下进行复模态分析，采用QR Damped 法提取各阶模态，水电机组轴系前八阶振型如图5所示。

由图5 可知，前两阶振型表现为以两个导轴承为支点的摆动，转轮下环处位移最大、推力头次之；第三阶为转轮的扭转变形，下环处位移最大且沿周向均匀分布；第四、五阶振型的危险点位于推力头上端，其次是转轮，其余部位几乎不发生振动；第六、七阶主要表现为推力头、转子、转轮的振摆，其中位移最大处仍位于推力头上端与转轮下沿；第八阶振型下水轮机很安全，主要表现为发电机整体的摆动，推力头处位移最大。随后利用复模态分析结果绘制该转速范围内固有频率与转速相关激振频率的关系曲线，即Campbell图，结果如图6所示。由于本研究主要针对轴系的径向振动特性，故排除扭转振型对应的模态分析结果，前四阶固有频率随机组转速的变化情况如表2所示。

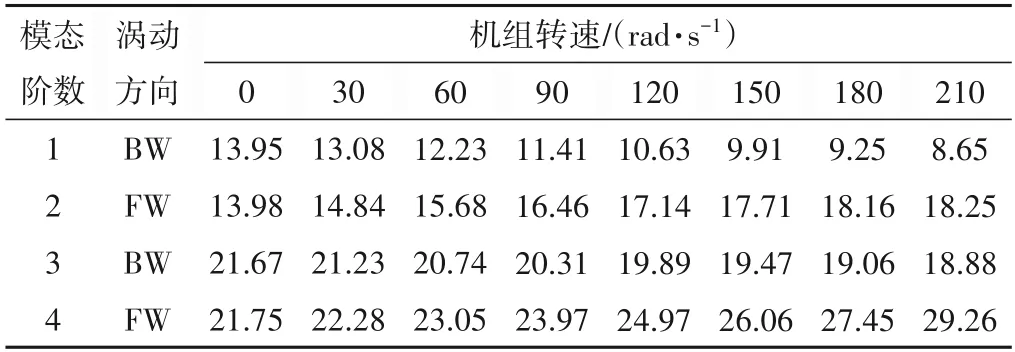
表2 前四阶固有频率随机组转速的变化情况Tab.2 Variation of the first four order natural frequencies with unit speed

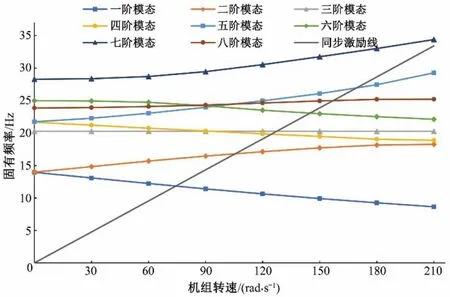
图6 无机械故障下轴系Campbell图Fig.6 Campbell diagram of shafting without mechanical failure

结合图6 与表2 分析可知，随着机组转速增大，正向涡动固有频率上升，反向涡动固有频率下降，前四阶临界转速分别为：74.35、105.64、124.55、169.38 rad/s，但第一、三阶为反向涡动，在实际运行过程中该共振并不会被激发，因而其并不能称作真正意义上的临界转速。对于水轮发电机组，一般要求第一阶临界转速为飞逸转速的1.4 倍以上［14］，由资料可知该机组的飞逸转速为300 r/min，即31.42 rad/s，远小于正向涡动的第一阶临界转速，故满足设计要求，机组在正常运行时不会发生共振现象。

4.2 质量偏心对轴系振动特性的影响

由于水电机组在安装阶段的误差或者长期运行过程中的磨损变形，在轴系的主要部位，即发电机转子和转轮往往会出现质量偏心问题，为探究其偏心率其对轴系振动的影响，首先计算出理想工况下两者的质量、体积、质心位置、转动惯量等物理参数，再以该发电机定转子间的平均气隙长度，即27 mm 为基准，由平行轴定理［15］计算出转子与转轮分别偏心20%、40%、60%后的参数变化，结果如表3所示。

表3 转子与转轮物理参数随偏心率的变化情况Tab.3 Variation of rotor and runner physical parameters with eccentricity

在ANSYS 中采用mass21 单元分别模拟发电机转子或水轮机转轮偏心对轴系的影响，随后以同样方式绘制Campbell 图并计算各阶临界转速，得到临界转速随转子或转轮偏心率的变化情况如表4所示。

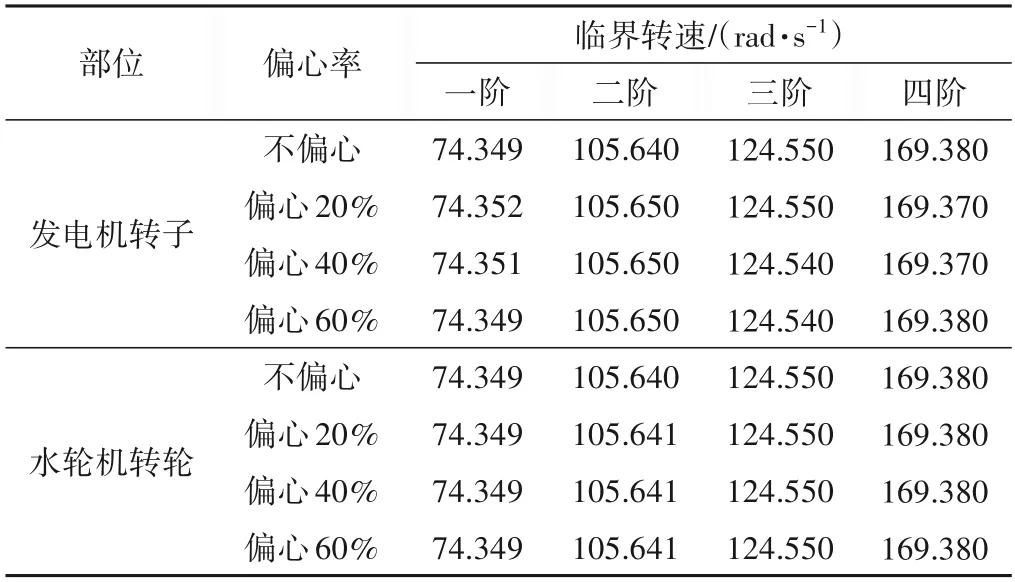
表4 临界转速随转子或转轮偏心率的变化情况Tab.4 The variation of critical speed with the eccentricity of the rotor or runner

由表4 可知，随着发电机转子或者水轮机转轮偏心率的增大，前四阶临界转速的变化微乎其微，变化幅度不超过0.01%，因而可以得出结论：至少在该偏心范围内，转子与转轮的质量偏心不会对轴系临界转速产生影响，即临界转速与单纯的质量偏心无关。

4.3 联轴法兰不对中对轴系振动特性的影响

由电站资料可知，水轮机轴与发电机轴通过法兰结构连接，联轴螺栓为20 条铰制孔销钉螺栓，其规格为M115×6 mm，长度为480 mm，在机组吊装过程中不可避免地会造成一定的误差，因而联轴法兰不对中现象普遍存在，为了探究偏心距离对临界转速的影响，本文分别建立了联轴法兰偏心10、50、100 mm的有限元模型并进行转子动力学分析，得到临界转速随联轴法兰偏心距离的变化情况如表5所示。

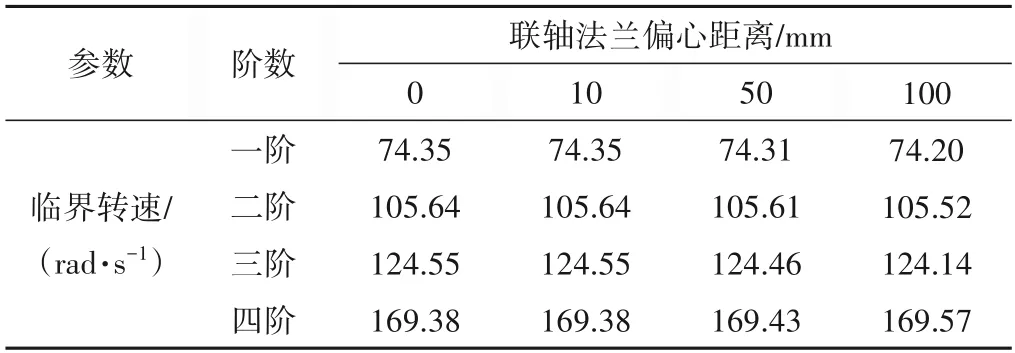
表5 临界转速随联轴法兰偏心距离的变化情况Tab.5 Variation of critical speed with eccentric distance of coupling flange

由表5可知，随着联轴法兰偏心距离的增大，低阶临界转速呈减小态势，高阶临界转速略微增大，当联轴法兰偏心距离为100 mm时，前三阶临界转速减小，第四阶临界转速增大，与对中情况相比，增减幅度最大不超过0.33%，且实际运行过程中联轴法兰偏心距离远达不到该数值，因而可以得出结论：水电机组临界转速受到联轴法兰不对中的影响不大。

5 结论

基于限元法建立了水轮发电机组轴系高精度动力学模型，考虑了上导、水导和推力轴承的耦合关系并计算出各向刚度与阻尼值，在无机械故障、转子或转轮质量偏心、联轴法兰不对中3种工况下进行了转子动力学仿真，得到各阶模态固有频率、振型以及临界转速。通过分析可知：该水电机组轴系在上述3 种工况下的临界转速均满足要求，且受质量偏心与联轴法兰不对中的影响很小，该研究对水轮发电机组结构优化设计具有一定的意义。