基于改进自适应遗传算法的新安江模型参数率定研究
2023-11-27赵杏杏叶瑞禄丛小飞刘修恒
左 翔,赵杏杏,叶瑞禄,丛小飞,刘修恒
(1.南京河海智慧水利研究院,江苏 南京 210012;2.南京中禹智慧水利研究院有限公司,江苏 南京 210012;3.河海大学计算机与信息学院,江苏 南京 211100)
0 引言
精准可靠的水文预报对于提高防洪“四预”能力具有重要意义[1,2]。由于水文过程具有不确定性和高度非线性的特点,在水文模拟时需要通过模型参数率定来校准水文模型,使其模拟效果与实际水文过程相匹配。采用合适的优化方法率定复杂的水文模型参数,一直是国内外不断探索的热点课题。随着人工智能技术的发展,大量优秀的人工智能算法被应用模型参数的率定,如遗传算法[3-5]、粒子群算法[6]、洗牌复形演化算法(Shuffled Complex Evolution,SCE-UA)[7,8]等。基于人工智能算法的模型参数自动优化方法,能够比人工优化方法更易、更快地找到全局最优解,避免人为的主观偏见和误差,对提高水文预报精度具有重要意义。
遗传算法(Genetic Algorithm,GA)[9]是一种模拟生物遗传进化过程的全局优化概率搜索算法,因其简单通用、鲁棒性好和全局搜索能力强等特点,已成为水文模型参数率定的一个重要研究方向。针对传统遗传算法局部搜索能力弱,过程控制参数依赖人工经验,存在不成熟的过早收敛或者收敛缓慢等难题,研究人员采用多种方法提高遗传算法性能。王森等人[10-12]根据SRINIVAS[13]提出自适应遗传算法(Adaptive Genetic Algorithm,AGA),采用线性自适应交叉与变异概率公式,对种群的进化过程进行控制,避免种群早熟及过早收敛;杨从锐等人[14,15]采用反正弦函数的非线性自适应交叉与变异概率公式,能够根据种群个体的适应度值全程优化交叉与变异概率。目前遗传算法经过自适应优化后,仍然存在着初始种群多样性差,局部搜索自适应能力弱,以及自适应调整缺乏对种群进化程度的考虑等问题。针对上述问题,通过采用混沌算法优化初始种群,结合自适应交叉与变异概率算子,以及环形交叉算子和自适应非线性变异算子,对传统遗传算法过程进行一系列优化改进,提出了一种新型的改进自适应遗传算法(Improved Adaptive Genetic Algorithm,IAGA)。将IAGA 算法应用于秦淮河流域的新安江次洪模型参数率定,从水文过程模拟、率定收敛性和稳定性等方面与GA 和AGA 算法进行对比研究,综合评估IAGA算法在新安江模型参数率定工作中的应用性能。
1 新安江模型参数
新安江模型属于概念性水文模型[16],适用于湿润半湿润地区水文模拟,主要包含4 个计算模块,分别为:蒸散发、产流、水源划分和汇流,其中蒸散发采用3层蒸散发模式,产流采用蓄满产流模型,水源划分为地表径流、壤中流与地下径流,汇流模块中壤中流与地下径流采用线性水库法,河网汇流采用采用滞后演算法,河道演进采用分段连续演算的马斯京根法[17]。新安江模型的主要参数、参数意义及取值范围如表1所示。

表1 参数取值范围Tab.1 Value ranges of parameters
2 遗传算法
GA 算法是根据自然界中生物“适者生存、优胜劣汰”的进化过程推演出来的一种寻优方法[18],标准计算流程由Goldberg首先提出[19],首先制定实际问题中变量的编码方式,设定种群规模、交叉概率、变异概率、迭代次数等参数,再通过随机函数生成初始化种群,利用适应度函数对种群中个体进行评价,淘汰适应度低的个体后,种群中的个体进行交换和变异形成新种群,再对新种群进行淘汰选择交换变异,通过不断循环,最终在种群中产生适应度最高的个体。
3 改进自适应遗传算法
GA 算法在实际应用中存在易陷入局部最优、收敛不成熟、收敛速度慢等问题,难以求解得到全局最优解[5]。本文通过引入混沌算法和自适应算子,改进初始种群生成、选择、交叉与变异等过程,以期提高遗传算法性能。
3.1 编码方式
种群个体的染色体编码方式通常采用二进制和十进制两种方式[20],算法采用十进制编码,与二进制编码相比,十进制浮点数编码具有直观、节省时空开销、计算效率高的优势。将新安江模型的1个参数设为1个染色体基因片段,参与优化的w个参数构成1个种群个体。
3.2 适应度函数
GA 算法在搜索过程中以适应度函数值来评估个体的优劣程度。本文以确定性系数(Coefficient of Determination,R2)和纳什效率系数(Nash-Sutcliffe Efficiency Coefficient,NSE)组成坐标,计算方法分别如式(1)和式(2)所示,以坐标对到点(1,1)的欧式距离[式(3)]作为次洪径流模拟过程与实测过程之间的拟合程度指标[21]。由于目标函数F(x)是求其最小值,在转换为适应度函数f(x)时需要采用如式(4)所示的方法,适应度值越大,被遗传到下一代的概率也就越大,则代表的目标函数值越小。
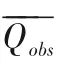
3.3 初始种群
初始种群的多样性和质量直接决定着最终解的质量和算法的收敛速度。GA 算法采用随机函数生成的初始种群多样性较差,因此限制了GA 算法的求解性能。本文采用一种结合混沌搜索生成初始种群的改进方法,提高初始种群多样性,并且能够从混沌搜索结果中选取适应度较高的个体作为初始种群,进一步提高初始种群的质量,从而加快算法的收敛速度[22,23]。混沌搜索采用的Logistic映射公式如式(5)所示:


3.4 选择策略
选择采用轮盘赌选择法(Roulette Wheel Selection method)[24],染色体的适应性越高,被选择的机会就越大。同时为保护当前群体中最优个体的染色体信息,采用精英保留策略,适应度最高的个体不进行交叉和变异操作,直接复制到下一代,保护种群最优个体的染色体信息免遭破坏。
3.5 自适应交叉变异概率
交叉概率Pc和变异概率Pm是影响遗传算法收敛速度与搜索能力的重要参数,传统GA算法采用固定的Pc和Pm值,当Pc和Pm取较大的值时会提高种群多样性,但容易破坏个体的优良染色体基因;当Pc和Pm取较小的值时会减少种群多样性,种群容易陷入局部最优导致过早收敛。针对上述问题,SRINIVAS[13]提出了自适应遗传算法(AGA),其公式如下所示:
式中:fʹ为待交叉的两个个体中较大的适应度值;fmax为种群的最大适应度:favg表示种群的平均适应度;f表示变异个体的适应度;k1~k4为自适应控制参数,文献[13]取k1=k3=1.0,k2=k4=0.5。当个体适应度低于当代种群平均适应度时,采用较高的交叉和变异概率,以提升个体进化速度;当个体接近当代种群最大适应度时,采用较低的交叉和变异概率,尽可能保留该个体的优良染色体基因。但是该种算法缺乏对整体种群进化程度的考虑,在进化初期适应度值高的个体不一定是全局最优解,采用较小的交叉变异概率,会导致算法早熟或走向局部收敛;另一方面AGA算法,对于小于平均适应值的个体采用固定的交叉变异概率,无法实现对种群全部个体的自适应调控。
综上所述,对于遗传算法过程的自适应调整应当充分考虑种群的进化程度和个体的适应度两大因素[25],针对种群的进化程度,本文设计了反应种群进化程度的适应度函数离散系数γ,在进化初期种群的适应度函数离散性系数γ0最大,随着种群的进化,个体逐步向最优解逼近,离散性越来越小,理论上γ 将趋近于0。
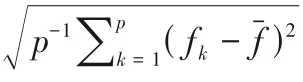
随着遗传算法进化代数t的增加,种群适应度平均水平不断提高,重复个体也逐渐增多,使得群体中个体适应度离散程度逐渐减低。依据自适应调整需要,结合适应度函数离散系数定义,改进后的自适应遗传算法交叉概率和变异概率公式如下:

由公式可以看出,IAGA 算法主要从种群进化程度和个体适应度两个维度进行交叉变异概率的自适应调整。对于整体种群,在进化初期应采用较大的Pc和Pm,在值域空间范围内进行全局搜索,提高进化效率,在进化后期种群逐渐逼近全局最优解,应采用较小的Pc和Pm,使其稳定收敛于最优解;对于种群个体,适应度值高的个体,采用相对较小的Pc和Pm,保留优良基因,适应度值小的个体,采用相对较大的Pc和Pm,提高进化效率。通过改进的自适应交叉变异概率,综合保障遗传算法在前期有高效的全局搜索能力,在后期有较好的稳定性和收敛性。
3.6 环形交叉
传统单点交叉和双点交叉算子在个体基因互换时,染色体中基因被选中的概率不相等,位于中间的基因被选中的概率较大,而两端基因被选中的概率较小,从而影响整个解空间的搜索范围。本文采用环形交叉算子[28],该算子可以环绕整个染色体两端来进行交叉,每个基因被选中的概率相等,有利于提高算法的全局搜索能力。
3.7 自适应非均匀变异
遗传算法属于全局性寻优算法,局部搜索寻优能力较弱,变异算子主要用于提高遗传算法的局部搜索能力,防止出现早熟收敛,因此变异是比较重要的算法环节。针对十进制浮点数编码方式,传统采用均匀变异算子,即用一定范围内均匀随机数代替原有的基因,但是不能根据种群的进化程度灵活的调整搜索区域。针对上述问题,研究设计了自适应非均匀变异算子,在进化初期在大区域范围内搜索,加强个体变异;在进化后期,在局部区域搜索,促进个体向最优解收敛。将个体xi(i=1,2,…,w),通过自适应非均匀变异算子得到x’i(i=1,2,…,w),其公式如下:
3.8 总体步骤
IAGA算法的基本流程和步骤如下:
(1)参数初始化。主要包括:种群规模p,混沌变量个数m,最大进化代数T,带求解问题维度w,交叉与变异的相关参数等。
(2)种群的初始化。将m个混沌变量映射到优化变量x的取值空间,并选取适应度值较高的p个个体组成初始种群。
(3)评价适应度值。采用适应度函数评价种群个体的适应度,并保留适应度最大的个体,不参与选择、交叉与变异过程。
(4)选择选择采用轮盘赌选择法,从父代中选择出优良个体,生成下一代个体。
(5)交叉运算。对种群无放回地抽取一对个体,根据自适应交叉概率Pc和环形交叉算子来进行这一对染色体的基因片段交换,重复p/2次完成种群的交叉操作。
在这个过程中,教师首先要让学生明白,英语口语交际中出现错误是在所难免的,这些都是其口语交际能力提升的重要过程。说错并不可怕,怕的是不敢去用英语进行来表达。当出现错误的时候,我们就能够知道自身在口语上的问题,发现问题进行改正,才能够更好的将英语说出口。
(6)根据自适应变异概率Pm和自适应非均匀变异算子对个体的染色体进行变异操作,对染色体基因的值进行局部搜索形成新的变异值。
(7)停止进化条件判断。一般通过判断当前进化代数t是否达到最大进化代数T来决定进化是否结束;未达到停止条件返回步骤(3),对新种群进行适应度评价,完成种群适应度的更新,并对比新一代最优个体的适应度是否大于当前最优个体,如果大于就用新一代最优个体进行替换;达到停止条件,进入下一步骤。
(8)最终结果输出。将进化过程中最优个体染色体所代表的最优解进行输出。
4 实例验证
秦淮河是南京的“母亲河”,发源于溧水河、句容河,总体流向自东南往西北。流域呈蒲扇形,长宽各约50 km,四周为丘陵山区,占80%;中间腹部为低洼圩区和河湖水面,占20%。地势从南向北倾斜,上游坡度和扇面大,中下游坡度缓,共有大小16条支河汇入,是一个典型的一干多支树状型河道,如图1所示。大都为山丘河道,具有源短、坡陡、流急、汇流快的特点,出口处又受江潮顶托,造成排水不畅,历史上洪涝灾害不断。

图1 秦淮河水系图Fig.1 Stream network of Qinhuai river basin
如图1所示前垾村(秦)水文站位于句容河与溧水河交汇处,该站点以上为秦淮河上游,受到人工调度及潮汐顶托的影响相对较小,以下垫面、分水线、站点布设等为主要依据划分水文计算单元,采用分布式新安江模型对秦淮河上游的汛期径流过程进行模拟。研究所用的前垾村(秦)水文站2009-2017年的汛期逐时径流量数据从《中华人民共和国水文年鉴——长江流域水文资料》中的实测流量成果表获取,其中前7 场用于率定,后3 场用于验证,分别利用GA、AGA 和IAGA 三种算法对新安江模型参数进行优化,分析三种优化算法在新安江模型参数优化问题中的应用差异。
4.1 验证设计
新安江模型总共有16 个参数,若都参与率定,通常导致参数组的最优解不稳定且不唯一,参数的率定结果不一定符合实际意义。具体操作过程中,假定各参数取值在流域各子计算单元保持一致,根据流域下垫面资料并结合已有经验来固定部分参数[29],包括WUM、WLM、WDM、C、WM、B、IM、L,其值如表2所示,并固定结构性约束KG+KI=0.7,主要对K、SM、EX、KI、CS、CI、CG参数进行率定。通过降低整个待优化参数组的维数,既结合模型自身的水文特性,同时也充分发挥了遗传算法优越性,提高了优选运行效率。

表2 参数WUM、WLM、WDM、WM、B、IM、C、L的人工率定结果Tab.2 Manual optimization results of WUM,WLM,WDM,WM,B,IM,C,L
为验证IAGA 算法在新安江模型参数率定中的应用性能与效果,以传统GA 和AGA 算法为参照,分别从率定收敛性、率定耗时、率定稳定性和洪水模拟效果4 个方面进行度量与分析,3种算法的参数设置见表3。

表3 GA、AGA 和IAGA算法参数设置Tab.3 Parameter settings of GA,AGA and IAGA
4.2 结果与分析
4.2.1 率定收敛性
率定收敛性研究分别采用GA、AGA 和IAGA 算法对所选敏感参数进行优化迭代率定,求出目标函数的最优值,分析3种优化算法的收敛速度和收敛结果,图2 曲线图反映了3 种优化算法的收敛过程。
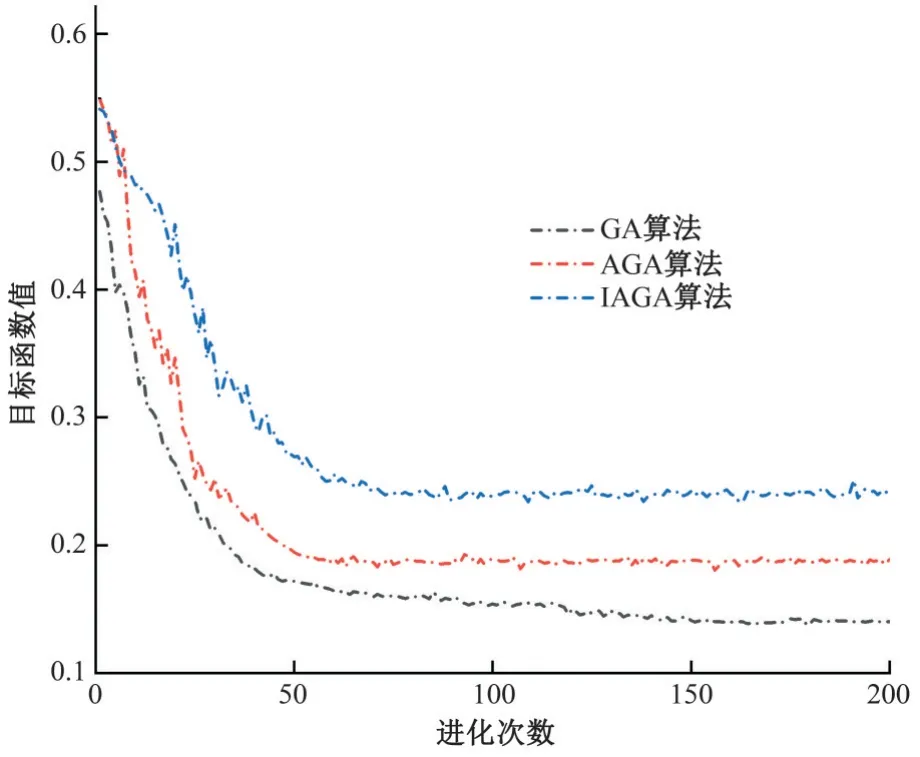
图2 GA,AGA和IAGA算法的收敛过程Fig.2 Convergence procedure of GA,AGA and IAGA
在种群进化的初始阶段,IAGA 算法由于引入了混沌搜索算法遍历性的特点生成初始种群,在经过优选后,其初始最大适应度优于随机生成初始种群的GA 和AGA 算法,不仅增加了种群多样性,而且提高了初始种群质量。
在种群进化的过程中,AGA 和IAGA 算法通过参数自适应调整,提高了初期种群优良染色体基因的遗传概率,其收敛速度比GA算法明显更快,且具有更强的全局搜索能力;但是AGA算法的自适应Pc和Pm算子,在进化后期会过度保留优良染色体基因,在初期虽然能够比IAGA 算法更快的进化,但是随着种群离散性的减小,无法自适应的降低优良基因的保留概率,导致过早的局部收敛,未能解决GA 算法早熟的问题。因此从收敛结果来看,虽然GA和AGA算法能够在较少的迭代次数下收敛,但是并没有寻求到最佳的个体。由于IAGA 算法采用了自适应调整的算子,能够根据种群进化程度和个体适应度调整Pc和Pm。初期采用较高的Pc和Pm,提高种群多样性,避免早熟,后期采用较小的Pc和Pm,避免优良基因的破坏,保障稳定收敛;结合环形交叉算子和自适应非均匀变异算子,综合调整交叉变异效果,IAGA 呈阶梯状,摆脱了局部收敛,体现出了较强的自适应能力,IAGA算法在寻优能力上明显优于GA和AGA算法。
在种群进化的收敛阶段,GA和AGA算法波动高于IAGA算法,一方面由于GA 和AGA 算法采用固定或部分固定的Pc和Pm值,在进化后期种群仍然保持较大的交叉与变异概率,容易破坏种群优良的染色体基因,不利于后期稳定的收敛;另一方面IAGA 采用了自适应非均匀变异算子,随着进化的收敛种群离散性的降低,通过自适应的缩小变异的搜索范围,保证算法收敛的稳定性。
4.2.2 率定耗时
率定耗时研究从小到大选取多个迭代次数,GA、AGA 和IAGA 算法的率定耗时如表4所示,GA 算法的参数率定耗时最少,其次是AGA 算法和IAGA 算法。GA 算法简单,进化耗时少,但是收敛所需的迭代次数高于AGA 算法,而且率定效果最差;AGA 算法复杂度小于IAGA,能够以最小的进化代数收敛到最优值,率定效果优于GA 算法,劣于IAGA 算法,在对一些精度要求不高的问题进行优化时可以利用该优势,从而缩减优化时间,提高计算效率;IAGA 算法由于采用多种复杂的自适应算子,需要确定的算法参数多,计算过程较为复杂,导致其计算量大,优化模型参数的时间较长。总体来说,遗传算法中耗时较长的主要是适应度函数计算步骤,因此采用自适应交叉与变异算子后,对率定耗时影响不大。

表4 GA、AGA和IAGA算法在不同进化代数下的率定耗时sTab.4 Time-consuming of GA,AGA,IAGA under the different number of generations
4.2.3 率定稳定性
率定稳定性取决于算法能否在各次相同的迭代次数下,得到稳定分布的参数值,因此可以从各参数方差和目标函数方差的大小反映算法的稳定性[30]。将参数优化率定过程重复进行50 次,按目标函数取其最优值,每次都会得到一组最优的新安江模型参数以及目标函数值,总计50 组,统计分析每个参数和目标函数的方差,通过数据的离散程度判别GA、AGA 和IAGA算法的稳定性,结果如表5所示。
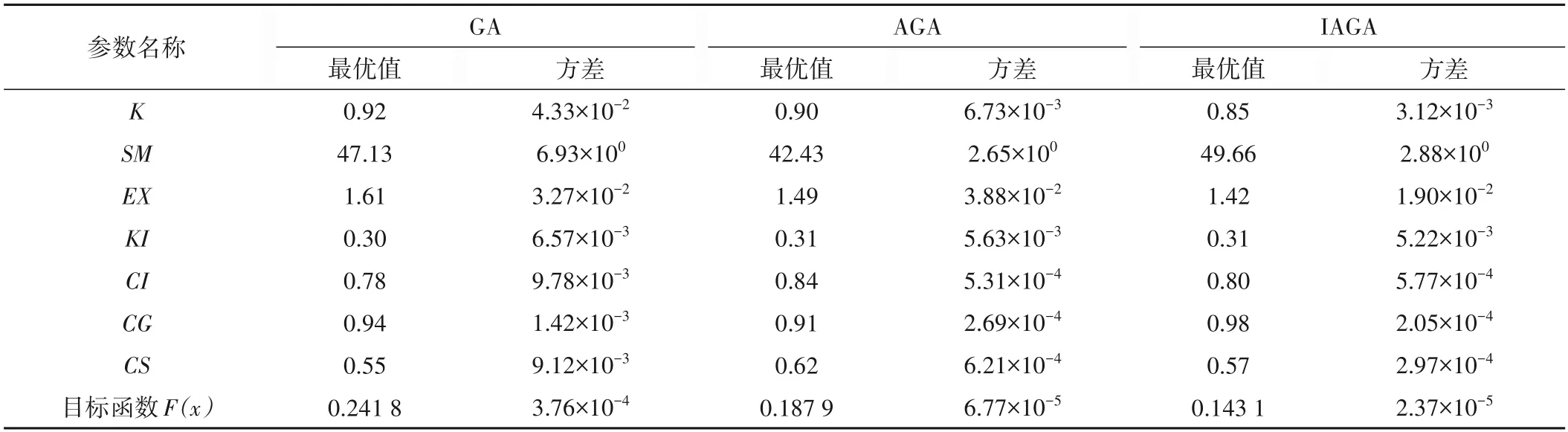
表5 参数K、SM、EX、KI、CS、CI、CG的自动率定结果Tab.5 Automatic optimization results of K,SM,EX,KI,CS,CI,CG
由表5 中的结果可以看出参数组优化结果并不稳定唯一,造成这样结果的很大一部分原因可能是“异参”同效作用的存在,同时不排除目标函数的选取单一,没有从整体上对各方面的模拟情况做约束等原因的影响。蒸散发折算系数K属于敏感参数,通常振幅较大,AGA 和IAGA 算法的率定结果的稳定性优于GA 算法,方差大小较为理想;自由水蓄水容量SM虽然数值波动较大,但是实际应用中分辨率较低,因此方差大小可以接受;自由水蓄水容量曲线指数EX存在波动,考虑到EX属于不敏感参数,因此异参同效现象比较明显,存在一定的波动属于正常现象;壤中流出流系数KI和河网水消退系数CS,3 种算法的率定结果相差不大,稳定性较为理想;壤中流消退系数CI和地下径流消退系数CG属于敏感参数,而且分辨率较高,AGA 和IAGA 的率定结果表现出良好的稳定性,远优于GA 算法。通过对各参数方差的分析,总体上率定稳定性IAGA>AGA>GA,主要是由于自适应交叉变异概率和自适应非均匀变异算子,在种群进化收敛的过程中,自适应减小交叉变异概率,保障优良基因的不被破坏,逐步缩小变异搜索范围,有利于算法稳定。对比多次率定后目标函数的方差,如图3所示,其结果与参数方差的分析结果保持一致,IAGA 算法的目标函数方差最小,说明其率定稳定性最优。
4.2.4 洪水模拟效果
算法的率定效果可以根据新安江模型对洪水的模拟误差来进行评价,表6 对场次洪水的模拟误差进行了统计,图4 展示了场次洪水的模拟效果。模拟效果的评价指标主要采用洪量、洪峰流量和峰现时间的相对误差、确定性系数(R2),以及纳什效率系数(NSE),根据《水文情报预报规范》分析各算法的预报精度,采用IAGA算法率定的10场洪水的洪峰流量、径流量均小于其许可误差,率定期和验证期的确定性系数均在0.85 以上,大部分场次洪水达到0.9 以上,纳什效率系数均在0.8 以上,部分场次洪水达到0.9 以上,总体预报精度均达到乙级水平。通过与GA 和AGA 算法对比,经IAGA 算法率定后的模拟效果更加接近实际洪水径流过程,GA 算法的偏离最大,AGA 算法次之,特别是20130702、20140629、20150614、20160627 和20180704 等场次洪水的洪量和洪峰的效果不理想,不合格率较高。据了解20160627场次洪水过程雨量洪量都较大,存在人为调度等因素,削减了实际洪峰,导致模拟结果中的洪峰计算值过大;20180814 场次洪水洪峰起涨前,受下游感潮河段水力联系影响,出现流量下降现象,导致模拟结果的洪水过程线整体偏大,增大了洪量和洪峰相对误差。率定效果表明IAGA 算法率定的秦淮河流域新安江模型参数基本上是合理的,并且效果优于传统的GA和AGA算法。

图4 场次洪水实测流量与模拟流量过程线Fig.4 Measured and simulated runoff of flood events
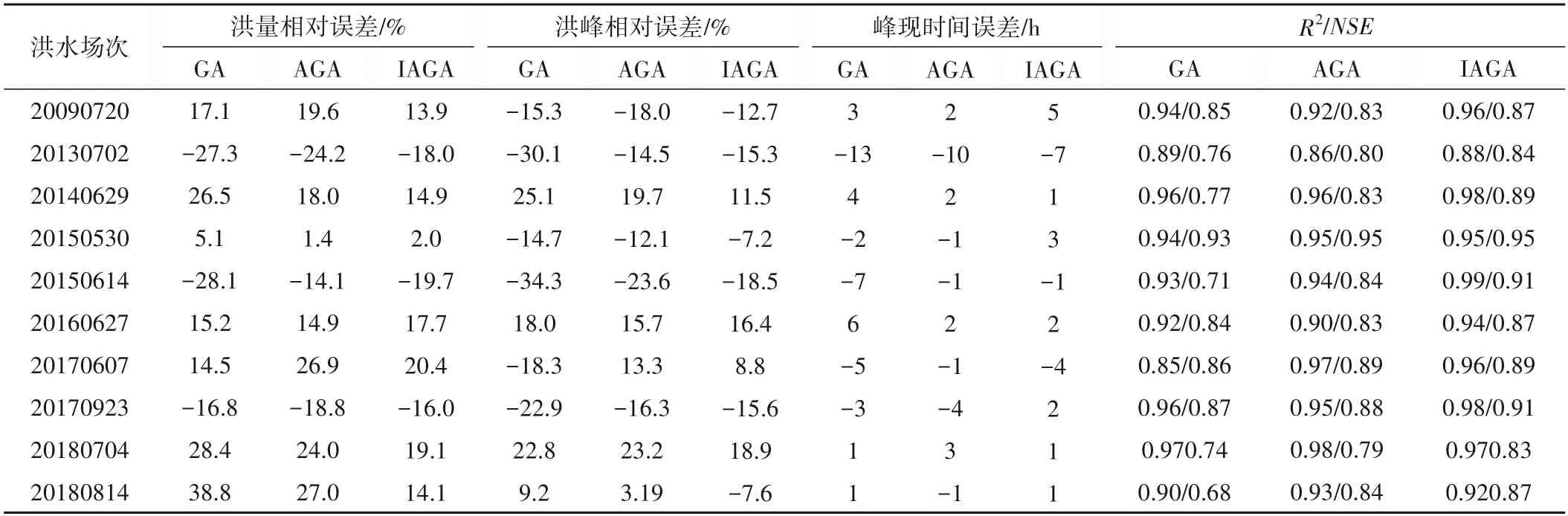
表6 秦淮河流域洪水模拟误差统计表Tab.6 Flood simulation errors of Qinhuai river basin
5 结论
针对新安江模型参数优化的特点,提出了一种改进的自适应遗传算法。该算法利用混沌优化的遍历性特点,提高了初始种群的个体质量;综合考虑种群进化程度和个体适应度两个维度,设计了自适应交叉变异概率算子,在种群进化初期,保证种群多样性,避免早熟,在种群进化后期,能够避免优良基因的破坏,保障稳定收敛;同时为加强局部重点区域的搜索,设计了自适应非均匀变异算子,根据种群进化程度,自适应的缩小优良个体变异的搜索范围,有利于进化收敛。以秦淮河流域为实例的场次洪水模拟结果表明,IAGA 算法的模型参数率定效果优于传统的GA 和AGA 算法,在率定的收敛性和稳定性方面具有较好的优势。由于IAGA 算法的复杂性,在耗时方面劣于传统算法,但是总体时间上能够满足应用要求,后期可以通过并行加速算法降低IAGA 算法的计算耗时。研究表明IAGA 算法能够克服遗传算法收敛过早、收敛不稳定、局部搜索能力弱等缺点,为水文模型参数率定提供了一种有效途径。
