I型加载模式下裂纹长度对压实黏土起裂机制的影响研究
2023-11-27王俊杰黄诗渊
吕 川,王俊杰,黄诗渊,罗 澳
(1.重庆交通大学河海学院,重庆 400074;2.重庆交通大学材料科学与工程学院,重庆 400074;3.重庆交通大学土木工程学院,重庆 400074)
0 引言
在高堆石坝建设中,由于坝壳料和防渗心墙变形模量差异,以及施工环境等因素的影响,心墙内部易形成裂缝[1]。作为常见的隐患之一,严重时将导致心墙发生水力劈裂,影响大坝正常运行[2]。因此,揭示土体的断裂机制对于保障工程安全具有重要意义。
针对土体的断裂问题,国内外学者开展了大量研究。LAKSHMIKANTHA 等[3]的研究结果表明土体断裂韧度受试样尺寸效应影响,同时与试验环境相关。刘晓洲和王悦东[4,5]对原状冻土进行了室内试验研究,构建了采用非线性修正因子计算原状冻土断裂韧度的方法。KONRAD 等[6]通过试验研究得出冻土断裂扩展受温度特征和水含量影响。为消除重力引起的试验误差,王俊杰等[7]提出了卧式加载方式。在此基础上,李泽华等[8]、邱珍锋等[9]探究了含水率和干密度对土体抗裂性能的影响,认为含水率和干密度对土体断裂韧度的影响显著。WANG 等[10]将岩石领域常用的单边切槽半圆弯曲试样引入压实黏土I 型断裂测试中,分析了断裂韧度随试样结构参数的关系,建立了通过抗拉强度评估断裂韧度的经验公式。秦鑫等[11]采用自研的试验装置测试不同含水量和土石比土梁试样的断裂韧度,得出土体断裂韧度随土石比的增大存在含水量奇异值,断裂韧度对土石比变化的敏感性高于含水率。
综上所述,研究人员各类型土体的断裂特性进行了试验研究和理论分析,为土体抗裂性能的研究奠定了基础。但现有研究集中于宏观力学性能的描述,尚未查明土体断裂机理。鉴于此,本次研究开展压实黏土I型断裂特性研究,查明预制裂纹长度对土体抗裂性能的影响规律,并结合数字图像相关方法从细观角度揭示其影响机制。
网络技术应用在电力调度信息化系统中,是为提高电力调度管理部门的工作效率,增强电力调度的安全性和时效性。网络技术与电力调度相结合有其既定的的原则:
1 试验方法
1.1 试验材料
试验用土为两河口水电站防渗心墙黏土,呈红褐色,塑限Wp=17.4%,液限WL=32.9%。最佳含水率和最大干密度分别为16.6%和1.75 g/cm3。黏土矿物成分以石英和黏土为主,分别占47.5%和41.9%。土料级配曲线如图1所示,试验前剔除2 mm以上粒径的土体。拌合用水取自实验室自来水。
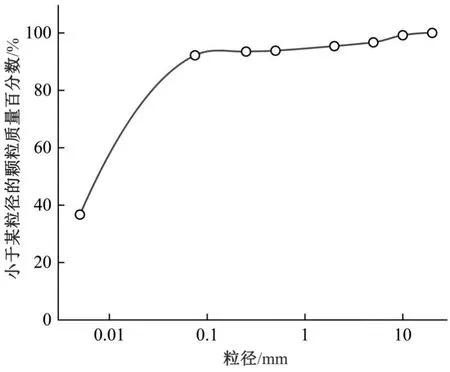
图1 级配曲线Fig.1 Grading curve
1.2 试样制备及试验方案
试样制备流程包括:①按照最佳含水率(16.6%)和最大干密度(1.75 g/cm3)计算试验用土和水的质量,拌合均匀后闷料24 h。②安装矩形钢模具,并在模具内部均匀涂抹凡士林。③将等分的土料均匀摊铺在模具内并击实,每层土的击实功应相同。④击实完成后的土体立即采用切割机分割为矩形梁,并对指定位置切割形成人工预制裂纹,裂纹宽度为1 mm。⑤用刷子在试样表面均匀涂抹一层白色水粉形成底膜,再喷涂黑色哑光漆形成随机分布的黑色斑点。
加载仪器采用重庆交通大学联合江苏永昌科教仪器制造有限公司研发的土体断裂测试装置,包括荷载传感器、位移传感器、压头、支撑销和数据采集软件。采用数字图像相关(DIC)方法研究土体断裂破坏过程,其基本原理是通过识别变形前后试样表面的散斑图像来获取变形数据的方法。采用相关系数C(p)表示不同时刻特征点的散斑图案匹配程度[13],计算公式见式(1)。图像采集及分析系统由光源(1 台)、工业相机(1 台)和图像分析软件(VIC-2D)组成。

图2 试样及其结构示意图Fig.2 Soil beam specimen and schematic diagram
1.3 加载和观测方法
加载方式为三点弯曲加载,试样结构为单边切口梁试样,尺寸为L×H×D=150×50×25 mm,如图2所示。ISRM 建议岩石材料I 型断裂试验的支撑点距离与试样长度比值S/L为0.5~0.8[12],确定本次试验的支撑间距S=120 mm。为探究裂纹长度对压实黏土起裂行为的影响,无量纲裂纹长度a/H取0.2、0.3、0.4、0.5和0.6。
式中:UT为试样发生破坏时累计吸收的总应变能,N/mm,即试样荷载-位移曲线的包络线面积,数值上等于荷载-位移曲线在横轴上的积分;D为试样厚度,mm;H为试样高度,mm;a为预制裂纹长度,mm。
对于上述问题,仍用“3个0.5相加”来解释显然是不对的.传统的小数乘法教学中,教师往往会忽略对于小数乘法意义的多方面理解.用单一模型讲解小数乘法的意义,会使学生陷入误区,同时对后续小数乘小数的意义理解形成影响.确切地说,学生不明白这种模型下为什么要用乘法,即3×0.5为什么表示“3的一半”!这一点在[4]中有较为详细的研究.
式中:P(x,y)是参考子区各点坐标的灰度值;P′(x0′,y0′)是目标子区各点坐标的灰度值;Pm和P′m分别为参考子区和目标子区的灰度平均值;p为描述变形前后图像子区位置和形状变化的变形参数矢量。
为进一步揭示预制裂纹长度对土体断裂破坏的影响机理,引入细观抗裂性能评价指标-水平应变密度DE,其表征了试样发生断裂破坏前起裂点所积蓄的总应变。DE计算公式如下:
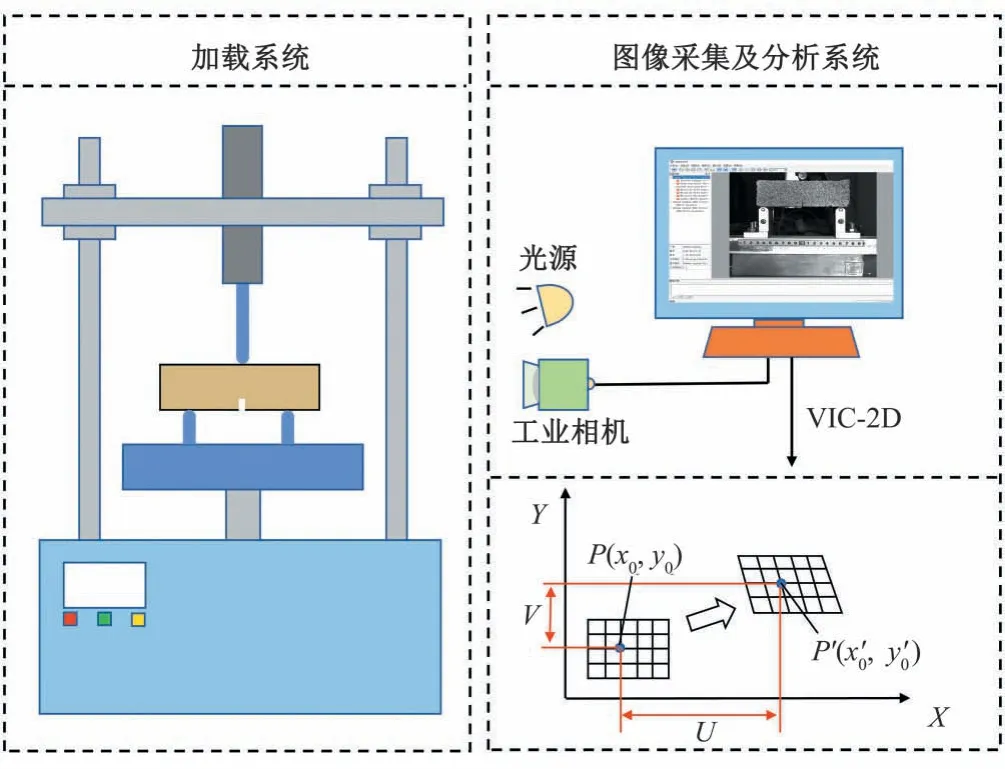
图3 试验装置Fig.3 Test setup
2 试验结果与分析
2.1 破坏模式
图4 为不同预制裂纹长度下试样的荷载-位移曲线。可以看出,预制裂纹长度不同时压实黏土的荷载-位移曲线具有相似的变化规律,大致分为3个阶段:①压密阶段。在轴向荷载作用下,试样支撑销与压头的接触位置首先产生局部压密,导致荷载-位移曲线产生一定程度波动;②线性变化阶段。试样内部萌生少量微裂纹,荷载-位移曲线呈线性递增,占曲线主要部分;③破坏阶段。达到峰值荷载后,荷载随位移的增加迅速降低,无黏性裂纹从预制裂纹尖端快速扩展。
春暖花开,春回燕来。京师气候不比江南,春脖子短,暮春如夏,到处生机盎然。像往年一样,李武岗不踏青,不郊游,只顾关起门来享受。那天,在拔火罐时,赤条条的他居然成为火人。比之已被烧死的李驷峋、李陆峰,李武岗烧得更彻底。据当时在场的仆人说,烧到半途,李武岗早就死去,火苗也已经弱下去,谁知躯干中间部位居然“突突”地喷出烈焰,将胸腹全部点燃,最终整个中段都烧没了,仅剩头颈和四肢。更诡异的是,就连易燃的丝质床单都未全部烧光,卧榻几乎完好无损。
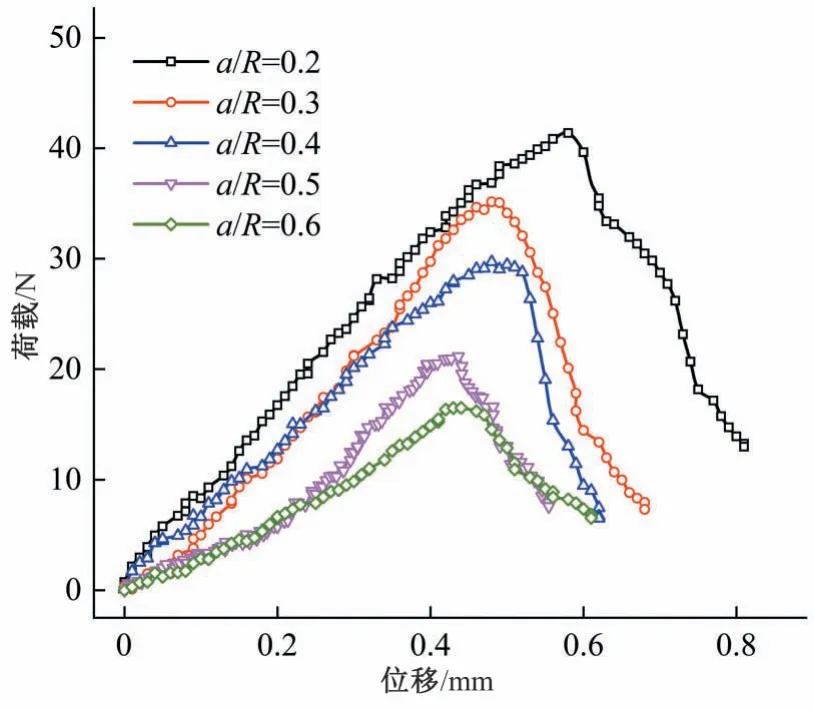
图4 荷载-位移曲线Fig.4 Load-displacement curve
式中:E(t)为EXX-时间的曲线函数;t0为峰值应变时刻对应的时间值;dt为时间微分。DE数值上等于图9 中区域S1与S2的面积之和。
通过DIC方法得到试件样断裂过程中的水平位移云图。以a/H=0.2试样为例,对土体断裂破坏过程进行分析。
2型糖尿病外周感觉神经病变和心脏自主神经病变存在相关性,进行感觉神经检查,可以评价心脏自主神经病变的风险。
加载至30%Pmax,如图5(a)所示,试样整体变形较小,底部土体产生相对侧移,预制裂纹顶部土体变形均匀。当荷载增加至50%Pmax和70%Pmax后,试样表面变形增大,底部的正向和负向位移区逐渐向上发展,形成连贯的位移等值线,如图5(b)和(c)所示。相比70%Pmax,90%Pmax时的水平位移云图形态差异更明显,水平位移值和位移梯度变化幅度增大,如图5(d)所示。图5(e)和(f)为Pmax和峰值荷载后90%Pmax时试样的水平位移云图。可以看出,预制裂纹尖端处的局部变形增大,导致位移等值线汇集。峰值荷载以后,裂纹发生不稳定扩展,无黏性裂纹长度逐渐增大。

图5 不同加载阶段试样的水平位移云图(单位:mm)Fig.5 Horizontal displacement clouds of specimens at different loading stages
2.2 临界断裂韧度
断裂力学理论采用临界断裂韧度JIC这一指标衡量材料的断裂能或应变能释放速率,是材料抗裂性能的评价指标。JIC数值越大意味着材料抗裂性能越好,其计算公式如下[14]:
验证标准偏差相对稳定,具有统计意义。2004年QSAR国际会议正式形成经济合作与发展组织(英文简称OECD)规则,明确必须使用外部验证集(即测试集)来评价模型的预测能力。如果样本量足够大,也可以从105个样本中随机取8个样本作为测试集,97个样本作为训练集。本案例执行该规范。
图6为不同预制裂纹长度下压实黏土试样的临界断裂韧度JIC。由图6 可知,随着裂纹长度增大,试样JIC呈线性递减变化。文献[15]对重庆黏土进行了试验,其结果与本研究规律一致。a/H=0.2 时,JIC最大,平均值为0.05 N/mm;a/H=0.6 时最小,平均值为0.025 N/mm,较前者降低了50%。随着轴向荷载逐渐增大,试样内部微裂纹在韧带区域内的萌生和汇集。预制裂纹较短时,试样具有较长韧带区,裂纹孕育区域面积相应增大,导致试样发生破坏时累计吸收的总应变能增大,使得土体具有较大的JIC。
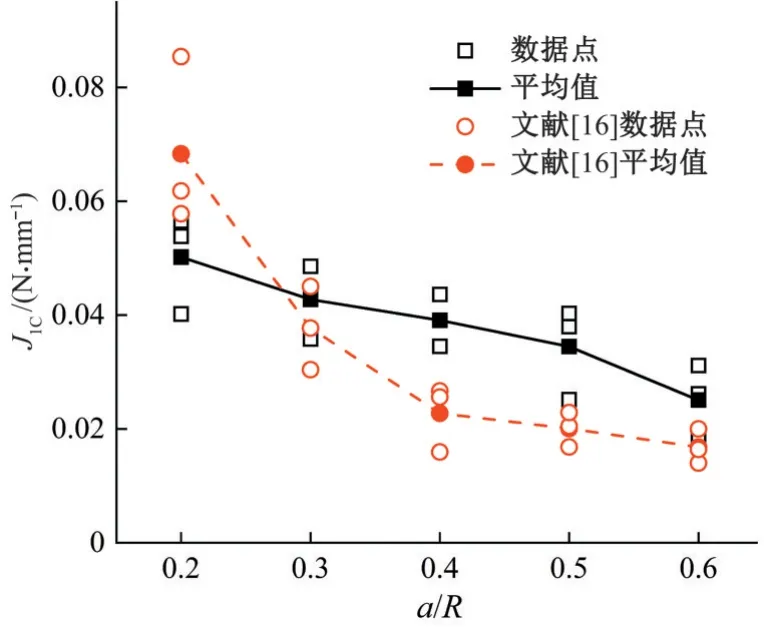
图6 JIC演化规律Fig.6 JIC evolutionary pattern
2.3 土体细观损伤特性
图7为不同预制裂纹长度试样在峰值荷载时刻的水平应变云图。由图7可知,试样发生破坏时,预制裂纹尖端产生较大拉应变,形成局部损伤区域,峰值应变随预制裂纹长度增大而减小。受边界效应影响,损伤区域形态发生改变。a/H为0.2~0.4时,韧带区域占比较大,损伤区呈圆形或椭圆形。当a/H≥0.5后,压头与试样接触区域的局部变形限制了损伤区向上发育,导致损伤区的宽高比较大。

图7 峰值荷载的水平应变云图Fig.7 Horizontal strain cloud at the peak load
以A、B 两点的水平应变EXX平均值作为压实黏土起裂点受荷全过程的EXX值,不同预制裂纹长度下起裂点EXX的演化规律如图8所示。可以还看出,预制裂纹长度对EXX演化规律影响不大。以a/H=0.2 试样为例进行说明,如图9所示。加载初期EXX增长缓慢,呈线性递增(S1区域)。该阶段土体表现为弹性变形,形成少量微裂纹。加载至一定时间后,EXX增长速率变大,出现非线性增长趋势(S2区域),表明试样内部裂纹产生和不断发育。达到峰值荷载后,微裂纹汇集形成宏观裂纹,导致EXX迅速增大(S3区域)。
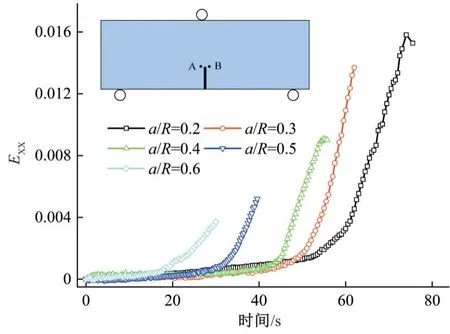
图8 EXX随时间的演化规律Fig.8 Evolutionary pattern of EXX with time

图9 荷载和EXX随时间的变化曲线Fig.9 Load and EXX curves with time
试验前,调整工业相机位置,保证相机镜头与试件表面垂直且精准对焦,并调整压头与试样顶部接触。加载与图像采集同时开始,加载速率选择0.6 mm/min,图像采集频率为500 ms/张。位移和载荷数据由计算机自动记录,试样破坏后停止采集。散斑图片导入VIC-2D 软件进行分析,获得目标区域内的位移数据。试验装置如图3所示。
随着预制裂纹长度增大,试样峰值荷载逐渐降低。a/H为0.2 和0.6 时的峰值荷载平均值分别为41 N 和14 N。最大轴向位移随a/H增大逐渐降低。上述规律表明土体破坏模式与预制裂纹长度无关,增大预制裂纹长度降低了土体的承载能力,对工程而言是不利的。
由式(3)计算出不同预制裂纹长度时土体的水平应变密度DE,其平均值结汇总于图10。由图10 可知,水平应变密度DE随预制裂纹长度增大逐渐递减。a/H=0.2 时DE最大,平均值为0.045 s;a/H=0.6 时最小,平均值为0.005 s,较前者下降了90%。这是由于韧带较短时,试样承载和变形能力降低所导致的。
基于语文学科的严谨性特点,要求初中语文教师在执行教学任务的过程中,要适当采取与学科教学特点配套的教学方式,以及采用丰富的教学语言来完善教学过程。如教师自身的教学专业词语概念要明晰,而且要避免频繁使用无意义的口头禅,课堂中的语言表达要尽可能做到精练。尤其是在语文课文课堂教学环节,教师要根据课文体裁的不同,选择不同的教学语言,进而与课文的题材相协调,促进教学质量的进一步提升。例如在教学散文时,教师要尽量选择抒情的语调,缓慢的语速和富有才情的语言,带领学生一同领略散文语言的优美。
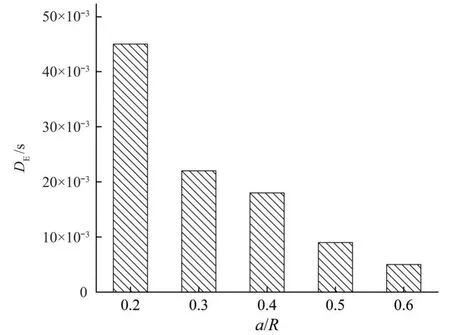
图10 不同预制裂纹长度时试样的DEFig.10 DE of specimens at different prefabricated crack lengths
对宏观力学指标JIC和细观评价指标DE进行拟合分析,如图11所示。临界断裂韧度JIC和水平应变密度DE具有良好的线性关系,表明采用JIC和DE评价预制裂纹长度影响下压实黏土抗裂性能的结论相符。此外,在拟合公式的基础上可采用临界断裂韧度对压实黏土的水平应变密度做出预估。
测量并记录两组患者HbAlc(糖化血红蛋白)、FPG(空腹血糖)、2 hPG(餐后 2 h 血糖)[3]。
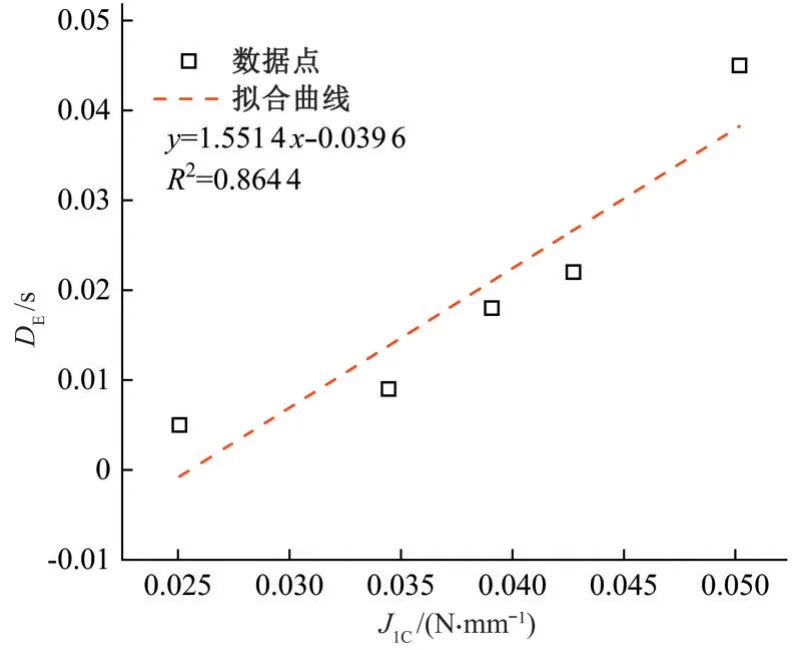
图11 宏细观抗裂性能评价指标的相关性分析Fig.11 Correlation analysis of macroscopic anti-cracking performance evaluation indexes
3 结论
为研究预制裂纹长度对压实黏土抗裂性能的影响,对单边切口梁试样开展I型断裂试验,结合数字图像相关方法,从宏细观角度分析了土体断裂机制,主要得出以下结论。
(1)土体破坏过程包括压密阶段、线性变化阶段和破坏阶段,破坏模式与预制裂纹长度无关;
(2)随着预制裂纹长度增大,试样临界断裂韧度JIC呈线性递减。
(3)峰值荷载前起裂点峰值水平应变呈线性递增和非线性递增两阶段变化,峰值荷载后迅速增大;
(4)水平应变密度DE随着预制裂纹长度增大逐渐降低,与临界断裂韧度JIC呈线性相关。
