速度—应力声波方程混合交错网格有限差分数值模拟及逆时偏移

胡自多，刘威，宋家文，曾庆才，田彦灿，韩令贺

（1. 中国石油勘探开发研究院西北分院，甘肃兰州 730020；2. 中国石油集团油藏描述重点实验室，甘肃兰州 730020；3. 东方地球物理公司研究院，河北涿州 072750；4. 中国石油勘探开发研究院，北京 100083）

0 引言

波动方程数值模拟是研究复杂介质中波场传播规律的重要手段［1-2］，是逆时偏移（RTM）［3-4］和全波形反演（FWI）［5-6］的重要基础。相比伪谱法［7-8］和有限元法［9-10］，有限差分法［11-12］具有计算效率高、占用内存小、算法实现简单灵活等优点，已发展成为应用最普遍的一种波动方程数值模拟方法［13-15］。然而，有限差分法利用差分算子近似波动方程中的微分算子，导致波场的传播速度与真实速度不相等，且不同频率的波场传播速度不同，即出现数值频散现象［16］。固有的数值频散严重影响有限差分法的模拟精度［17-18］，进而影响了RTM 和FWI 的精度［19］，因此，压制数值频散、提高模拟精度是有限差分法的一项重要研究内容。

构建更合理的差分算子和改进差分系数计算方法是提高有限差分法模拟精度的两条重要途径。Dablain［16］指出，高阶差分算子能够减小数值频散，提高模拟精度，但时间高阶差分算子会使内存占用和计算量显著增加。此后，学者普遍保持时间2 阶差分算子不变，通过设计更合理的空间差分算子以提高模拟精度。Fornberg［20］给出了基于泰勒级数展开的规则网格和交错网格2M阶（M表示空间差分算子中与差分中心点等距的坐标轴网格点的组数）空间差分算子的差分系数解析表达式，据此可以构建采用时间2 阶差分算子、空间2M阶差分算子的规则网格和交错网格有限差分法，本文称之为常规规则网格有限差分法（C-FD）和常规交错网格有限差分法（C-SFD）。CFD 和C-SFD 利用空间域频散关系和泰勒级数展开计算差分系数，尽管空间差分算子具有2M阶差分精度，但差分离散波动方程仍然仅具有2 阶差分精度。波动方程有限差分数值模拟通过迭代求解差分离散波动方程实现，不应通过分开逼近时间差分算子或空间差分算子达到高阶差分精度，而应该使差分离散波动方程达到高阶差分精度，才能有效提高有限差分法的模拟精度。针对二阶标量波动方程和一阶应力—速度声波方程有限差分模拟，一些学者提出基于时空间域频散关系和泰勒级数展开计算差分系数，构建了时空域规则网格和交错网格有限差分法，这种时空域有限差分法使得相应的二维和三维差分离散波动方程分别沿8 个和48 个传播方向达到2M阶差分精度，但沿其他传播方向仍然仅具有2 阶差分精度，呈现明显的数值各向异性［17，21］。除了上述基于泰勒展开的差分系数算法，基于最小二乘优化算法最小化频散关系误差，相速度误差和群速度误差求解差分系数也被广泛采用［22-24］，这种基于最小二乘的差分系数算法能够有效提高中高频成分的模拟精度，但会在一定程度上损失低频成分的模拟精度，并且最小二乘算法通过迭代优化差分系数，计算量较大。Liu［25-26］采用最小二乘优化相对空间域和时空域频散关系求解差分系数，将非线性最优化问题转化为线性最优化问题，求解过程不需要迭代，有效地提高了差分系数的计算效率。

仅通过改进差分系数算法提高模拟精度的效果有限，构建更合理的空间差分算子是有效提高模拟精度的另一重要途径。针对2阶标量波动方程，Liu等［27］提出了一种菱形网格有限差分法，并基于时空域频散关系和泰勒展开计算差分系数，使得差分离散波动方程沿任意传播方向达到2M阶差分精度，有效地提高了二维标量波动方程的模拟精度和稳定性，但是其空间差分算子长度随M2急剧增大，导致计算量巨大，计算效率低。后来，Wang 等［28］又提出组合常规十字交叉型网格和菱形网格以构建空间差分算子，有效兼顾了计算效率和模拟精度。胡自多等［29］借鉴频率域混合网格有限差分法［30-31］的构建思路，将波动方程中的Laplace 微分算子近似表示为直角坐标系中坐标轴网格点构建的Laplace差分算子和非坐标轴网格点构建的Laplace差分算子的加权平均，建立了一种混合网格有限差分法，它与Wang等［28］提出的有限差分法相似，但构建思路不同。胡自多等［32］导出了三维直角坐标系中非坐标轴网格点构建Laplace差分算子的方法，进一步构建了三维混合网格有限差分法，有效提高了三维标量波动方程的模拟精度和稳定性。针对速度—应力声波方程，Tan 等［33］提出联合利用坐标轴网格点和非坐标轴网格点构建空间差分算子近似波动方程中的1阶空间偏导数，建立了一种混合交错网格有限差分法，相应的差分离散声波方程可以达到4阶或6阶差分精度，有效提高了声波模拟精度。Ren等［34-35］进一步发展了这种混合交错网格有限差分法，使得差分离散声波和弹性波方程最高可以达到8阶差分精度。Zhou等［36-37］对混合交错网格有限差分法做进一步改进，使得差分离散声波和弹性波方程可以达到任意偶数阶差分精度，并采用两步线性优化方法简化了基于最小二乘的优化差分系数计算，进一步提高了声波和弹性波的模拟精度。然而，这类混合交错网格有限差分法不恰当地使用了非坐标轴网格点的对称性，通常将与差分中心点距离不相等的2组非坐标轴网格点赋予了相同的差分系数，导致难以推导差分系数的通解。

针对速度—应力声波方程数值模拟，本文发展了一种改进型的混合交错网格有限差分法（M-SFD），利用坐标轴网格点和非坐标轴网格点构建空间差分算子时，确保与差分中心点距离相等的1 组非坐标轴网格点赋予相同的差分系数，与差分中心点距离不等的任意2 组非坐标轴网格点赋予不同的差分系数，使得所构建的M-SFD 更为合理，并利用时空域频散关系和泰勒级数展开建立差分系数求解方程组，导出差分系数通解的解析表达式。

本文首先阐述了M-SFD 中空间差分算子的构建方法，给出相应的差分离散声波方程，并导出差分系数通解；其次，开展频散分析和稳定性分析；最后，利用层状介质模型和中国塔里木盆地典型复杂构造模型开展数值模拟，并将M-SFD 推广应用于RTM，利用塔里木复杂构造模型模拟数据开展RTM 测试。测试表明，该方法能够有效消除由于数值频散造成的成像假象，从而提高深层成像精度和分辨率。

1 混合交错网格有限差分法的基本原理

1.1 差分离散声波方程的导出

二维速度—应力声波方程可表示为

式中：P=P(x，z，t) 为压力场；υx=υx(x，z，t) 和υz=υz(x，z，t)分别为质点振动速度场的x和z分量；κ=κ(x，z)为体积模量；ρ=ρ(x，z)为介质密度。

交错网格有限差分法求解式（1）时，波场变量和弹性参数定义在交错的网格位置上，如图1 所示。波场变量P(x，z，t)差分离散点定义在空间x和z方向的半网格点、时间t方向的整网格点上（图1红色圆圈），其离散表达式为为整数，h为空间采样间隔，Δt为时间采样间隔。

图1 二维声波交错网格差分格式中波场变量及弹性参数相对位置示意图

与C-SFD 类似，M-SFD 采用时间2 阶差分算子近似式（1）中波场变量关于时间变量t的1 阶偏导数，可近似表示为

C-SFD 仅利用坐标轴网格点构建空间2M阶差分算子（图2a）近似波场变量关于空间的一阶偏导数，随着M取值的增大，新增网格点与差分中心点的距离也逐渐增大，对提高模拟精度的贡献逐渐减小。

图2 交错网格有限差分法的空间差分算子示意图

本文所提M-SFD的基本思路是：联合利用坐标轴网格点和非坐标轴网格点构建一种混合型的空间差分算子近似波场变量关于空间的1 阶偏导数。图2b～图2e为M-SFD（N=1、2、3、4）的空间差分算子示意图，N表示空间差分算子中与差分中心点等距的非坐标轴网格点的组数。相比C-SFD，M-SFD能有效利用距离差分中心点更近的非坐标轴网格点，理论上更合理。

本文提出的M-SFD 与Tan 等［33］提出的时间和空间高阶交错网格有限差分法具有一定的相似性，但是他们不恰当地使用了非坐标轴网格点的对称性，将与差分中心点距离不相等的两组非坐标轴网格点赋予了相同的差分系数，例如将图2d 中标记为绿色②和③的两组非坐标轴网格点赋予了相同的差分系数，标记为绿色②的网格点与差分中心点的距离为而标记为绿色③的网格点与差分中心点的距离为这种不合理的赋值导致差分系数的解析解求解困难。本文提出的M-SFD 给任意两组与差分中心点距离不等的网格点赋予不同的差分系数，理论上更合理，并且求解差分系数的解析解更容易。

M-SFD（N=1）与Tan 等［33］提出的时间4 阶、空间2M阶交错网格有限差分法本质上完全相同。下面以M-SFD（N=2）为例阐述M-SFD 的基本原理。利用图2c 中M-SFD（N=2）的空间差分算子近似方程（1）中波场变量关于空间变量x和z的一阶导数，可以表示为

式中am（m=1，2，…，M）、b1、b2均为差分系数。将式（2）和式（3）代入式（1）得到

式（4）为M-SFD（N=2）对式（1）的差分离散声波方程，同样还可以导出M-SFD（N=1、3、4）对式（1）的差分离散声波方程。

1.2 差分系数计算

合理的差分系数算法能有效提高交错网格有限差分法的模拟精度。C-SFD 利用空间域频散关系和泰勒级数展开计算差分系数，使得空间差分算子达到2M阶差分精度，但是相应的差分离散声波方程仅具有2阶差分精度［21］。交错网格有限差分法通过迭代求解差分离散声波方程实现声波数值模拟，为了提高模拟精度，应该设法提高差分离散声波方程的差分精度，而不是仅仅提高空间差分算子的差分精度。

M-SFD 基于时空域频散关系和泰勒级数展开计算差分系数，将有助于提高差分离散声波方程的差分精度。下面以M-SFD（N=2）为例，阐述M-SFD 的差分系数计算方法。均匀介质中，速度—应力声波方程（1）具有如下形式的离散平面波解

式中：AP、Aυx和Aυz为平面波的振幅；k为波数；θ为平面波传播方向与x轴正向的夹角；ω为角频率。

将式（5）代入式（4）得到

消去式（6）中的AP，Aυx和Aυz，并且考虑到ω=vk和κ=ρv2，得到

式中：v为介质中声波的传播速度rant条件数。

式（7）为M-SFD（N=2）给出的差分离散声波方程的频散关系，也称为时空域频散关系。泰勒展开其中的三角函数，得到

其中cj、βj和γj的表达式为

使式（8）左右两边k2xk2zh2的系数对应相等，得到

使式（8）左右两边k2xk4zh4（或k4xk2zh4）的系数对应相等，得到

使式（8）左右两边k2j+2xh2j（或k2j+2zh2j）(j=0，1，2，…，M-1) 的系数对应相等，得到

根据式（12）可得出c0=±1，当c0从1 变为-1，相应的差分系数为a1，a2，…，aM；b1变为其相反数，对最终结果没有影响。这里取c0=1，并进行计算和推导可以得到

由式（13）可知c0=1，c1=r2，将它们代入式（10）和式（11）并联立求解，可得到

将式（13）代入式（9）得到

式（15）可改写为如下矩阵方程

式（16）是一个范德蒙矩阵方程。

联合求解方程（14）和（16）得到

式（17）为M-SFD（N=2）的差分系数通解，利用同样的方法，可以导出M-SFD（N=1、3、4）的差分系数通解，见附录A。

1.3 差分精度分析

可以将差分离散声波方程的频散关系误差函数关于空间采样间隔h或时间采样间隔Δt的最小幂指数定义为差分离散声波方程的差分阶数。根据M-SFD（N=2）给出的差分离散声波方程的频散关系式（7），定义误差函数EM-SFD(N=2)，表达式为

结合式（8）～式（12），EM-SFD(N=2)可化简为

式（19）表明，EM-SFD(N=2)关于空间采样间隔h的最小幂指数为6，因此M-SFD（N=2）给出的差分离散声波方程具有6 阶差分精度。式（19）给出的EM-SFD(N=2)的表达式较为复杂，还可以从差分系数求解过程直接分析M-SFD（N=2）给出的差分离散声波方程的差分精度。根据M-SFD（N=2）的差分系数求解过程可以看出，EM-SFD(N=2)可以看成关于h的多项式，差分系数会使EM-SFD(N=2)中的系数均为零，EM-SFD(N=2)中系数不为零的最低次项为因此，M-SFD（N=2）给出的差分离散声波方程具有6阶差分精度。

同样地， M-SFD（N=1）给出的差分离散声波方程的频散关系误差函数EM-SFD(N=1)可以看成关于h的多项式，差分系数能够使得EM-SFD(N=1)中的系数为零，EM-SFD(N=1)中系数不为零的最低次项为和给出的差分离散声波方程具有4 阶差分精度；M-SFD（N=3）给出的差分离散声波方程的频散关系误差函数EM-SFD(N=3)可以看成关于h的多项式，差分系数会使得EM-SFD(N=3)中的系数均为零，EM-SFD(N=3)中系数不为零的最低次项为，因此M-SFD（N=3）给出的差分离散声波方程具有6 阶差分精度；M-SFD（N=4）给出的差分离散声波方程的频散关系误差函数EM-SFD(N=4)可以看成关于h的多项式，差分系数会使得EM-SFD(N=4)中0，1，2，…，M-1)，的系数均为零，EM-SFD(N=4)中系数不为零的关于h的最低次项为和因此M-SFD（N=4）给出的差分离散声波方程具有8 阶差分精度。理论上，继续增大N的取值，M-SFD 给出的差分离散声波方程可以达到任意偶数阶差分精度。C-SFD 给出的差分离散声波方程仅具有2 阶差分精度［21］，因此，M-SFD 能更有效地提高数值模拟精度。

表1 给出了当差分离散声波方程达到相同阶的差分精度时，本文的M-SFD 与Tan 等［33］构建的时间和空间高阶交错网格差分格式需要的非坐标网格点数。对比可以看出，达到相同阶的差分精度，本文的M-SFD 需要的非坐标轴网格点数更少，因而计算量更小，计算效率更高。

表1 相同阶差分精度本文方法与Tan 等（2014）方法所需的非坐标轴网格点数

2 频散分析和稳定性分析

2.1 频散分析

数值频散能直接反映交错网格有限差分法的数值模拟精度。本文引入归一化相速度误差函数εph(kh，θ)定量描述数值频散的大小。根据M-SFD（N=1）给出的差分离散声波方程的频散关系式（7）和相速度的定义的表达式为

εph(kh，θ)=0 时，相速度与真实速度相等，无数值频散；εph(kh，θ)>0时，相速度偏大，呈现时间频散；εph(kh，θ)<0时，相速度偏小，呈现空间频散。同理，可导出C-SFD 和M-SFD（N=2、3、4）的归一化相速度误差εph(kh，θ)的表达式。

图3 给出了不同M值时C-SFD 和M-SFD 的归一化相速度误差εph(kh，θ)随kh和θ变化的特征。可以看出：①M=2 时，C-SFD 呈现明显的空间频散，相速度误差达到-4.0%（图3a 左）；M增至5 时，空间频散明显减小，相速度误差最大为-1.5%，但出现较明显的时间频散，相速度误差最大为2.0%（图3b左）；M增至8，空间频散基本消失，时间频散进一步增大，相速度误差最大为2.0%（图3c 左）。②M=2时，M-SFD 呈现明显的空间频散，相速度误差达到-4.0%（图3a 右）；M增至5 时，空间频散明显减小，相速度误差最大为-3.0%（图3b 右）；M增至8 时，空间频散进一步减小，相速度误差最大为-1.0%（图3c 右）。③M取值较小时（如M=2），M-SFD 和C-SFD 均具有较严重的数值频散，模拟精度均较低；M取值较大时（如M=8），M-SFD 的数值频散明显小于C-SFD，因此M-SFD 的模拟精度优于C-SFD。④如果将数值频散误差的绝对值小于1‰定义为高精度。M的取值从2 增至8 时，C-SFD 的高精度模拟区域基本没有增大，而M-SFD 的高精度模拟区域逐步增大。M取值大于5 时，M-SFD 的高精度模拟区域明显大于C-SFD。⑤M的取值从2增至8时，C-SFD和M-SFD 的空间频散均逐步减小，说明增加空间差分算子中坐标轴网格点数有助于减小空间频散；M取值相同时，M-SFD 的时间频散均小于C-SFD，说明增加空间差分算子中非坐标轴网格点数有助于减小时间频散。

图3 不同M 值时C-SFD（左）和M-SFD（N=1）（右）相速度频散等值线图（r=0.3）

图4 给出了不同M及N时，M-SFD 的归一化相速度误差εph(kh，θ)随kh和θ变化的情况。需要注意M-SFD（M=10；N=1、2、3、4）和M-SFD（M=20；N=1、2、3、4）两组子图中等值线的刻度不同，色标代表的相速度误差范围也不同。可以看出：①M=10，N=1、2、3、4 时，M-SFD 的数值频散特征相似，基本能将相速度误差的绝对值控制在1‰以内（图4 左）。②M=20，N=1时，M-SFD 主要表现出时间频散，相速度误差最大为3.0‰（图4a右）；N增至2 时，时间频散显著减小（图4b 右）；N增至4 时，时间频散进一步减小（图4d右）；M=20，N=4时，M-SFD 基本能将相速度误差的绝对值控制在0.1‰以内（图4d右）。③对于一般的高精度模拟，要求将相速度误差的绝对值控制在1‰以内，建议采用M-SFD（N=1），M的取值为10 左右；如果对模拟精度要求极高，要求将相速度误差的绝对值控制在0.1‰以内，可以采用MSFD（N=4），M的取值约为20。因此，M-SFD 应根据模拟精度要求，合理选择M和N的取值以兼顾计算效率。④固定M的取值，N的取值为2 和3 时，MSFD 的相速度误差分布规律基本一致，这是因为此时M-SFD 给出的差分离散声波方程均为6阶差分精度，见表1.

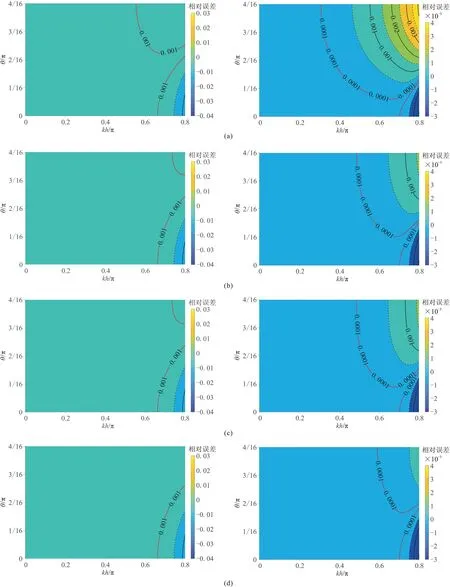
图4 M=10（左）及M=20（右）时不同N 值的M-SFD 相速度频散等值线（r=0.3）

2.2 稳定性分析

根据M-SFD（N=2）给出的差分离散声波方程的频散关系式（7）得到

式中S为稳定因子。

式（22）为M-SFD（N=2）给出的差分离散声波方程的稳定性条件表达式。同样地，可以导出C-SFD和M-SFD（N=1、3、4）的稳定性条件表达式。图5 给出了稳定性条件约束下，r的最大取值随M的变化曲线，称为稳定性曲线。可以看出：①C-SFD 和M-SFD（N=1、2、3，4）的稳定性均随M取值的增大而降低；②M取值相同时，M-SFD（N=1、2、3，4）的稳定性强于C-SFD；③固定M取值，M-SFD 的稳定性会随N取值的增大而增强，因此，增加空间差分算子中非坐标轴网格点数能增强稳定性；④N的取值为2 和3 时，M-SFD 的稳定性完全相同，这是因为M-SFD（N=2、3）给出的差分离散声波方程均为6 阶差分精度，见表1。

图5 C-SFD 和M-SFD（N=1、2、3、4）的稳定性曲线

3 数值模拟实例

3.1 层状介质模型

图6给出了一个包含5个反射界面的层状介质速度模型，模型尺寸为12 km×12 km，模型空间采样间隔h=15 m，网格数为801×801。震源采用主频为22 Hz 的Ricker 子波，位于（0.15 km，0.15 km）。CSFD（M=12）采用时间采样间隔Δt=0.5、1.0 ms；M-SFD（M=10；N=1）采用Δt=1.5 、2.0 ms；MSFD（M=10；N=2，3，4）采用Δt=2.0 ms 进行模拟。图7 和图8 分别给出了C-SFD 和M-SFD（M=10；N=1）模拟得到的3.6 s 时刻压力场P和质点振动速度场x分量υx的波场快照。图9a给出了M-SFD（M=10；N=2）模拟生成的单炮记录。为对比方便，图9b 和图9c 分别为C-SFD（M=12）和M-SFD（M=10；N=1，2，3，4）采用不同时间采样间隔模拟生成的炮集记录中第781道不同时间区间范围内的波形对比。

图6 层状介质速度模型

图7 不同参数C-SFD（上）及M-SFD（下）层状介质3.6 s 时刻压力场（P）模拟波场快照

图9 M-SFD 层状介质模型模拟炮集记录（a）和两种方法不同时区单道波形对比（b）及其放大显示（c）

表2 统计了C-SFD（M=12）和M-SFD（M=10；N=1，2，3，4）采用不同时间采样间隔进行模拟的耗时和加速比，模拟总时长为9.0 s，且均采用Inter Xeon Gold 5218 CPU 处理器。

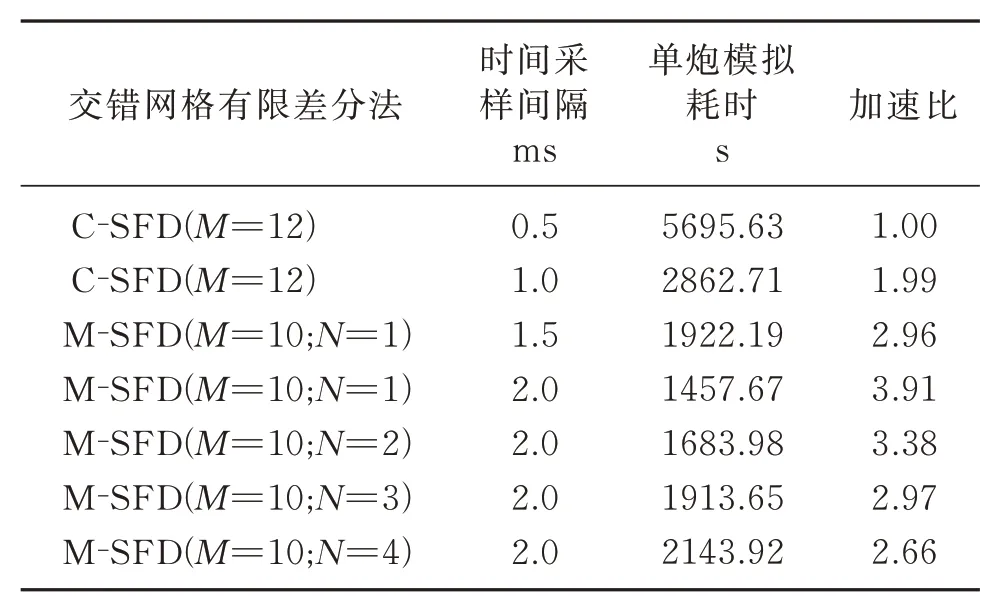
表2 C-SFD 和M-SFD 法层状介质声波模拟的耗时和加速比对比

图7和图8中两组波场快照显示：C-SFD（M=12）采用Δt=0.5 ms进行模拟的波场快照中无明显数值频散，当时间采样间隔增至Δt=1.0 ms时，波场快照中出现明显的时间数值频散；M-SFD（M=10；N=1，2）采用Δt=2.0 ms进行模拟得到的波场快照均无明显数值频散。

图9b和图9c中的单道波形显示：C-SFD（M=12）采用Δt=1.0 ms进行模拟，波形畸变严重，采用Δt=0.5 ms 进行模拟，波形仍存在一定程度的畸变；MSFD（M=10；N=1）采用Δt=2.0 ms 进行模拟，波形存在一定程度的畸变，采用Δt=1.5 ms进行模拟，波形仅存在微小畸变；M-SFD（M=10；N=2，3，4）采用Δt=2.0 ms进行模拟，波形畸变基本可以忽略，模拟波形与参考波形基本重合。

综合图7～图9 给出的数值频散特征及表2 给出的计算效率统计结果，可以看出：M-SFD（M=10；N=1）采用Δt=1.5 ms比C-SFD（M=12）采用Δt=0.5 ms 模拟的数值频散更小，精度更高，且计算效率提高了1.96 倍；M-SFD（M=10；N=2）采用Δt=2.0 ms 比M-SFD（M=10；N=1）采用Δt=1.5 ms模拟，数值频散更小，精度更高，且计算效率更高。

仔细对比图9c 中的单道波形会发现，采用相同的时间采样间隔Δt=2.0 ms，M-SFD（M=10；N=3）与M-SFD（M=10；N=2）的模拟精度基本一致，M-SFD（M=10；N=4）相比M-SFD（M=10；N=2，3）在模拟精度方面存在十分微弱的优势，需要在更长传播距离和传播时间的情况下，这种优势才能更好地体现出来。

3.2 复杂构造模型

图10a 为中国塔里木盆地典型复杂构造速度模型，模型尺寸为18 km×7.875 km，模型空间采样间隔h=15 m，网格数为1201×526。震源采用主频为25 Hz 的Ricker 子波，位于（9 km，0.15 km），C-SFD（M=10）和M-SFD（M=8；N=1）分别采用时间采样间隔Δt=1.0 ms 和Δt=1.5 ms 进行模拟。C-SFD（M=10）和M-SFD（M=8；N=1）的空间差分算子均包含20 个网格点，单次时间迭代的计算量基本相同，模拟时长相同时，计算效率与时间采样间隔成正比。

图10 中国塔里木盆地典型复杂模型及声波交错网格有限差分数值模拟单炮记录（压力场P）

图10b 给出了M-SFD（M=8；N=1）采用采Δt=1.5 ms 模拟生成的单炮记录。为了对比方便，图10c～图10f 给出了C-SFD（M=10）和MSFD（M=8；N=1）不同时间采样间隔模拟生成单炮的局部放大显示。对比可以看出：C-SFD（M=10）采用Δt=1.0 ms 和Δt=1.5 ms 模拟生成的单炮记录中均存在明显的时间频散；M-SFD（M=8；N=1）采用两种Δt模拟生成的单炮记录中均无明显数值频散。

复杂构造模型模拟结果表明：计算效率基本相同时，M-SFD 比C-SFD 能更有效地压制数值频散，模拟精度更高；M-SFD 可采用更大的时间采样间隔以提高计算效率，并保持更高的模拟精度。

4 混合交错网格有限差分法在逆时偏移中的应用

将M-SFD 作为逆时偏移算法中的波场传播算子，以图10a 中的复杂构造模型进行逆时偏移测试。震源采用主频为25 Hz 的Ricker 子波。C-SFD（M=15）采用非常小的时间采样间隔Δt=0.1 ms，模拟生成150 炮无数值频散的炮集资料作为逆时偏移的输入道集，每炮600道接收，炮间距120 m，道间距30 m。

分别以C-SFD（M=10）和M-SFD（M=8；N=1）作为逆时偏移算法中的波场传播算子，时间采样间隔Δt=1.5 ms，采用互相关成像条件，并对成像结果做Laplace 滤波去除低频噪声。图11 给出了C-SFD（M=10）和M-SFD（M=8；N=1）的逆时偏移剖面。对比可以看出：C-SFD（M=10）的偏移成像结果中，深层同相轴存在大量由于数值频散造成的成像假象；M-SFD（M=8；N=1）的偏移成像结果中，由于数值频散造成的成像假象消失，深层同相轴能量更强，分辨率更高。因此，相比C-SFD，M-SFD 作为逆时偏移的波场传播算子能有效提高深层构造的成像精度和分辨率。

图11 中国塔里木盆地典型复杂构造模型声波混合交错网格有限差分RTM 剖面

5 结论

本文联合利用坐标轴网格点和非坐标轴网格点构建空间差分算子近似波场的一阶空间偏导数，建立了适用于速度—应力声波方程模拟的M-SFD，并基于时空域频散关系和泰勒级数展开导出了差分系数通解。通过差分精度分析、频散分析、稳定性分析、数值模拟和逆时偏移试验，得到以下结论：

（1）C-SFD 给出的差分离散声波方程仅具有二阶差分精度，M-SFD（N=1、2、4）给出的差分离散声波方程可达到4、6、8阶差分精度，继续增大N的取值，理论上可以达到任意偶数阶差分精度；

（2）计算效率基本相同时，M-SFD 比C-SFD 能更有效地压制数值频散，模拟精度更高；M-SFD 可通过采用更大的时间采样间隔以提高计算效率，且模拟精度仍然高于C-SFD；

（3）M-SFD 作为逆时偏移的波场传播算子能够更有效地消除数值频散造成的成像假象，进而提高深层的成像精度和分辨率。

附录A M-SFD（N=1，3，4）的差分离散声波方程及差分系数通解

与文中M-SFD（N=2）的差分系数求解过程类似，利用M-SFD（N=1）对声波方程（式（1））进行差分离散可以导出相应差分离散声波方程，再将离散平面波解代入差分离散声波方程导出相应的时空域频散关系，并利用泰勒公式对频散关系中的三角函数进行级数展开，然后，使得方程左右两边的系数对应相等以构建关于差分系数的方程组，求解此方程组可以得到M-SFD（N=1）的差分系数a1，a2，…，aM；b1的通解为

利用泰勒公式对M-SFD（N=3）给出的差分离散声波方程的时空域频散关系中的三角函数进行级数展开，然后，使得方程左右两边0，1，2，…，M-1)的系数对应相等以构建关于差分系数的方程组，求解此方程组可以得到M-SFD（N=3）的差分系数a1，a2，…，aM；b1，b2，b3的通解为

利用泰勒公式对M-SFD（N=4）给出的差分离散声波方程的时空域频散关系中的三角函数进行级数展开，然后使得方程左右两边或的系数对应相等以构建关于差分系数的方程组，求解此方程组可以得到差分系数a1,a2,…,aM;b1,b2,b3,b4的通解为