增广Lagrange方法求解二阶锥约束变分不等式问题

刘雨，孙菊贺，王莉，米娜，袁艳红

（1. 沈阳航空航天大学 理学院，沈阳 110136；2. 太原理工大学 经济管理学院，太原 030002）

考虑二阶锥约束变分不等式问题［1］：找到x*∈K，满足不等式

其中

mi≥1，m1+m2+…+mp=m，并且其中κmi，i=1，2，…，p是一个mi维的二阶锥。

变分不等式问题被广泛应用于优化问题、工程技术、力学、计算机科学、运筹学、运输业等诸多领域，引发了许多学者的特别关注。关于变分不等式问题的理论、应用和数值方法的研究一直在持续的进行。在主动配电网无功优化模型中， Yang等［2］采用了二阶锥松弛方法和区间优化理论进行求解，不仅可以极大地提高效率，而且还能使结果具有一定的稳定性。对于一定扰动下的约束轨迹问题的优化，Sun等［3］将原问题看作二阶锥的优化问题，通过使用连续的迭代算法来验证所提供的轨迹是否可行，同时也可以验证是否是最优轨迹。Jin等［4］提出了一种基于分解迭代二阶锥规划的零展宽鲁棒波束的形成方法，解决了非平稳状态下自适应波束形成性能下降的问题，同时也提高了复杂环境中自适应波束形成的鲁棒性。文献［5］在解决下层问题时，也利用了凸二阶锥规划问题对鲁棒约束进行了转化。Wu等［6］应用光滑算法来求解变分不等式的问题，并且证明了该算法的稳定性。石翔宇［7］研究一类二阶偏微分方程及位移障碍变分不等式问题的有限元方法，使用了插值与投影定理相结合的处理方法，降低了解的正则性的要求，探讨出了在不同条件下解的收敛性与超收敛性。Singh等［8］构造了求解多时间型变分不等式问题的迭代算法，并证明了其收敛性。Nnakwe等［9］研究了一种惯性效应的投影算法，使算法的序列无限逼近变分不等式问题和不动点问题的公共解，以此来解决一些非线性优化问题。

基于此，本文利用增广Lagrange方法［10］来求解一类二阶锥约束变分不等式问题。通过投影定理及变分不等式和优化问题的内在联系得到了二阶锥约束变分不等式问题不同等价变换形式。利用增广Lagrange函数构造了一类数值算法，并证明了数值算法的全局收敛性。最后将非精确牛顿法作为子算法求解了三个数值算例，验证了其可行性。同样增广Lagrange方法也有诸多应用，Han等［11］通过增广Lagrange法高效求解混合整数线性规划（MILP）公式。Feng等［12］提出了一种在不计算奇异值的情况下，基于增广Lagrange乘子的奇异谱分析去噪方法。同样Wang等［13］建立了增广Lagrange乘子的存在性，文献［14］也给出了更加一般结果。

定义1假设Rm空间有一向量s，记作s=，其中=(s1，s2，…，sm-1)∈Rm-1。那么二阶锥κm⊂Rm有如下定义：

对于任意的两个变量x=(x0；)∈R×Rm-1，∈R×Rm-1，则x和y的Jordan积［15］定义如下

对于∀x=(x0；)∈R×Rm-1具有以下的谱分解

式中：λ1和λ2是x的谱值，并且

式中：ω∈Rm-1，‖ω‖=1。用记作向量x在κm上的投影，则

其中[λi]+=max{0，λi}，i=1，2。显然

1 问题转化

对于问题（1）可以将其转化为如下的二阶锥优化问题［17］：

式中：f(y)=，并且f(y)≥0。则问题（7）得Lagrange函数为：

式中：y是原始变量；λ是对偶变量。由于x*是f(y)的最小值，因此在正则的条件下，(y，λ)是L(x*，y，λ)的一个鞍点，即∀y∈Ω，λ∈κ，有

式（9）通过不等式做差，有如下的等价表达式

由于Ax-b显然是可微的，那么系统（10）就意味着(x*，λ*)解决了如下变分不等式问题［18］，

∀y∈Ω，λ∈κ。根据投影算子的性质，上述变分不等式系统（11）等价于下列方程组问题

由于Ax-b是凸的，对于∀y∈Ω，可以得到（12）的等价形式

容易验证，式（9）～（13），在投影算子性质的作用下是相互等价的。

2 增广Lagrange法

设x1∈Ω是初始解，λ1∈κ是对应的La‐grange乘子，假设已知第k次迭代xk∈Ω和λk∈κ，那么第k+1步迭代有如下表达式

式中：α＞0，并且

是式（7）的一个增广Lagrange函数［17］。

需要注意的是xk+1同时出现在（14）式的左右两边，那么这就意味着式（14）是一个隐式方程。因此，求解隐式方程式是解决问题的关键。

根据投影算子的性质，式（14）可以等价为如下的变分不等式问题：

下面，将证明增广Lagrange算法（14）的全局收敛性定理［19］。

定理1假设问题（1）的解集Ω*是非空的，并且F是一个单调映射。令Ω⊂Rn是一个闭凸集，且α＞0。那么由增广Lagrange方法产生的序列xk依范数收敛于二阶锥约束变分不等式问题（1）的解。

证明：令式（16）中y=x*，再将新式子带入至式（17）中，可以得到

由此

根据式（19）中等式约束Ax-b是凸的，式（19）中最后一项可以等价为

因此结合式（19）～（20）有

令y=xk+1带入到式（13）的第一个不等式中，有

通过对式（21）与（22）的求和，可得

令λ=λ*带入到（17）式中，通过和=0，可得

由于F(x)是一个单调算子，通过式（23）与（24）可以推导出

对于任意变量x1，x2和x3，他们之间存在如下关系式

并且有

通过（27）式，将（25）式变形为

对式（15），从k=0到k=N进行累加求和

从不等式（29）可知，点对集{(xi，λi)：i=1，2，…，}的轨迹是有界的，如式（30）所示

并且它的级数也是收敛的，

因此当k→∞，由于序列(xk，λk)是有界的，因此存在一个元素(x'，λ')，当i→∞时，使得xki→x'和λki→λ'，同时

令（16）和（17）中k=ki，通过取极限i→∞可以得出

综合上述，式（33）与式（10）所表示关系是一致的。当x'∈Ω，λ'∈κ，有

因此序列(xk，λk)的任何极限点都是二阶锥约束变分不等式问题（1）的解，由此可以看出序列是单调递减的，因此其极限点是唯一的。即，当k→∞时，xk→和，因此和=λ'：=λ*。

3 数值模拟

由于增广Lagrange方法中的方程式是隐式的，当Ω=Rn的情况下，增广Lagrange方法（14）可化简为

式中：

非精确牛顿法

步骤1：令ξ0=xk，选取非负参数列{ηj}，并且j=0；

步骤2：若Gk(ξj)=0，停止；令xk+1=ξj；

步骤3：选取Hj∈∂Gk(ξj)，计算搜索方向dj∈Rn，满足

步骤4：令ξj+1=ξj+dj，并且j=j+1，转到步骤2。

本节将用非精确牛顿法作为子算法的增广Lagrange法求解当Ω=Rn情况下的数值算例。利用拟牛顿法通过令xk+1=ξj去找到第k次迭代的近似解，满足下述条件

此时ε1=10-7，下面将通过Matlab编程进行数值实验［22］。

例1 考虑下面变分不等式问题

式中：F(x)=并且b=0，F(x)是一个单调算子。

在此算例中，令ε0=10-9，ε1=10-7，α=0.4并且ηj=(j=0，1，2，…)，在非精确牛顿法中的第j次广义雅克比Hj的具体表达式为

接下来计算Bj，设

Bj的第一行元素有如下表达式

Bj的对角元素(i=2，3，…)有如下表达式

Bj的第一列元素有如下表达式

最后计算Bj中的其余元素，有

数值计算结果汇总见表1，其中k表示测试的迭代次数，Times表示测试第二次终止的时间。

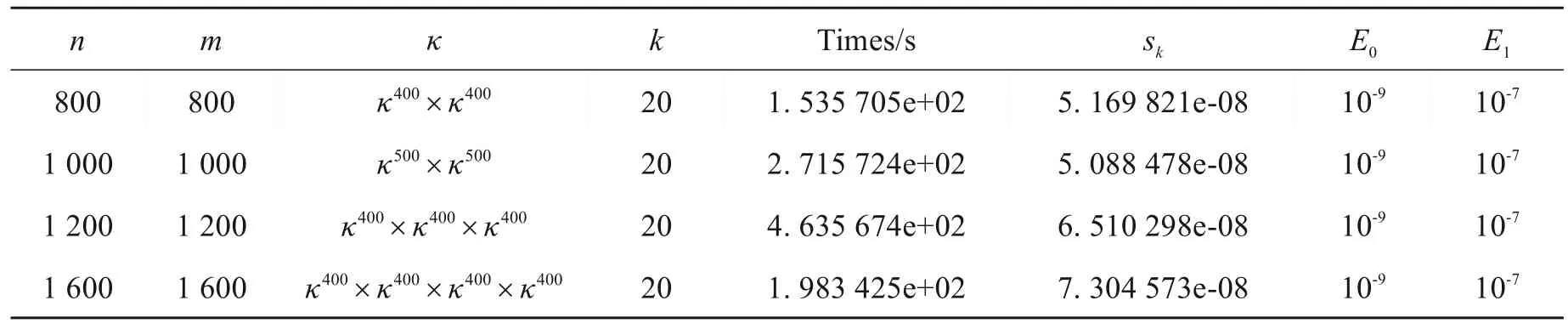
表1 关于例1问题的数值模拟结果

为验证算法的可行性与有效性，在同等精度下，利用增广Lagrange法与参考文献［17］中的算法做比较，文献［17］中算法结果如表2所示，不难发现增广Lagrange法迭代次数更少，具有一定的优势。

表2 文献中的数值模拟结果

参考文献［15］中，对于算例1也使用了增广Lagrange方法，但广义雅克比的Hj的表达式是放到正卦限中研究，而不是在二阶锥中研究，对此有表2的模拟结果。经过表2与表1的对比，不难发现利用改进的增广Lagrange方法，迭代的次数更少，结果更稳定。

例2 考虑下面变分不等式问题

式中：M是一个正半定矩阵，在此算例中，ε0=10-9；ε1=10-7；α=0.4；且ηj=(j=0，1，2，…)。在非精确牛顿法中的第j次广义雅克比Hj的具体表达为

数值计算结果汇总如表3。

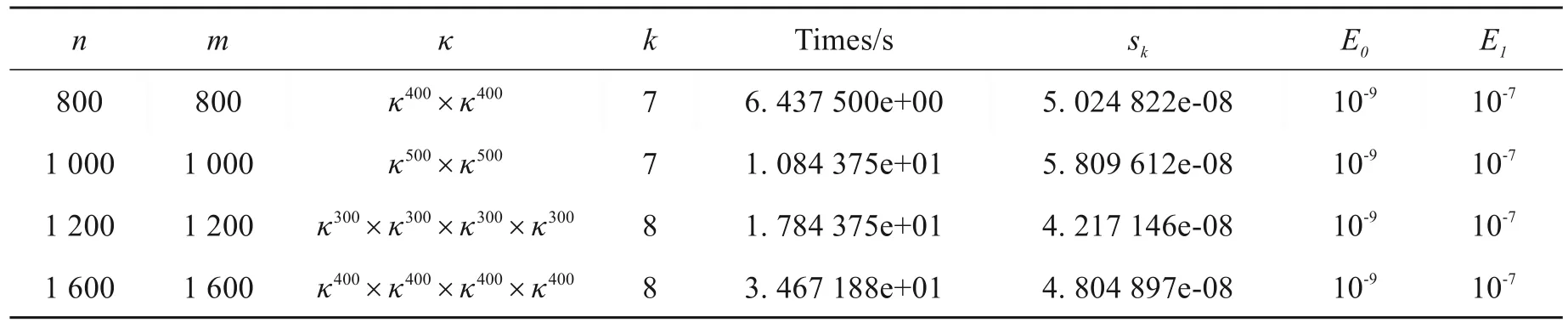
表3 关于例2问题的数值模拟结果

例3 考虑下面变分不等式问题

数值计算结果见表4。

表4 关于例3问题的数值模拟结果

4 结论

本文是基于Lagrange函数，将二阶锥约束变分不等式问题转化为二阶锥优化问题。通过讨论二阶锥锥优化问题一系列的等价形式，构造了一种求解二阶锥约束变分不等式问题的增广Lagrange方法。本文从实际的角度出发，考虑Ω∈Rn的特殊情况，即将Lagrange法迭代公式转化为方程组，并用非精确牛顿法进行求解。本文针对三个数值算例进行了数值模拟，并根据数值结果证明了增广Lagrange法的可行性与有效性。