基于GMM训练与HMM变换的波纹管振动信号分析
2023-11-24赵亚文范剑红陈金国涂志松曹存岚张玉龙
赵亚文,范剑红,陈金国,涂志松,曹存岚,张玉龙
(莆田学院 a.新工科产业学院;b.机电与信息工程学院,福建 莆田 351100)
引 言
当户外管道设备发生故障时,设备维修人员需要快速修复因温度、位移、压力及振动等各种复杂的环境因素引起的设备故障[1]。如果不及时控制,整个生产体系就可能面临崩溃,会引发一系列的生产停滞,危及工业设备运行的可靠性,降低设备的正常工作效率。波纹补偿器是用来补偿工业管道因各种复杂的环境条件而出现故障的装置,但是监测波纹管的工作状态却是主要的技术难题。
数字量可以直接观测并确定波纹管的损坏程度,并找出故障的临界点。然而,根据加速度传感器输出的模拟量却无法提供有关波纹管振动故障的信息。同时,振动信号的幅值和频率也会随着故障类型、位置和波纹管磨损程度的不同而变化。在多数情况下,振动对波纹管的损害严重且难以判断,因此波纹管振动信号分析对于管道行业是至关重要的研究领域。首先,需要使用采集仪器和加速度传感器收集正常和异常工作条件下的波纹管振动信号。然后,粗略记录不同情况下波纹管故障的类型和位置。最后,需要进一步分析和处理采集到的振动信号,从而准确监测波纹管的故障情况。
在振动信号分析方面,本文提出了一种改进的方法,该方法是基于高斯混合模型(Gaussian Mixture Model,GMM)训练[2]和隐马尔可夫模型(Hidden Markov Model,HMM)变换[3]的振动信号分析方法。HMM变换是一种功能强大的动态识别算法,适用于对动态时间序列问题进行模拟。由于波纹管长期处于户外振动条件下工作,并且波纹管的动态情况无法直接通过主观判断得到[4-6],因此需要间接分析振动信号来获取工作状态值。同时,与传统的故障诊断方法相比,基于GMM-HMM 的故障诊断方法[7]具有更好的模型泛化性能和更短的模型训练时间,从而表现出更优异的故障诊断效果。
1 波纹管振动信号采集实验及分析
1.1 信号采集
为了研究波纹管振动工作状态,需对波纹管进行振动实验。实验中加速度传感器型号是CA-YD-106,Zigbee 模块作为下位机把采集的信号利用无线网技术发送到另一个Zigbee 模块,分别测量出波纹管在损坏与正常条件下的振动信号,在采集电脑上输出并进行存储。振动信号采集流程及实物图分别如图1(a)、1(b)所示,振动信号接收与发送过程如图2所示。
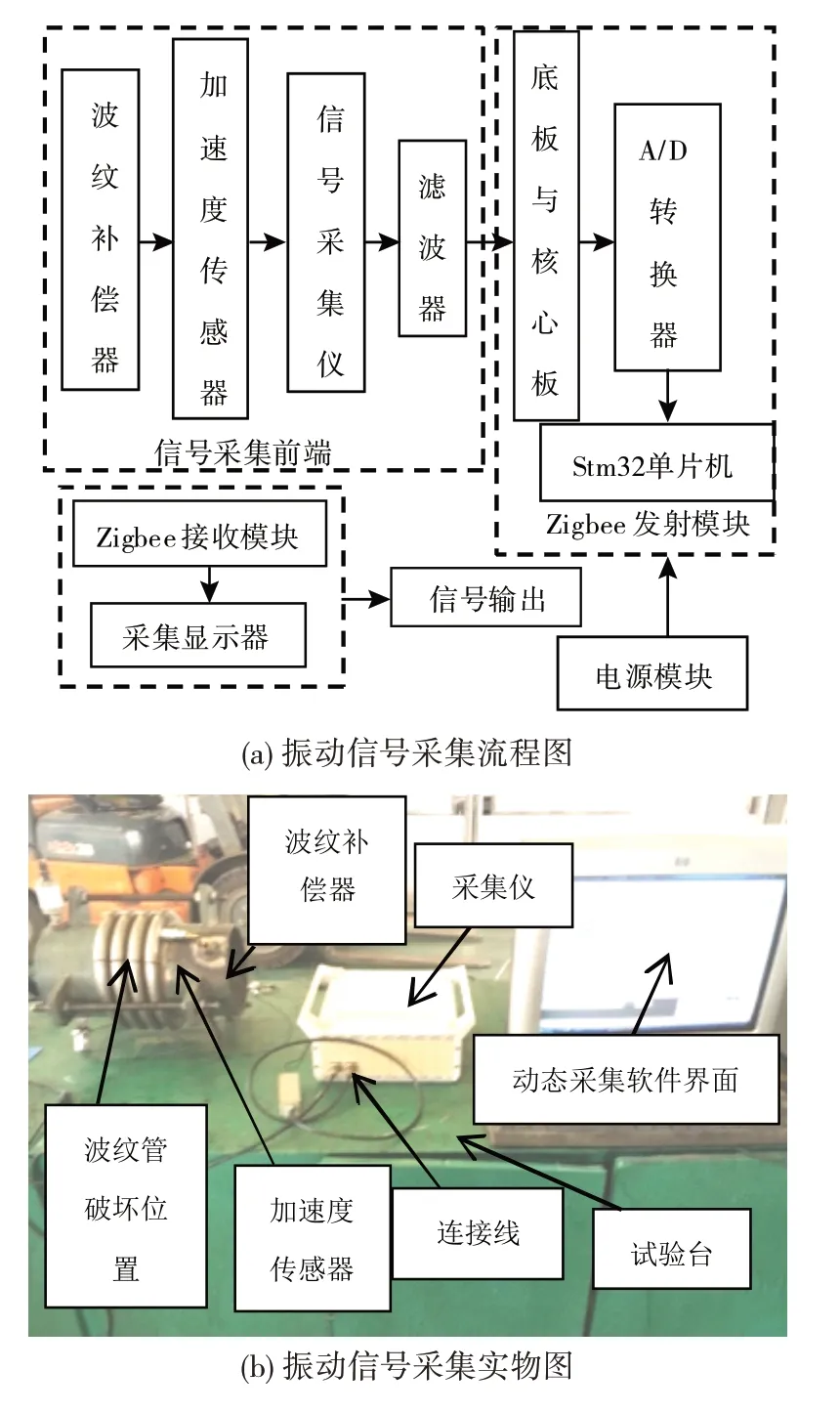
图1 振动信号采集图
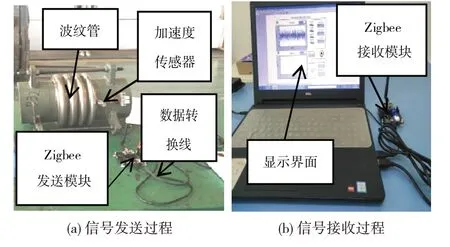
图2 振动信号发送与接收过程
1.2 信号预处理
本实验利用打磨工具多次磨损波纹管,其波纹管的磨损位置如图3所示。
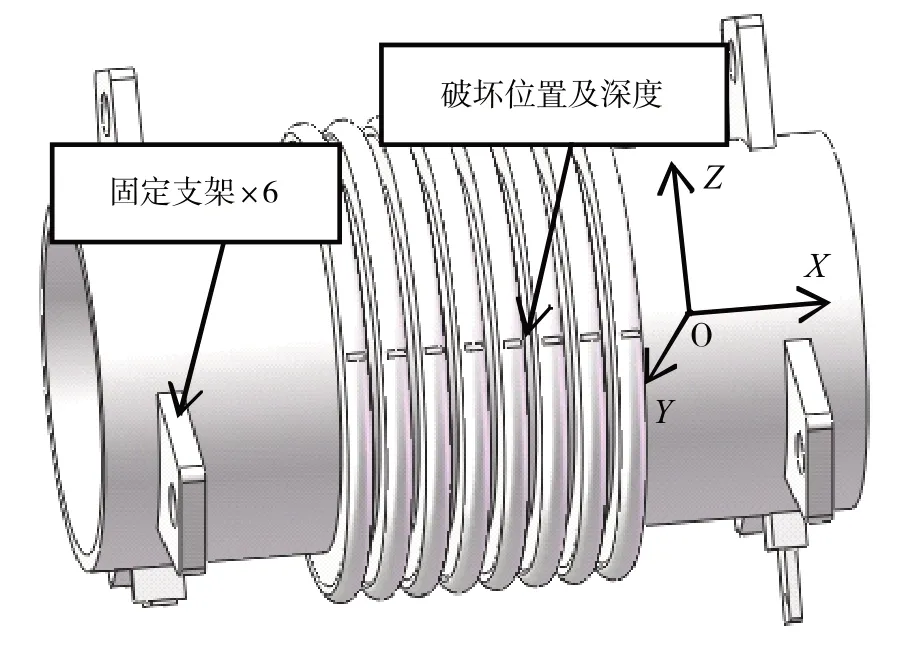
图3 波纹补偿器的磨损位置仿真图
图3 中的波纹管磨损位置已标注显示,设置其磨损深度分别为0、0.4、0.8、1.2 mm。为了减少数据误差,测量时,加速度传感器的固定位置为波纹管轴心的X方向,垂直轴心向外为Y方向,垂直轴心向上为Z方向。由于加速度传感器采集的信号是动态模拟量,故其数据时域值见表1~3。
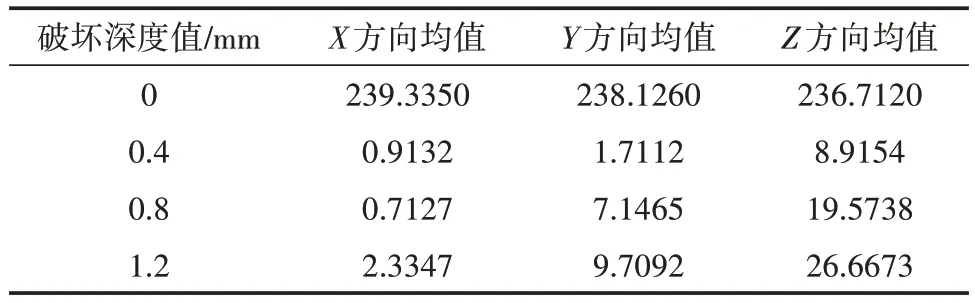
表1 波纹补偿器3个方向均值
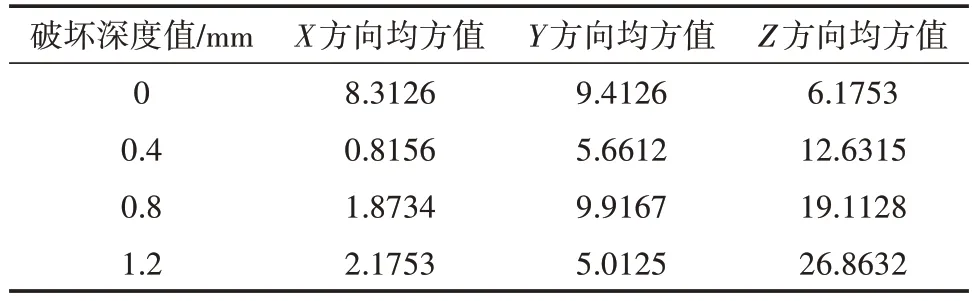
表2 波纹补偿器3个方向均方值
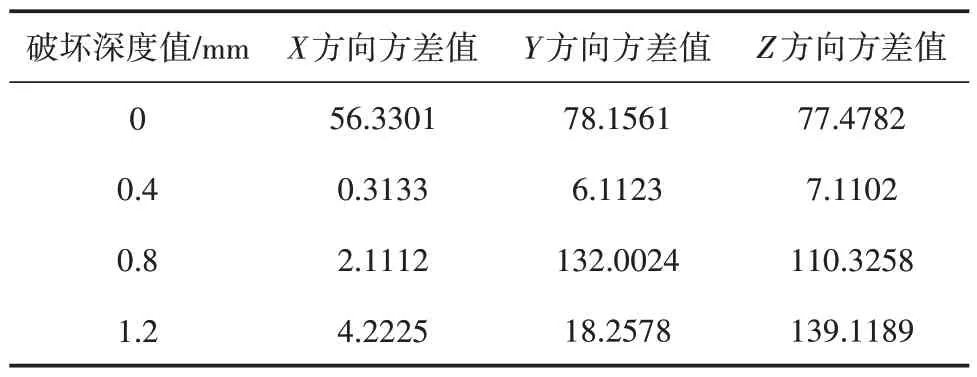
表3 波纹补偿器3个方向方差值
据表1~3 中数据可初步判断,当波纹管无磨损时,3 个方向的时域幅值稳定在240.0000 左右;发生磨损时,其均值、均方值、方差值落差明显,其变化趋势如图4 所示。从图4 中虽可初步得知发生故障,但时域分析并不能从根本上确定波纹管随着其破坏深度的增加而发生故障的机率,故存在可估性,需要对振动数据进行GMM 训练与HMM 变换处理,对其进行准确辨析。
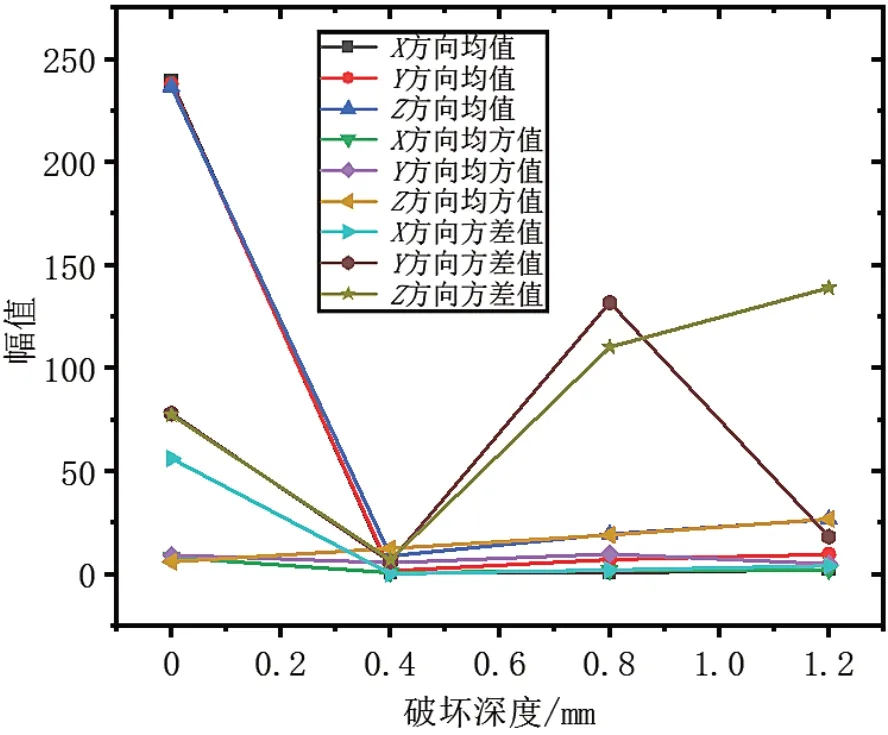
图4 波纹补偿器振动信号时域值
2 GMM训练算法的信号分析
2.1 振动信号的GMM算法训练
振动信号来源于波纹管上加速度传感器运行期间的数据流,其采样频率为每秒采样一次。
由于振动数据量十分庞大[8],而且极难对直接得到的振动数据进行分析利用,振动数据的异常表现不直观且无法得知是否发生异常振动。为此,需要对采集振动数据进行GMM 序列展开。将波纹管有磨损的信号与无磨损信号展开,分别如图5(a)、5(b)所示。
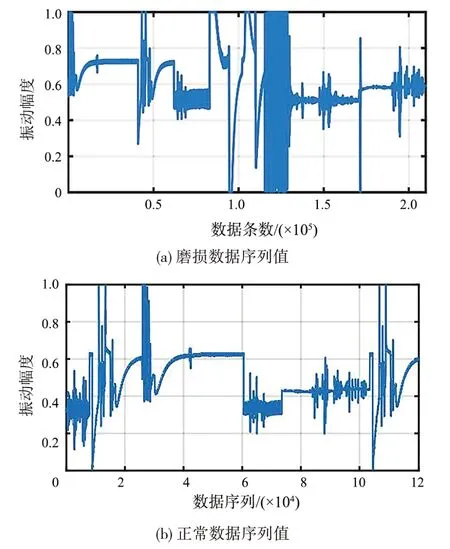
图5 振动信号磨损与正常序列值
振动数据采用最小二乘法回归拟合数据的处理方法进行分析处理[9-10]。将波纹管采集的振动数据进行分区,采用213 256 条振动数据作为训练数据,将每个分区的数据量设定为2500条,共有85个分区。
对于图5 中异常和正常的训练数据输入,进行一维数字滤波器滤波降噪处理。使用最小二乘法将每个数据分区拟合成一条线段。将所有数据分区拟合线段的斜率和端点差值的数据保存,并绘制每个数据分区的斜率-端点差值分布图,如图6所示。

图6 分区斜率-端点差值分布
当数据区数在20~30 之间时,图6 中可以明显看出斜率接近于零,即平稳状态,且端点差值变化小。当数据区数在30~35 之间时,斜率突然出现极端峰值,具有上升与下降趋势,而端点差值无明显的变化。用斜率-端点差值的方法可以清晰看出数据分区线段的变化趋势,其振动数据存在明显的上升或下降情况,据此可通过分析某一分区数据变化对斜率-端点差值的影响来判断波纹管在实际运行过程中是否发生故障。从图6 还可以明显看出,振动数据包含急速下降、轻微下降、平稳、轻微上升和急速上升5 种状态,同时将这5 种状态作为波纹管工作过程中的观测状态。由于上述5个振动数据的变化趋势会出现误差影响,故需对聚类GMM 高斯混合模型进行最优化处理。
2.2 构建聚类GMM高斯混合模型
聚类高斯混合模型[11]通过将数据拟合成一系列多维的高斯分布函数来实现,其具体的分布情况如下。
假设样本数据有一些n维数据如L={l1,l2,…,ln};而算法模型需要去寻找到最能够表示L的K个高斯分布T1,T2,…,TK。其中Tk是以μk为均值,εk为协方差矩阵的正态分布:
这K个高斯分布中每个分布都有一个贡献权重πk,故可以得到:
使得:
其中,P(lj)为高斯分布概率;p(lj/Tk)为高斯条件概率。
这个概率密度函数是Tk的加权和。而对于给定的最优取值数据L,μk、εk、πk为未知,为了解决这个问题,若已知样本lj由某个分布Tk产生,可以对它的概率进行推理:
由此可以计算出所有的Tk加权和为:
假设l的实现是独立的,由此可得:
式中N为模型隐含状态的个数。
GMM 高斯混合模型需要选择模型参数πk、Tk、与最大化式P(L)或者找到等价的对数似然度即式(6)。GMM 高斯混合模型利用计算简单且质量有保障的方法来寻找这个最优值:期望最大化(Expectation Maximization,EM)算法去寻找局部最大,EM 算法在每次迭代过程中,需计算每个高斯分布对每个样本的影响,然后优化高斯参数的估计并重新生成聚类结果。
如果数据L有μk、εk的估计值,且k=1,…,K,混合模型算法可以计算lj属于第k个高斯分布的概率:
这是给定Tk中lj的概率与lj的总体概率的比值,乘以当前权重值πi,这里定义:
式(8)是pjk在整个数据集上的均值,同理,可以估计相应的μk、εk的值:
EM 算法是机器学习十大算法之一,是求目标函数最大值的算法,通过期望最大算法不断迭代数据的μk、εk值,且更新高斯函数参数直至收敛,生成的高斯分布可以真实拟合数据L。
3 HMM算法的信号分析
3.1 隐马尔可夫模型
隐马尔科夫模型转换如图7 所示,通常选用五元组λ=(N,M,H,A,B)表示[12-13],其中,M表示每个隐含状态观测值数量;H为各初始状态概率的n维向量;A为状态转移概率矩阵;B为观测概率矩阵。
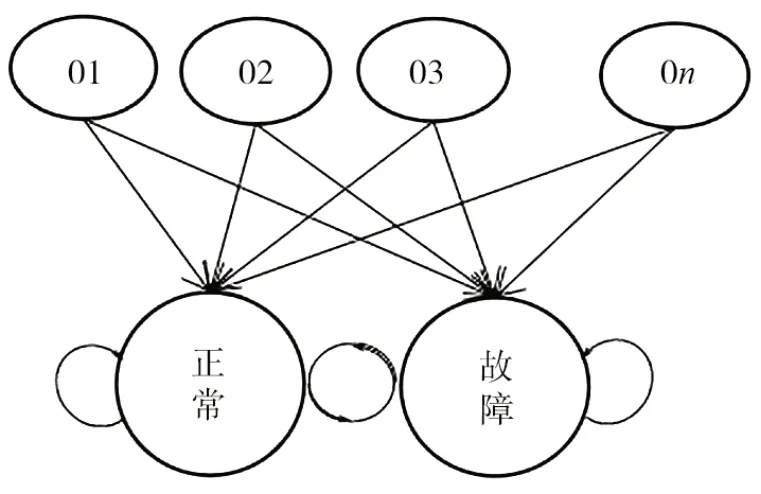
图7 HMM状态转换图
一个HMM通常要解决3个问题。
1)模型评价问题:给定模型和观察序列,计算实际产生观察序列的概率。
2)解码问题:对给定模型和一个观察序列出现的可能序列进行预测。
3)学习问题:训练隐马尔科夫模型最优模型参数问题。
隐马尔可夫模型通过初始状态产生随机序列。利用聚类GMM 结果,初步确定HMM 的状态转移矩阵和观测概率矩阵。通过多次训练随机序列,估计实际的状态转移矩阵和观测概率矩阵,同时使用Viterbi算法估计数据序列的隐藏状态。通过观测序列的后验概率输出结果,判断波纹管当前工作状态是否发生故障。
3.2 信号训练过程
对训练数据所有分区数据的斜率-端点差值数据绘制散点图并进行K-means 聚类分析,其中K-means 聚类中心个数设定为5,聚类结果如图8所示。
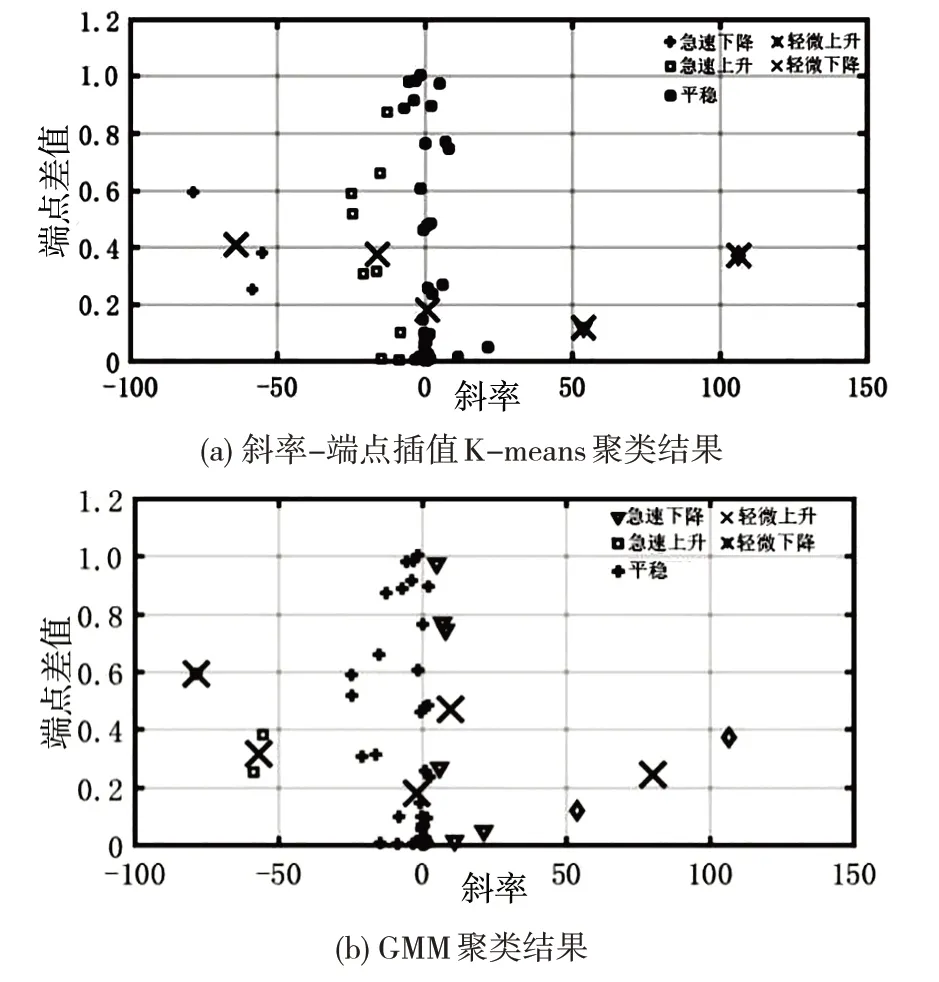
图8 训练数据聚类结果图
从图8 中K-means 聚类结果,可以看出振动数据的5 种分布状态情况,且K-means 聚类结果的5种状态与从斜率-端点差值得到的结果类似,同时可以得出5种状态下具体的数据分区个数,见表4。

表4 数据分区线段分布K-means聚类结果
从表4 中的聚类结果可以看出,波纹管在整个工作过程中,整体呈平稳振动。聚类结果需重点分析不平稳变化过程中的波纹管故障。由于K-means均值聚类算法的局限性,聚类结果对于孤立的数据点值非常敏感。例如,在图8(b)急速上升状态中,该算法只能发现球状聚类,这意味着聚类结果存在差异较大的斜率现象。
改进的聚类方法使用聚类高斯混合模型,将K-means 聚类结果作为高斯分布函数初始值,且设定μk、εk,使用EM算法估计参数,更新迭代得到新的聚类GMM聚类,其结果见表5。

表5 GMM聚类结果
经过GMM 优化聚类后消除原来急速上升孤立点的影响,聚类结果经过EM 算法多次迭代更新更具可靠性[14]。对GMM 聚类中心保存的数据分析,聚类结果中存在部分轻微下降与轻微上升的问题,这里认定上部分端点差值大类别为轻微上升,而将下部分端点差值小类别认定为轻微下降。将这5种可能的观测状态作为隐马尔可夫模型的观测状态,即急速下降、轻微下降、平稳、轻微上升、急速上升,分别用1、2、3、4、5 来表示这5 种状态。根据GMM 聚类结果可以初步估计HMM 参数,训练前的HMM 模型的参数矩阵为:
根据得到的观测序列多次训练估计真实状态转移矩阵和观测概率矩阵,训练后的HMM 模型的参数矩阵为:
利用Viterbi 算法,结合状态转移矩阵和观测概率矩阵,可以估计观测序列所对应的隐藏状态序列,以判断是否发生故障。在解码HMM 中的观测序列输出后,可以将后验状态概率作为判断结果的依据。
3.3 信号测试过程
为了测试HMM 模型性能,在相同的条件下收集了一组包含12 万条振动数据的样本。对经过滤波处理后的测试数据进行分片,并运用最小二乘法来回归拟合这些数据线段。记录线段的斜率和端点差值数据,如图9(a)所示。将测试分区数据与GMM 聚类中心进行计算分类,生成的观测序列如图9(b)所示。将观测序列导入已训练好参数的HMM中,利用Viterbi算法估计观测最有可能的状态序列。输出隐藏状态序列结果如图9(c)所示,输出观测序列的后验状态概率分布如图9(d)所示。
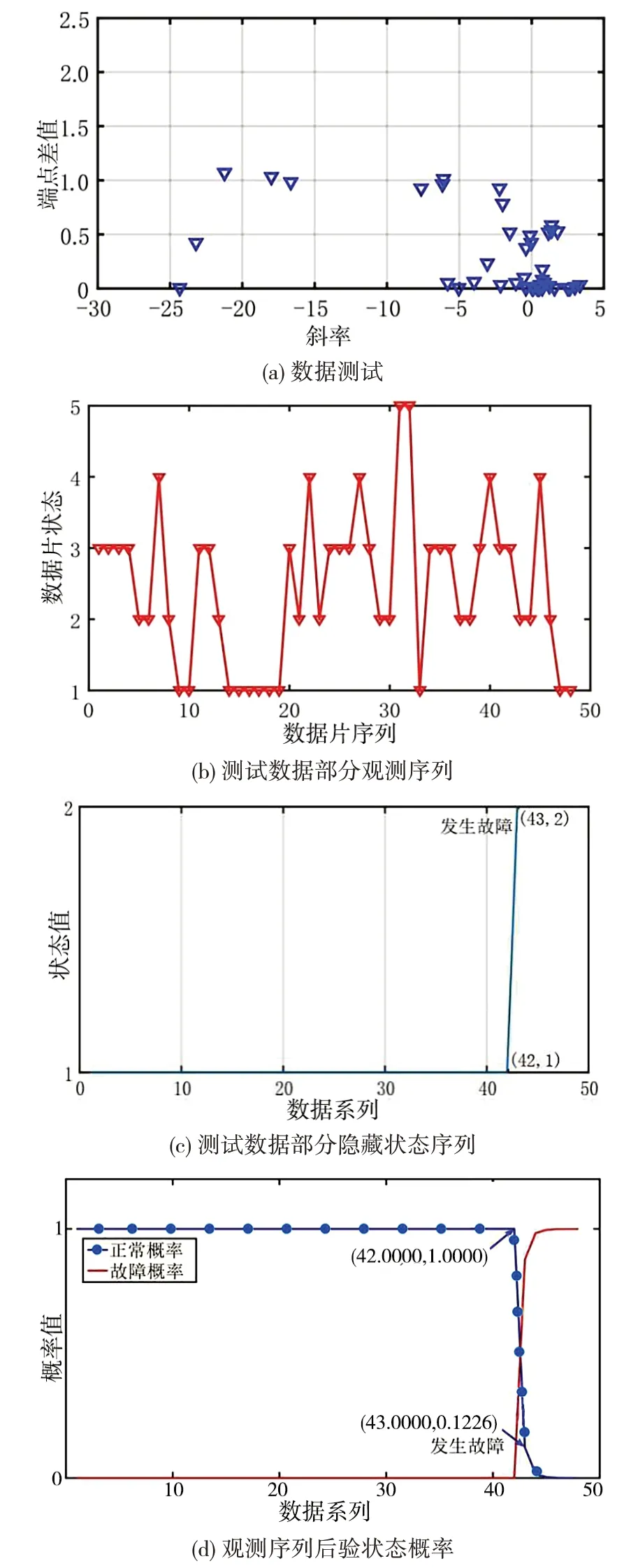
图9 数据测试处理结果
观测序列经HMM 模型分析并输出隐藏状态和对应后验概率数据,图9(d)中的结果表明在第41 分区波纹管工作状态由正常转变为故障。
4 基于GMM-HMM的故障诊断
从3.3 节中可知,一般的HMM 模型并没有特定的实际应用场景进行优化,若直接采用HMM 模型进行故障诊断,则有可能出现与实际情况不符合的现象,导致判断错误,为此需要对Markov 链类型与观测值概率转移矩阵进行特定的改进与优化[15]。
1)Markov链类型
HMM模型的Markov链均为各态经历型,因此波纹管的工作状态并不会实现工作状态的任意转移,而会朝着某个方向进行不可逆的工作状态演变。
2)观测值类型
对于普通的HMM 模型而言,采集的振动数据为固定的离散数据值,即为离散型HMM。但对波纹管的工作状态来说,HMM模型的观测值是通过特定的方法从原始振动数据中提取的振动特征。这就直接导致了HMM 模型的观测值是连续变化的,故无法采用固定离散的转移矩阵来描述振动数据的状态,而解决方法为通过概率密度函数对连续转移概率观测值进行描述。经过大量测试,效果良好。
本论文基于GMM-HMM 的故障诊断方法,对波纹管振动信号进行了分析,该方法的诊断思路是通过对异常和正常数据进行离散训练,主要实现数据特征提取和GMM-HMM 模式训练。然后,将经过训练的数据输入到GMM-HMM 故障诊断模型库中,计算故障诊断结果概率密度。现采用同样的方法采集多组振动数据的数据量,并对波纹管采取人为的薄壁磨损破坏,磨损厚度分别为0、0.4、0.8、1.2 mm。每次磨损后采用相同采集方法收集30组数据,每组包含10万条振动数据,将最终得到的多组测试数据导入已经训练好的HMM 模型进行故障检测。通过大量振动数据的反复测试,测试结果见表6。表6中,数据1 是波纹管正常工作时的数据,可见GMMHMM 诊断正常信号的识别率为96.7%,数据2、数据3及数据4均为波纹管有磨损时的故障数据,其故障识别率高达96.7%,可判断为故障,故该HMM 模型可以对工作中波纹管的运行状态进行有效判断。

表6 测试数据结果
此算法实现了对波纹管工作状态的精准识别,解决了之前波纹管遇到的问题。为了方便监测波纹管,在后期需要设计用户管理界面,及时将数据通过发射模块发送到接收模块,实现对波纹管的实时监管。
5 结束语
波纹补偿器用于补偿因各种环境因素尤其是户外振动导致的管道损害。为避免降低生产效益及威胁生产安全问题,对波纹管的振动信号分析尤为重要。利用传统的算法分析时,傅里叶分析及快速傅里叶分析都存在识别精度不高的问题。为此,本文提出了一种基于GMM 训练与HMM 变换的波纹管振动信号分析算法,实现了对波纹管故障的精确诊断。通过多次实验,故障识别率高达96.7%,能有效判别波纹管故障情况,实现了对波纹补偿器运行状态的准确识别。此算法为振动信号诊断领域提供了理论依据。
