地铁列车运行诱发地面邻近建筑振动的数值模拟研究

路德春 高泽军 孔凡超 马一丁 沈晨鹏 杜修力

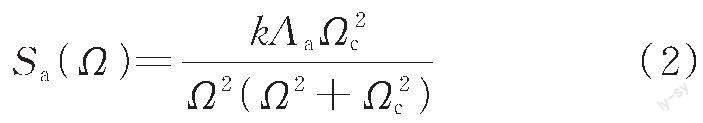
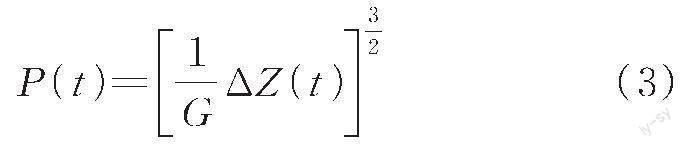
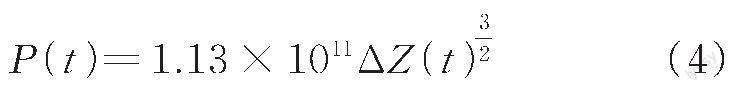
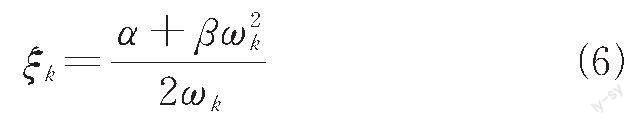
摘要：为研究城市地铁运行产生的振动波在地面邻近建筑物中的传播规律，以地铁沿线邻近建筑为研究对象，参数取值参考实际工程量值范围，建立地铁列车-轨道-隧道-地层-建筑物整体有限元数值模型，重点研究地面邻近建筑中同楼层和不同楼层间振动响应的传递分布规律和频谱特性。结果表明：地铁运行对建筑的振动激励以中低频1～50 Hz为主；房间面积越大，楼板自振频率位于激励荷载优势频段范围越多，越易引起楼板共振；楼板跨中点的振动强度通常大于边角点的振动强度，角点的振动会在低频段1.25～2.0 Hz超过楼板跨中点；随着楼层的升高，三向振动加速度响应均呈波动性变化。通过多工况的计算，分析了运行车速、隧道埋深和振中距对邻近地铁建筑物振动响应的影响规律。

关键词：地铁振动；邻近建筑；整体分析法；数值模拟；振动分布

中图分类号：TU312；U211.3     文献标志码：A     文章编号：2096-6717（2023）06-0113-12

Numerical study on vibration of ground building adjacent to metro induced by operation of subway train

LU Dechun1， GAO Zejun1， KONG Fanchao1， MA Yiding1， SHEN Chenpeng2，DU Xiuli1

（1. Institute of Geotechnical and Underground Engineering， Beijing University of Technology， Beijing 100124， P. R. China； 2. Beijing Urban Construction Design & Development Group Co.， Ltd， Beijing 100034， P. R. China）

Abstract： In order to study the propagation pattern of vibration wave generated by urban subway operation in buildings adjacent to the metro and provide guidance for engineering practice， this paper takes adjacent buildings along the subway line as the research object and refer to the range of actual quantities to establish the general finite element numerical model of subway train-rail-tunnel-ground-building system. The transmission distribution and spectral characteristics of vibration response of the same floor and different floors in the building are studied. The results show that the vibration excitation of the building caused by subway operation is mainly in the range of 1～50 Hz; The greater the room area， the more the natural vibration frequencies of the floor are located in the dominant frequency range of the excitation load， and the more prone it is to cause floor resonance; The vibration intensity of floor span midpoint is usually greater than that of corner point， and the vibration of corner point will exceed floor span midpoint in low frequency band of 1.25～2.0 Hz; The vibration acceleration response in three directions presents a fluctuating distribution trend with the rise of the floor. Through the calculation of several examples， the influential characteristics of running speed， tunnel burial depth and horizontal distance between building and tunnel are analyzed.

Keywords： subway vibration； neighboring buildings； overall analysis method； numerical simulation； vibration distribution

近年來，随着城市人口增长，交通压力逐年增加，轨道交通作为缓解地面交通压力最有效的方式，得到迅猛发展。地铁在带来出行便利的同时，其运行产生的振动和噪音严重干扰了沿线建筑物中居民的正常生活和精密仪器的正常使用，建筑结构本身也会在长期振动中出现裂缝等破坏[1-4]，引起社会各界的广泛关注，开展地铁环境振动问题的研究具有重要意义。

针对地铁列车运行诱发地面建筑振动的研究，学者们采用的研究方法主要包括现场实测法和数值模拟法。现场实测法[5-8]是利用传感器采集地铁运行引起的建筑振动数据，分析振动规律，该方法虽能获得建筑振动的原始数据，但测量仪器易受到地面交通的影响，且可重复性低、测点数量有限。随着计算机技术的发展，数值模拟方法可考虑轨道-列车的精细化建模、复杂的隧道几何尺寸以及隧道-地层的复杂接触关系，是研究轨道交通引起环境振动问题的适用性方法。常见的环境振动数值模拟方法包括子结构法和整体分析法。子结构法是将地铁振动波的传播路径拆分为若干子结构，以事先获得的荷载激励分析子结构的动力响应。Lopes等[9]基于子结构法，提出了预测地下轨道交通引起建筑振动的数值方法，并对振源处的振动控制进行了研究。部分学者利用现场实测数据与数值模拟方法相结合开展地铁环境振动影响研究[10-11]，夏倩等[12]、凌育洪等[13]建立了地面建筑模型，将实测地面振动加速度作为荷载输入到建筑底部，分析建筑振动传播规律。子结构法将振源与受振体分离，无法考虑车辆和轨道结构的共同作用对振动特性的影响，且子结构间的动力相互耦合作用难以合理考虑，与实际情况存在一定差别。整体分析法考虑振动波传播衰减全过程和子结构间的动力耦合，建立整体分析模型研究受振体的振动规律，可合理弥补子结构方法缺陷。Yang等[14]通过解析方法获得地铁列车荷载，作为数值模型的外部激励，对地面大型建筑物在不同地铁列车运行条件下产生的振动进行了研究。马晓磊等[15]对高速地铁运行产生的建筑振动问题开展了数值研究，对比分析不同基础形式下建筑的振动响应规律。杨觅[16]建立三维整体有限元模型，研究了西安地裂缝场地条件下地铁运行引起的建筑物动力响应。在数值研究中，学者们对列车荷载和建筑结构进行大量简化，缺少精细化的建模会造成受振体动力响应与实际情况存在较大差距。此外，现有研究的关注内容大多为振动波在建筑中不同楼层间的传播规律，较少研究同一楼层中不同位置的房间以及同一房间不同位置的动力响应差异性研究。

笔者利用有限元软件ABAQUS，以邻近地铁线路的地面建筑为研究对象，参数取值参考实际工程量值范围，引入无限元边界，耦合各振动子结构，建立地铁列车-轨道-隧道-地层-建筑物精细化三维整体有限元数值模型，研究地铁列车振动荷载作用下地面建筑中同楼层的振动分布规律及不同楼层间的振动传播规律，并开展影响参数分析，获取振动响应特征。

1 地铁环境振动数值模型

地铁列车运行时，轮轨相互作用是地铁振动产生的源头。车轮与钢轨撞击产生的振动经由支撑块、道床、隧道衬砌及地层向地表传播，进而诱发地面建筑的振动响应。

1.1 列车-轨道系统

列车系统和轨道系统的建立，分别考虑列车各部件不同的自由度特征和钢轨轨面的不平顺，通过Hertz接触模型确定轮对和轨道之间的垂向作用力，水平作用力采用罚接触。

1.1.1 列车系统

根据实际地铁列车结构建立列车数值模型。模型包括车体、转向架、轮对，以及一系、二系悬挂结构。采用不同的自由度设置实现列车各部件不同的运动特征：车体和转向架考虑横移、沉浮、点头、摇头和侧滚5个自由度，轮对考虑横移、沉浮、摇头和侧滚4个自由度，列车模型共计31个自由度，可全面反映地铁列车行进过程中的动力行为。列车物理模型如图1所示。

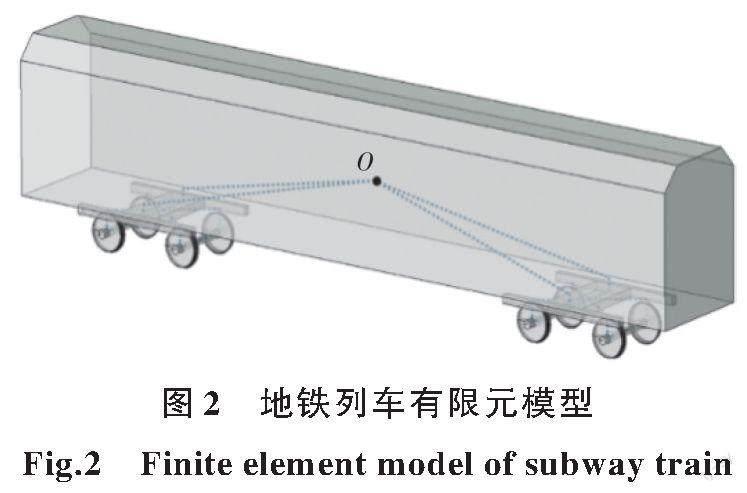
地铁列车模型中，假定车体、转向架及轮对为刚体，忽略部件的弹性变形。模型采用离散刚体建立车体和转向架部件，采用解析刚体建立车轮部件，选用磨耗型车轮踏面。轮对与转向架间通过一系悬挂连接，车体与转向架间通过二系悬挂连接。地铁列车有限元模型如图2所示，文中列车位置的描述以车体的质心O为基准。

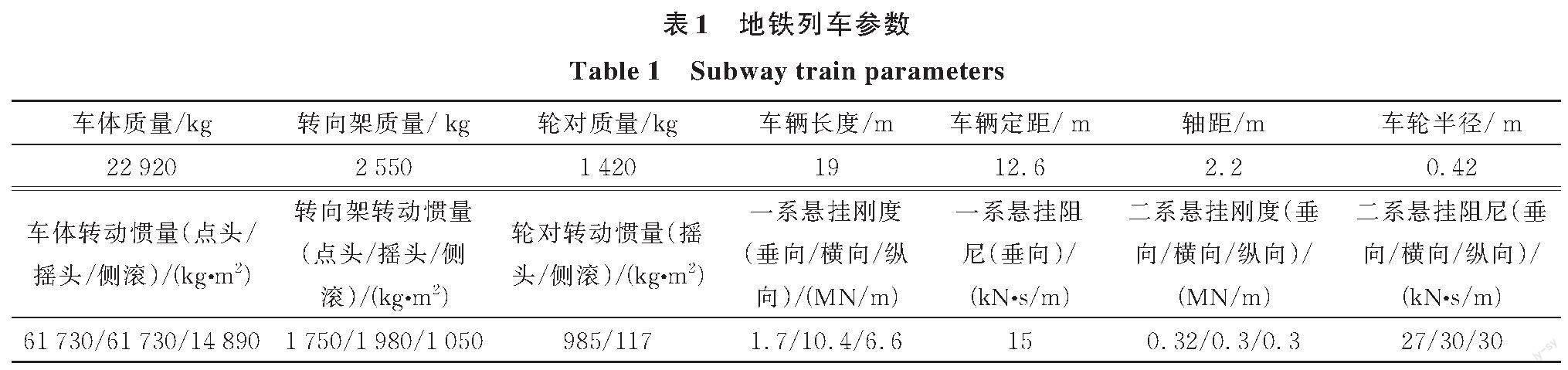
列车的几何参数、惯性特征和悬挂参数是影响仿真效果的关键因素。建模時通过在列车部件质点处设置质量和转动惯量来考虑列车结构的空间自由度，一系、二系悬挂的空间刚度与阻尼采用三向Cartesian连接器。地铁列车模型参考北京地铁B型车参数进行设置，如表1所示。

1.1.2 轨道系统

参考实际地铁隧道，轨道系统采用混凝土支承块式整体道床，支承块铺设标准为1 600根/km。钢轨模型横断面尺寸参考60 kg/m钢轨，轨道上采用DTⅥ2型扣件，扣件刚度为60 MN/m，阻尼系数为50 kN⋅s/m，通过Cartesian连接器来实现扣件的模拟。

轨道不平顺指实际轨道垂向和横向轮廓相对理想位置的几何偏差，是列车-轨道耦合系统动力相互作用的主要激励源，对轮轨的动力响应以及列车运行安全性与舒适性有显著的影响[17-18]。因此，轨道不平顺的合理模拟是地铁环境振动研究的重要环节。

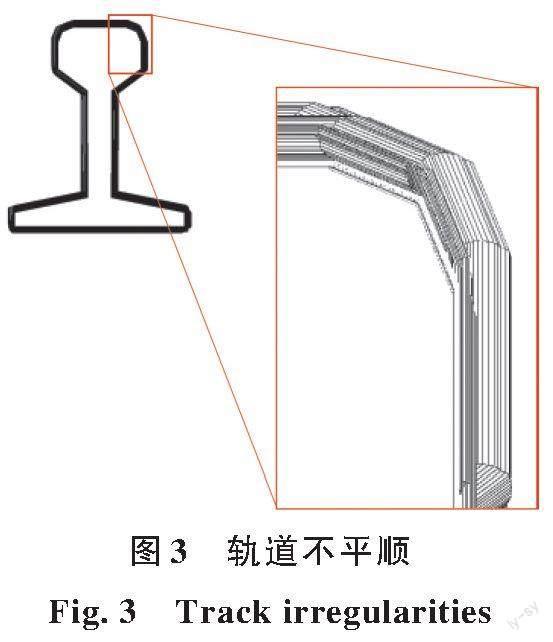
模型采用美国铁路管理局根据大量实测资料得到的轨道6级不平顺谱密度函数，计算出钢轨高低不平顺序列和方向不平顺序列，将不平顺序列值施加到钢轨有限元模型网格结点，实现轨道不平顺的模拟。模型中的轨道不平顺如图3所示。高低不平顺谱和方向不平顺谱的表达式为：

高低不平顺

方向不平顺

式中：S （ Ω ）为轨道不平顺功率谱密度，cm2/（rad/m）；Ω 为轨道不平顺的空间频率，rad/m；Av、Aa 是粗糙度常数，cm2/（rad/m）；Ωc 是截断频率，rad/m；k 是安全系数，一般取为0. 25。

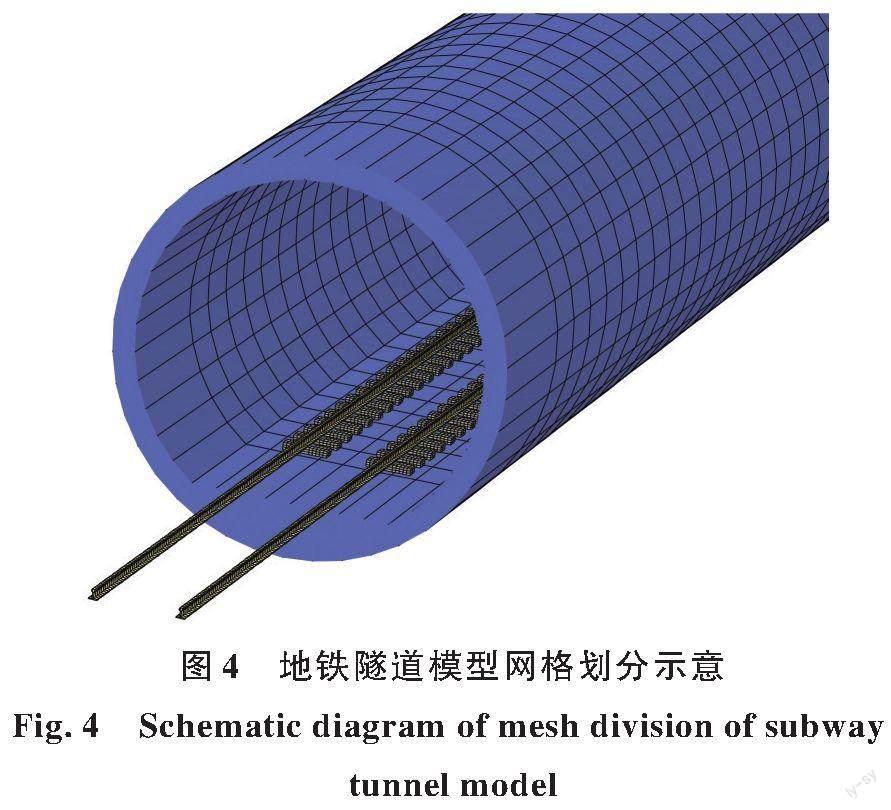
粗糙度常数Av=Aa=0. 033 9 cm2/（rad/m），截断频率Ωc=0. 824 5 rad/s[19]。钢轨沿列车行驶纵向方向的网格尺寸为0. 1 m，横断面网格尺寸最小为0. 012 m，最大为0. 095 m；轨道不平顺空间取样步长设置为0. 005 m，小于钢轨纵向网格尺寸，满足钢轨模型结点不平顺插值的精度要求。地铁隧道模型网格分布示意如图4 所示。

1.1.3 轮轨接触关系

轮对和轨道之间的接触是影响地铁振动模拟结果的关键因素，轮轨接触关系的正确描述直接影响模型分析的准确性[20]。模型采用罚接触模拟轮轨间切向摩擦作用，摩擦系数取为0.3；轮对与钢轨法向接触产生的轮轨作用力通过Hertz非线性弹性接触模型确定，根据该理论可计算得到轮轨接触法向力

式中：G 为轮轨接触常数，m/N2/3；对于磨耗型踏面车轮，G 取3. 86R-0. 115×10-8，对于锥形踏面车轮，G取4. 57R-0. 149×10-8（R 为车轮半径）。ΔZ （ t ） 为t 时刻轮轨间的弹性压缩量，m。列车模型的车轮半径R=0. 42 m，车轮踏面为磨耗型，由式（3）计算可得

由式（4）可得轮对与轨道间不同弹性压缩量下的接触法向力变化曲线，曲线上取若干离散点，输入软件相互作用模块，以实现轮轨Hertz接触设置。

1.2 地面建筑结构

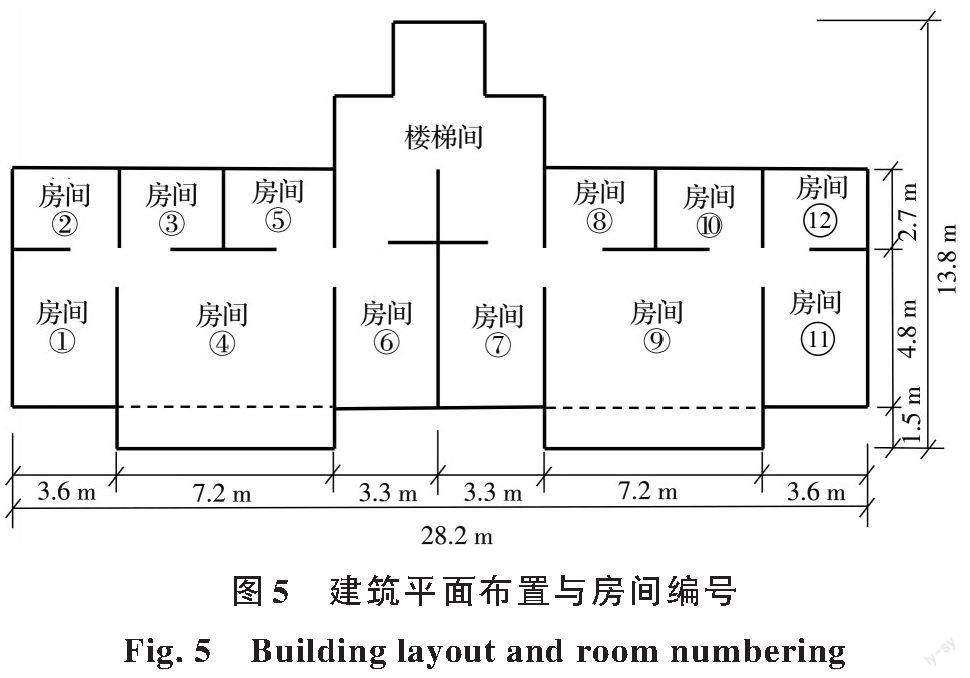
以地铁线路的地面邻近建筑作为研究对象，该建筑为框架-剪力墙结构，地上部分11层，层高3 m；地下部分1层，层高2.7 m。建筑平面每层面积为253.98 m2，共12个房间，建筑物平面布置与房间编号如图5所示。建筑模型采用箱形基础，建筑平面长轴与隧道Z向中心线平行，位于隧道行驶方向右侧位置，建筑平面形心与既有地铁线路中心线水平距离为11 m，隧道拱顶埋深15 m，隧道与建筑的空间位置关系如图6所示。地铁盾构隧道直径以6～7 m范围居多，以7 m盾构隧道为例开展地铁环境振动研究，衬砌厚度为0.4 m。

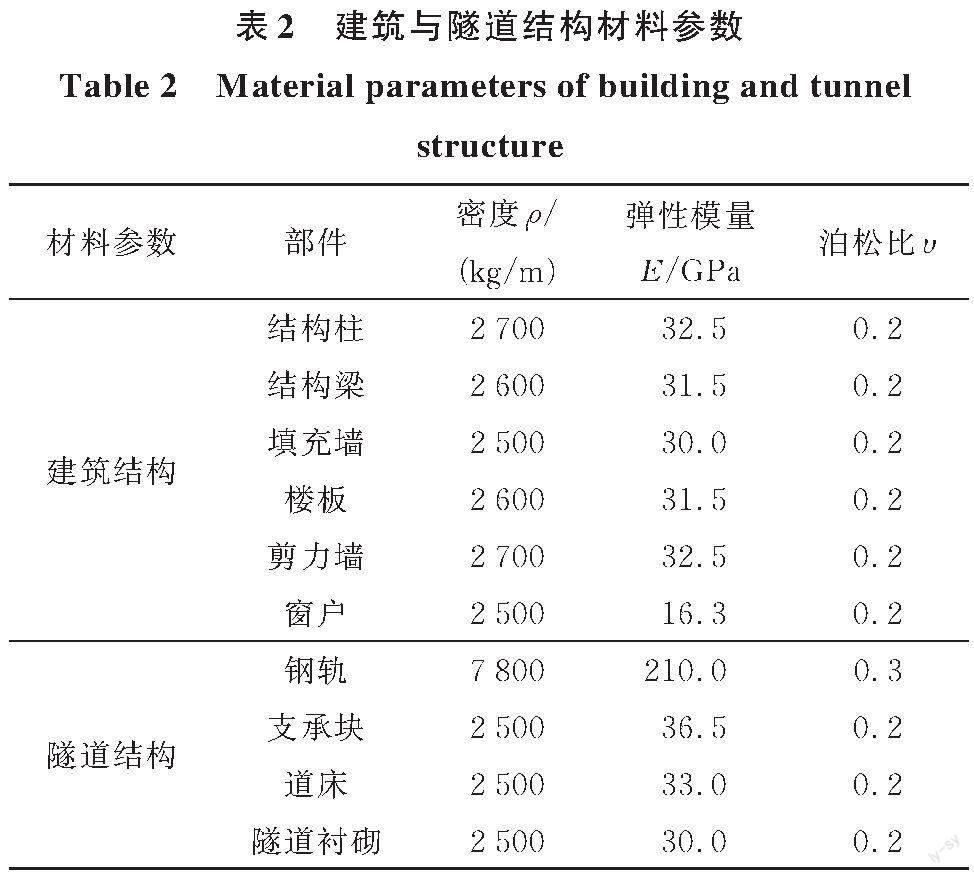
建筑地下室部分与周围土体表面在地铁列车振动荷载作用下变形较小，可视为协同变形，不发生相对分离，故在模拟时将二者的接触面设定为绑定接触。建筑模型中的楼板、剪力墙、填充墙和窗户部件均为S4R壳单元，厚度分别为0.12、0.2、0.2、0.05 m；结构梁和结构柱采用B31梁单元，梁截面尺寸为0.2 m×0.3 m，柱截面尺寸为0.5 m×0.5 m。建筑结构部件材料参数如表2所示。

建筑模型中各部件之间的连接在ABAQUS软件中通过网格节点合并的方式实现。建筑标准楼层有限元模型如图7所示，建筑地上部分有限元模型如图8所示，模型中不同颜色的部分代表不同的建筑部件。

1.3 边界条件与材料参数

模型采用由Lysmer等[21]提出的无限元边界，消除地铁振动波在地层边界的反射影响，无限元边界通过在模型边界上引入阻尼力吸收振动波的辐射能量，模拟能量向无穷远处传播，避免了波在人工截断边界的反射，适用于地铁环境振动的域内局部振动问题。在ABAQUS软件中，通过将模型的边界单元属性设置为无限单元CIN3D8得到无限元边界。地层模型的地面设置为自由边界，模型底部及四周均设置为无限元边界。

土是一种颗粒型摩擦材料，存在剪切变形机制，在地铁列车行駛时产生的振动荷载作用下，土体会产生一定的塑性累积变形，模型采用Mohr-Coulomb 弹塑性本构模型反映土体上述特点，其中密度ρ=2 030 kg/m3，弹性模量E=400 MPa，泊松比v=0. 32，摩擦角φ=26°，黏聚力c=18 kPa。引入Rayleigh 阻尼来反映振动在土层材料中的能量耗散，其阻尼矩阵表达式为

C = αM + βK （5）

式中：C 为阻尼矩阵；M、K 分别为质量矩阵和刚度矩阵；α 和β 分别为与质量和刚度相关的阻尼系数。

Rayleigh 阻尼属于正交阻尼，可用正交条件确定阻尼系数。阻尼系数α 和β 与各阶振型阻尼比ξk之间的关系为

式中：ωk 为第k 阶振型的固有圆频率，k=1，2，3…n，n 为总振型数。

选取关心频段（5～80 Hz）的端点值作为体系固有频率，阻尼比根据相关文献取为0. 03[22]，确定阻尼系数为α=1. 77 s-1，β=1. 12×10-4 s。

盾构管片通常为C50混凝土[23]，弹性模量为34.5 GPa，综合考虑盾构隧道纵向和环向接头对衬砌整体刚度的影响，对隧道衬砌的弹性模量进行了折减，取为30 GPa。实际工程中支撑块、道床和盾构管片紧密连接，将模型中支撑块和道床间、道床和隧道衬砌间设置为绑定接触。隧道结构各部件材料参数见表2。由于地铁列车通过时隧道结构各组成部件均处于弹性变形阶段，故模型中钢轨、支承块、道床和隧道衬砌均采用线弹性本构模型。地层土体和隧道结构的有限元部分采用八节点六面体实体单元C3D8R模拟。

1.4 整体地铁环境振动数值模型

ABAQUS软件中的Explicit模块可以有效进行各类非线性分析，适合用于计算复杂系统多场耦合的地铁环境振动问题。

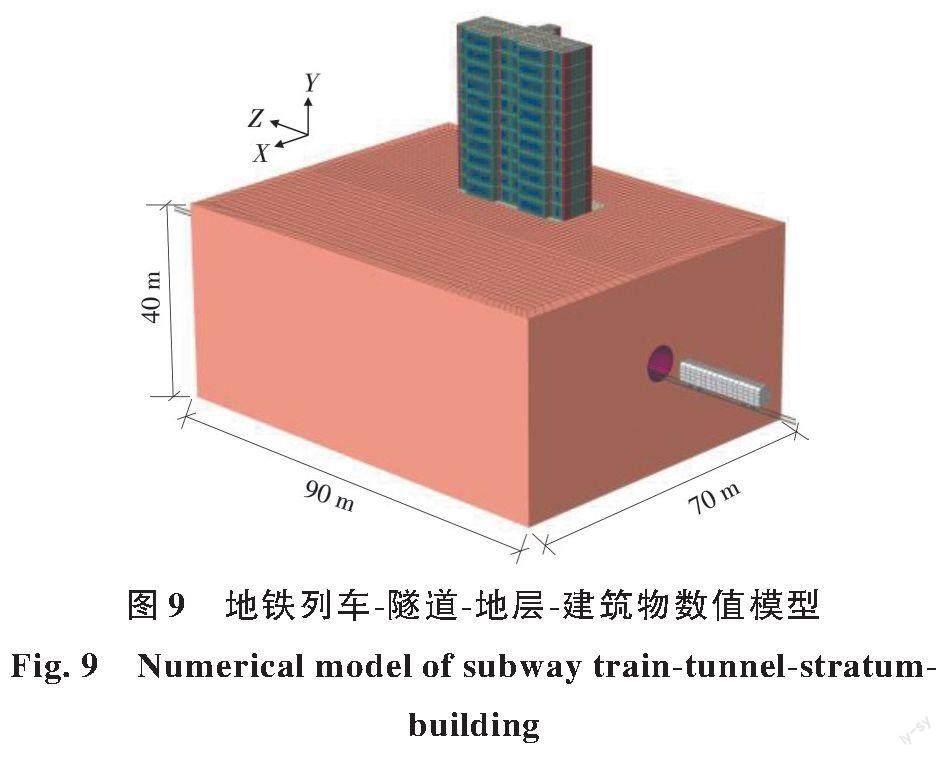
综合考虑模型的计算精度和计算效率，土体尺寸取为纵长90 m、宽度70 m、深度40 m，模型共划分为约25万个单元。为避免列车起步时全速运行对隧道产生强烈冲击而导致的振动数据失真，对轨道进行外延，列车运行起始位置在土体前方15.5 m。研究对象为地面建筑的振动响应，故将实际地铁列车编组简化为单节列车车厢，模型中的列车行驶速度设置为80 km/h。求解时间步长为0.000 5 s，即采样频率为2 000 Hz，由采样定理[24]在实际应用中将采样频率设置为信号最高频率的2.56～4.00倍可知，步长设置可有效计算500 Hz以内的振动，满足研究所关注的频率范围。建立地铁列车-轨道-隧道-地层-建筑物三维整体有限元数值模型，如图9所示。

1.5 模型验证

针对实际工程中的地铁列车运行引起一栋6层扩大基础建筑物的振动问题[25]，采用文献[25]中的几何尺寸及材料参数，采用本文的有限元模型建模方法和地铁列车-轨道系统模型，建立地铁环境振动三维有限元模型，验证地铁环境振动模型建模方法的合理性。验证模型的建筑物与文献[25]中建筑物E相同。

对比地铁列车通过时建筑第1层、第3层和第6层竖向振动的1/3倍频程分频加速度级，如图10所示。结果显示，数值模拟结果与现场测量数据之间吻合较好，分频加速度级变化趋势一致，表明提出的地铁列车-轨道-隧道-地层-建筑物三维数值模型建模方法的合理性。

2 建筑振动响应分布和传播规律分析

2.1 建筑激励荷载特性分析

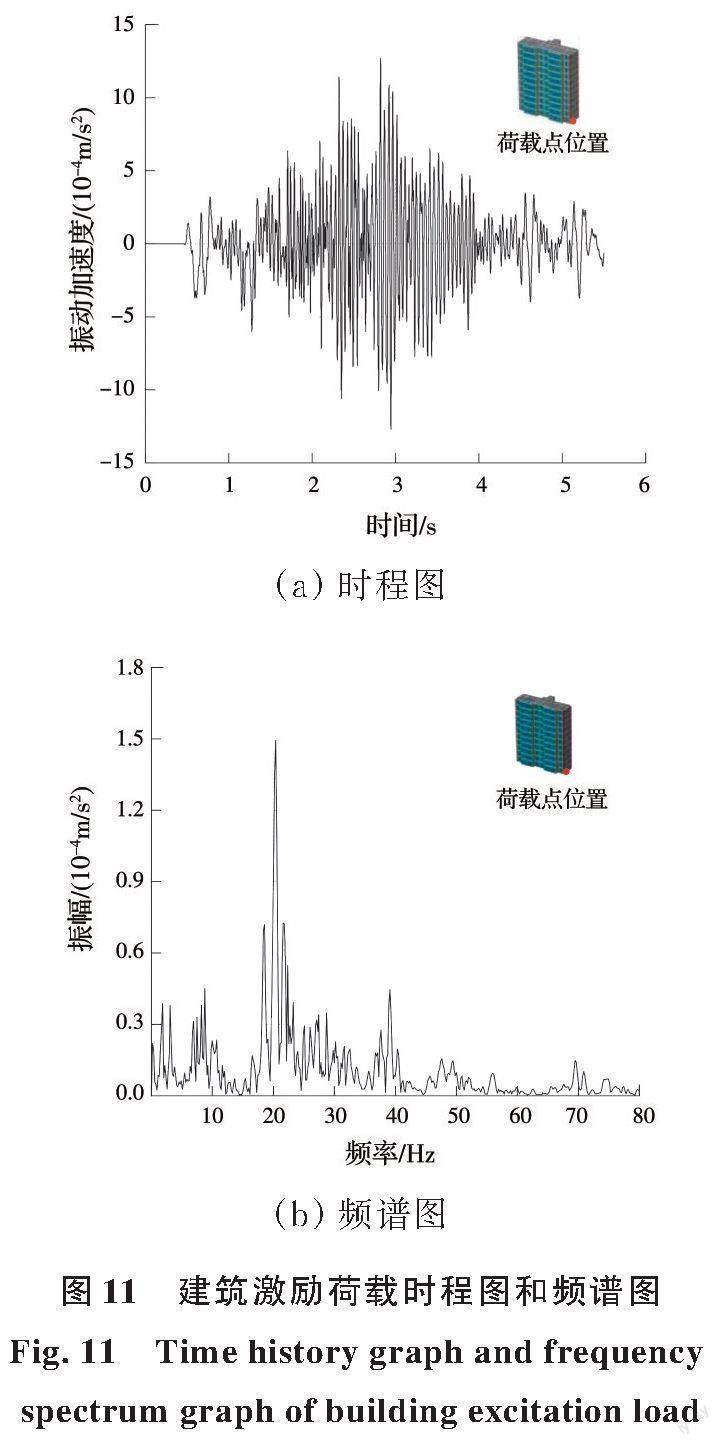
选取模型中地面建筑与地层某处分界点的竖向加速度响应作为建筑的激励荷载进行分析，得到其时程图和频谱图，如图11所示。由图11可得知，激励荷载的竖向加速度峰值为0.001 27 m/s2，振动响应随着列车的驶近逐渐提高，随着列车的驶离又逐渐减小，加速度时域波形外轮廓呈现出“梭形”。振动波经过地层传递至地表后，其高频部分能量衰减较大，对建筑物的振动激励以中低频为主，优势频段处于1～50 Hz之间，主频位于20 Hz附近。

2.2 建筑同楼层房间振动响应分布规律

地铁运行诱发建筑同楼层房间振动响应分布规律的分析，包括同楼层不同房间的振动分布、同一房间不同位置的振动差异。对拾振点的竖向振动开展研究。

2.2.1 建筑同楼层不同房间的振动响应分布

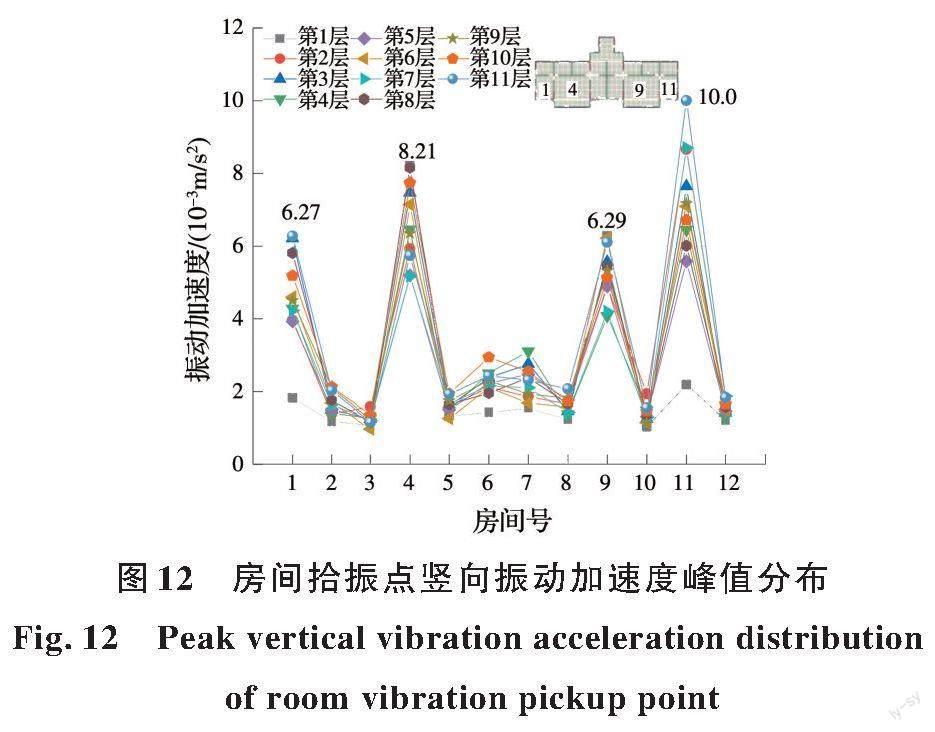
提取建筑中所有房间共132个拾振点的振动时程，得到建筑不同楼层的房间拾振点竖向加速度峰值分布，拾振点位于房间楼板的跨中点处。从图12可以看出，在地铁列车通过时，同一楼层中振动加速度峰值在1、4、9、11号房间存在极值，其中，4号和9号房间是地面建筑中面积最大的两个房间，1号和11号房间面积次之。1、4、9、11号房间在楼层中达到的振动峰值最大值分别达到0.006 27、0.008 21、0.006 29、0.010 m/s2，房间振动响应在不同楼层间有所差别，但总体规律相近。

选取建筑首层的1、4、9、11号房间的竖向振动数据，根据行业标准《城市轨道交通引起建筑物振动与二次辐射噪声限值及其测量方法标准》（JGJ/T 170—2009），转换为1/3倍频程中心频率上的最大振动加速度级作为振动评价量，分别为67.6、83.0、78.6、67.4 dB，均超过标准中对居民区建筑要求的振动限值（昼间不超过65 dB，夜间不超过62 dB），将会对建筑中的人体舒适度产生不良影响。

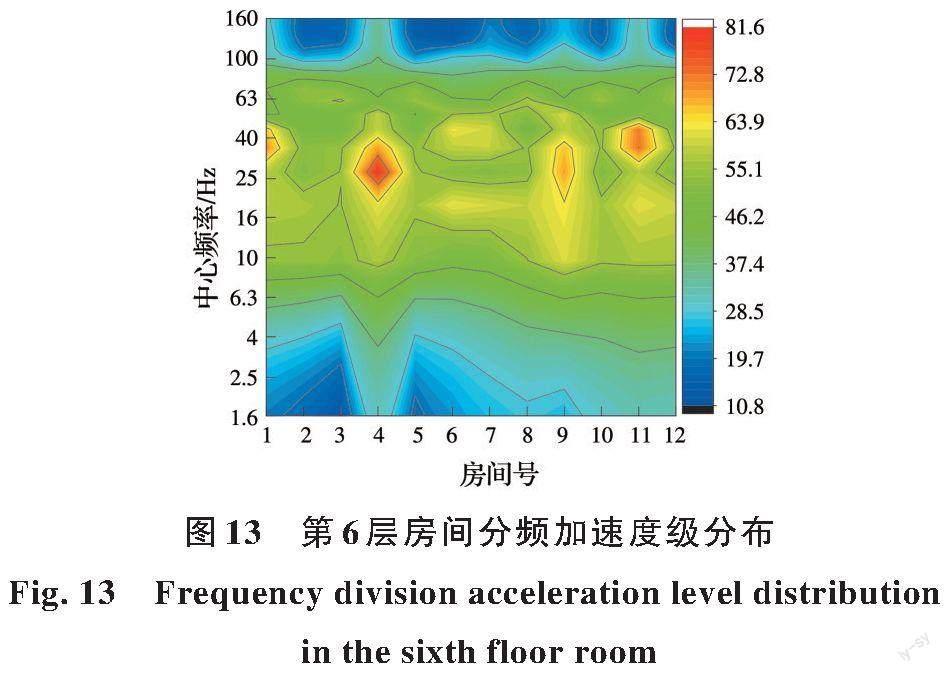
为直观表明建筑同一楼层内不同房间拾振点频域内的振动响应规律，以第6层为例，计算了12个房间拾振点的1/3倍频程分频加速度级，并绘制云图，如图13所示，其余楼层拾振点的分频加速度级具有类似的分布规律。由图13可见，房间振动响应主要集中在16～50 Hz范围内，其中，4号和9号房间振动在25 Hz左右振动显著；1号和11号房间振动在40 Hz左右振动显著。

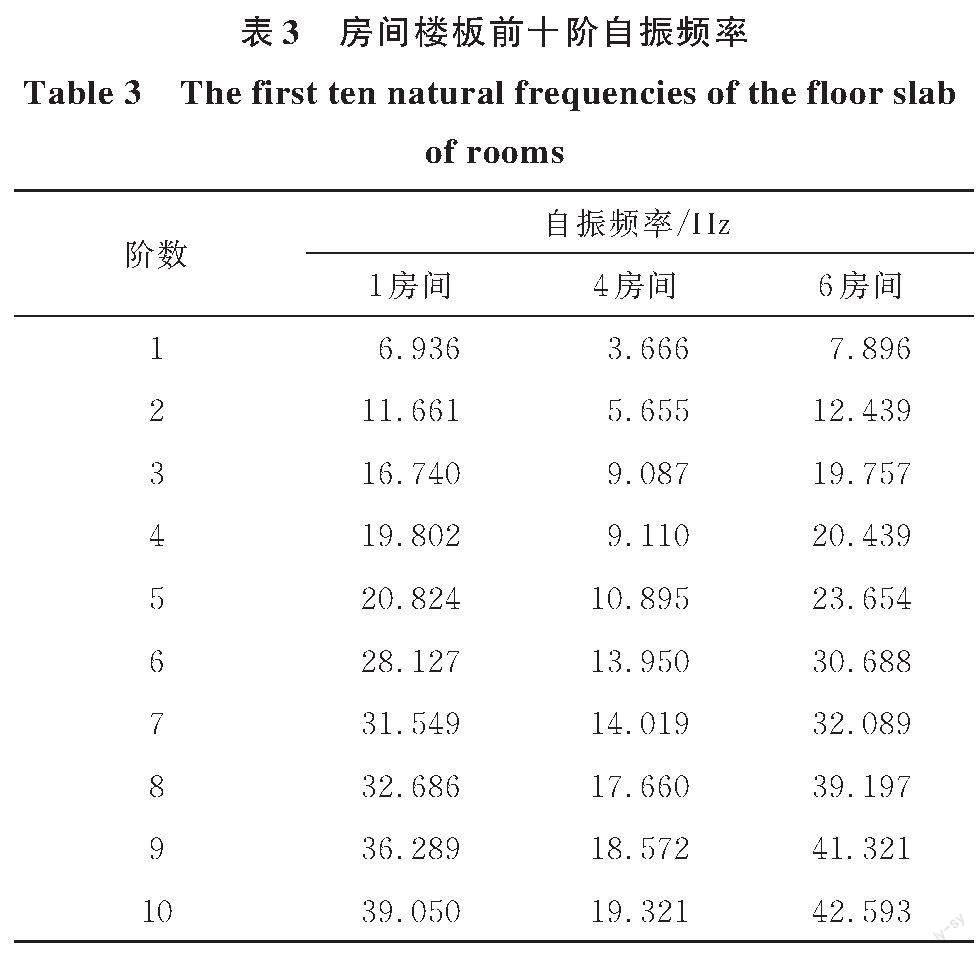
对1号（4.8 m×3.6 m）、4号（4.8 m×7.2 m）和6号（4.8 m×3.3 m）3个房间的楼板单独建模得出前10阶自振频率，如表3所示。从表3可以看出，房间楼板面积越大，其自振频率越低，楼板自振频率位于建筑激励荷载优势频段范围越多，越易在特殊频率附近引起楼板共振，导致该房间振动响应较大。此外，对于4号和9号、1号和11号房间，其楼板尺寸及振动显著频率相同，但振动响应大小有所差别，这表明房间所处建筑平面中的位置对地铁引起的振动响应也产生一定的影响。

2.2.2 楼板跨中与边角处振动响应的对比分析

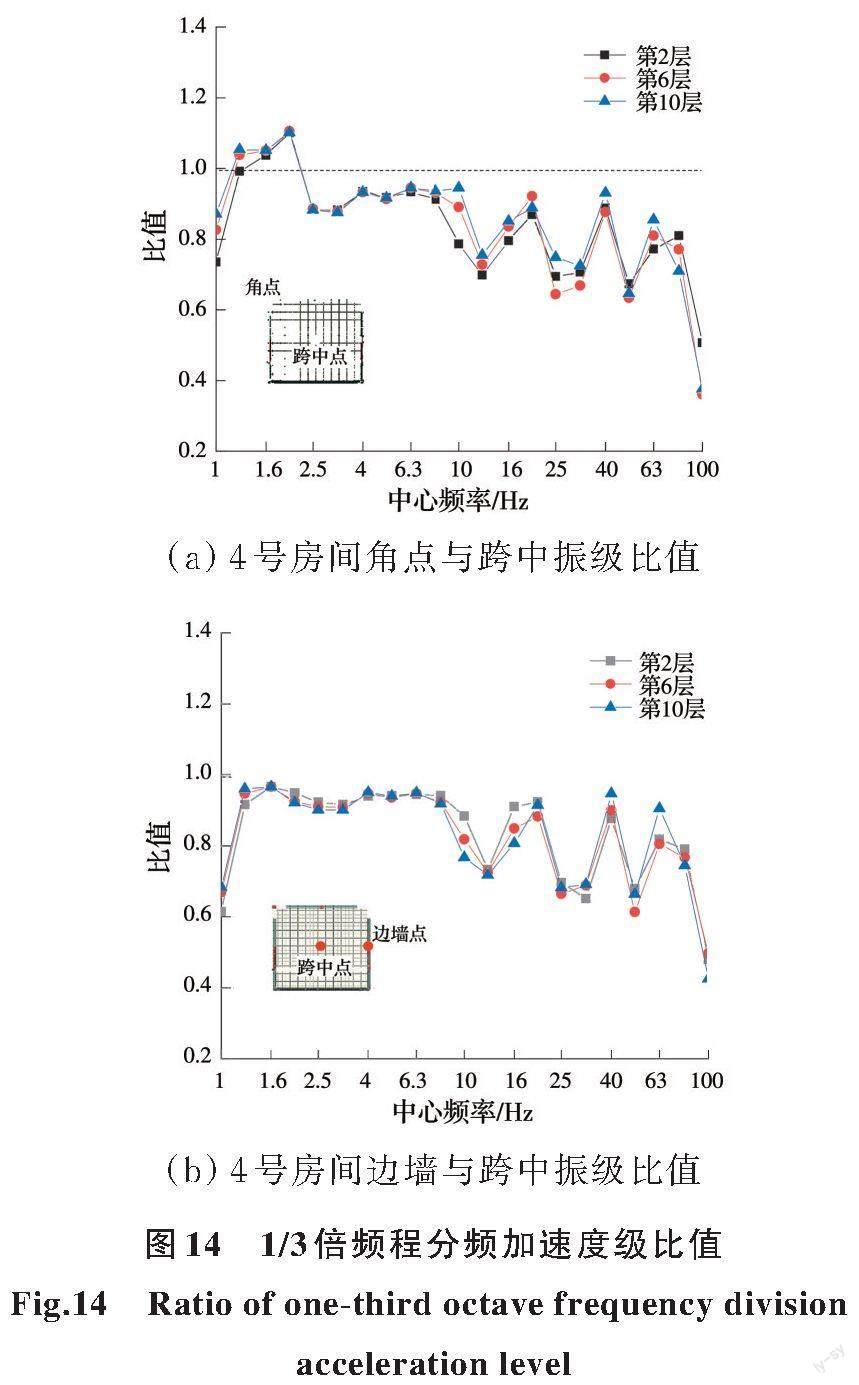
为了分析同一房间楼板跨中点位置与边角位置处振动响应的差别，表4以1号和4号房间的3个楼层为例，给出了楼板跨中点、边墙点（梁中间处）和角点（柱边缘处）竖向振动加速度峰值的对比数据。分析中提到的边角点包括边墙点和角点。从表4中可以看出，跨中点的加速度峰值明显大于边墙点和角点加速度峰值，角点与边墙点的振动强度相近。其原因在于楼板四周向中心位置处传递的振动波叠加，且楼板跨中点的刚度小于周围边角点的刚度，导致楼板跨中点处振动强度较大。

图14所示为4号房间楼板边角点与跨中点在1/3倍频程中心频率处分频加速度级的比值。由图14可知，不同楼层边角点振级与跨中点振级比值随着中心频率变化趋势基本相同；楼板角点与跨中点振级的比值在低频段1.25～2.00 Hz内出现大于1的现象，在其余频段内均小于1；楼板边墙点与跨中点振级的比值在所有频段内均小于1。总体呈现的规律为楼板跨中点的振动强度通常大于边角点的振动强度，在低频段由于局部共振的原因导致角点振动放大，超过同一楼板跨中点的振动强度。

2.3 建筑房间振动响应沿楼层传播规律

为研究振动在不同楼层间的振动传播规律，分析了三向振动加速度峰值随楼层变化分布和1/3倍频程分频加速度级的楼层最大差值分布。以1、4、9、11号房间作为研究对象。

2.3.1 三向振动加速度峰值随楼层变化分布

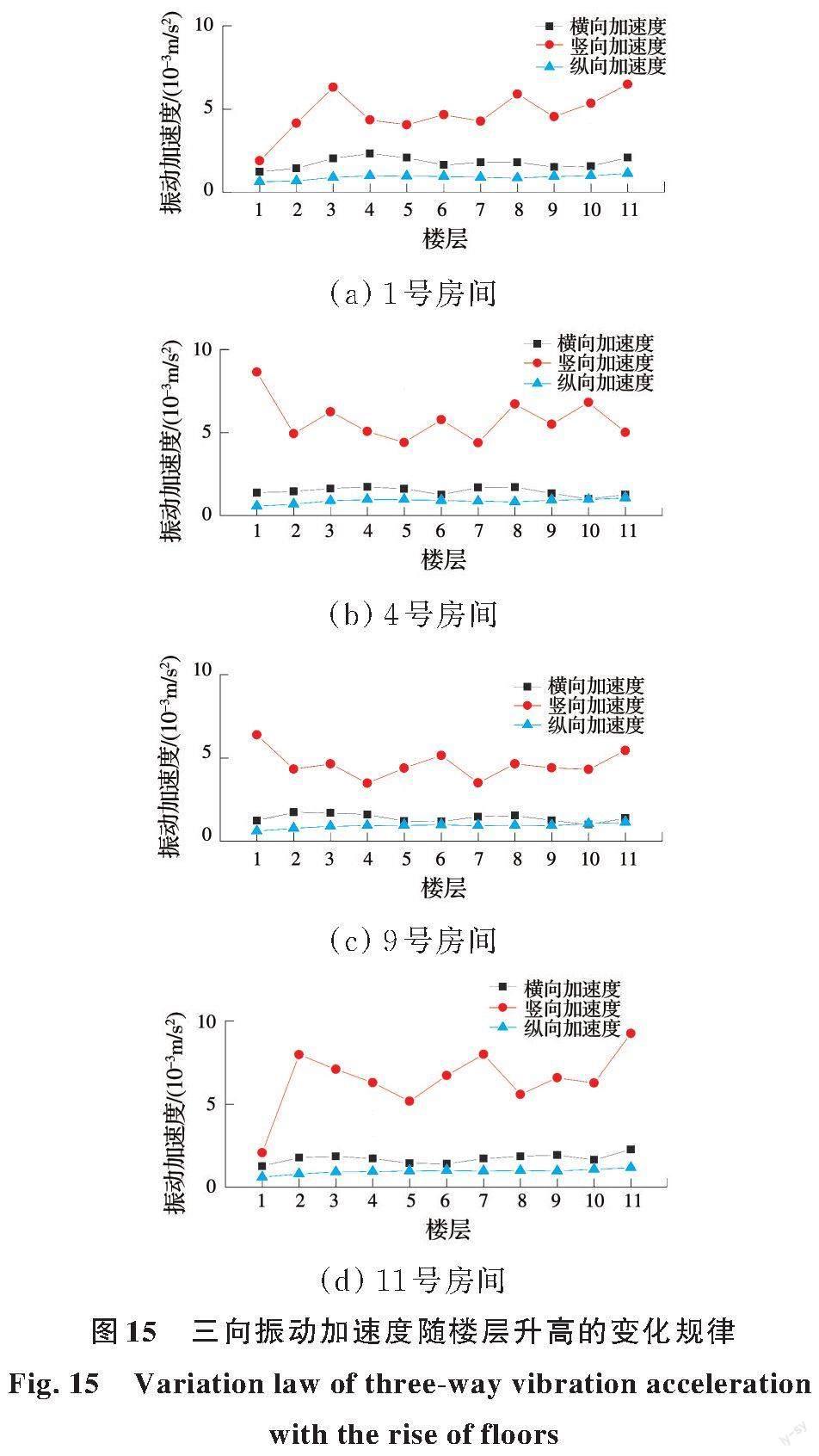
1、4、9、11号房间三向振动加速度峰值随楼层变化分布如图15所示。从图15可以看出，房间的竖向加速度响应随着楼层的升高并非呈现单调变化规律，而是表现出波动变化的趋势。1、4、9、11号房间顶层与底层竖向振动响应数值的比值分别为4.32、0.58、0.85和4.47，即1号和11号房间的振动响应随楼层升高而波动增大，4号和9号房间的振动响应随楼层升高波动减小。

4个房间的横向和纵向加速度响应随楼层的升高同样呈波动变化的趋势，但与竖向加速度相比，总体变化幅度较小。房间各楼层竖向振动均值约为横向振動均值的2.5～4.0倍，约为纵向振动均值的5～7倍，呈现竖向加速度峰值＞横向加速度峰值＞纵向加速度峰值的规律。上述分析表明，建筑的三向振动加速度响应随楼层的升高呈波动性变化的分布趋势，地铁列车运行引起地面邻近建筑的振动以竖向为主，竖向加速度变化幅度最大、均值最高。

2.3.2 楼层分频加速度级的最大差值分布

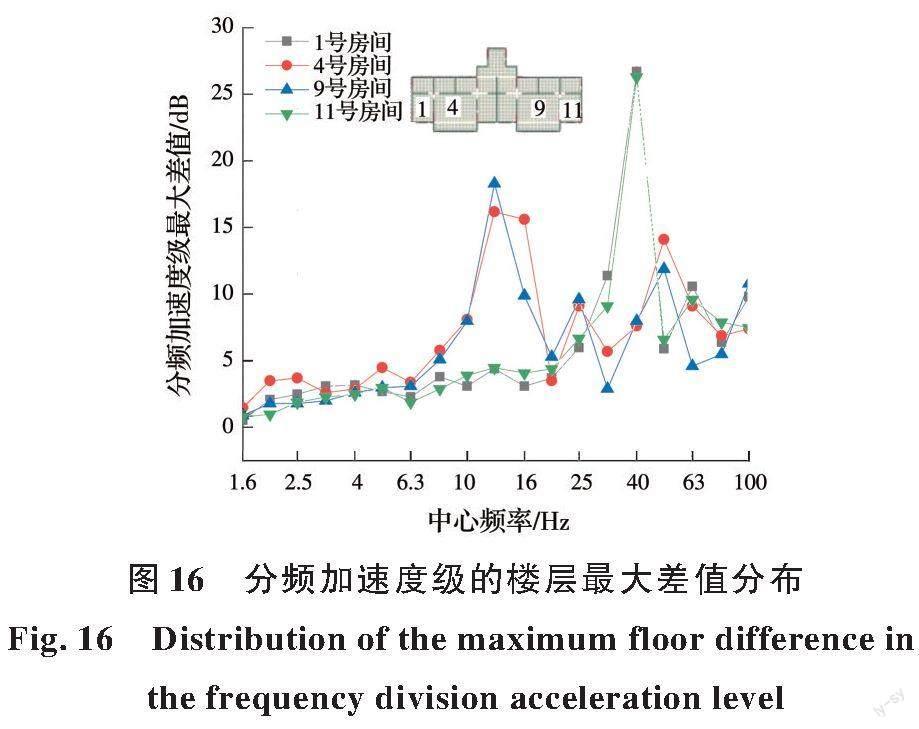
计算出1、4、9、11号房间1/3倍频程中心频率处竖向分频加速度级在所有楼层间的最大差值，分析不同频率的振动在建筑楼层的变化幅度，如图16所示。由图16可得，随着频率的升高，同一房间的分频加速度级楼层最大差值总体呈现逐渐增大的趋势。其中，4号和9号房间的振动响应在中心频率10～16 Hz范围内差异显著；1号和11号房间的振动响应在中心频率40 Hz处差异显著。综合第2.2.1节分析结果可知，楼层振动差异显著频率与房间楼板自振特性有关，房间面积越大，自振频率越低，使得楼层振动差异显著频率越低。

3 地铁环境振动影响因素分析

以建立的数值模型为标准工况，分析了运行车速、地铁隧道和建筑物的间距（包括竖向距离、水平距离）对建筑振动的影响规律。竖向间距为隧道埋深，水平间距为建筑平面形心与既有地铁线路中心线的水平距离（简称振中距）。

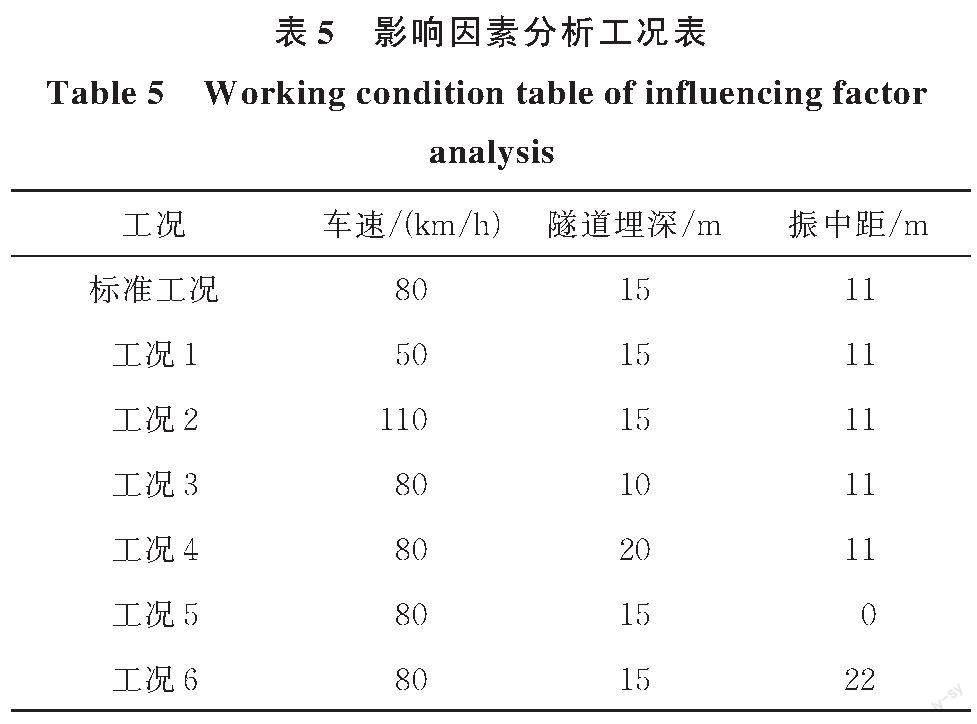
3.1 分析工况

以建筑各楼层的1号房间楼板跨中点作为分析对象，研究拾振点竖向振动加速度峰值在不同工况下的变化规律。对某一因素分析时，其余因素为标准工况下的取值。分析工况如表5所示。

3.2 计算结果分析

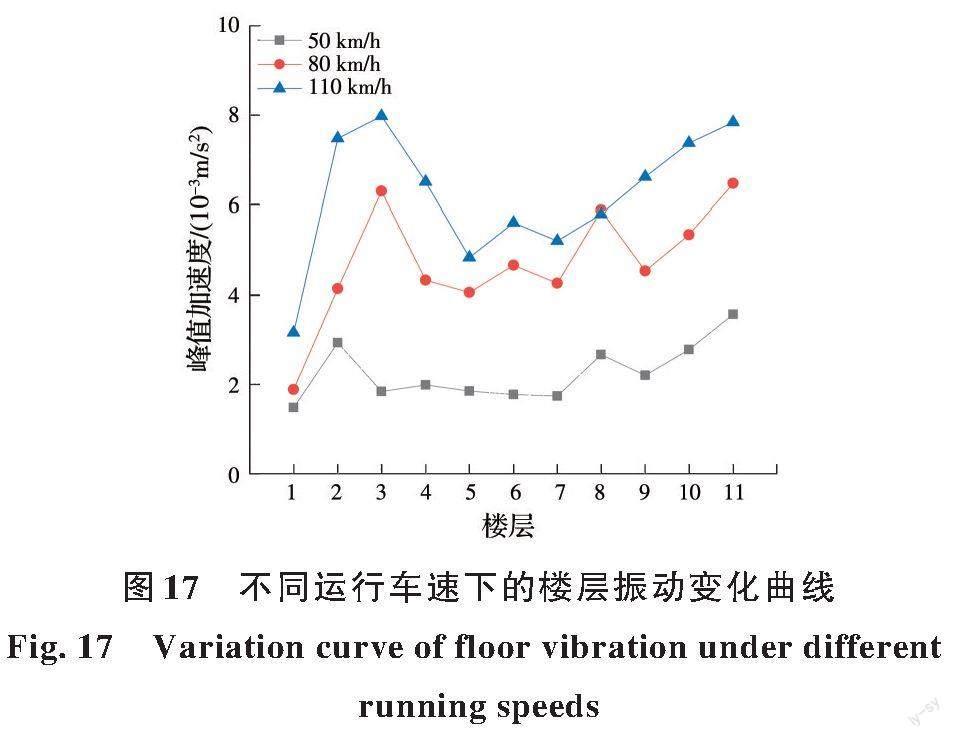
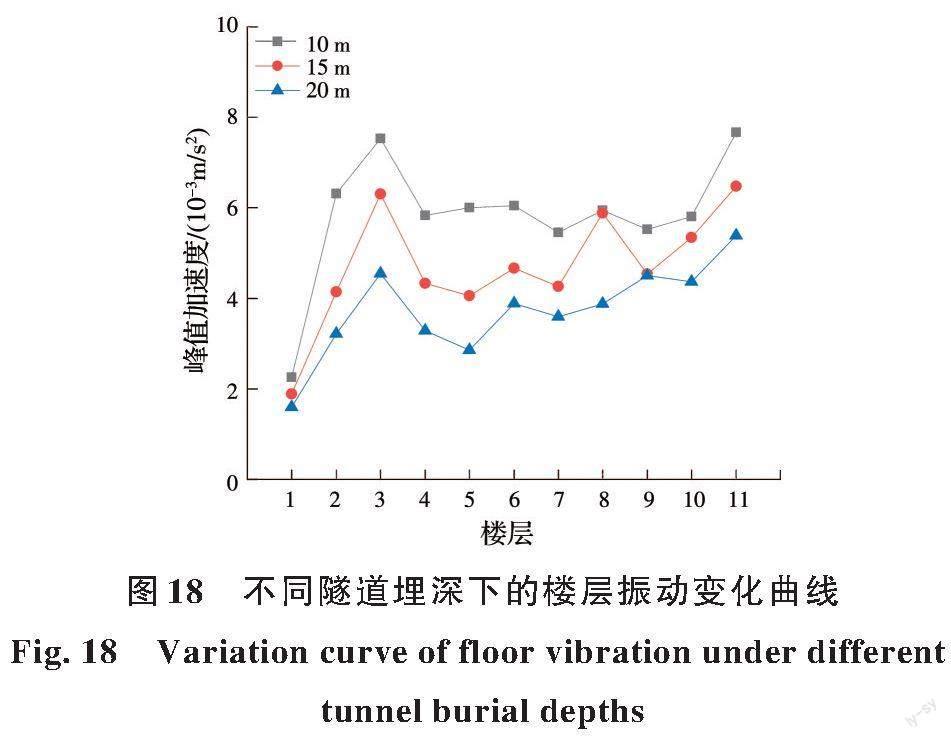
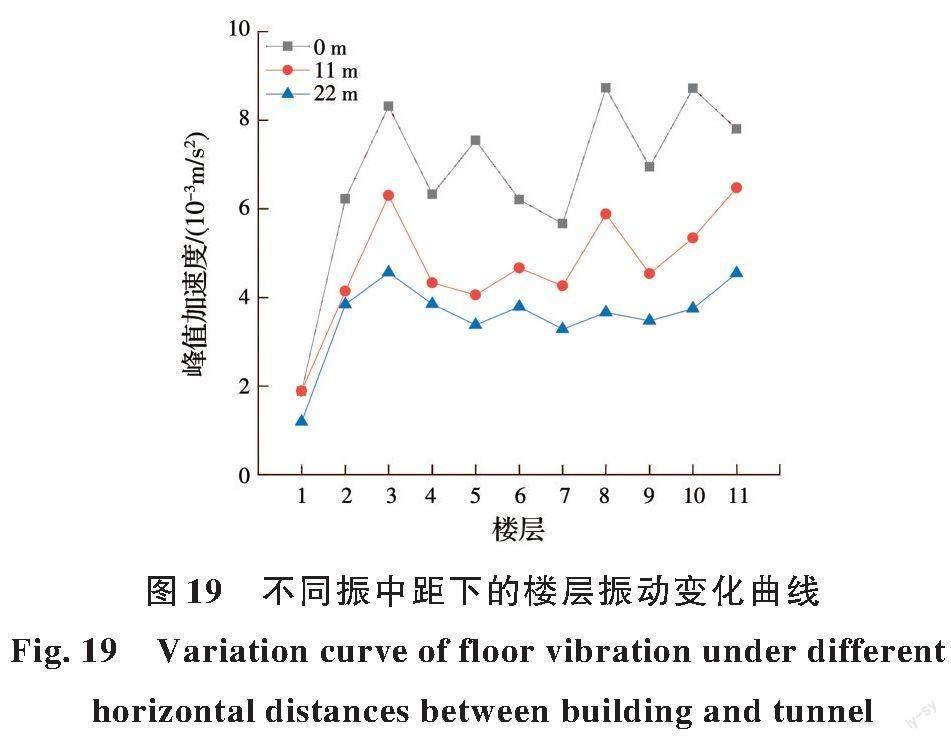
图17～19分别展示了拾振点在不同运行车速、隧道埋深和振中距工况下的竖向振动加速度峰值变化曲线。

由图17可以看出，当隧道埋深和振中距一定时，随着列车运行车速的提高，建筑物振动响应不断增大。当列车运行速度从50 km/h提升到80 km/h时，楼层振动响应均值增加了109.07%；从80 km/h提升到110 km/h时，楼层振动响应均值增加了31.85%。这是由于车速的提高增加了地铁轮轨间冲击力，使得激励荷载大幅提高，建筑振动响应增加。

由图18看出，当运行车速和振中距一定时，随着地铁隧道埋深的增加，建筑物振动响应不断减小。当隧道埋深从10 m增加到15 m时，楼层振动响应均值下降了19.42%，从15 m增加到20 m时，楼层振动响应均值下降了20.87%。地铁运行产生的振动能量经过土层时存在一定程度的衰减，振动传播距离越远，振动能量衰减越多，对建筑振动影响越小。

由图19看出，当运行车速和隧道埋深一定时，随着建筑与地铁隧道的振中距的增加，建筑物振动响应不断减小。当振中距从0 m增加到11 m时，楼层振动响应均值下降了24.24%，从11 m增加到22 m时，楼层振动响应均值下降了24.18%。此外，在建筑物与隧道中心线距离较近时，建筑物振动沿楼层的波动较大；距离较远时，振动响应沿楼层的波动较小。

4 结论

基于有限元软件ABAQUS，建立了地铁列车-轨道-隧道-地层-建筑物数值模型，研究了地面建筑同楼层和不同楼层间地铁列车运行诱发的振动响应规律，并开展影响参数分析，得到如下结论：

1）地铁振动对建筑的激励荷载以中低频为主，优势频段处于1～50 Hz之间；房间面积越大，房间楼板自振频率位于激励荷载优势频段范围越多，越易引起楼板共振，工程中可通过适当缩小房间面积或提高房间楼板自振频率的措施降低地铁振动带来的不良影响。

2）同一房间楼板跨中点的振动强度通常大于边角点的振动强度，角点与边墙点的振动强度相近；局部共振会导致角点在低频段1.25～2.00 Hz的振动放大，超过楼板跨中点的低频振动响应。

3）三向振动加速度随楼层的升高呈波动性变化趋势，其中竖向加速度变化幅度最大；竖向振动均值约为横向振动均值的2.5～4.0倍，约为纵向振动均值的5～7倍，地铁列车运行引起地面邻近建筑的振动以竖向为主；楼层振动差异显著频率与房间楼板自振特性有关。

4）地铁隧道与建筑距离越远，振动衰减越大，对建筑物的振动影响越小；列车运行车速的改变对建筑物振动有较大影响，地铁运营期可优先选择降低敏感区段的车速达到减振目的。

参考文献

[1]  冯青松， 廖春明， 张凌， 等. 地铁振动对人体暴露于全身振动的舒适度影响评价[J]. 噪声与振动控制， 2021， 41（6）： 237-243.

FENG Q S， LIAO C M， ZHANG L， et al. Evaluation of subway vibration influence on human exposure comfort of whole-body vibration [J]. Noise and Vibration Control， 2021， 41（6）： 237-243. （in Chinese）

[2]  赵江涛， 苏洁， 吳奇兵， 等. 地铁运行对沿线不同砌体结构的振动影响研究[J]. 地下空间与工程学报， 2021， 17（5）： 1578-1585， 1612.

ZHAO J T， SU J， WU Q B， et al. Study on the vibration of different types of masonry structures along the metro caused by train running [J]. Chinese Journal of Underground Space and Engineering， 2021， 17（5）： 1578-1585， 1612. （in Chinese）

[3]  KOWALSKA-KOCZWARA A. Impact of selected sources of transport vibrations on the perception of vibrations by people in buildings [J]. Vibroengineering Procedia， 2019， 27： 88-92.

[4]  许暮迪， 袁葵， 花雨萌， 等. 地铁车辆段试车线上盖建筑振动舒适度研究[J]. 世界地震工程， 2021， 37（1）： 137-143.

XU M D， YUAN K， HUA Y M， et al. Research on vibration serviceability of over-track buildings on the test lines of subway depots [J]. World Earthquake Engineering， 2021， 37（1）： 137-143. （in Chinese）

[5]  SANAYEI M， MAURYA P， MOORE J A. Measurement of building foundation and ground-borne vibrations due to surface trains and subways [J]. Engineering Structures， 2013， 53： 102-111.

[6]  ZOU C， WANG Y M， MOORE J A， et al. Train-induced field vibration measurements of ground and over-track buildings [J]. Science of the Total Environment， 2017， 575： 1339-1351.

[7]  SADEGHI J， VASHEGHANI M. Safety of buildings against train induced structure borne noise [J]. Building and Environment， 2021， 197： 107784.

[8]  花雨萌，谢伟平，陈斌. 地铁振动对建筑物竖向楼层响应的影响研究[J]. 建筑结构学报， 2023. 44（3）： 122-129.

HUA Y M， XIE W P， CHEN B. Research on the influence of metro vibration on the vertical floor response of buildings [J]. 2023. 44（3）： 122-129.（in Chinese）

[9]  LOPES P， COSTA P A， FERRAZ M， et al. Numerical modeling of vibrations induced by railway traffic in tunnels： From the source to the nearby buildings [J]. Soil Dynamics and Earthquake Engineering， 2014， 61/62： 269-285.

[10]  GUO T， CAO Z L， ZHANG Z Q， et al. Numerical simulation of floor vibrations of a metro depot under moving subway trains [J]. Journal of Vibration and Control， 2018， 24（18）： 4353-4366.

[11]  KOWALSKA-KOCZWARA A， PACHLA F， STECZ P， et al. Vibration-based damage identification and condition monitoring of metro trains： warsaw metro case study [J]. Shock and Vibration， 2018， 2018： 8475684.

[12]  夏倩， 屈文俊. 地铁振动对既有砌体结构影响规律及因素数值分析[J]. 振动与冲击， 2014， 33（6）： 189-194， 200.

XIA Q， QU W J. Numerical analysis on metro train-induced vibrations and their influences and affecting factors on existing masonry building [J]. Journal of Vibration and Shock， 2014， 33（6）： 189-194， 200. （in Chinese）

[13]  凌育洪， 吳景壮， 马宏伟. 地铁引起的振动对框架结构的影响及隔振研究-以某教学楼为例[J]. 振动与冲击， 2015， 34（4）： 184-189.

LING Y H， WU J Z， MA H W. Effects of subway vibration on a frame structure and its vibration isolation [J]. Journal of Vibration and Shock， 2015， 34（4）： 184-189. （in Chinese）

[14]  YANG J J， ZHU S Y， ZHAI W M， et al. Prediction and mitigation of train-induced vibrations of large-scale building constructed on subway tunnel [J]. Science of the Total Environment， 2019， 668： 485-499.

[15]  马晓磊， 巴振宁， 高愈辉， 等. 滨海软土地区地铁运营对沿线建筑物振动影响分析[J]. 岩土工程学报， 2019， 41（Sup 2）： 177-180.

MA X L， BA Z N， GAO Y H， et al. Vibration effect of metro operation on buildings along Tianjin Binhai New Area in soft soil areas [J]. Chinese Journal of Geotechnical Engineering， 2019， 41（Sup 2）： 177-180. （in Chinese）

[16]  杨觅. 地裂缝场地地铁荷载作用下盾构隧道–地层–地面建筑物振动响应研究[D]. 西安： 长安大学， 2018.

YANG M. Study on vibration response of shield tunnel-stratum-ground building system due to subway train loads in ground fissure site [D]. Xi，an： Chang，an University， 2018. （in Chinese）

[17]  馬蒙， 李明航， 谭新宇， 等. 地铁轮轨耦合不平顺激励对轨道振动影响分析[J]. 工程力学， 2021， 38（5）： 191-198.

MA M， LI M H， TAN X Y， et al. Influence analysis on track vibration due to coupled irregularity excitation of metro wheel-track [J]. Engineering Mechanics， 2021， 38（5）： 191-198. （in Chinese）

[18]  路德春， 马一丁， 王国盛. 近接隧道列车运行时地表振动响应数值模拟[J]. 吉林大学学报（地球科学版）， 2021， 51（5）： 1452-1462.

LU D C， MA Y D， WANG G S. Numerical study on ground surface vibration response under train load in multi adjacent tunnels [J]. Journal of Jilin University （Earth Science Edition）， 2021， 51（5）： 1452-1462. （in Chinese）

[19]  刘维宁， 马蒙. 地铁列车振动环境影响的预测、评估与控制[M]. 北京： 科学出版社， 2014.

LIU W N， MA M. Metro train induced environmental vibrations： prediction， evaluation and control [M]. Beijing： Science Press， 2014. （in Chinese）

[20]  夏志强， 朱林军， 吴福来， 等. 地铁车辆-轨道耦合振动响应分析及轨道结构参数优化[J]. 噪声与振动控制， 2021， 41（2）： 168-173， 189.

XIA Z Q， ZHU L J， WU F L， et al. Analysis of metro vehicle-track coupling vibration responses and optimization of track structure parameters [J]. Noise and Vibration Control， 2021， 41（2）： 168-173， 189. （in Chinese）

[21]  LYSMER J， KUHLEMEYER R L. Finite dynamic model for infinite media [J]. Journal of the Engineering Mechanics Division， 1969， 95（4）： 859-877.

[22]  岳建勇. 地铁交通引起的建筑物振动实测与数值模拟分析[J]. 岩土力学， 2020， 41（8）： 2756-2764， 2784.

YUE J Y. In situ measurement and numerical simulation for the environmental vibration induced by urban subway transit [J]. Rock and Soil Mechanics， 2020， 41（8）： 2756-2764， 2784. （in Chinese）

[23]  ZHENG G， LU P， DIAO Y. Advance speed-based parametric study of greenfield deformation induced by EPBM tunneling in soft ground [J]. Computers and Geotechnics， 2015， 65： 220-232.

[24]  杨龙伟. 地铁振动荷载作用下的地裂缝场地土体振动规律研究[D]. 西安： 长安大学， 2017.

YANG L W. Research on the rule of vibration response of soil under train-induced vibration load in ground fissured area [D]. Xi，an： Chang，an University， 2017. （in Chinese）

[25]  陈俊豪. 地铁沿线建筑物振动与二次噪声相干性及预测研究[D]. 成都： 西南交通大学， 2019.

CHEN J H. Study on coherence and prediction of vibration and re-radiated noise in buildings caused by subway trains [D]. Chengdu： Southwest Jiaotong University， 2019. （in Chinese）