基于模糊PID控制的智能温度控制系统研究
2023-11-24郭志庭
郭志庭
(四川工业科技学院,四川 德阳 618500)
0 引言
温度控制是一种典型的非线性时变控制系统,随着控制理论的发展,将智能控制理论与传统控制理论相结合,从而得到更好的控制效果是技术发展的趋势[1]。传统PID控制器结构简单,有一定的鲁棒性,能够取得较好的控制效果,但传统PID控制器需要根据环境变化,手动调节参数,有一定的局限性,适应性不强[2]。针对传统PID控制器问题,模糊控制系统可以弥补适应性不强的问题,它可以在不需要精确数学模型的情况下,实现对温度的精确控制。该系统利用模糊逻辑理论中的模糊集合、模糊推理和模糊控制等方法,与传统的PID控制器相结合,将模糊的温度信息转化为模糊的控制指令,从而实现对温度的精确控制。
温度模糊控制系统广泛应用于工业自动化、农业生产和生物医学等领域,如农业生产过程中可利用此控制系统提高温室大棚的温度控制精度。目前,该系统研究内容涉及模糊控制算法、模糊控制器设计、模糊控制性能评价等方面[3-5]。近年来,随着计算机技术的快速发展,温度模糊控制系统的研究也日益深入,不断涌现出新的理论和方法,为实现更加精确的温度控制提供了有力支持。
1 传统PID控制器原理
在模拟控制系统中,其过程控制方式是将被测参数温度由传感器换成统一的标准信号送入调节器。在调节器中与给定值进行比较,然后把比较的差值经PID运算后送到执行机构,改变进给量,以达到自动调节的目的[6-7]。PID控制系统原理如图1所示。
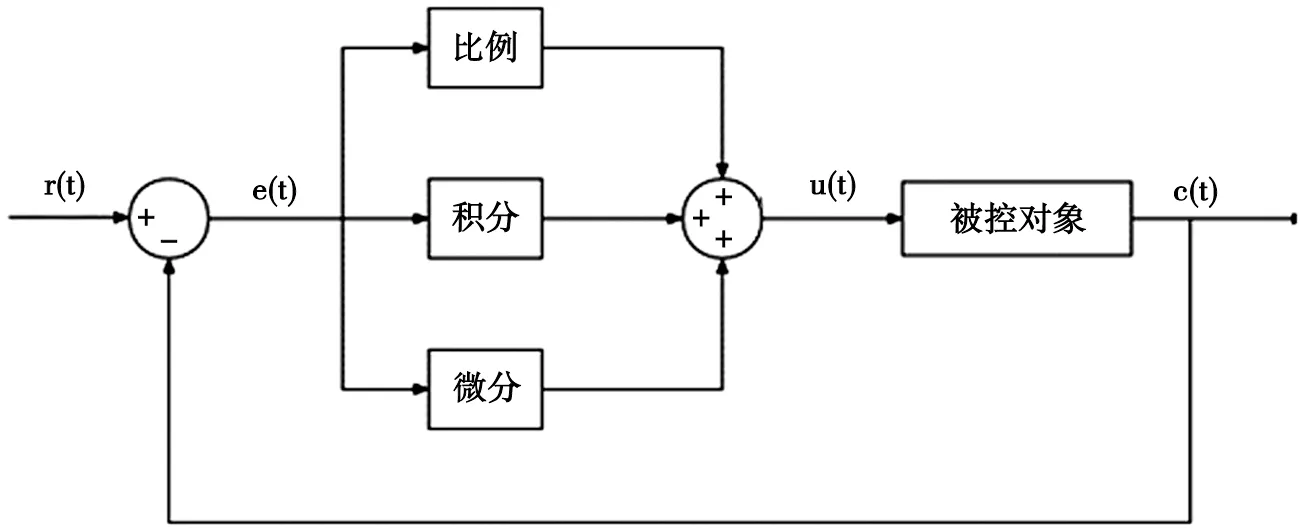
图1 PID控制原理图
PID是一种线性控制器,根据输出值c(t)和输入值r(t)的偏差构成控制方案
e(t)=r(t)-c(t)
(1)
其控制规律为
(2)
对公式(2)进行拉普拉斯变换,求解出传递函数,如公式(3)所示
(3)
比例环节可以成比例地反映控制系统的偏差信号e(t),偏差一旦产生,控制器立刻产生控制作用,以减小偏差;积分环节主要用于消除静差,提高系统的无差度。积分作用的强弱取决于积分时间常数TI,TI越大积分作用就越弱,TI越小积分作用就越强。微分环节反映偏差信号的变化趋势,并能在偏差信号变得太大之前在系统中引入一个有效的早期修正信号,从而加快系统的动作速度,减少调节时间[8]。
2 模糊控制原理
计算机处理问题的逻辑是根据事先确定的信息,按照既定的方法步骤,做出判断和处理问题。但人的思维方式可以在只得到少部分信息的情况下,对问题进行分析和处理[9]。为了能够让计算机处理问题的思维方式模仿人的这种模糊判断思维,则需要把人语言中所具有模糊、不确定信息以定量的形式表现出来,模糊的概念由此而来。模糊集合是一个特性的对象对于给定集合的一个隶属度,是处于0~1之间的某个值,而不限于0和1这两个值。这样描述更自然,更接近人的思维表达方式。模糊规则是在模糊集的基础上,结合操作经验、表述知识,构成的一组控制逻辑规则[10-11]。基于模糊规则构成的模糊控制系统表达了输入、输出的映射关系。通过以上的处理,模糊控制系统可以向任意函数关系逼近。模糊控制器的基本流程图如图2所示。
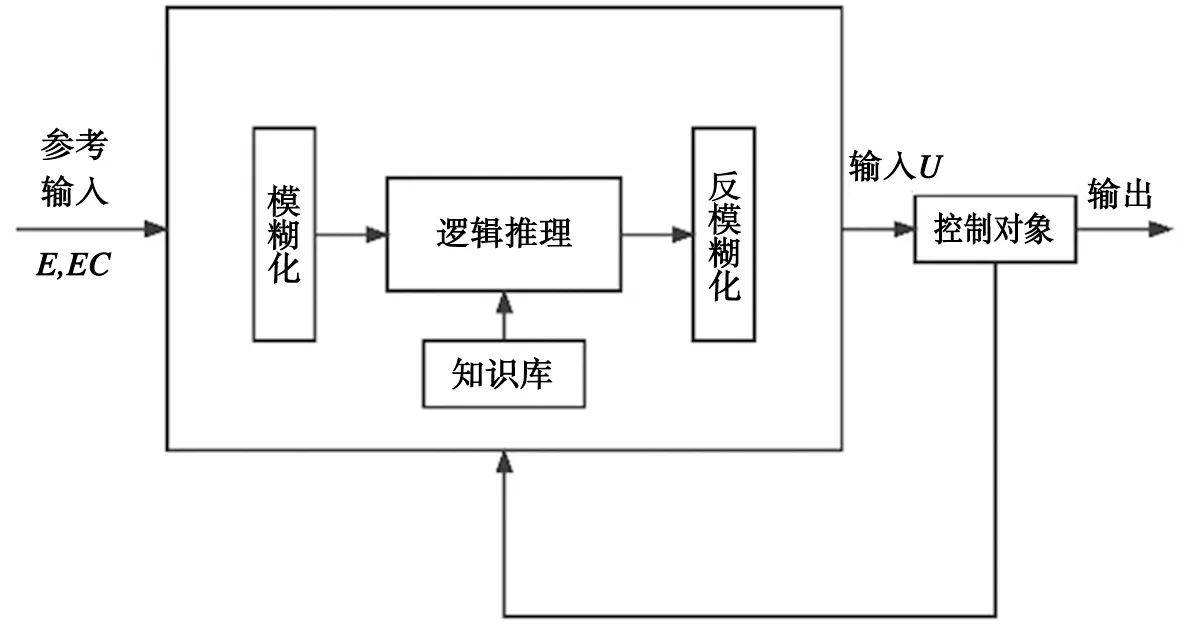
图2 模糊控制器基本流程图
从图2中可以得出输入变量为输入误差E与输出误差变化率EC,而控制变量则为下一个状态输入U。其中E、EC、U统称为模糊变量;模糊化将输入值E、EC以适当的比例转换到论域的数值,利用口语化变量来表述测量物理量的过程,依照适合的语言值求得该值相对应的隶属度,此口语化变量称之为模糊子集合;知识库提供了处理模糊数据的相关定义,还提供了由一群语言控制规则描述的控制目的和策略;逻辑推理是模仿人操作经验的模糊概念,运用模糊逻辑和模糊推论法进行推论,得到模糊控制信号;反模糊化将推论所得到的模糊信号转换为明确的控制信号,作为系统的输入值。
3 基于模糊PID控制的智能温度控制系统模型设计
3.1 温度控制对象模型确定
温度控制系统的对象特点为非线性及滞后性,根据频率响应特性得到温度控制对象的传递函数为式(4)
(4)
3.2 基于模糊PID控制的智能温度控制系统结构
图3为模糊PID控制的智能温度控制系统基本结构图。
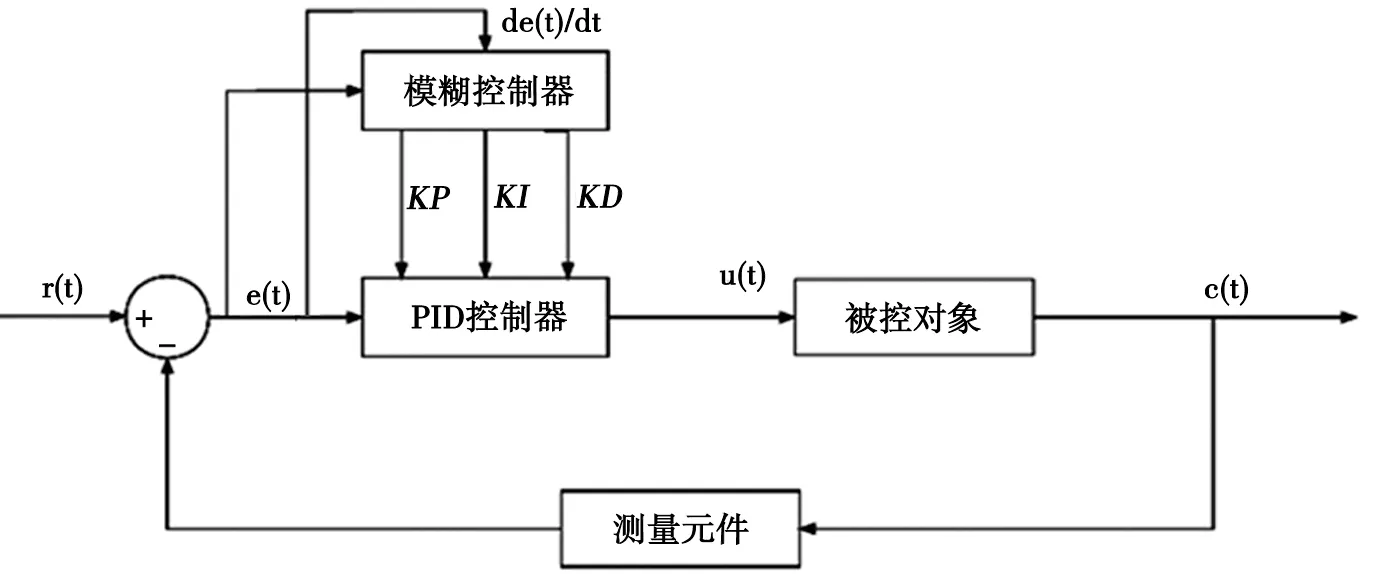
图3 模糊PID控制的智能温度控制系统基本结构图
从图3可以看出该控制模型是基于经典PID控制调节器结构,在此基础上,添加了模糊控制器,其中,输入变量为温度偏差e(t)和偏差变化率de(t)/dt,输出变量为PID控制器的三个控制参数KP、KI、KD。由模糊控制理论与传统控制相结合,提出由专家经验形成的模糊规则对控制系统推理判断,输出给传统PID调节器,从而实现了对温度的模糊控制。
3.3 模糊规则的制定
由传统PID控制器原理和参数KP、KI、KD对控制因素的影响,结合专家经验,制定模糊规则如下:
1)当E<0,EC>0时,应尽快消除偏差,加大偏差的权值,接近稳态后,加大偏差变化的权值,适当减少积分作用。
2)当E<0,EC<0时,应尽力减小超调,加大偏差变化的权值。
3)当E>0,EC<0时,系统基本稳态,应减少控制作用。
4)当E>0,EC>0时,保持微分参数,使系统快速稳定。
系统稳定后,恢复调整PID参数。基于上述规则,建立模糊控制表,放入模糊控制器中,实现温度模糊控制。
4 仿真分析
4.1 仿真模块建立
本文采用Matlab Simulink环境下,建立模型,输入模糊逻辑控制规则,仿真分析。图4为基于模糊PID的温度控制系统模型图。

图4 基于模糊PID的温度控制系统模型图
为了便于比较,在图4的模型中放入了传统PID模型,传统PID模型如图5所示。
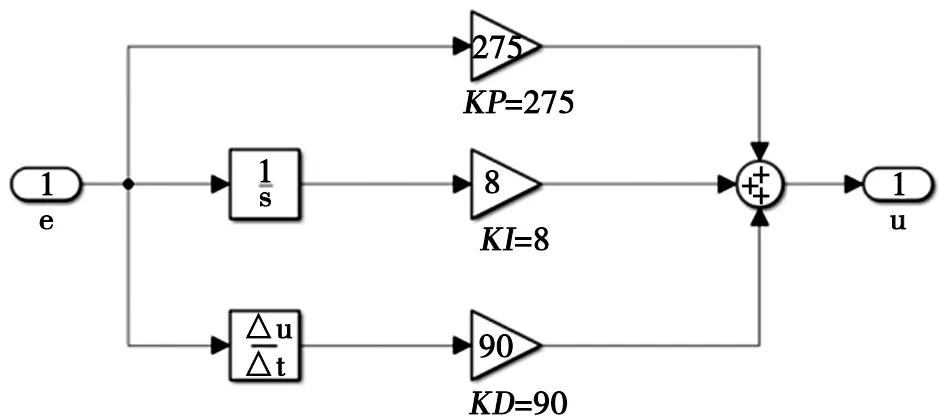
图5 传统PID模型
在模糊PID控制中,加入了模糊逻辑控制器,模糊逻辑控制器根据输入及模糊规则实时矫正PID参数送到PID控制系统中,图6为模糊PID模型。
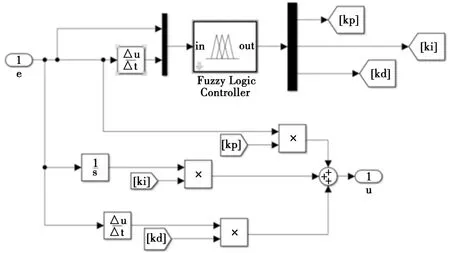
图6 模糊PID模型
4.2 模糊规则建立
利用Matlab模糊模块,将模糊规则输入模糊逻辑控制器,首先建立2输入3输出隶属度函数,图7为模糊逻辑输入输出图。

图7 模糊逻辑输入输出图
根据仿真测试和模型特性确定输入量E和EC及输出量KP、KI、KD的范围。图8为输入量E的设置图,从图中可以看出,将输入量E分为NB、NM、NS、Z、PS、PM、PB几个等级,其中NB和PB设置为gaussmf类型,其余等级设置为trimf类型。
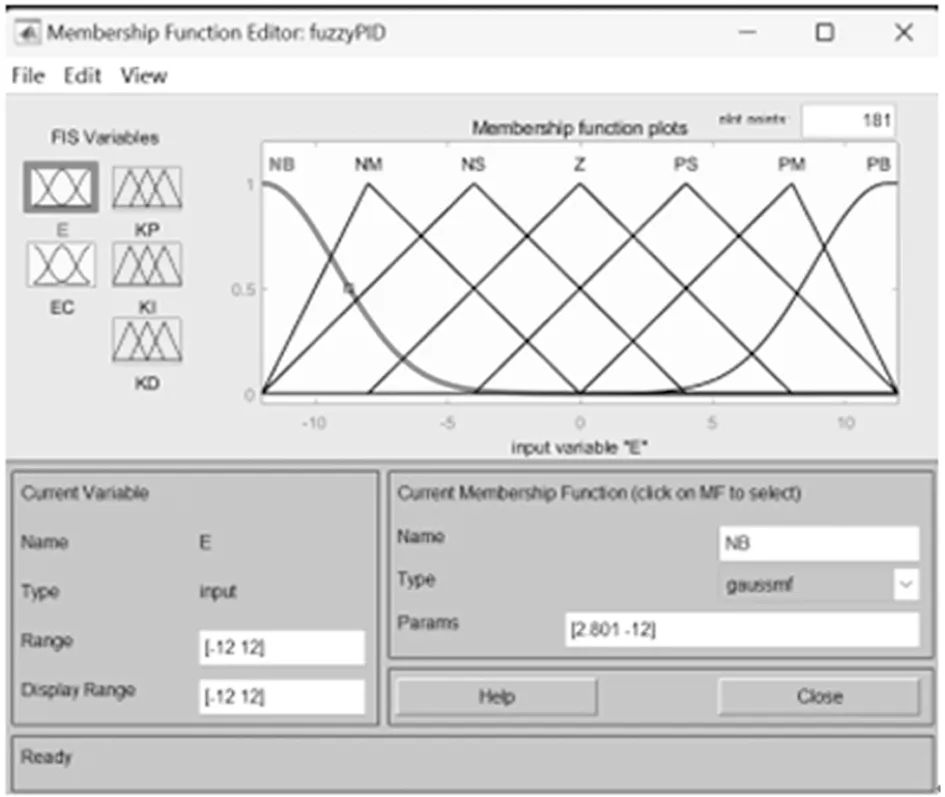
图8 输入量E设置图
[Input1]
Nanes=‘E’
Range=[-12 12]
NumMFs=7
MF1=‘NB’:‘gaussaf’,[2.801-12]
MF2=‘NM’:‘trimf’,[-12 -8 0]
MP3=‘NS’:‘trimf’,[-12 -4 4]
MF4=‘Z’:‘trim’',[-8 0 8]
MF5=‘PM’:‘trimf’,[o 8 12]
MF6=‘PB’:‘gauss2mf',[2.801 11.6 1.362 12.4]
MF7=‘PS’:‘trimf’,[-4 4 12]
通过以上设置可以使得输入E更为平滑。其他输入和输出,仍按上述步骤,根据数据特性分别进行设置。
完成输入输出参数设置后,接下来根据上节中提到的整定规则,制定模糊控制规则,如图9所示。
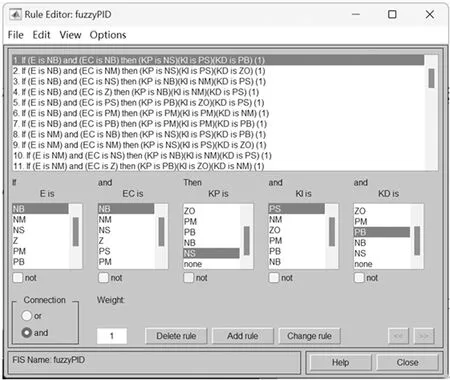
图9 模糊规则设置图
通过模糊规则,可以得出输出值所对应的隶属度,同时,可通过曲面观测器来查看模糊规则推理和输出曲面(图10)。
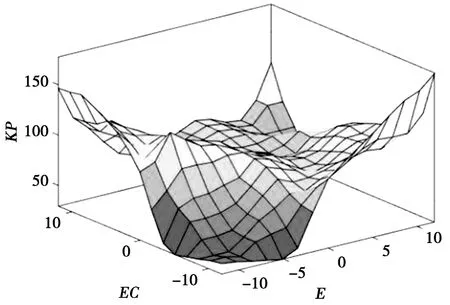
图10 模糊规则曲面观测器
4.3 仿真结果分析
建立并输入模糊控制规则后,对模型进行仿真分析,结果如图11所示。
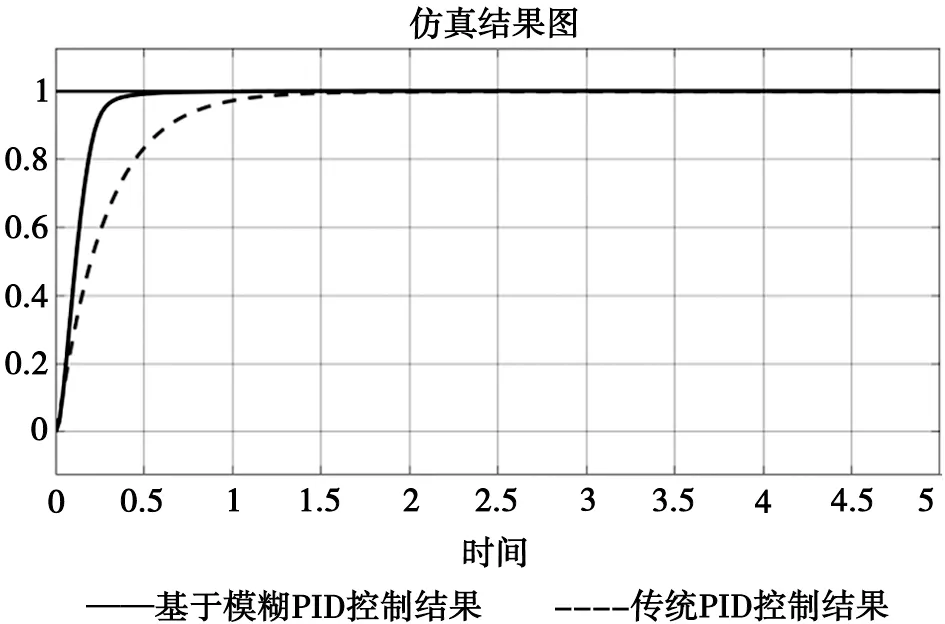
图11 仿真结果图
从图11中可以看出基于模糊PID控制到达稳态时间要比传统PID控制到达稳态时间短。通过示波器工具调用分析,实测基于模糊PID控制到达稳态时间为0.716 s,基于传统PID控制到达稳态时间为1.827 s。通过仿真试验验证了模糊PID控制上升时间更短,控制更为稳定,且鲁棒性更强。
5 结论
本文将模糊控制与传统PID控制器相结合,构建模糊PID智能温度控制系统,即根据当前系统误差E和误差变化率EC,通过模糊控制系统的模糊规则,动态调整PID参数。采用Matlab模糊控制工具箱进行仿真试验,验证了模糊PID智能温度控制系统能实现动态参数调整,上升时间更短,控制更为稳定,且鲁棒性更强。
