柔索驱动拣矸机器人分拣轨迹跟踪控制研究

刘 鹏，龚 莉，马宏伟，曹现刚，张旭辉，乔心州，夏 晶

（1.西安科技大学 陕西省矿山机电装备智能监测重点实验室,陕西 西安 710054；2.西安电子科技大学 “电子装备结构设计”教育部重点实验室,陕西 西安 710000）

0 引言

煤炭是我国最主要的一次能源，在我国经济发展中占有举足轻重的地位。同时，随着全球气候问题日益突出，保护环境迫在眉睫。在煤炭生产过程中，原煤中不可避免地混有矸石。矸石不仅发热值低，还是主要的环境污染源之一，因此将矸石从原煤中分选出来是提高原煤质量，实现煤炭清洁利用的关键环节。智能化煤矿需要重点建设十大智能系统，其中煤炭分选智能化建设是煤矿智能化建设的一项主要内容[1]。针对煤矸石分拣难题，曹现刚等[2]设计了基于卷积神经网络的煤矸识别定位系统，识别出的目标矸石需要通过机器人进行自动化分拣。但目前依旧采用人工分拣的方式完成，机器人完成矸石分拣工作也处于起步和探索阶段。柔索驱动并联机器人具有诸多优点而被广泛应用于风洞实验[3]、天文观测[4]、3D 打印[5]以及高空摄像[6]等诸多领域。结合柔索驱动并联机器人的构型特点与优势，笔者设计了一种4 柔索驱动的3 自由度柔索驱动拣矸机器人[7-9]，该机器人横跨于带式输送机上方，通过4 根柔索的协调收放驱动末端抓斗在三维空间运动，实现煤矸石的精准抓取和自动化分拣。然而，采用柔索驱动并联机器人完成动态目标矸石的分拣工作势必面临着许多新的挑战。一方面，由于柔索的柔性、弹性、非线性和单向约束特性，以及抓矸置矸过程的动态冲击等扰动影响，很难精确获取拣矸机器人的动力学模型；另一方面，柔索驱动力的单向约束特性决定了拣矸机器人末端抓斗在分拣运动过程中必须时刻保持张紧，否则就会发生柔索的松弛，破坏机器人构型，导致目标矸石的分拣任务无法顺利完成。拣矸机器人分拣轨迹跟踪控制解决的问题是如何补偿和抵消未能精确建模的动力学、抓矸置矸过程的动态冲击、复杂环境所带来的外部扰动等因素影响，使机器人末端抓斗能够按照既定的轨迹平稳运行，完成动态目标矸石的分拣工作。因此保证拣矸机器人末端抓斗的精准轨迹跟踪运动控制及其稳定性成为需要解决的关键难题。

采用柔性和仅能单向受力的柔索驱动末端执行器运动，使柔索驱动并联机器人的控制面临着诸多严峻挑战，国内外诸多学者致力于柔索驱动并联机器人运动控制方面的研究，所采用的控制算法包括鲁棒控制[10]、计算力矩控制[11]、反馈线性化控制[12]、滑模控制[13]、自适应控制[14]、神经网络控制[15]以及模糊控制等[16]。OYMAN 等[17]基于阻抗控制方法对柔索驱动康复机器人进行控制，并通过试验和仿真验证了控制器的有效性。KHALILPOUR 等[18]采用集中质量法建立了柔索动力学特性的柔索驱动并联机器人动力学模型，依据机器人动力学模型设计了鲁棒无源控制器，证明了所设计控制系统的稳定性。YANG 等[19]针对柔索驱动康复机器人的运动控制问题，设计了能够识别康复者运动意图的力位混合控制策略，并通过试验验证了所设计的控制器能够连续的识别康复者的运动意图，保证了机器人有更好的运动性能。ZI[20]基于拉格朗日方程建立了四索驱动机器人动力学模型，设计了自适应模糊控制系统，采用Lyapunov 方法证明了控制器的稳定性，并通过仿真验证了所设计控制系统的有效性。KUMAR 等[21]提出采用输入-输出反馈线性化方法对欠约束柔索驱动并联机器人进行控制，通过仿真验证了该控制方法的有效性。张立勋等[22]提出了基于柔索驱动的宇航员深蹲训练机器人，提出了包含多余力补偿力伺服控制策略，并通过试验验证了所提出控制策略具有较好的控制效果。SEYFI 等[23-24]将鲁棒控制方法应用到柔索驱动并联机器人的运动控制中，设计了一种带补偿效果的类计算力矩控制器，并通过仿真说明了所设计的鲁棒控制器对模型不确定性和外界扰动具有很好的控制效果。SHANG等[25-26]考虑柔索驱动并联机器人各支链运动误差对末端执行器运动控制的影响，设计了自适应同步控制器对机器人末端执行器的运动轨迹进行跟踪控制，并通过仿真和试验验证了自适应同步控制器具有较好的轨迹跟踪效果。KORAYEM[27]提出了一种移动的柔索驱动并联机器人，建立了该机器人的运动学和动力学模型，设计了输入-输出反馈线性化控制系统，并通过仿真和实验验证了所设计控制系统的有效性。

上述文献针对柔索驱动并联机器人控制困难的问题，采用不同方法实现了机器人末端执行器的高性能轨迹跟踪控制。柔索驱动拣矸机器人属于多输入多输出的复杂非线性系统，其末端抓斗必须跟随皮带运输机运动，并在运动过程中完成煤矸石的分拣工作，传统控制方法如PID 控制以及计算力矩控制等方法，很难取得良好的控制效果。柔索驱动拣矸机器人需要根据预定运动轨迹平稳地完成拣矸任务，控制系统的设计是至关重要的。由于柔索的单向受力特性，其易受外部冲击载荷等外部载荷的干扰。因此，考虑补偿外部干扰的控制策略，是保证柔索驱动拣矸机器人顺利完成拣矸任务的关键。随着诸如模糊控制、神经网络控制等诸多智能控制方法的发展与应用，复杂非线性系统的控制得到了较好的解决[28-30]。针对矸石分拣过程中存在的动力学模型不确定以及外部扰动问题，采用模糊控制方法对扰动项进行逼近，并采用变结构鲁棒性对模糊控制系统的逼近误差进行补偿，提出柔索驱动拣矸机器人的自适应模糊鲁棒抓取轨迹跟踪控制策略，实现拣矸机器人末端抓斗的精准跟踪控制，为顺利完成矸石分拣任务奠定坚实基础。

1 拣矸机器人系统方案与模型

1.1 系统方案

如图1 所示，矸石分拣机器人系统由柔索驱动拣矸机器人、带式输送机以及煤和矸石、机器视觉系统、位置传感与检测系统、矸石回收仓等组成。柔索驱动拣矸机器人为矸石分拣机器人系统的执行机构，包括机械模块和控制模块2 部分。其中，机械模块包括定机架、滑轮、电机-柔索驱动系统、末端抓斗、连接柔索与末端抓斗的点状铰链等组成；控制模块由工业计算机、运动控制器、激光跟踪仪、编码器等组成。采用机器视觉系统获取待抓取目标矸石位置和维度信息，目标矸石的质量可以通过其形状和尺寸进行估算。同时，采用3D 激光跟踪器与伺服电机编码器获得末端抓斗的空间三维位置。基于上述测量系统和设备，对机器人末端抓斗采用闭环控制，从而精确地执行目标矸石的精准轨迹跟踪控制与可靠分拣操作。

图1 拣矸机器人系统方案Fig.1 Scheme of the cable-driven gangue sorting robot

拣矸机器人横跨于带式输送机上方，通过电机协调驱动4 根柔索的收放，驱动末端抓斗运动到目标矸石所在位置的邻域内，并抓取矸石，将矸石送至矸石回收仓，重复上述分拣过程，完成目标矸石的分拣工作。根据拣矸置矸作业过程和特点，将机器人末端抓斗的分拣轨迹分为4 个阶段，即启动段、准备段、抓矸段以及置矸段[31]。文献[31]对柔索驱动拣矸机器人分拣轨迹规划进行了深入研究，得到了能够保证末端抓斗光滑连续运行的分拣轨迹，为机器人的运动控制奠定了基础。目标矸石的分选过程如下：首先，与带式输送机同步运动的目标矸石将进入视觉识别区，机器视觉系统识别并采集目标矸石的形状和位置信息，并将其传送给机器人的主控制器；其次，目标矸石移动一段时间到达拣选区域，机器人末端抓斗在此执行目标矸石的抓取操作；最后，目标矸石被放入矸石回收仓，完成目标矸石的抓取和分拣工作。机器人末端抓斗回到零位，继续完成后续矸石的分拣任务。

1.2 运动学与动力学模型

机器人运动学模型是机器人轨迹规划、动力学模型以及运动控制的基础。采用矢量封闭原理建立拣矸机器人索长空间与末抓斗空间的运动学模型。图2 为柔索驱动拣矸机器人运动学简图，a，b和h分别表示柔索驱动拣矸机器人空间结构尺寸。根据柔索驱动拣矸机器人几何构型，用Ai(xi,yi,zi)，(i=1,2,3,4)表示4 根立柱顶端滑轮的圆心，以A1立柱底部为坐标原点，建立全局坐标系o-xyz。

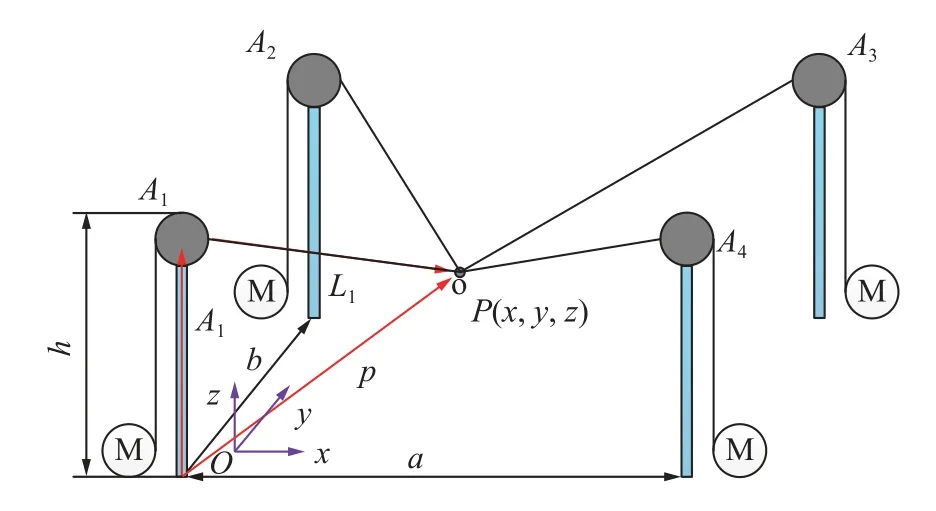
图2 柔索驱动拣矸机器人运动学简图Fig.2 Kinematics schematic of the cable-driven gangue sorting robot

则各根柔索索长可表示为

式(1)描述了柔索驱动拣矸机器人末端抓斗空间与索长空间的映射关系。当给定拣矸机器人末端抓斗的空间运动轨迹x,y,z，基于式(1)可求得其对应的索长变化。

柔索驱动力方向的单位向量可以表示为

柔索驱动拣矸机器人动力学模型是实现末端抓斗精准跟踪控制的基础和前提。建立机器人动力学模型常用的包括牛顿-欧拉法、拉格朗日方程、虚功原理等。本文采用牛顿-欧拉法建立柔索驱动拣矸机器人的动力学模型，以拣矸机器人末端抓斗为研究对象，设施加于末端抓斗上的各柔索驱动力为Ti，则末端抓斗受力如图3 所示。因此，根据牛顿-欧拉法可得机器人末端抓斗的动力学方程：

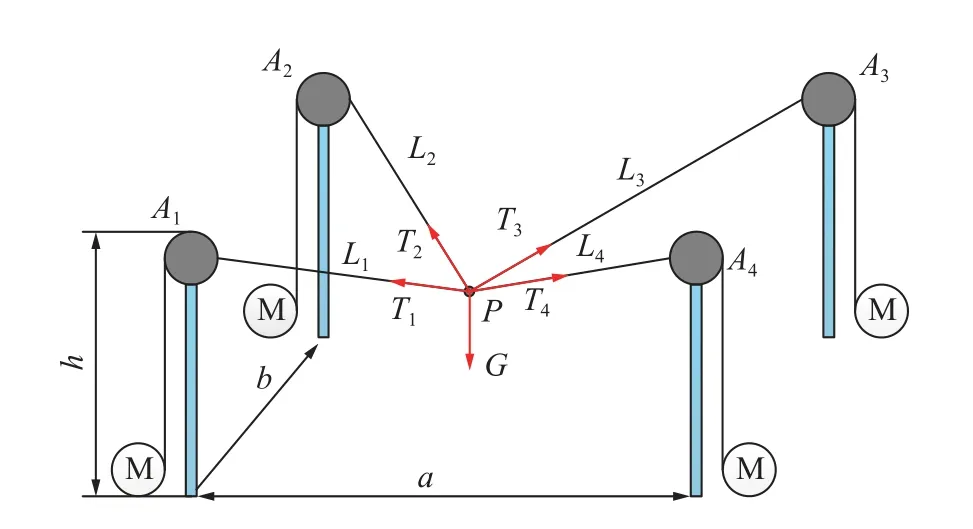
图3 柔索驱动拣矸机器人动力学简图Fig.3 Dynamics schematic of the cable-driven gangue sorting robot

式中：m为末端抓斗的质量分别表示机器人末端抓斗沿着3 个方向的加速度；g为重力加速度。

可以将方程式(3)的动力学模型写成如下简化形式：

由于柔索的柔性和单向受力特性，以及抓矸置矸过程中动态冲击等影响，机器人在执行目标矸石分拣任务的过程中，很难精确获取机器人的动力学模型。且上述参数的改变势必影响机器人的控制性能。因此，综合考虑机器人动力学模型参数的变化和外部扰动，拣矸机器人实际的动力学模型可以表示为

式中：M(X)=M0+ΔM和H(X)=H0+ΔH为拣矸机器人实际的动力学参数，M0和H0分别为质量矩阵和哥氏力、向心力以及重力的估计值，ΔM和ΔH为建模误差，τd为外部扰动，f为摩擦力项。

因此，柔索驱动拣矸机器人实际的动力学模型可以表示为

式中：D=+ΔH+f+τd为复合扰动项，包括了建模误差、摩擦力和外部扰动等。

由于τ项中J为非方阵，使得机器人动力学方程式解不唯一，而机器人控制需要实时获取柔索驱动力。因此，需选择合适的优化指标和方法对柔索拉力进行优化求解。采用广义逆矩阵、零空间基底对柔索驱动力进行优化，获取柔索驱动力的优化解[6,32-33]。

2 拣矸机器人分拣轨迹跟踪控制策略

由于柔索单向受力特性，机器人运行过程中易受外部冲击载荷等外部干扰的影响，本节采用模糊控制和鲁棒控制思想，根据动力学模型式(6)，为末端抓斗的轨迹跟踪运动设计鲁棒自适应模糊追踪控制器，保证机器人末端抓斗的精准轨迹跟踪控制。本文所设计的控制器采用模糊控制系统逼近动力学模型式(6)中的复合扰动项，并设计鲁棒项消除逼近误差，以达到精准的轨迹跟踪控制。

模糊逻辑控制系统是基于L.A.Zadeh 提出的模糊集合理论，在模糊数学的基础上，建立起来的控制系统，其主要由模糊化接口、模糊知识库、模糊推理机和模糊判决4 个基本单元组成，相较于传统的控制方法，其具有明显的优越性，特别是智能控制方面其控制效果显著。

模糊逻辑控制系统可以用来逼近假设模糊逻辑系统是模糊集U⊆Rn到模糊集V⊆Rm的映射，则整个模糊规则库包含的模糊关系可表示[34-35]为

因此，模糊系统的非线性映射可表示为

根据公式(12)，则模糊控制系统的输出可以表示为

柔索驱动拣矸机器人的控制系统的任务是：计算作用于机器人末端抓斗的柔索驱动力T，保证末端抓斗在运行过程中的实际位置X趋近于期望值Xd。因此，定义拣矸机器人，末端抓斗轨迹跟踪误差为

式中：X为末端抓斗的实际位置；Xd为末端抓斗的期望位置。

定义滑模函数如下：

式中，Λ为正定矩阵。

定义参考跟踪速度：

为了保证拣矸机器人末端抓斗的精准运动控制，根据机器人动力学模型，设计鲁棒自适应模糊控制律为：

采用Lyapunov 方法证明所设计控制策略式(17)对于拣矸机器人动力学模型式(6)是稳定的。

依据鲁棒自适应模糊控制律(17)，定义Lyapunov 函数：

由式(18)和式(21)可知：Lyapunov 函数V(t)为正定，且Lyapunov 函数的导数(t)为负定。由Lyapunov 稳定性理论可得所设计控制策略是稳定的，能够实现对拣矸机器人末端抓斗的精准控制。

3 仿真分析

本章所有算例的仿真均在MATLAB®2020a Simulink 下完成。拣矸机器人分拣轨迹跟踪控制器Simulink 模型如图4 所示。取模糊自适应控制策略的隶属度函数为其中分别为0、1、2、3、4，i=1，2，··，5。Ai分别为NB、NS、ZO、PS 和PB。取复合扰动项D=[4sin(10t) 2sin(10t)4sin(10t)]T，W=[0.2 0 0;0 0.2 0;0 0 0.2]，Γ=diag(10,10,10)×10-4，KD=250I。柔索驱动拣矸机器人结构参数a=4 m，b=4 m，h=3 m，m=5 kg，g=9.8 N/kg。

图4 鲁棒自适应模糊控制器Simulink 模型Fig.4 Simulink model of the proposed robust adaptive fuzzy controller

采用空间螺旋线和文献[31]所提出的分拣轨迹对所设计的鲁棒自适应模糊追踪控制器性能进行仿真验证。为了说明文中所设计控制策略的有效性和优越性，将文中所设计的控制策略与文献[20]的模糊控制器进行对比。因此，将文献[20]中设计的控制律应用于柔索驱动拣矸机器人，可以表示为

此外，提出最大跟踪误差和均方根误差两个指标定量评价上述两个控制器的控制性能，分别表示为

式中：e(k)为拣矸机器人末端抓斗的位置跟踪误差，N和k分别为轨迹离散个数和当前采样点。

3.1 算例1

当拣矸机器人末端抓斗的期望轨迹为上述螺旋线时，采用鲁棒自适应模糊控制律对末端抓斗的运动轨迹进行跟踪控制，图5 为仿真得到期望螺旋线轨迹与实际轨迹三维图。从图中可以看出：采用本文所提出的鲁棒自适应模糊控制策略，保证了柔索驱动拣矸机器人末端抓斗的运动具有良好的轨迹跟踪效果。

图5 末端抓斗空间螺旋线轨迹与跟踪轨迹Fig.5 Spatial spiral and trajectory tracking of the end-grab

拣矸机器人末端抓斗沿着x、y和z三个方向期望位移和实际位移、位移跟踪误差如图6 所示。从上述轨迹跟踪曲线可以看出：采用鲁棒自适应模糊控制策略，沿着末端抓斗运行的3 个方向均能够获得较好的位置跟踪效果。相较于中间位置点，轨迹曲线起始点的跟踪效果是最差的。通过图6d 可以发现：x、y和z三个方向在最初的0～0.5 s 左右的波动呈现出不稳定的现象，但随后均保持稳定变化，表明所提出控制策略的有效性和稳定性；相较于x和y方向，z方向的跟踪效果最佳，其误差绝对值不超过3‰，且z方向的误差明显按固定周期先变小后变大的趋势稳定变化；x和y方向误差绝对值均在6‰以内，波动绝对值不超过3‰，且误差明显按固定周期在上述范围内稳定变化。

图6 x、y 和z 方向位置跟踪与跟踪误差Fig.6 x,y and z-direction position tracking and tracking errors for the spatial spiral

拣矸机器人末端抓斗沿着x、y和z三个方向的速度跟踪误差的变化曲线如图7 所示。从图7 可以看出：x、y和z三个方向速度跟踪误差在最初的0～0.5s 左右的波动呈现出不稳定的现象，但随后均保持稳定变化。其中x方向速度误差绝对值在1.6%以内，y方向速度误差在1.6%以内，z方向速度误差在1.5%以内。对于图7b，在初始时刻，y方向期望速度存在直线上升的情况，这是Simulink 模块中sin 函数求导本身导致的问题，这也导致了图7e最初的速度误差达到了32%，之后其保持稳定波动。

图7 x、y 和z 方向速度跟踪误差Fig.7 x,y and z-direction velocity tracking errors for the spatial spiral

被控量柔索拉力Ti(i=1,2,··,4)随时间变化如图8 所示。其结果表明：4 根柔索的驱动力变化连续，均介于10～40 N 之间，满足柔索单向受力特性。且被控量柔索拉力的波动，其相位、周期和波动范围均稳定变化。

图8 空间螺旋轨迹下四根柔索的驱动力Fig.8 Four cable tensions for the spatial spiral

3.2 算例2

本章节选用文献[31]所提出的4 段式分拣轨迹作为期望轨迹，采用鲁棒自适应模糊控制策略控制末端抓斗运动，说明所提出控制策略的有效性和稳定性。拣矸机器人末端抓斗初始运动状态设置为：仿真时间为4 s。

图9 所示为采用文中所提控制策略跟踪4 段式分拣轨迹，仿真得到的期望轨迹与实际轨迹三维图。从图中可以看出：采用鲁棒自适应模糊控制策略控制柔索驱动拣矸机器人末端抓斗的运动，其轨迹跟踪效果良好。

图9 期望轨迹与实际轨迹三维图Fig.9 Three-dimensional diagram of the expected pick-andplace trajectory and trajectory tracking

柔索驱动拣矸机器人末端抓斗沿着x、y和z三个方向的位置误差如图10 所示。从图中可以看出：x，y和z三个方向误差绝对值均在2‰以内，其中y方向的误差最大，其误差最大绝对值在3.8 s 左右达到了1.75‰。根据文献[31]所提出轨迹规划方案，此时已处于分拣轨迹置矸段，末端抓斗已经空载，其不影响柔索驱动拣矸机器人的平稳运行。

图10 x、y 和z 方向位置误差Fig.10 x,y and z-direction position tracking errors for the pickand-place trajectory

将文中所提出的鲁棒模糊控制器与文献[20]所提出的控制器性能进行对比，分别采用公式(23)和(24)计算最大跟踪误差和均方根误差2 个指标，其结果见表1。从表中数据可以看出：文中提出的鲁棒模糊控制器比文献[20]所提出控制器具有更好的轨迹跟踪精度和跟踪效果。采用2 个控制器所得到的最大跟踪误差相同，是因为仿真过程中末端抓斗的初始状态设置为相同，且最大跟踪误差发生在轨迹初始点，因此，两者具有相同的MAE 值。

表1 两个控制器性能指标RMSE 和MAE 的对比Table 1 Comparison of RMSE and MAE for the both controllers

图11 给出了拣矸机器人跟踪4 段式分拣轨迹过程中的速度跟踪及速度跟踪误差。从图中可以看出：x，y和z三个方向的速度跟踪效果良好，跟踪效果最差的区域位于轨迹起始处与极值处，但总体效果良好。x，y和z三个方向的速度误差绝对值在1.8%以内。1.8～3.2 s，速度波动最为复杂，但此时末端抓斗处于抓矸段，相较于其他阶段，该阶段末端抓斗的运动较复杂，但从图中可知速度误差最大波动绝对值约为0.75%。

图11 x、y 和z 方向速度跟踪及速度跟踪误差Fig.11 x,y and z-direction velocity tracking and velocity tracking errors

图12 为采用鲁棒自适应模糊控制策略情况下，被控量柔索驱动力Ti(i=1,2,··,4)随时间的变化图。从图中可以看出：柔索驱动力均介于5～100 N，满足柔索单向受力特性。虽然2.4～2.8 s 内，1 号与4 号柔索驱动力存在尖点情况，但其仍然是连续变化，不会造成冲击。此外还发现，1 号与4 号柔索，2 号与3 号柔索驱动力从2.3 s 开始两两按相同变化规律变化，这与柔索驱动拣矸机器人的对称关系式相符合。

图12 分拣轨迹下4 根柔索的驱动力Fig.12 Four cable tensions for the pick-and-place trajectory

通过上述轨迹跟踪仿真结果可以看出：拣矸机器人末端抓斗轨迹跟踪控制效果良好，在保证末端抓斗位于最小索拉力工作空间中时，被控量柔索拉力均大于最小索拉力5 N，且均在合适的范围内波动，速度跟踪效果也较好。

4 结论

1) 考虑拣矸置矸过程中的动态冲击以及外部干扰，基于牛顿-欧拉法建立了柔索驱动拣矸机器人的动力学模型；设计了能够保证拣矸机器人末端抓斗高性能轨迹跟踪控制的鲁棒自适应模糊控制器，并基于Lyapunov 稳定性理论证明了所设计控制系统的稳定性。

2) 以空间螺旋线轨迹和作者所提出的4 段式实用分拣轨迹为末端抓斗的期望运动轨迹，对柔索驱动拣矸机器人控制系统进行了仿真分析。仿真结果表明：拣矸机器人末端抓斗的位置跟踪和速度跟踪效果良好，误差均在可接受范围内；且被控量柔索驱动力均满足柔索的单向受力要求。说明了文中所提出的模糊鲁棒自适应控制策略对柔索驱动拣矸机器人的轨迹跟踪控制有效且可靠。

对比文献[20]提出的控制器，所提出的鲁棒自适应模糊控制器具有更好的位置跟踪和速度跟踪效果。下一步，将在试验样机上对所提控制方法和控制策略进行试验验证，并进行选煤现场的工业试验。