短柱型钛合金帽型加筋结构极限承载能力分析方法

2023-11-23吉国明王睿文眭相映

科学技术与工程 2023年30期

吉国明,王睿文,眭相映

(西北工业大学航空学院,西安 710072)

加筋结构具有刚度大、结构效率高、质量轻等优点,其通常情况是由主体结构(壳或层合板)和加强筋(金属、非金属或复合材料)通过各种连接方式 (焊接、铆接、超塑成形)连接而成的。在薄壁结构上布置筋条,能在不明显增加结构重量的前提下,极大地提高薄板的抗弯刚度,是提高薄壁结构力学性能的重要方法之一。加筋结构在飞机结构中应用十分广泛,在轴向压缩载荷下,结构容易发生屈曲现象,但屈曲并不意味着已被破坏,随着轴向载荷的继续增大,大多数加筋结构还是有一定的承载能力,即后屈曲阶段[1]。在保证安全的前提下,充分利用加筋结构的后屈曲承载能力要比加密桁条或者增加蒙皮的厚度更加切合轻量化设计原则[2]。

目前中外学者对加筋结构在轴压情况下的极限承载能力研究取得了一定的成果。张侃等[3]采用板元法和切割法分别对铝锂合金2099-T83进行了计算,并对飞机设计手册中的切割法做出了一定的修改,得到了较好的效果;朱熠凡等[4]通过Abaqus有限元软件分析了悬挂式铝合金整体壁板在轴向压力下的应力分布情况,并分析了模型大小、初始缺陷、横梁刚度、侧向压力等因素对其极限承载力的影响;王维阳等[5]研究了帽型复合材料加筋壁板层合板屈曲及后屈曲的极限承载能力研究;李真等[6]结合了工程上的常用分析思路,数值模拟分析和具体试验操作3种方法,分析了压缩载荷作用下复合帽型加筋结构的屈曲载荷/破坏载荷和失效形式;崔勇江等[7]通过对比工程算法与有限元分析方法,进行了复合材料T型加筋板后屈曲的承载能力研究;刘文豪[8]探索了T形和工形加筋板在承载轴压载荷下的工程算法和有限元分析方法,并用试验论证了该方法的有效性;石冶金等[9]通过对J形筋条复合材料长柱加筋板的屈曲及后屈曲性能的研究,提出了一种针对长柱型加筋板极限承载能力的计算方法;晋增贵等[10]通过试验和数值仿真手段研究了短柱型复合材料结构压缩失效机理和极限承载力。Beson等[11]使用有限元模型模拟切口式铝合金加筋板的几何缺陷进行了一定的研究,并提出了一套用于有限元模拟的缺陷公式;Shen等[12]扩展了最初推导的用于预测加筋板极限压缩强度的经验公式,提出了一种自适应算法,可预测加筋板在单轴纵向压缩下的完整载荷—缩减曲线;Sun等[13]在有限元分析以及试验结果的数据基础上了,提出了一种特定的人工神经网络(artificial neural network,ANN)来预测加筋结构的屈曲载荷;Orifici等[14]采用数值方法构建了长柱型复合材料加筋壁板在轴向压缩载荷下的后屈曲分析模型,并有效预估了加筋板结构的极限强度;郑亚雄等[15]通过有限元软件ANSYS研究了长柱加筋板的后屈曲性能;王春寿等[16]应用商用有限元软件 Abaqus 研究了复合材料长柱加筋盒段在弯扭载荷作用下的屈曲和后屈曲力学性能。

从上述学者的研究内容可以看出,针对轴压情况下加筋板极限承载能力的研究大多集中在长细比大于20的中长柱或者长柱上,关于长细比小于20的短柱型加筋板极限承载能力的研究文献较少,在工程实用性上,常用切割法[17]与板元法[18]这两种计算方法。在实际问题中,对于这两种方法究竟哪种方法更加准确、实用、方便,目前没有定论。现以具有双层蒙皮的钛合金短柱型帽型加筋结构为研究对象,采用工程算法、有限元仿真分析方法,并与试验结果进行数据对比研究。验证关于长细比小于20的短柱型加筋板,板元法对其极限承载能力的计算更加精确。

1 基础理论及流程介绍

加筋板结构如图1所示。在稳定性分析中,加筋结构屈曲能力的特性分析是极其重要的,通常屈曲分析的研究是采用试验与经验公式相结合的方法,但因帽型加筋板的结构较为复杂,同时采用有限元分析方法的结果作为补充对比。针对以上方法的应用,需要掌握相关屈曲理论。

图1 试验件外形

1.1 基础屈曲理论

结构的屈曲可分为整体屈曲、局部屈曲、扭转屈曲和弯扭屈曲[19]。当加筋板只有长桁之间的蒙皮或壳发生屈曲,其他部位未见明显变形,此时的屈曲称作局部屈曲;如果长桁架和蒙皮同时变形,失去稳定性,这种屈曲模式称为全局屈曲[20]。

屈曲分析主要用于处理结构在特定载荷下的稳定性问题,阐明结构失稳的屈曲载荷,主要类型有特征值屈曲分析和非线性屈曲分析。

对结构进行线性屈曲分析时,在平衡方程中的求解过程中,不需要考虑结构在受载情况下构形的变化,即在结构初始构形上建立平衡方程为

KEu=p

(1)

式(1)中:KE为弹性刚度矩阵;u为节点位移向量;p为节点荷载向量。

对结构进行非线性屈曲分析时,需要考虑结构变形,即结构平衡方程还受到几何刚度的影响。

(KE+KG)u=p

(2)

式(2)中:KG为几何刚度矩阵。

将式(2)写成增量形式,并假定结构弹性和几何刚度保持不变,即

(KE+λGKG0)u=p

(3)

式(3)中:λG为屈曲特征值。

当Δp=0、Δu≠0(即失稳状态,在载荷不变的情况下发生位移)时,有

det(KE+λGKG0)=0

(4)

求解方程(4)即可得到结构在该荷载模式下的λG,相应地,屈曲特征值与给定荷载相乘即可得到屈曲载荷为

(KE-λGKG0)φ=0

(5)

式(5)中:φ为屈曲模态。

通过式(4)可求解得出该屈曲载荷下的φ。

但相关理论并不能直接求解得出加筋结构件的屈曲承载和屈曲模态,需要应用Abaqus有限元分析软件对其进行非线性计算,得到该类型结构件在轴压情况下的屈曲载荷和屈曲模态。

1.2 分析流程

针对钛合金帽型加筋结构件进行分析,将工程计算、有限元仿真和试验研究这3种方法相结合。具体流程如下:①介绍相关屈曲理论、非线性计算原理;②通过应用工程估算方法中的切割法和板元法,计算该类型结构件在轴向压缩载荷下的破坏载荷;③运用非线性计算原理,应用Abaqus有限元分析软件对其进行非线性数值分析,得到该结构件的极限承载能力和破坏模式;④在帽型加筋结构件的合适位置贴应变片,对其进行轴向压缩载荷下的实验研究,得到加筋结构件破坏载荷的真值;⑤通过3种方法与试验结果进行对比,对各个方法结果进行分析,得出结论。相关流程图如图2所示。

图2 分析流程图

2 工程算法及有限元仿真

2.1 工程算法

对于薄壁加筋类结构,由于筋条和薄壁之间的相互作用使得其稳定性问题变得较为复杂。目前,常用切割法与板元法这两种计算方法。

2.1.1 切割法

切割法是将构件沿变形处切开,精确测量切割面厚度,利用材料弹性模量等相关条件进行计算,得到结构件的压损应力。切割法针对不同类型的剖面,压损应力的计算公式不同。

根据飞机设计手册[21]﹐对T形、十字形和H形等对称的剖面长桁[22]的计算公式为

(6)

式(6)中:σf为剖面的压损应力;σ0.2为材料的压缩屈服极限;δ为板元件厚度;A为剖面面积;E为弹性模量;g为组成剖面凸缘的个数加上将剖面分割成一系列凸缘所需的切口个数,如图3所示。

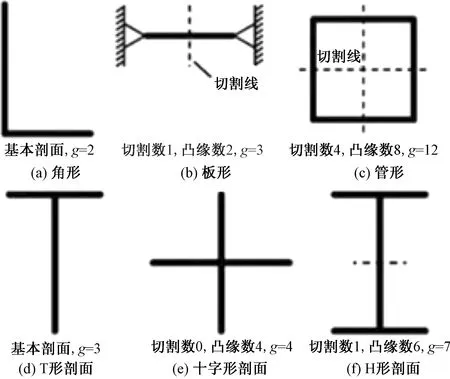
图3 切割简单元件确定g的方法

对双蒙皮帽型加筋短柱型材采用切割法,切割数为1(从中间切开),凸缘数为10,g取11,厚度t采用加权平均厚度,计算得到压损应力为586.6 MPa,承载能力为211.2 kN。

2.1.2 板元法

板元法计算压损应力是指,由一系列平板单元构成的结构可以被视为一系列具有不同程度边缘支撑的截面,即各个板元(通常为矩形板元),该结构的压损应力是各板元压损应力的加权平均值。将结构件剖面分为若干个板元,如图4所示,划分成4个一端自由,4个无自由端,然后按图5所示的挤压型材剖面板元的压损应力计算曲线分别计算各个板元的压损应力,整个截面的压损应力[3]计算公式为

图4 长桁截面自由端的确认

图5 挤压型材剖面板元的压损应力计算曲线

(7)

式(7)中:bi、δi、σft分别为第i个板元的宽度、厚度和压损应力;截止值取σ0.2;N为组成截面的板元总个数。

通过板元法计算压损应力为708.4 MPa,承载能力为255.2 kN。

2.2 短柱型钛合金帽型加筋板有限元仿真

2.2.1 模型建立

由于超塑成形工艺连接强度良好且接近于母材的强度,蒙皮和长桁连接后的焊缝界面几乎完全消失,使整个结构成为一个整体,所以本文研究中把蒙皮和长桁作为一个整体以实体单元建模。本文设计的型材参考S弯喷管后甲板的一个结构件,建立短柱型钛合金帽型加筋板有限元模型,加筋板长度为200 mm,几何参数如图6所示,材料参数如表1所示。

表1 SP700钛合金参数

图6 长桁剖面示意图

对模型进行网格划分,选择C3D8R实体单元,网格尺寸定为10 mm,结点总数为4 284,单元总数为3 060,如图7所示。

图7 网格划分

2.2.2 数值仿真

实际制造过程中产生的初始缺陷在真实结构中是不可避免的,这也使得关于结构的稳定承载能力在理论和试验值之间存在着较大的差异。由于结构的初始缺陷(初始曲率、施加的偏心载荷等),真实部件容易在低于理论值的载荷下发生屈曲。这些小偏差可能会对现实中的临界载荷产生巨大影响,所以选取非线性屈曲分析仿真。将结构的一阶模态加入结构系统中进行非线性屈曲分析可解决初始缺陷问题。

在加筋板的两个端面中心点分别创建RP-1和RP-2两个参考点,将两个参考点和各自所在的剖面通过Couping进行耦合,边界条件两端都设置为固支,通过向RP-1所在的面施加3 mm位移进行加载。有限元计算一阶屈曲模态如图8所示。

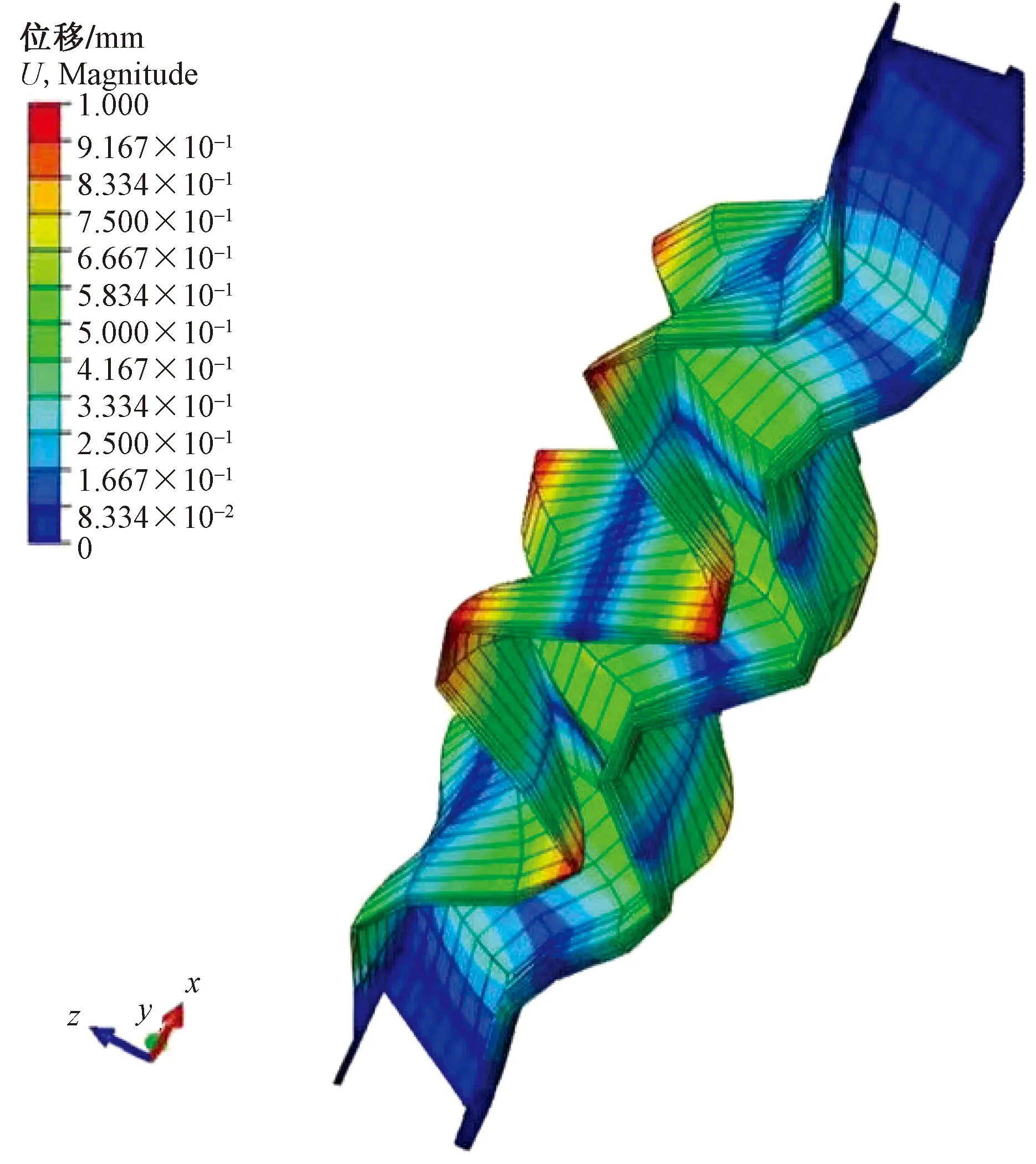
图8 一阶屈曲模态

特征值屈曲分析的结果如图8所示,magnitude表示3个方向的合位移,可见结构的屈曲模态为筋条和蒙皮的整体屈曲,2个面分别有1个凹面和1个凸起。本文研究采用“一致缺陷模态法”[23-24],模态比例因子一般取壳厚的1%,再将其乘位移场作为几何缺陷进行后屈曲分析。然后采用‘Static general’模块进行非线性分析,破坏结果如图9所示,可以看出应力主要集中在试验件的中部,并达到了极限强度1 073 MPa,试验件中部发生了较明显的变形。图10是仿真结果下的载荷位移曲线,通过仿真数据得到最大破坏载荷为252 kN,对应的位移为1.6 mm。

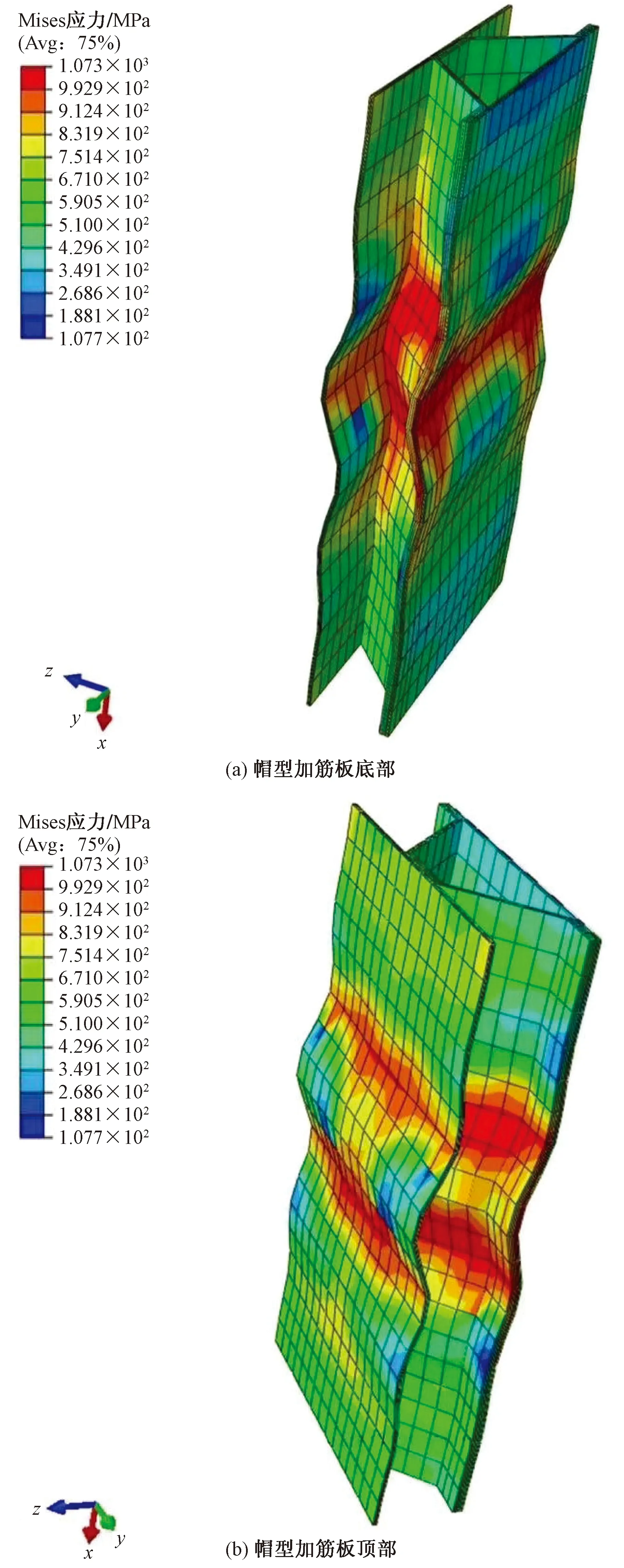
图9 极限载荷下的应力分布

图10 仿真分析下的位移载荷曲线

3 试验及对比分析

3.1 试验介绍及结果

为了验证上诉两种方法的准确性,需要用实际试验来论证。通过超塑性成形技术[21]一次性锻压成形结构件,该结构件的特点是几乎没有残余应力,符合理论分析情况。为避免试验结果的偶然性,设置3次试验。试验照片如图11所示。

试验中,通过线性增加位移载荷使得试验件发生变形,试验件破坏后如图12所示,对比仿真结果如图9所示,可以看出仿真结果下的破坏模式与真实试验的破坏模式较为接近,证明了Abaqus所进行的仿真分析具有很高的准确性,可以为此类结构件设计分析提供一定的参考价值。

试验得到的3条载荷位移曲线如图13所示,可以看出在载荷的上升阶段载荷位移曲线具有良好的线性关系,当达到最大载荷后试验件的承载能力逐渐下降。

图13 试验件载荷位移图

试验件的破坏载荷和位移汇总如表2所示,从表2中可以看出试验的平均破坏载荷为244 kN,位移为1.96 mm,证明了数值仿真和工程计算具有一定的准确性。

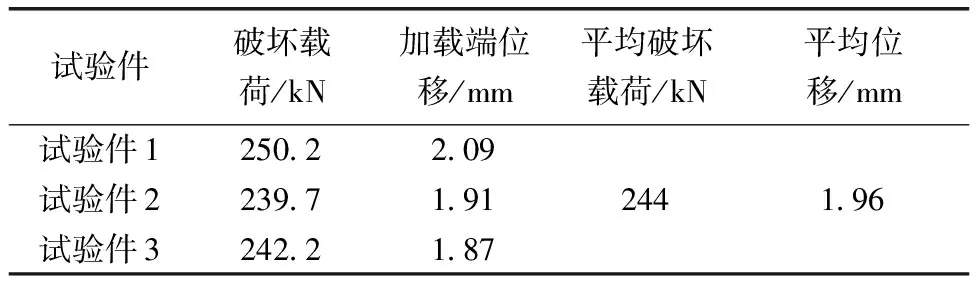
表2 试验破坏结果

3.2 结果对比分析

有限元计算和工程计算的结果对比如表3所示,可以看出切割法的误差有13.4%,相对而言,有限元仿真和板元法计算结果与真实试验值非常接近,误差分别为3.2%和4.5%。说明切割法对于这种双蒙皮帽型加筋结构破坏载荷的计算并不十分适用。

表3 试验结果与工程算法对比

(1)对于长细比小于20的短柱型加筋板,切割法、板元法与有限元方法计算精度均满足工程要求。

(2)从计算精度而言,板元法和有限元方法的计算结果与试验结果相差不大,相比于切割法精度较高。究其原因,对于帽型加筋结构件来说,剖面结构较为复杂,切割法针对T形、十字形和H形等对称的剖面的经验公式不适用于帽型加筋结构的剖面;使用板元法计算时,因为其截面完全是由规则的矩形板结构组成,所以精度高;而有限元方法则相较于工程算法考虑了初始缺陷,但由于未考虑焊缝在压缩过程中对构件的影响,因此计算结果与实际仍有一定误差。