基于交通流预测的高速公路收费站车道开闭配置

史博,宋锋,李轶群,刘猛,赵东锋,赵建东*

(1.河南交通投资集团有限公司,郑州 450000; 2.河南中原高速公路股份有限公司航空港分公司,郑州 450000;3.北京交通大学交通运输学院,北京 100044)

随着后ETC(electronic toll collection)时代的来临,中国高速公路收费站的收费模式发生了巨大的改变。首先,ETC用户规模的大幅增加导致了人工收费MTC(manual toll collection)的主体地位被电子不停车收费取代。其次,车辆的缴费方式随着各种支付手段的出现而呈现出了多元化特点。然而,现有的车道开闭配置方法无法应对高速公路时变的交通需求和多元收费模式,导致交通拥堵和车道闲置两极化现象日益严重。因此,如何针对这种新的收费模式和时变的交通需求制定合理的车道开闭配置方案是一个亟待解决的问题。

在短时交通流预测方面,基于机器学习的预测模型近年来应用广泛,主要包括K均值聚类、系统聚类、主成分分析法等无监督学习方式和支持向量机、决策树、人工神经网络等有监督学习方式[1]。其中人工神经网络在短时交通流预测中体现出了很好的适用性和有效性。宋瑞蓉等[2]为了提高交通流预测精度,将小波神经网络与果蝇优化算法相结合,解决了小波神经网络对初始参数敏感的问题。Wang等[3]基于长短时记忆神经网络(long short term memory,LSTM)和循环神经网络提出了一种基于数据驱动方法的城市道路网短期交通流预测框架,并证实其具有更高的精度和鲁棒性。Zhao等[4]针对传统机器学习在非复发性拥堵场景下的预测精度较低问题,采用LSTM进行速度预测,经评估后证明该方法具有较好的鲁棒性。

在收费车道开闭配置研究方面,方法分为两种:一种是通过构建微观仿真模型来模拟收费站在不同车道配置方案下的运营过程,再经过平均延误时间或平均排队长度等指标的评价对比后选取最终方案;另一种是利用排队论知识对收费站进行建模,确定目标函数和约束条件,选取合适算法求解得到车道配置方案。李蓉[5]针对收费站收费方式多元化,统筹考虑各方利益建立了一种收费系统资源优化配置模型,并利用遗传算法寻优求解。姬杨蓓蓓等[6]从建设成本和延误成本考虑,利用排队论知识构建了以总成本最小为目标函数的优化模型,并进行实例分析,探讨了成本与交通状态和车道配置的关系。林弼胄等[7]采用VISSIM软件构建了混合收费站仿真模型,并将仿真结果与实际观测数据进行了对比,提出了收费车道的具体配置方案。

综上所述,人工神经网络经过持续发展已经足以承担收费站的交通需求预测任务,但许多模型仍存在训练缓慢、工作量过大的问题;而现有的车道开闭配置方法主要针对的是人工收费车道,在当前的多元收费模式下亟需得到拓展。因此,现基于收费站收费数据,提出一种基于贝叶斯优化算法和LSTM的组合预测模型,用于实现收费站的交通需求预测,以及一种基于综合成本最优的车道开闭配置模型,用于确定车道开闭配置方案。

1 数据采集与预处理

所用数据采集于河北新元高速机场收费站,其中交通量数据由收费系统的通行记录获取,时间范围为2020年10月1日—12月31日;服务时间数据采用摄像法和人工统计获取,时长为2 h,为避免异常数据对研究过程的影响,对不同类型的异常数据进行预处理,其中交通量数据存在缺失值和重复值,对这部分数据直接剔除,服务时间数据存在偏大值,采用三西格玛法则进行过滤。数据经清洗后,每条交通量数据包含7个主要字段,分别为流水号、收费站名称、车道编号、时间、车型、车种和通行介质,服务时间数据包含5个主要字段,分别为车型、支付方式、实际服务时间、离去时间和服务时间。

2 基于多元收费方式的M/G/K排队模型

2.1 多元收费方式

多元收费方式是指车辆通过收费车道缴费时支付方式种类的多样化。调研中发现,目前主要的支付方式有ETC支付、现金支付、移动支付和刷卡支付4种,其中ETC支付应用于ETC专用车道,其余3种应用于MTC车道。按不同的收费方式进行交通量统计,结果显示选择ETC车道通行的用户占比已达70%,在余下选择MTC车道的30%用户中,现金支付、移动支付和刷卡支付的使用率分别为35.74%、56.38%和7.89%。

由于服务时间随着收费方式的不同存在明显差异性,其值大小与收费方式和车型密切相关,故按照车型大小和不同收费方式计算对应的服务时间均值和标准差,以ETC车型为例,结果如表1所示。

表1 ETC车型服务时间统计表

2.2 排队模型构建

高速公路收费站是一个典型的排队系统,常采用排队论展开理论研究。排队论也被称为随机服务系统理论[8],是研究排队现象的一种经典理论,其核心可分为输入过程、排队规则和服务过程三部分[9]。针对高速公路收费站,输入过程即车辆的到达过程,决定了收费站的交通需求,收费车道即提供服务的机构,所提供服务能力的大小主要由车道开启数目决定,同时也和收费方式和工作人员的操作水平有关,排队规则属于等待制,服务规则为FCFS。考虑到ETC车辆和MTC车辆分车道行驶,假设两类车辆在进入收费系统时互不干扰,对ETC收费系统和MTC收费系统分别构建排队论模型。

根据相关研究,收费站车辆到达服从泊松分布,而服务时间通常服从正态分布或负指数分布[10-11],根据本次调研得到的服务时间,采用SPSS软件分别对其进行正态性检验。经检验,各收费方式对应的服务时间基本服从正态分布,因此选择M/G/K排队模型展开研究。在M/G/K模型中,能够反映系统运营效果的重要指标分别为平均排队长度Lq、平均等待时间Wq、平均逗留时间Ws和单个服务台的服务强度ρ。

对于ETC收费系统来说,车辆在经过收费车道时不需要停车缴费,也不存在收费方式的差异,因此服务时间的均值与方差只与所统计时间段内的车型比例有关,则模型中服务时间的均值和方差计算公式为

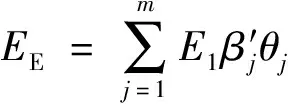
(1)

(2)

(3)

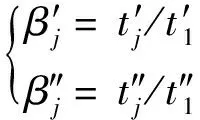
(4)

式中:EE为ETC服务时间均值,s;DE为ETC服务时间方差,s;E1为ETC小型车服务时间调研均值,s;D1为ETC小型车服务时间调研方差,s;β′j为各车型服务时间均值换算系数;β″j为各车型服务时间方差换算系数;θj为各车型比例;m为车型种类数;t′j为各车型的服务时间调研均值,s;t″j为各车型的服务时间调研方差,s。

对于MTC收费系统,由于其支付方式多元化,导致服务时间的均值和方差不仅与所统计时间段内的车型比例相关,同时也与收费方式的使用比例相关,则模型中服务时间的均值和方差计算方法为

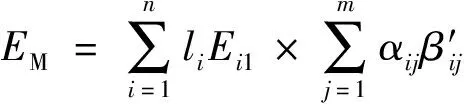
(5)

(6)

式中:

(7)

(8)

式中:EM为MTC服务时间均值,s;DM为MTC服务时间方差,s;Ei1为第i种收费方式小型车服务时间调研均值,s;Di1为第i种收费方式小型车服务时间调研方差,s;β′ij为第i种收费方式第j种车型的服务时间均值换算系数;β″ij为第i种收费方式第j种车型的服务时间方差换算系数;αij为第i种收费方式第j种车型的比例;li为收费方式占比;m为车辆类型数;n为收费方式种类数;t′ij为第i种收费方式第j种车型的服务时间调研均值,s;t″ij为第i种收费方式第j种车型的服务时间调研方差,s。

2.3 收费车道通行能力计算

服务能力的大小可以通过排队论模型中的服务时间来衡量。因此利用服务时间进行通行能力估计。即用平均服务率μ来计算单位时间内收费车道的通行能力大小。

对于ETC收费系统,收费车道通行能力仅与所统计时间段内的车型比例有关,计算公式为

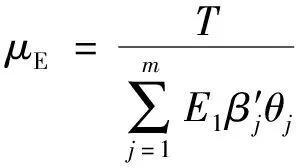
(9)

式(9)中:μE为单条ETC车道的平均服务率。

对于MTC收费系统,收费车道的通行能力除了与所统计时间段内的车型比例相关外,也与收费方式的使用比例相关,计算公式为

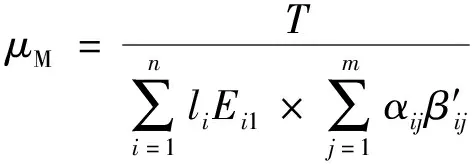
(10)

式(10)中:μM为单条MTC车道的平均服务率。

3 基于BOA-LSTM的收费站交通流预测模型

收费车道通行能力的大小反映了收费站的交通供给能力,而要实现车道配置合理化,还需要考虑收费站的交通需求。一般情况下,车道配置方案依据实际的交通量来制定,但由于交通量只能在车辆通行完毕后才能统计,此时再进行车道配置会存在严重的滞后性。为此,本文研究首先展开交通流预测。

贝叶斯优化算法[12]是一种全局优化算法,其在获得近似最优解的过程中只需要对目标函数进行较少次评估[13],从而大幅度提高模型训练的调参效率。BOA主要由概率代理模型和采集函数两部分组成[14]。概率代理模型负责计算未知目标函数概率,采集函数则用来寻找下一个变量组合。

针对交通量的时变性特点和LSTM模型的超参数调整工作量过大问题,在LSTM模型中引入BOA组合成BOA-LSTM模型实现收费站交通流预测,由上文构建的收费站M/G/K模型可知,影响收费站服务效率的关键因素是交通量、车型比例和收费方式占比,由于收费方式占比数据需结合交通调查获取,本文研究采用调研值。因此,模型预测的交通流信息中主要包括交通量和3种车型比例。模型结构如图1所示。

图1 BOA-LSTM预测模型结构图

为评价模型的预测效果,选取工作日(12月9日、12月10日和12月11日)和休息日(12月19日、12月20日和12月26日)各3 d展开预测效果验证。基于Python中的pytorch框架构建LSTM模型,并选取Adam作为梯度下降算法进行模型训练,循环迭代次数epoch设置为100,时间窗大小为20,隐藏层节点数为100;Adam优化算法中学习率为0.01。利用Hyperopt库实现贝叶斯算法优化超参数,选用树状结构Parzen估计(tree-structured parzen estimator,TPE)作为概率代理模型,预期改善函数(expected improvement,EI)为采集函数。以均方误差(mean square error,MSE)作为目标函数,对超参数中的学习率η和隐藏层神经元个数hs进行寻优。以均方根误差(root mean square error,RMSE)和平均绝对百分比误差(mean absolute percentage error,MAPE)作为预测效果的评价指标。结果如表2所示。

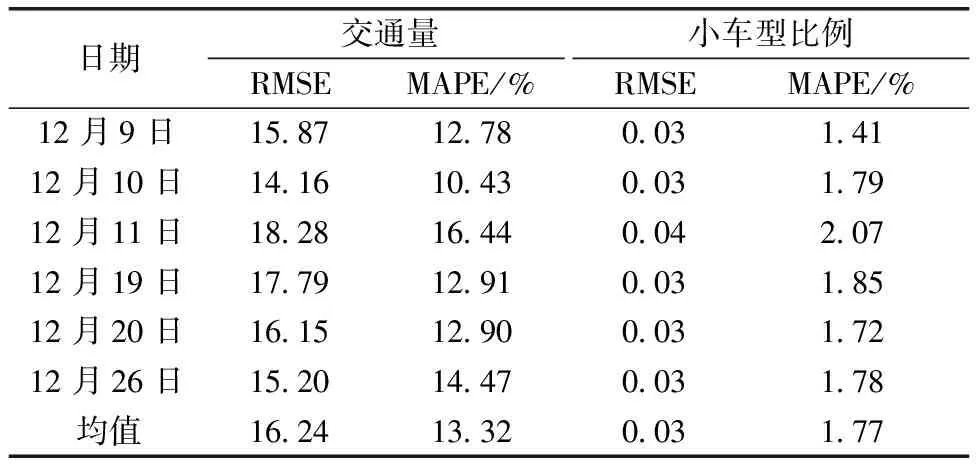
表2 BOA-LSTM模型预测效果

由于所选收费站的地理位置特殊,导致数据集中的小型车占比极大,几乎占据了总交通量的90%,而中型车和大型车占比很少,并且体现不出变化规律,因此预测过程中拟合优度出现了负数,说明效果很差,针对此类情况,将中型车和大型车的预测值采用均值替代。

4 收费车道开闭配置模型

4.1 收费站成本分析

4.1.1 运营成本

收费站运营成本Cop是收费站建成投入运营后维持正常运转需要的费用,包含工作人员工资、水电费、设备维修费等[6]。计算公式为

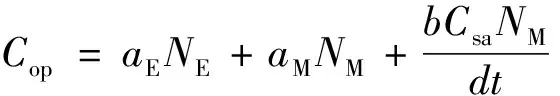
(11)

式(11)中:Cop为收费站整体运营成本,元/h;aE为一条ETC车道的运营成本,元/h;aM为一条MTC车道的运营成本,元/h;NE为收费站ETC车道的开启数;NM为收费站MTC车道的开启数;b为平均每条MTC车道安排的工作人员数;Csa为工作人员的平均月工资,元;d为每个月的工作天数,d;t为平均每天的工作时长,h。

4.1.2 用户延误时间成本

延误时间成本Cde指车辆在收费站缴费过程中,由于减速、停车和排队所造成的成本,用延误时间和时间价值来衡量。延误时间依据多元收费方式M/G/K排队模型计算得到,其中ETC车道和MTC车道的平均逗留时间分别用WsE和WsM表示。人均时间价值按式(12) 所示的收入法计算[15]。

(12)

式(12)中:A为人均时间价值,元/h;I为当地人均月收入,元。

单位时间内用户延误时间成本为

Cde=HA(λEWsE+λMWsM)

(13)

式(13)中:Cde为单位时间内的用户延误时间成本,元/h;H为车辆的平均载人数。

4.2 车道开闭配置模型构建

为综合考虑收费站管理者和出行者的利益,以运营成本和用户延误时间成本之和作为综合成本C,以综合成本最小为目标,建立目标函数为

minC=Cop+Cde

(14)

在求解最小成本的同时,所得方案必须要符合客观规律,要保证车辆的顺利通行,必须要满足以下约束条件。

(1)收费站提供的服务能力必须满足到达的交通流。为保证不会出现严重的交通阻塞,收费站必须具备足够的通行能力,即ETC车道和MTC车道的服务强度都不能超过1,且服务强度不能为负数,公式为

(15)

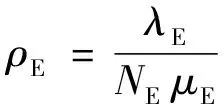
(16)

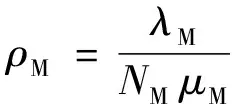
(17)

式中:ρE为ETC车道的服务强度;ρM为MTC车道的服务强度。

(2)各类型车道至少有1条在全时段开启。收费站当前可切换使用ETC和MTC两种功能的车道,且需保证两种类型的车道分别有一条以上处于全时段开启状态以防止个别车辆到来时无通道可走,即车道设置应当满足

(18)

(3)ETC和MTC车道数之和不能超过已建成的车道总数。由于混合车道兼具有ETC车道和MTC车道的功能,可以保证在收费站运营过程中实现两种类型车道功能的转换,所以两种类型的车道数不必单独设置上限,但其总和不能超过已建成的车道数,即需要满足

NE+NM≤N

(19)

式(19)中:N为已建成的车道总数。

(4)车道数均为正整数。车道开闭配置模型采用粒子群算法(particle swarm optimization,PSO)求解,整体结构如图2所示,首先将BOA-LSTM模型预测得到的收费站交通量和车型比例输入到多元收费方式M/G/K排队模型中,即依据预测得到的ETC和MTC交通量及相应的车型比例计算ETC和MTC收费车道的到达率、通行能力和车辆的平均逗留时间、服务时间均值和方差等指标,然后根据这些指标计算值和调研得到的参数确定车道开闭配置模型的各个参数,求解可得未来某一时段的车道开闭配置方案。

5 实例验证

5.1 模型求解结果

以河北新元高速机场收费站为例,获取其在2020年12月9日、12月10日以及12月11日(工作日)和12月19日、12月20日以及12月26日(休息日)的相关数据,以工作日和休息日两个场景展开实证分析,根据上述调研得到的基本信息设置模型参数,采用PSO算法求解后得到车道开闭配置方案,其中07:00—21:00的配置方案如表3所示。

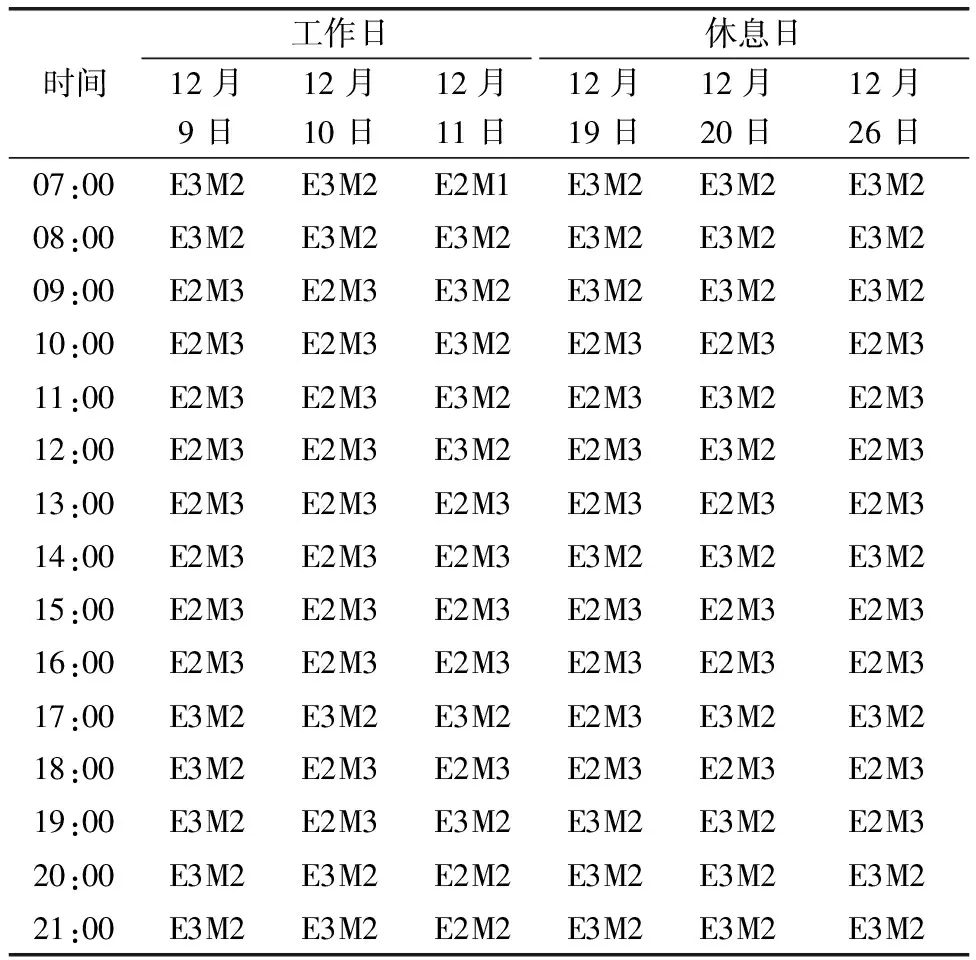
表3 车道开闭配置模型求解结果

5.2 服务水平评价

服务水平指出行者在道路上行驶时能够感受到的交通设施所提供的服务质量,用来衡量交通状态和相应的出行者感受。为衡量本文方案的实际应用效果,分别计算ETC和MTC车道的服务水平。针对MTC收费车道,采用平均排队长度Lq来划分服务水平等级,当平均排队长度在0～1 pcu时,服务水平为一级,对应交通状态为顺畅;当平均排队长度在1～4 pcu时,服务水平为二级,对应交通状态为基本顺畅;当平均排队长度在4～8 pcu时,服务水平为三级,对应交通状态为拥堵;当平均排队长度大于8 pcu时,服务水平为四级,对应交通状态为严重拥堵。针对ETC收费车道,采用服务强度ρE来衡量服务水平,当服务强度在0～0.6时,服务水平为一级,对应交通状态为顺畅;当服务强度≥0.6～0.8时,服务水平为二级,对应交通状态为基本顺畅;当服务强度在0.8～1时,服务水平为三级,对应交通状态为拥堵;当服务强度≥1时,服务水平为四级,对应交通状态为严重拥堵。根据本文模型求解方案分别计算相应的ETC车道服务强度和MTC车道的平均排队长度,工作日和休息日的结果分别如图3(a)、图3(b)和图4(a)、图4(b)所示。

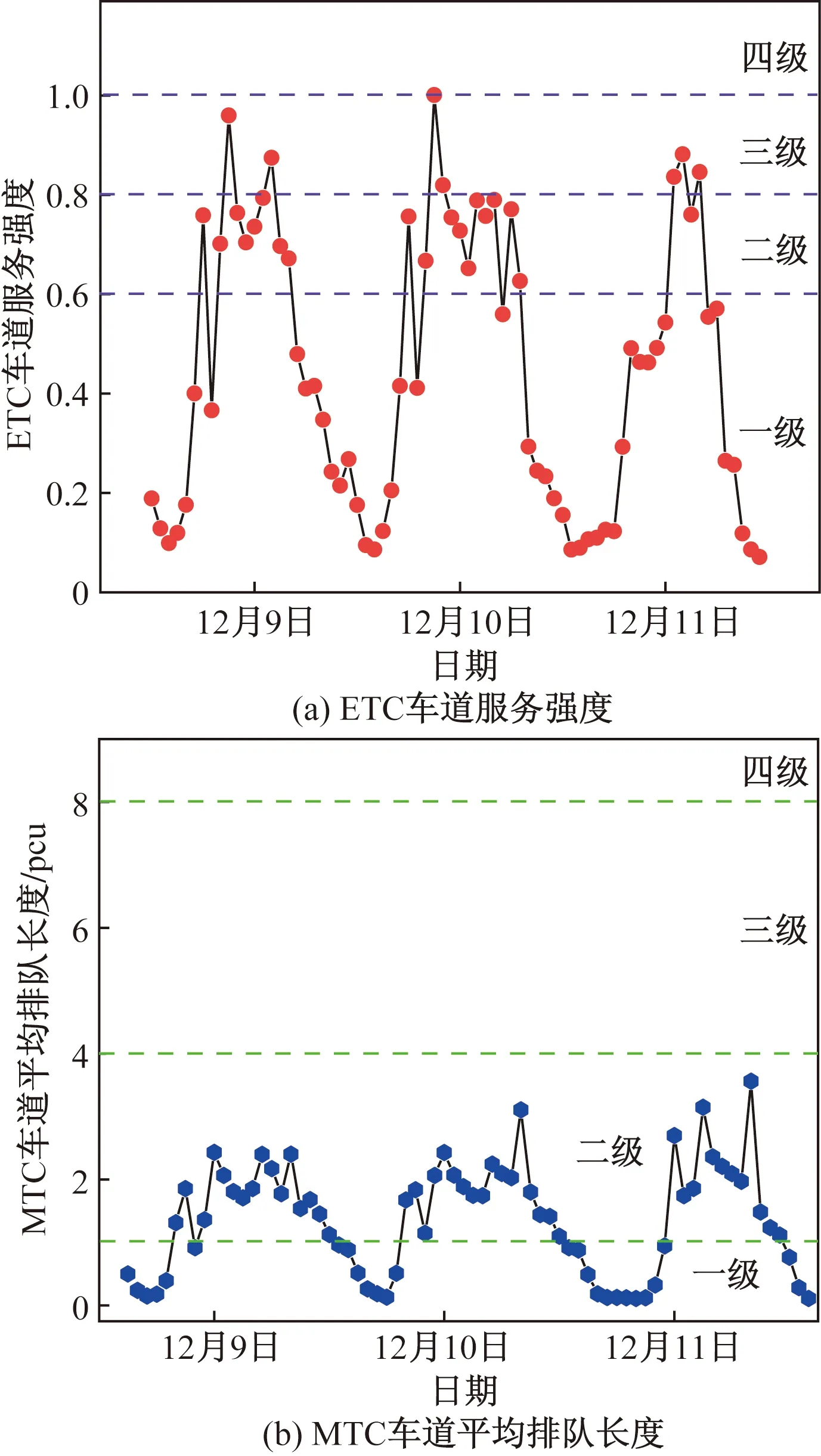
图3 工作日收费车道服务水平

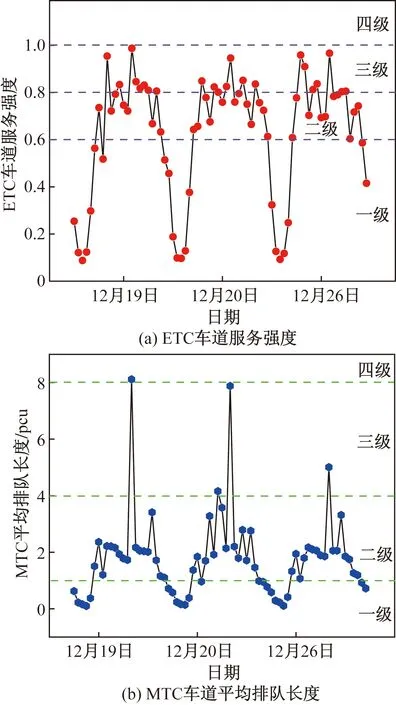
图4 休息日收费车道服务水平

按照上述服务水平划分标准依次确定其服务水平,结果表明,在工作日ETC车道处于二级以上服务水平的时间达到了90.28%,MTC车道处于二级以上服务水平的时间达到了100%;在休息日ETC车道处于二级以上服务水平的时间达到了69.44%,MTC车道处于二级以上服务水平的时间达到了94.44%。上述结果说明本文所提车道开闭配置方法能够保障车辆在收费站顺畅通行。

5.3 现状方案对比

为进一步评价上述模型得到的车道开闭配置方案,将其与现行的车道开闭配置方案进行对比分析,图5(a)和图5(b)所示分别为工作日和休息日的综合成本对比图。

图5 工作日与休息日综合成本对比

将现行方案的各项成本与本文所提方法得到的成本求差值,并计算其优化的百分比。结果表明,本文所提方法能够在一定程度上降低收费站的各项成本,相比于现状方案,工作日平均每小时的综合成本能够减少7.33元,降低了2.30%,其中,运营成本降低了1.98元,延误时间成本降低了5.36元,分别优化了2.97%和1.77%;休息日平均每小时的综合成本能够减少25.23元,降低了5.14%。其中,运营成本降低了1.24元,延误时间成本降低了23.99元,分别优化了1.89%和5.62%。

按此趋势估计,工作日每天可节约的综合成本约为175.92元,其中运营成本和时间延误成本分别为47.52元和128.4元;休息日每天可节约的综合成本约为605.52元,运营成本和时间延误成本分别为29.76元和575.76元。折算成一年来看,按照250个工作日和115个休息日计算,综合成本大约可节约113 614.8元,其中运营成本为15 302.4元,延误时间成本为98 312.4元。

6 结论

以高速公路收费站收费数据为基础,针对收费站交通需求的时变性和收费方式的多元化特点,基于深度学习方法和数学建模方法构建了BOA-LSTM组合预测模型和车道开闭配置模型,并开展了实例验证。结果表明,本文所提车道开闭配置方法能够有效解决收费站车道资源分配不均问题,具有较大的科研价值和工程意义,得出如下结论。

(1)针对ETC和MTC两种不同类型收费车道共存的现象,在M/G/K模型应用于收费站方面,提出了一种基于多元收费方式M/G/K排队模型,分别确定了ETC收费车道和MTC收费车道的服务时间均值和方差计算方法。提出了使用多元收费方式下的平均服务率计算收费车道通行能力的方法。

(2)在交通流预测方面,采用BOA对LSTM模型的学习率和隐藏层节点数进行寻优,构建了BOA-LSTM组合模型。实例验证结果显示,BOA-LSTM组合模型能够取得良好的预测效果,其中交通量和车型比例的RMSE分别为16.24和0.03,MAPE分别为13.32%和1.77%。

(3)在车道开闭配置方面,构建了以综合成本最小为目标的车道开闭配置模型,并结合高速收费站的调研情况展开了实例验证。结果表明,相比于现状方案,本文所提模型能够在保证一定服务水平的前提下,具备更高的时效性和更低的综合成本,其中工作日平均每天的综合成本能够减少175.92元,降低了2.30%,休息日平均每天的综合成本能够减少605.52元,降低了5.14%。