岩溶区铁路列车荷载对新建下穿隧道动力响应规律

2023-11-23杜碧涛刘远明陈会宇陈庆芝陈林全滕召磊

科学技术与工程 2023年30期

杜碧涛,刘远明*,陈会宇,陈庆芝,陈林全,滕召磊

(1.贵州大学土木工程学院,贵阳 550025; 2.贵州省岩土力学与工程安全重点实验室,贵阳 550025;3.贵州省交通规划勘察设计研究院股份有限公司,贵阳 550008)

随着全国各地城市轨道交通建设如火如荼地进行,隧道下穿既有铁路的工况发生得愈发频繁,例如贵阳市轨道交通3号线一期工程下穿铁路的工点就达3个之多。贵阳属于喀斯特山地城市,岩溶极其发育,因此在诸如贵阳这种岩溶地区地铁隧道施工穿越既有铁路过程中极有可能遇见拱顶溶洞,若不采取相应防控措施,地表和路基在列车长期循环振动荷载作用下,会有塌陷的风险,该事故在岩溶地区已屡见不鲜[1]。在实际工程中,遇到溶洞一般是采用注浆的方式进行填充加固,而列车动荷载对隧道及地层的动力响应在溶洞处理前后势必呈现不同的规律。

近几年,学者们关于空洞对浅埋暗挖隧道施工的影响做了不少研究[2-6]。例如,蔡义等[3-4]通过三维模型试验及FLAC3D数值模拟分析了隧道上方含空洞地层在地铁隧道施工扰动下的变形规律。赵文强[5]同样采用模型试验与数值模拟结合的手段研究了隧道开挖扰动下含空洞地层失稳机制,提出“超前地质预报+注浆防治”的控制方法并通过后期监测证实了该方法的可靠性。邢志豪等[6]依托深圳地铁16号线盾构隧道穿越岩溶溶洞工程,采用数值计算分析方法,重点研究了不同位置处溶洞注浆加固前后对地铁盾构隧道稳定性的影响作用。与此同时,关于列车动荷载对新建下穿隧道影响的研究也不少[7-10]。高玄涛[11]与龚伦等[12]通过数值分析分别研究了单线与双线列车运行对下伏隧道的影响,前者发现隧道施工至交叠处时,列车动载对隧道影响最不利;后者发现当对向行驶的两列车机车的后转向架轮载同时作用于隧道正上方时,为隧道结构的最不利位置。于鹤然等[13]研究了高速列车动荷载作用下立体交叉铁路隧道位移、加速度、内力的响应规律。Xu等[14]采用模型试验和数值模拟结合的方法,揭示了高架桥列车荷载作用下,桩土复合地基与相邻隧道的动力响应特性。魏云峰等[15]通过数值模拟对列车移动荷载作用下运营隧道-加固区-地层的系统动力响应进行研究,并得出了不同列车运行速度对结构-地层系统各测点加速度、动应力和动位移的响应规律。晏启祥等[16]设计了有、无横通道的 2 种平行交叉的盾构隧道模型,研究了列车荷载作用下平行交叉盾构隧道的动力响应特征,弄清了联络横通道对两主隧道振动响应的影响机制。

可以看出,现有研究要么是关于溶洞及注浆加固后隧道在土层中开挖时的静力影响,要么是关于在无缺陷均质地层中列车动载引起的动力响应,而在隧道下穿铁路时列车动荷载作用下,拱顶存在溶洞及注浆加固对新建隧道动力响应规律影响的研究尚有欠缺。因此,现以贵阳轨道交通3号线地铁隧道下穿川黔铁路为背景,考虑最不利条件,采用列车动力计算中常用的有限元软件Midas/GTS[17-21],建模计算分析隧道与既有铁路交叠处存在隐伏溶洞时,对其处理前后,铁路列车移动荷载对下穿隧道、地表及地层的动力响应的规律,以期为岩溶地区隧道下穿既有线工程提供参考。

1 工程背景

1.1 岩溶发育概况

贵阳市轨道交通3号线一期工程沿南北向纵贯贵阳市主城区,线路全长40.86 km,根据工程勘测资料,隧道沿线所处岩层主要以白云岩和石灰岩等可溶性碳酸盐为主。据钻孔揭露,岩层常见溶隙及溶洞,全线693个钻孔中见溶洞的钻孔75个,钻孔见洞率为10.8%,溶洞直径与埋深分布如图1所示。

1.2 隧道下穿铁路段概况

地铁隧道于花果园西站—花果园东站某区段以69°斜下穿川黔铁路,该铁路为单线,属于客货共线铁路,铁路路基底距离隧道顶部竖向最小净距约10 m。该区间隧道采用上下台阶法施工,隧道断面形状为6.52 m(宽)×7.17 m(高)的马蹄形,初支采用0.26 m厚C25喷射混凝土和I18型钢钢架0.6 m/榀。整个下穿段隧道均处于风化石灰岩地层中。

2 数值模型建立

2.1 基础三维模型

由于该区间隧道下穿段处埋深为10 m,从图1的溶洞分布图可以看出,埋深10 m以下溶洞有18个,占24%,且其中洞径最大的为5 m。基于该实际工程背景,考虑最不利条件,建立隧道施工至与铁路交叠处时,拱顶无溶洞、有直径为5 m的溶洞和溶洞注浆加固3种工况的数值模型(溶洞位于拱顶与地表正中间),计算分析列车驶过时3种工况的动力响应规律。注浆加固材料采用水泥砂浆,同时考虑浆液的扩散效应,将注浆加固区域保守地划分为厚度均为0.5 m的2部分,3种计算工况详情如图2所示。

图2 3种不同计算工况

在岩溶地区,地层情况多为上部覆盖较薄的土层,下部为可溶性风化岩层,为使该研究成果对不同工程也具有广泛的借鉴参考价值,地基简化采用岩溶区地质条件较差的强风化石灰岩。参照实际工程资料与相关规范[22],最终确定模型材料力学参数如表1所示。其中,轨枕与初期支护采用弹性本构模型,分别用实体与板单元模拟;其余各结构层次材料强度准则均采用各向同性的摩尔库伦本构模型,用实体单元模拟。

表1 模型材料参数

基于圣维南原理,取三维计算模型尺寸为:70 m(长)×50 m(宽)×50 m(高);铁路路基相关几何尺寸参照规范[22]取值:轨枕厚度为0.15 m,间距0.6 m;道砟厚度取0.3 m;基床表层与底层厚度分别为0.6 m、1.9 m。建立基础三维模型如图3所示。

2.2 特征值分析

在进行动力计算之前,需要对结构进行特征值分析获得质量参与率最高的两个模态周期,进而计算出结构的阻尼系数。根据式(1)和式(2)计算特征值分析的弹簧边界值[23]。

竖向地基反力系数为

kv=kv0(Bv/30)-3/4

(1)

水平地基反力系数为

kh=kh0(Bh/30)-3/4

(2)

表2 3种工况主振型周期

2.3 动力计算模型

2.3.1 列车荷载模拟

在实际工程中,由于列车营运场地环境的复杂性,通过现场实测获得列车动力荷载较为困难;因此,绝大多数研究对于动荷载的模拟都是采用国内外学者们根据现场试验总结出的一些经验分析方法。其中应用范围最广的是梁波等[24]提出的与高、中、低频相应的,反映不平顺、附加动荷和轨面波形磨耗效应的激励力来模拟轮轨之间的相互作用力;后经充分考虑列车轮对力在线路上的移动,叠加组合与钢轨、轨枕的分散传递因素,得到了作用在轨枕上用于模拟高速列车振动荷载的激振力函数[25]为

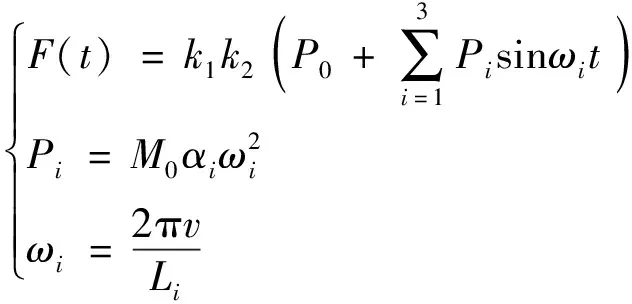
(3)

式(3)中:k1为相邻轮轨力叠加系数;k2为钢轨分散系数;P0为车轮静载;i=1,2,3,分别对应低、中、高频3种情况;Pi为振动荷载;M0为列车簧下质量;αi为轨道的几何不平顺矢高;ωi为不平顺振动波长的角频率;v为列车速度;Li为轨道不平顺波长;t为时间。

列车行驶速度越大,列车荷载对邻近建筑的动力响应也越大;因此,采用客货共线铁路最高设计时速v=200 km/h;k1、k2分别取1.6、0.8;取单轮静载P0=80 kN,簧下质量M0=950 kg,低、中、高频对应的典型不平顺波长和矢高采用英国铁路轨道不平顺功率谱:L1=10 m,a1=3.5 mm,L2=2 m,a2=0.4 mm,L3=0.5 m,a3=0.08 mm;结合式(3)计算得到列车竖向荷载时程曲线如图4所示。

图4 激振力时程曲线

2.3.2 列车荷载施加方式

列车动力荷载确定后,采用定点竖向加载的方式将荷载以固定的时间间隔依次施加在轨枕上,以模拟列车行驶过程,如图5所示。本次模拟取列车长度为130 m,而列车时速是55.56 m/s,因此列车驶过一个轨枕的时间约为2.3 s(激振力作用时长);轨枕间距为0.6 m,故激振力施加于相邻两轨枕的间隔时间为0.010 8 s;该模型路基的长度为73.2 m,所以列车从进入到完全驶出模型边界需要3.7 s。因此进行时程分析时,设置动力计算时间为4 s。为保证计算精度,隐式积分的时间步长不能大于模态分析中最高阶振型周期的1/10,因此在此计算模型中取积分步长Δt=0.01 s。

图5 列车移动荷载布置

2.3.3 动力边界条件

在进行动力理论或数值分析时,计算模型都是用有限区域代替无限区域。因此,为了合理地解决动力波在边界上的反射问题,模型x、y方向设置黏性局部人工边界,底部采用固定边界。定义黏性边界需要采用Lysmer等[26]提出的公式计算各结构材料的阻尼值。

P波阻尼系数为

(4)

S波阻尼系数为

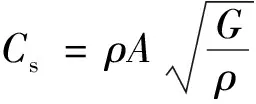
(5)

3 动力计算结果分析

3.1 分析内容与监测点布置

主要研究了在列车移动荷载作用下,交叠处隧道拱顶无溶洞、有溶洞及注浆加固3种工况下隧道结构的竖向动位移和最大主应力响应规律,地表的竖向动位移响应规律以及地层的动位移、动应力衰减规律。对研究目标的监测点布置如图6所示,地表沿路基垂直方向布置4个测点,为了便于研究分析,使测点间距与溶洞直径相近,同时要适应网格尺寸,因此取4个监测点距离隧道与路基中线交叉处分别为0.00、4.11、8.22、12.73 m。

3.2 隧道动位移响应分析

根据已有学者的研究,隧道施工至交叠处时,列车动载对隧道影响最不利[11]。因此当隧道开挖至交叠处时,在拱顶上方无溶洞、有溶洞与溶洞注浆加固3种工况模型中,分别施加激振力时程荷载模拟计算列车从驶入到驶出的完整过程,提取得到隧道拱顶的竖向动位移时程曲线如图7所示。

图7 隧道拱顶竖向位移时程曲线

分析图7可知,无论在哪种工况下,由于地层的阻尼特性对振动波传播过程产生的滞后效应,拱顶在列车驶入模型边界后约0.3 s才有位移响应,此后位移呈波动性逐渐增大;在列车完全驶入模型的时刻,即1.3 s后位移呈平稳波动趋势;随着列车行进,在2.3 s时车尾离开驶入点,同样由于振动波传播的滞后效应,拱顶竖向动位移在2.6 s后呈波动性逐渐衰减,直至列车完全驶出模型,在4 s时基本回弹恢复至零。这与张畅飞[27]采用FLAC3D计算分析上跨隧道中列车移动荷载作用下,下穿隧道拱顶的位移时程曲线具有一致的振动规律与趋势。同时也将该曲线与Sekiya等[28]在地铁运行时采用MEMS加速度计测得的隧道加速度数据进行两次数学积分后得到的位移响应曲线进行了对比,由于两者地质情况、隧道类型和列车时速不同,所以峰值大小有所差异,但同样具有相同的振动规律,该数值模型计算结果与实际工程现场实测结果存在较高相似性,因此,本文研究对实际工程具有一定的理论指导意义和参考价值。

与此同时,列车荷载作用下隧道拱腰、拱脚和拱底竖向位移也具有与拱顶相同的振动响应规律,为了更直观深入地研究分析,现将3种工况下隧道各监测点竖向动位移峰值变化情况如图8所示。

图8 隧道监测点竖向位移峰值变化趋势

综合分析图8可得如下结果。

(1)在列车动载作用下,隧道各监测点在不同工况下竖向动位移峰值大小排序均为:溶洞注浆>无溶洞>有溶洞;前者是由于注浆体的弹性模量比周围地层更大,相对不容易发生压缩变形,故将列车的竖向荷载更多地传到了注浆体以下的地层,从而使隧道支护结构产生了更大的竖向位移;后者是由于临空溶洞对动位移进行一定程度的释放。

(2)无论何种工况,各监测点竖向动位移峰值大小排序均为:拱顶>拱腰>拱脚>拱底;同时,隧道各监测点动力响应受不同工况的影响程度也遵循该规律,溶洞的存在及对其注浆对拱顶的影响相对显著,但对拱底的影响却比较微弱;显然这都是由于振动波在地层中传播时随着深度增加而逐渐衰减的缘故。

(3)隧道最大位移峰值发生在溶洞注浆工况下的拱顶位置,为-1.41 mm,相较于无溶洞和有溶洞工况分别增大了9.3%、16.5%,但即便如此,该位移仍远未达到一般隧道拱顶沉降控制标准。

3.3 地表动位移响应分析

在3种不同工况下分别施加列车移动荷载,得到地表监测点1竖向动位移时程曲线如图9所示。

图9 地表监测点1竖向位移时程曲线

不出所料,由于振动波还未经过地层阻尼的衰减,与隧道动位移相比,地表的动位移无论是波动幅度还是峰值都明显更大;为了研究不同工况下位移振动沿地表横向衰减的规律,将地表各监测点的竖向动位移峰值变化情况如图10所示。

图10 地表监测点竖向位移峰值变化趋势

综合分析图10可得如下结果。

(1)当计算结果保留两位小数时,从图10中可以看出距离交叠处较近的地表监测点1和监测点2受溶洞的存在及对其注浆的影响相对较大,3种工况下位移峰值大小排序为:有溶洞>无溶洞>溶洞注浆,而测点3和测点4几乎不受影响;由此可知在列车荷载作用下,溶洞的存在及对其注浆对地表动力响应的影响范围大致为3.3倍洞径以内(8.22×2/5≈3.3)。

(2)地表最大位移峰值发生在有溶洞工况下的测点1位置(路基中线与隧道中线交叉处),为2.74 mm,而无溶洞和溶洞注浆工况在此监测点的位移分别减小了6.6%、21.2%;由此可见,溶洞的注浆加固可以明显改善降低列车动荷载引起的地表瞬时沉降峰值。

3.4 隧道最大主应力响应分析

由于混凝土结构的抗拉强度远小于其抗压强度,而最大主应力更接近于拉应力,故将初期支护的最大主应力响应也纳入研究范围。隧道各监测点最大主应力时程曲线如图11所示。

由图11分析可知,在列车动荷载作用下,隧道在不同工况下同一监测点处的最大主应力时程曲线都具有相同的振动规律,并且拱顶和拱底主要处于受拉振动状态(正值为拉),而拱腰和拱脚则主要处于受压振动状态。为详细分析不同工况对隧道受力状态的影响规律,将各监测点的最大主应力峰值变化情况绘于图12所示。

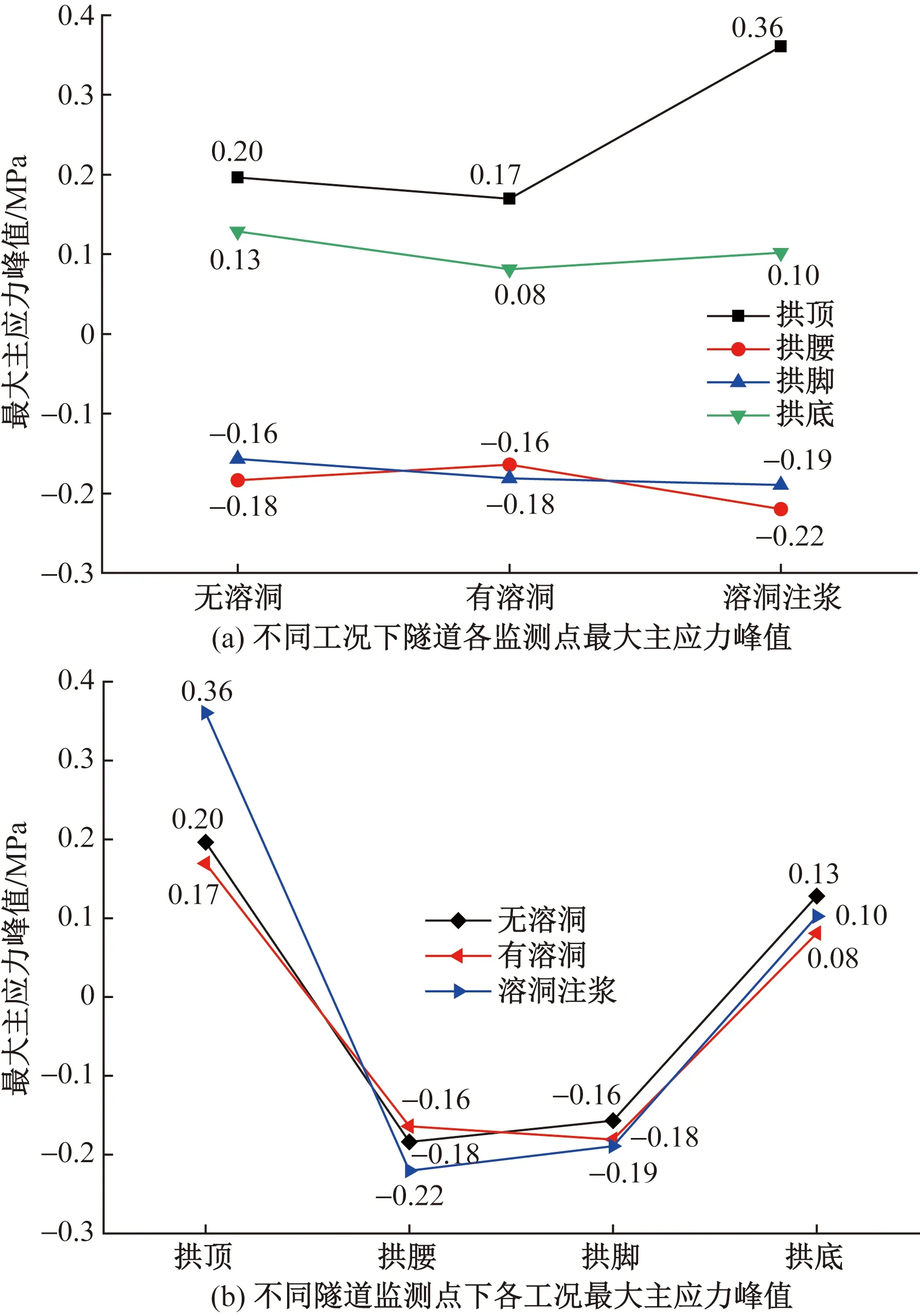
图12 隧道监测点最大主应力峰值变化趋势

综合分析图12可得如下结果。

(1)相较于无溶洞而言,溶洞的存在使振动波在地层的传播削减后,隧道拱顶、拱腰和拱底的最大主应力峰值均有所减小;而溶洞注浆则使隧道拱顶、拱腰和拱脚的最大主应力峰值均有所增大。

(2)无论何种工况下,隧道拱顶和拱底的最大主应力峰值均为正,处于不利的受拉状态,并且拱顶所受的拉应力总比拱底大;而拱腰和拱脚的最大主应力峰值均为负值,处于受压状态。

(3)溶洞注浆工况下的隧道拱顶是最不利受力点位,最大主应力峰值为-0.36 MPa,远小于C25混凝土的极限抗拉强度1.78 MPa,因此列车动载作用下隧道结构是安全的。

3.5 地层动应力衰减分析

如图13所示,列车通过时不同工况下地表监测点1的竖向应力也呈有规律的波动状态。为详细分析地层竖向应力的变化情况,将3种工况下监测点1和隧道拱顶的竖向应力峰值列于表3所示。

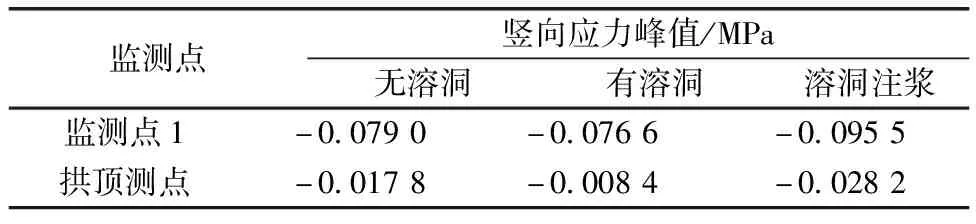
表3 地层不同监测点竖向应力峰值

图13 地表监测点1应力时程曲线

根据处于不同地层深度两监测点的应力峰值可以看出,无论哪种工况都不会改变列车动载引起的应力响应随地层深度衰减的现象。其中,衰减最明显的是有溶洞存在的情况,从-0.076 6 MPa 衰减到-0.008 4 MPa,衰减率为89.03%;无溶洞和溶洞注浆两种工况的地层应力衰减率分别是77.47%、70.47%,相对较小,这就直观解释了溶洞注浆加固后地表的动位移响应得到减小,而隧道动位移响应有所增大的现象。