压电驱动的桥式放大机构设计与优化

伍建军,周敏,章仕磊

(1.天府新能源研究院,成都 610000; 2.江西理工大学机电工程学院,赣州 341000)

柔顺机构利用柔性铰链代替装配复杂的运动关节,不仅无摩擦、灵敏度高,且一次加工成型,特别适用于精密微动领域。但柔性铰链通过形变产生运动,运动范围受限,需要位移放大机构实现相关功能[1-2]。

目前研究的放大机构有多级杠杆放大机构、差动杠杆放大机构、三角放大机构和桥式放大机构等,它们都具有各自的特点,如Li等[3]和Iqbal等[4]设计的多级杠杆放大机构虽然原理简单,在一定条件下也能实现较大的放大倍数和负载能力,但是往往需要多级杠杆才能达到需要的放大倍数,这也造成了误差累积和整体结构笨重。Fan等[5]设计的差动式杠杆放大机构虽然具有6.5倍的放大倍数和较高的固有频率,但是体积大而且分析较为复杂。Lu等[6]设计的非对称三角放大机构也存在着体积大,放大倍数不足等缺点。反观Huang等[7]和Wu等[8]设计的桥式放大机构不仅结构紧凑,且机构所得到的放大倍数和固有频率都较大。在力学研究方面,郝云锋等[9]设计了多级的嵌套菱形结构,并对其进行了分析与计算。闫洪波等[10]采用计算铰链中心点偏移量的方法来近似得出输入输出位移以计算放大倍率。林超等[11]通过能量守恒方法和弹性梁理论推导出了放大比公式和刚度计算解析式,并根据拉格朗日方程得出固有频率计算方法。Ling等[12]综合桥式和杠杆式柔顺机构,提出一种结构紧凑的新型混合三级兼容位移放大器,不仅在放大效率上有所提升,而且结构尺寸仅为57 mm×50 mm×10 mm。Chen等[13]基于伪刚体法计算输入变量与输出变量的关系,通过仿真分析验证了理论计算的正确性。

但是,传统许多针对桥式放大机构的力学研究中,没有明确菱形结构与桥式结构的区别,简单地把桥式结构简化成用连杆代替的菱形结构进行力学分析,这种不适当的简化可能导致柔顺机构的理论预测不准确。

为了说明和澄清菱形机构和桥式机构之间静态建模的混淆。现给出位移放大比的精确解析,以提高柔顺机构的输出位移的预测精度。然后,对桥式放大机构进行强度分析和动态特性分析,并通过ANSYS仿真验证理论模型的正确性。最后基于最优拉丁超立方试验设计方法获取数据,通过径向基函数(radial basis function,RBF)神经网络和多岛遗传算法(multi-island genetic algorithm,MIGA)对桥式放大机构进行多目标优化。预想通过静力学分析对桥式放大机构的放大倍数有更加精确预测,通过参数优化能进一步提高桥式放大机构的放大倍率和固有频率,扩大桥式放大机构的使用范围和响应速度。

1 结构模型

图1所示为桥式放大机构,该机构的结构对称,由8个柔性铰链、4个连梁、2个平移杆,1个输出块和1个固定块组成[14]。在两个输入端各产生Δx的输入位移,相应的在输出块位置产生2Δy的输出位移。

t为柔性铰链的厚度;t1为连接梁的厚度;d为桥式放大机构的宽度;l1和l2分别为柔性铰链和连接梁的长度;h为两个柔性铰链的间距;m1、m2、m3为连接梁的质量;PZT为压电陶瓷;Δx为压电陶瓷的驱动位移

2 静力学分析

2.1 位移放大比分析

2.1.1 欧拉-伯努利梁模型

根据如图1所示的桥式放大机构取如图2所示的一部分结构进行静力学分析,连接梁及柔性铰链的受力方程为

图2 部分结构受力图

fA=fB=fx=fPZT

(1)

2Mr=fxh

(2)

式中:fA和fB为连接梁所受的水平力;fx为柔性铰链受的拉力;Mr为柔性铰链受的力矩;fPZT为压电陶瓷产生的输入力。

根据能量守恒原理,力fPZT所做的功转化为柔性铰链的弯曲势能和拉伸变形能。

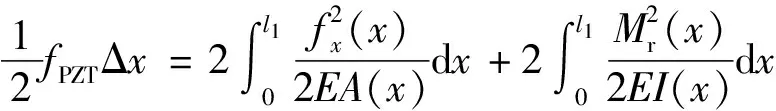
(3)

式(3)中:Δx为输入位移;Mr(x)为柔性铰链受的力矩;fx(x)为柔性铰链受的轴向力;A(x)和I(x)为柔性铰链横截面积和惯性矩;E为杨氏模量。

根据胡克定律,可以得到

fx=Kl1Δl1

(4)

式(4)中:fx为柔性铰链所受的轴向拉力;Kl1、Δl1分别为柔性铰链的拉伸刚度和轴向伸长量。

将式(4)代入式(3)并求解积分得到桥式放大机构的轴向位移为

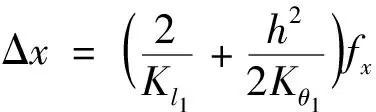
(5)

式(5)中:Kθ1为柔性铰链的转动刚度。

使用欧拉-伯努利梁理论计算变形梁的扰度作为输出位移Δy,即

(6)

式(6)中:E1为修正后的杨氏模量。

对式(6)求解积分得到输出位移为

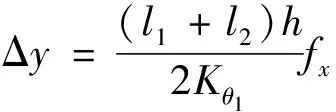
(7)

式(7)中:l1、l2分别为柔性铰链、连接梁的长度。

因此,联立式(5)和式(7)得到欧拉-伯努利梁模型的放大比为

(8)

2.1.2 考虑连接梁变形的欧拉-伯努利梁模型

考虑连接梁的变形,则输入力fPZT所做的功转化为柔性铰链和连接梁的弯曲势能与拉伸变形能,得到桥式放大机构的输入位移为

(9)

式(9)中:Kθ2和Kl2为连接梁的转动刚度和拉伸刚度。

由刚度矩阵可知Kl1、Kθ1、Kθ2和Kl2的值分别为[15]

(10)

式(10)中:d为柔性铰链的宽度;t为柔性铰链的厚度。

当d>10t时,杨氏模量E应修正为E1[15],即

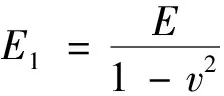
(11)

式(11)中:v为泊松比。

柔性铰链和连接梁的扰度之和作为桥式放大机构的输出位移Δy为

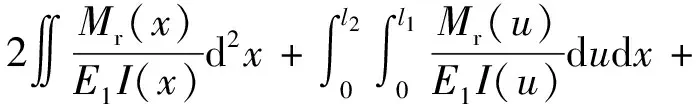
(12)

对式(12)求解积分得到输出位移为

(13)

因此,联立式(5)和式(13)得到考虑连接梁变形的欧拉-伯努利梁模型的放大比为

(14)

2.1.3 二自由度模型

Δy为输出位移;fN为连接梁所受的拉力;α为变形前杆AB与水平线的夹角;α′为变形后杆AB与水平线的夹角;Δα=α-α′图3 桥式机构简化原理图

将桥式放大机构简化为如图3所示的类似菱形的连杆结构[16],机构在输入力的作用下从实线位置变为虚线位置,桥式放大机构变形前连接梁两端的柔性铰链回转中心是点A和点B,变形后连接梁两端的柔性铰链回转中心变成了点A′和点B′,杆AB的水平夹角α在输入力作用下变为α′。

由式(1)可知fA=fB=fx,根据图3在连杆端点A处建立力矩和力方程为

fxh=2Mr=2Kθ1Δα

(15)

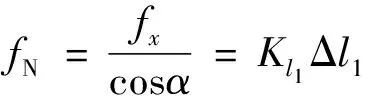
(16)

根据虚工原理,建立能量方程

fxΔx=fNΔl1+2MrΔα

(17)

联立式(15)～式(17)可得桥式放大机构的轴向位移Δx为

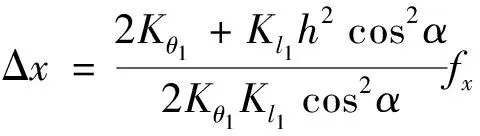
(18)

根据图3可得

ly=lABsinα

(19)

式(19)中:lAB为点A和B之间的长度。

对式(19)两边求全微分得到

dly=lABcosαdα+sinαdlAB

(20)

用微小增量代替微分得

Δy=lABcosαΔα+sinαΔlAB

(21)

由式(15)和式(16)得到Δα和Δl1,并代入式(21)得

(22)

因此,联立式(18)和式(22)得到二自由度模型的放大比为

(23)

将3种放大比模型以及单自由度模型[17]的计算结果与软件Workbench17.0的仿真结果做比较。从图4可以看出考虑连接梁变形的欧拉-伯努利梁模型的输出位移值与仿真值最接近,说明考虑连接梁变形的欧拉-伯努利梁模型具有更高的预测精度。

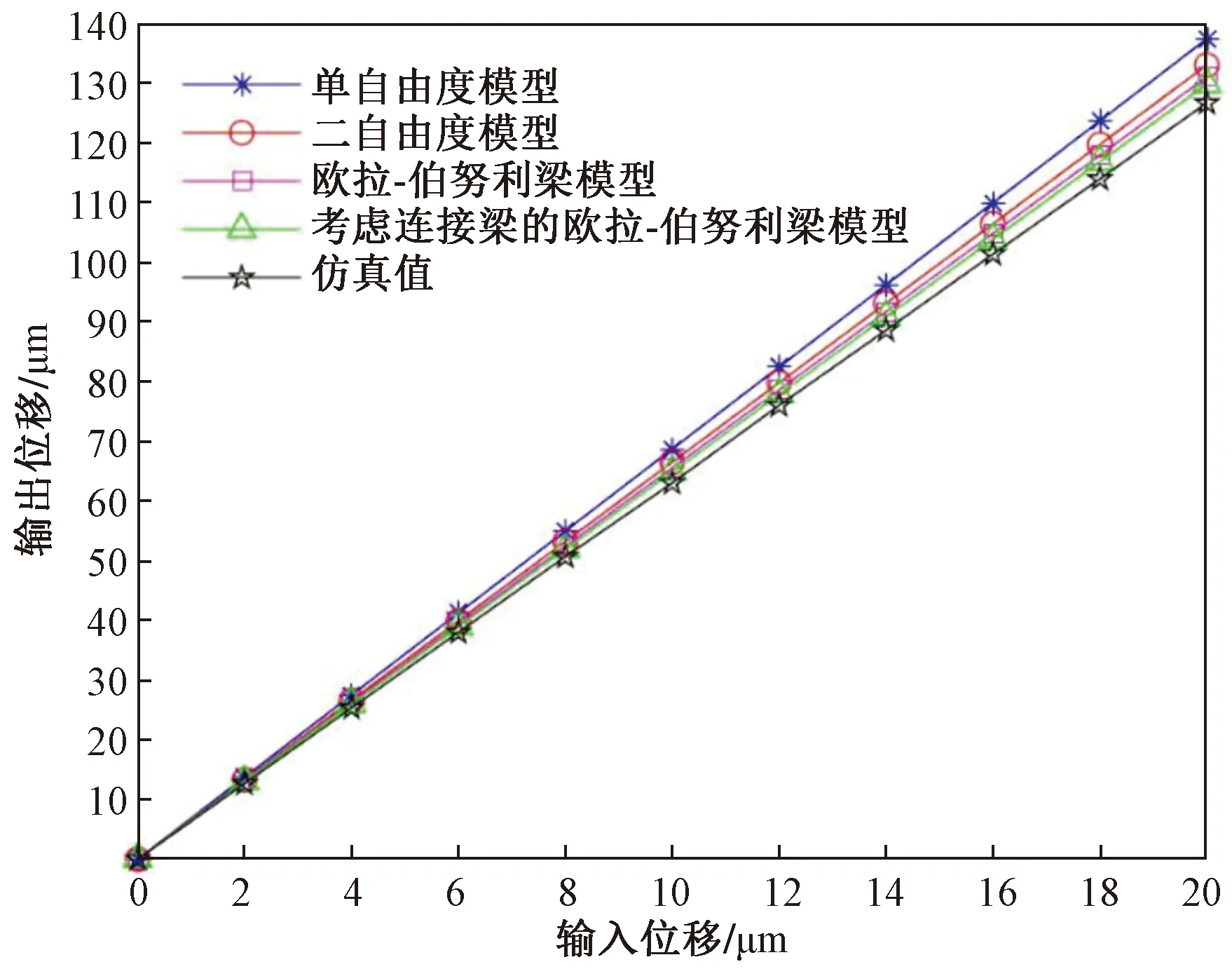
图4 各模型的放大比

2.2 应力分析

要保证材料在弹性变形范围内产生形变,需要满足最大应力小于许用应力,应力为

(24)

式(24)中:W为柔性铰链的抗弯截面系数;A为柔性铰链的截面面积。

3 动态特性分析

对桥式放大机构进行动态特性分析,因其只有y方向上一个自由度的输出,取输入位移为广义坐标q,根据图1机构模型,桥式放大机构系统动能可以表示为

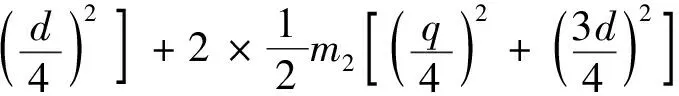
(25)

式(25)中:q为输入位移;d为输出位移,根据式(23)求出d=Ramp2q。

根据拉格朗日方程[18],桥式放大机构的等效质量M和等效刚度K分别为

(26)

桥式放大机构固有频率为

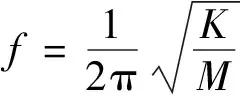
(27)

4 理论模型验证

为验证理论模型,采用ANSYS对放大机构进行有限元仿真,机构尺寸如表1所示,材料选用AL-7075铝合金,其弹性模量为71.7 GPa,泊松比为0.33,密度为2 810 kg/m3,屈服强度为503 MPa。根据放大机构的尺寸选择网格密度为0.5 mm。

将固定块固定,在x轴两端各输入10 μm的位移,得到桥式放大机构的输出位移、固有频率和应力,应力分布如图5所示,将仿真值与理论值对比,对比结果如表2所示。

表2 仿真值与理论值比较分析

图5 应力分布图

根据图5的应力分布图可知,最大应力产生在柔性铰链中间处,最大应力为40.58 MPa,远小于屈服极限,强度符合要求。从表2对比结果可以看出各性能的理论值误差均在7%以内,证明了理论模型的正确性。

5 参数优化

5.1 RBF神经网络模型的建立

由于桥式放大机构的响应与参数的关系难以用显式函数拟合,RBF神经网络模型属于非线性模型,能够通过有限的样本点建立响应与参数之间的关系模型,利用该模型预测非样本点的响应值,为桥式放大机构的结构参数设计提供优化模型。以桥式放大机构的放大倍数和固有频率作为性能指标,柔性铰链的长度l1和厚度t,连接梁的长度l2和厚度t1以及两个铰链的间距h尺寸作为参数,各参数的取值范围如表3所示,根据表3的取值范围使用最优拉丁超立方抽样确定试验点并计算对应的响应值,结果如表4所示。

表3 参数取值范围

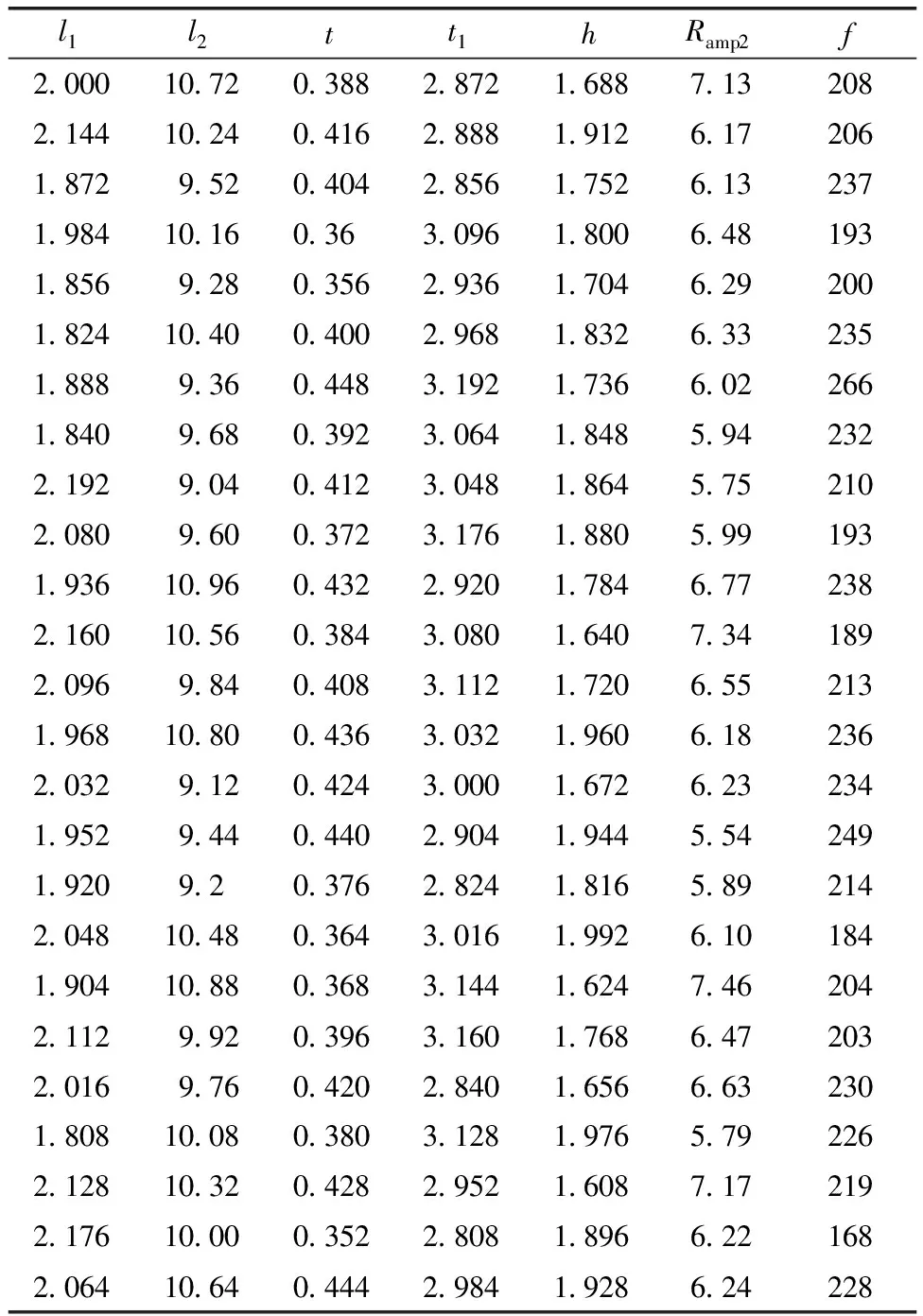
表4 试验设计数据表

(RBF)神经网络是具有3层结构的网络类型,分别为输入层、隐含层和输出层。输入层接收输入信号并传递到隐含层,输入层节点个数取决于输入变量个数,隐含层也称中间层,该层中的隐元素使用非线性变换函数将输入映射至新的空间。输出层常用线性函数作为传递函数,输出层节点个数取决于响应个数。根据本文5个参数两个响应,构建RBF神经网络模型如图6所示。

图6 RBF神经网络模型

对于RBF神经网络,使用高斯函数[19]作为径向基函数,函数形式为

(28)

式(28)中:Fi为隐含层的输出;X为n维输入向量;Ci为权值向量,与X具有相同的维数;σi为第i个隐含层节点变量,其确定了基函数半径;‖X-Ci‖为向量X-Ci的欧几里德范数;m为隐含层的节点个数。

5.2 RBF神经网络模型拟合精度检验

将表4中的数据当作训练样本,应用MATLAB自带工具箱中的newrb函数建立RBF神经网络模型。采用最优拉丁超立方抽样设计10组检验样本点,通过ANSYS仿真获得桥式放大机构这10组检验样本的放大倍数和固有频率值列于表5,通过这10组检验样本点验证模型的拟合精度。

表5 检验样本

调用MATLAB中的sim函数,输入变量是表5中的10组数据,得到RBF神经网络模型对放大倍数和固有频率的预测,预测值分别用R′amp2和f′表示,如表6所示。

表6 RBF神经网络模型预测结果

可决系数可以用来评价RBF神经网络模型的拟合精度,其计算公式[20]为

(29)

式(29)中:R2为可决系数;Xi为预测值;Yi为模拟值;n为试验次数;li为模拟值的平均值。

将表5检验样本中的响应值与表6中的响应预测值代入式(29),分别计算得到放大倍数RBF神经网络模型的可决系数R2=0.948 1和固有频率RBF神经网络模型的可决系数R2=0.941 2,R2均接近1,说明RBF神经网络模型的拟合精度较高。图7放大倍数与图8固有频率的仿真值和RBF神经网络的预测值非常接近,直观地证明了RBF神经网络模型的拟合精度较高。

图7 放大倍数模拟值与预测值对比图

图8 固有频率模拟值与预测值对比图

5.3 基于多岛遗传算法(MIGA)的多目标优化

MIGA将种群分成多个岛屿共同并行进化,相比于其他算法,它适用于参数较多的寻优。具有全局性,能避免陷入局部最优,而且求解速度快。在建立的RBF神经网络模型内进行全局寻优,各结构参数的取值范围如表3所示,MIGA的参数值设置如表7所示。寻优得到的参数值如表8所示。

表7 MIGA参数

表8 优化结构参数

将参数优化前与参数优化后的性能指标进行对比分析,对比结果如表9所示。由表9可知优化后的放大倍数7.34,相比优化前的6.33倍提高了16.0%,优化后的固有频率237 Hz,相比优化前的198 Hz提高了19.7%,优化结果符合预期,证明建立的RBF神经网络模型和采用的MIGA是准确可靠的。

表9 桥式放大机构优化前与优化后性能指标

6 结论

(1)通过对比分析可知,将变形梁的扰度作为输出位移,考虑连接梁变形的欧拉-伯努利梁模型对放大比的预测精度最高,通过仿真分析验证,放大倍数、固有频率和最大应力的理论值与仿真值的误差均在7%以内,验证了理论模型的正确性。

(2)使用最优拉丁超立方抽样确定试验点,用ANSYS仿真获得试验点的放大倍数和固有频率,采用RBF神经网络理论建立关键参数与响应之间的非线性模型,为桥式放大机构的寻优提供近似模型,最后通过多岛遗传算法寻优,结果表明放大倍数提高了16.0%,固有频率提高了19.7%,证明了所采用的优化方法具有明显效果。