渗流-流变耦合作用下深覆盖层面板堆石坝性态演化规律
2023-11-22温立峰
温立峰,李 锋,吴 莉
(1. 西安理工大学 省部共建西北旱区生态水利国家重点实验室,西安 710048;2. 中国电建集团西北勘测设计研究院有限公司,西安 710065)
0 前 言
面板堆石坝变形包括瞬时变形和时效变形。众多学者已经对覆盖层上面板堆石坝瞬时变形开展了较为深入的研究[1-2]。目前针对覆盖层上面板坝瞬时变形的研究相对较为成熟,认为流变变形是造成覆盖层面板堆石坝长期变形和防渗体失效的主要原因。蒋仲明等[3]基于流变分析理论研究了三板溪面板堆石坝的坝体变形和面板脱空现象,发现堆石料的流变效应是导致坝体后期沉降比啊逆行增加的主要因素。温立峰等[4]建立了包含56个基岩上和31个覆盖层上面板堆石坝实例的基础数据库,从统计的角度揭示了面板堆石坝流变变形与宏观影响因素的内在相关关系。赵魁芝等[5]采用双屈服面弹塑性模型对梅溪面板堆石坝的长期变形进行了分析。Pramthawee 等[6]将改进的硬化土体模型引入面板堆石坝的时效分析中,分析了流变变形对覆盖层上Nam Ngum坝应力变形的影响。已有研究一定程度上可以反映面板堆石坝的流变特性,但现有成果多依托于某个实际工程,对大坝流变特性和变形分布规律缺乏系统总结。
此外,覆盖层面板堆石坝地基和部分坝体在蓄水期处在浸润线以下,堆石体和地基存在明显的渗流-应力耦合效应。饱和区内的坝体不仅受到浮托力的作用,也受到渗流引起的渗透力的作用。渗流-应力耦合作用对深覆盖层面板堆石坝力学响应具有不可忽略的影响。陈益峰[7]等建立了混凝土面板堆石坝非线性瞬时变形与非稳态渗流耦合分析模型,分析了渗流-应力耦合作用下面板堆石坝瞬时变形规律。Wang 等[8]对地基深覆盖层开展了渗流和瞬时变形耦合分析,发现渗流-应力耦合效应对地基和防渗墙的力学特性具有重要影响。Lollino 等[9]对覆盖层上堆石坝进行了考虑堆石和地基时效变形的数值分析,讨论了固结过程对堆石坝长期变形的影响规律。Wen 等[10]采用双场迭代方法,对覆盖层上面板堆石坝开展渗流场-应力场耦合分析,发现渗流场对坝体的变形具有重要影响。当前研究主要关注渗流场对大坝瞬时变形的影响,并未在长期变形分析中考虑渗流场的影响,有必要进一步开展覆盖层面板堆石坝渗流-流变耦合分析。
本文分别采用Drucker-Prager (D-P)塑性模型和时间硬化流变模型描述堆石料和覆盖层砂砾石材料的瞬时变形和流变变形,采用Signorini 型变分不等式方法分析堆石料和覆盖层多孔介质材料的渗流过程,并在此基础上基于动量守恒原理和Kozeny-Carman方程提出覆盖层上面板堆石坝渗流-流变耦合分析方法,覆盖层上面板堆石坝开展渗流-流变耦合分析,研究渗流-流变耦合作用下覆盖层面板堆石坝的变形机制和演化过程。
1 覆盖层上面板堆石坝渗流-流变耦合分析方法
1.1 覆盖层和堆石料Drucker-Prager塑性与流变耦合模型
材料本构模型的合理性在数值计算中是准确反映堆石料力学特性的前提。当前,面板堆石坝计算中堆石料本构模型主要有非线性弹性、弹塑性和黏弹塑性模型等[11-13]。其中非线性弹性模型中的Duncan-Chang E-B模型得到广泛应用,但是E-B模型忽略了材料的剪胀性和塑性变形,且该模型无法考虑流变变形。大量实验表明,堆石料和覆盖层砂砾石材料后期剪胀作用明显增强,体积应变也由剪胀逐渐转变为收缩。有学者采用摩尔库伦弹塑性模型和基于D-P塑性的弹塑性模型描述面板堆石坝的力学响应,该类模型可以较好地反应材料的塑性变形[14]。本文采用基于Drucker-Prager的弹塑性模型描述覆盖层和堆石料的应力应变特性,采用时间硬化流变模型描述覆盖层和堆石料的时效变形。采用基于D-P塑性与时间硬化流变的耦合模型描述覆盖层地基和堆石料的力学特性。基于Drucker-Prager的弹塑性本构模型描述材料的应力应变特性,该模型采用子午线为线性单屈服面表达方式,其中屈服面函数为:
F=b-ptanφ-c
(1)
其中:
(2)
q=σ1-σ3
(3)
(4)

在恒定不变的荷载条件下,流变效应一般表现为两个阶段:第一阶段是应力重新分布,称为瞬态流变状态;第二阶段是应力状态达到稳定的阶段,称为稳态流变状态。本文研究主要考虑稳态流变阶段,采用时间硬化率流变模型描述堆石料和覆盖层的流变过程。
时间硬化流变模型(Time hardening)可以表示为如下方程:
(5)
式(5)中:εcr为等效流变应变;σcr为等效流变应力,Pa;A、n、m为流变参数,由试验拟合而得;t为时间,s。
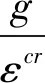
与Drucker-Prager塑性耦合的流变模型采用双曲线塑性流动势函数,它保持流变变形的方向总是由下式唯一地确定:
(6)
该耦合模型中塑性应变的方向采用相关流动法则来确定。考虑相关流动法则,即需要满足下列条件:

(7)
上述Druker-Prager屈服破坏准则和相关流动法则及时间硬化共同构成堆石料的D-P塑性和流变的耦合模型,该模型可有效地模拟覆盖层和堆石料的流变力学行为。此外,本文混凝土面板和趾板以及基岩的本构模型采用线弹性模型模拟。
1.2 渗流-流变耦合分析方法
渗流场的改变引起渗透体积力和渗透压力的改变,使得作用于坝体的荷载发生变化,影响坝体应力场和变形场。当坝体变形场发生变化时,进而改变孔隙率和渗透系数,导致渗流场发生改变。基于连续介质力学和动量守恒定律,在Biot理论框架下,变形和渗流耦合过程的控制方程可以描述如下:
(8)
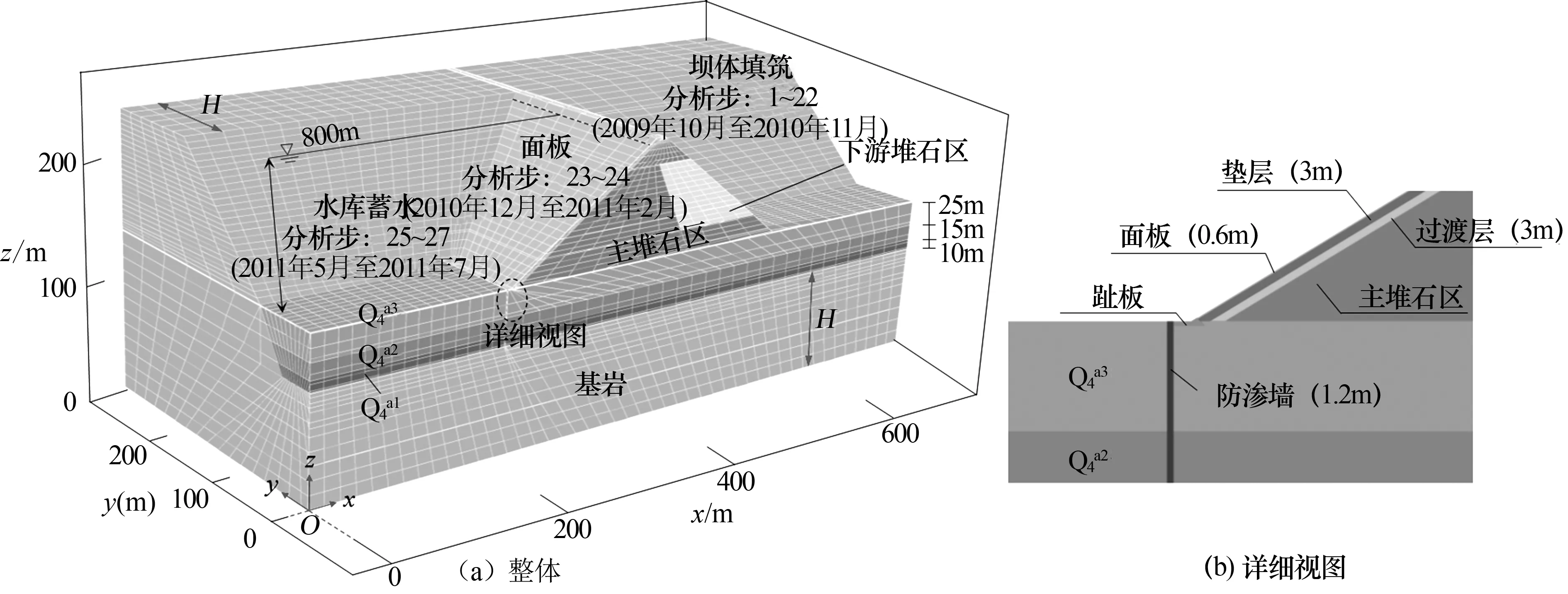
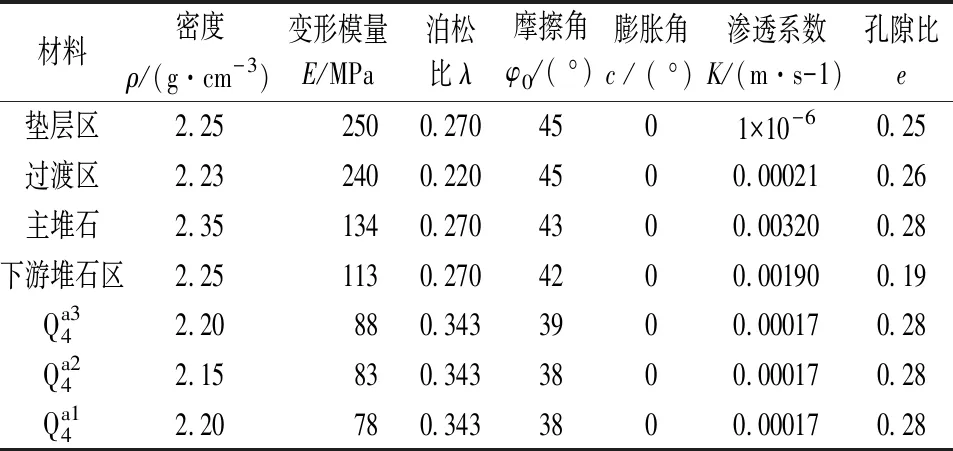
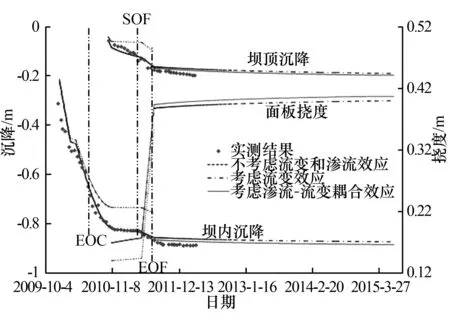
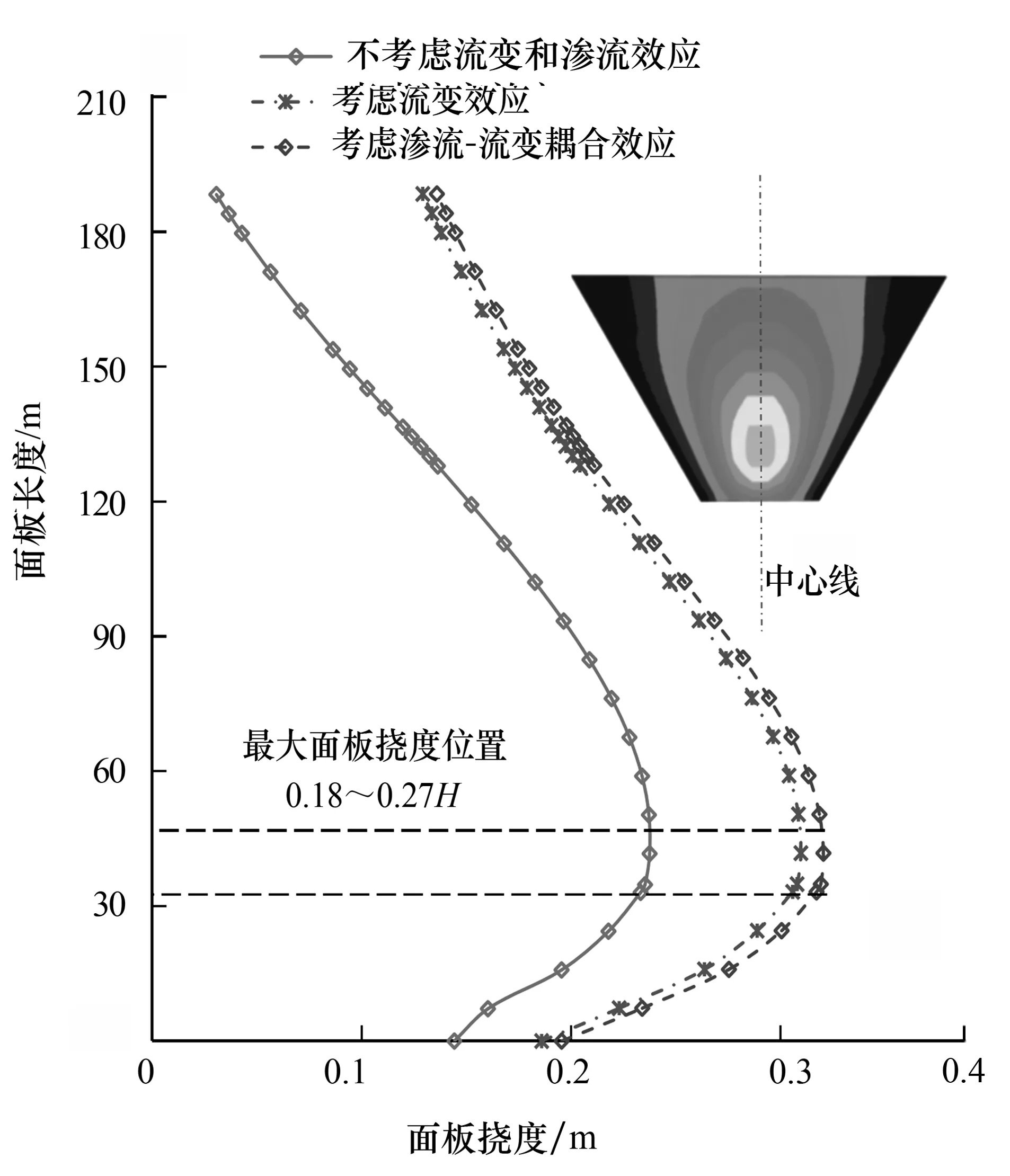
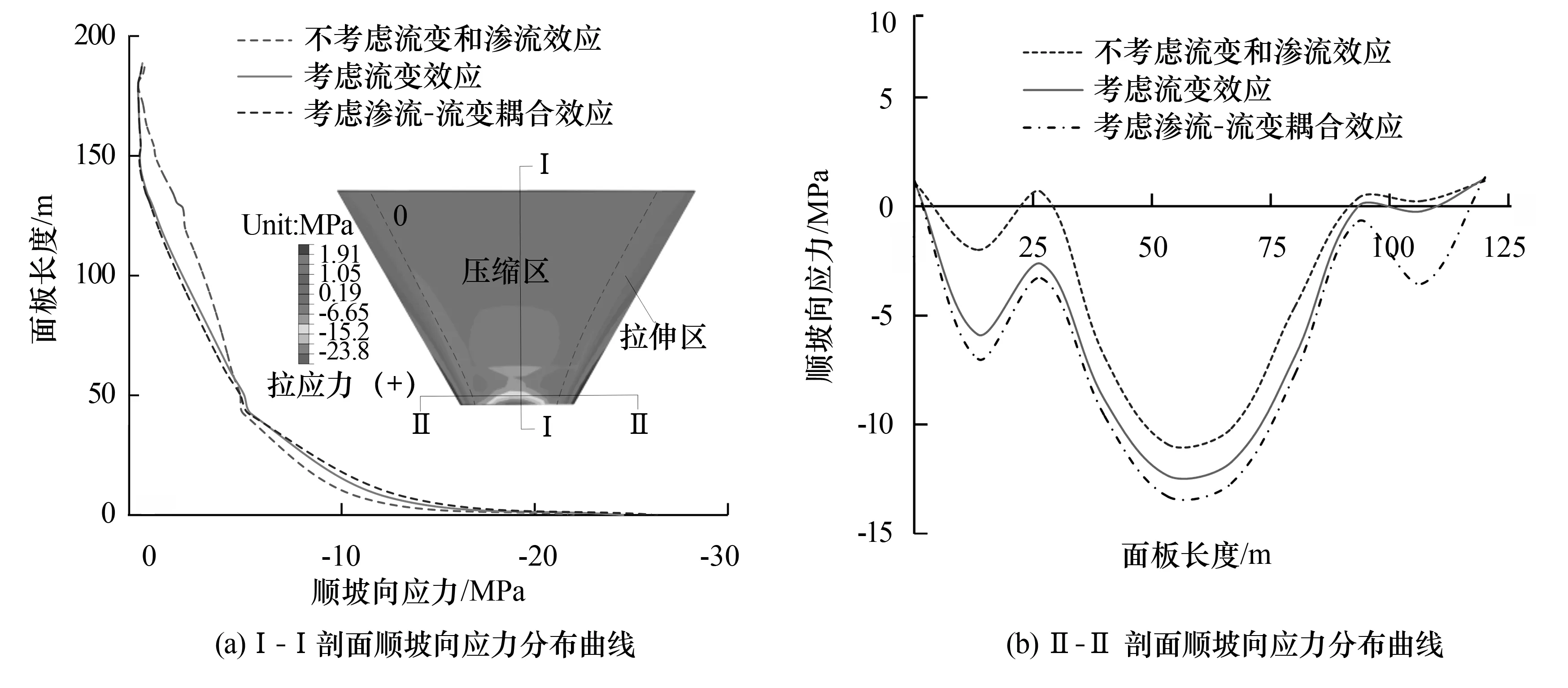
式中:其中D是切向弹性模量张量,u是位移矢量,α是Biot固结系数,δ是Kronecker三角矢量,f是体积力矢量,εv是体积应变,Sw是与水压缩性相关的存储量,t为时间,φ=z+pw/ρwg为总水头,z为垂直位置坐标,pw为孔隙水压力,H(φ-z) 是Heaviside罚函数(φ≥z时,H=1;φ 堆石料和地基变形引起孔隙率的改变将造成渗透性的变化,渗透性随应力状态的变化是模拟耦合过程的关键。在每一次迭代中,采用Kozeny-Carman方程来描述渗透性的变化并反应渗透性对孔隙率和体积变形的依赖性。小变形的假设下,孔隙率的变化与体积应变相关: (9) 式(9)中:k和k0分别为当前和初始的渗透系数;n和n0分别为当前和初始的孔隙率;εCE为流变产生的等效流变应变。 本文通过两场交叉迭代计算完成耦合分析,当前后两次迭代水头差和变形差达到容许误差(ΔH=ΔU=0.001)时,即认为双场耦合平衡。图1为渗流-流变耦合双场交叉迭代过程。通过二次开发的形式,基于ABAQUS软件开展上述耦合过程的分析。一个版块采用基于Drucker-Prager的弹塑性模型和时间硬化模型模拟堆石料和地基的瞬时和流变变形,采用中点增量法求解非线性变形过程;另一个版块采用多孔介质模拟坝体和地基的渗流行为,采用带自适应罚Heaviside 函数的抛物Signorini 型变分不等式方法消除渗流溢出点的奇异性,并实现对非稳定渗流溢出点和自由面的准确定位。每一次迭代计算时假设该次迭代渗透系数保持不变,计算流变变形。基于坝体和覆盖层地基的流变计算结果,通过式(9)计算新的渗透系数,更新渗透系数并用于下一次迭代计算。 图1 渗流-流变耦合双场交叉迭代过程 图2 苗家坝典型断面及监控设备布置 大坝数值计算模型如图3所示。模型以顺河方向为x轴,以横河方向为y轴,以沿坝体高程方向为z轴,模型计算范围从上下游坝坡坡脚算起,向上、下游方向分别延伸 200 m,左右岸及模型底部向基岩深度方向各取1倍坝高。模型真实考虑坝体结构和分区以及覆盖层基地的分层,模型总共包括40 835个八节点六面体等参单元和53 720个节点。模型上、下游侧和左右岸分别施加x和y向法向约束,模型底部施加固定约束。模型整体施加重力荷载,上游坝面施加上游水位压力水头。蓄水前,时间步长根据大坝填筑规划设置,将施工阶段分为24个阶段。蓄水后根据水位的上升速度将时间步长设置为10 d。大坝长期变形一般在4~7 a趋于稳定[15],所以该计算流变时间取4 a,时间总步长取1 460 d。 图3 三维有限元数值模型 大坝填筑材料和覆盖层地基的孔隙率和渗透系数根据工程资料和现场试验成果取得,相关参数如表1所示。初始水头分布根据水库初始渗流场计算分析得到。模型上、下游施加相应的上、下游水位,位于上、下游水位之上的大坝及坝区设置为自由溢出边界,模型底部边界以及侧面边界设置为隔水边界。进行第一次渗流-流变耦合分析计算时把初始渗流场的孔隙水压力作为流变计算的节点荷载条件施加到计算模型。 表1 弹塑性模型参数和初始渗透系数 坝体和地基渗流计算结果如图4所示。浸润线基本沿着面板与垫层之间的界面跌落,面板后坝体内的浸润线分布偏低且较为平缓。结果表明,在防渗体系的防渗作用下,覆盖层地基基本处于饱和渗流状态而坝体只有极少部位位于浸润线以下。蓄水过程中,坝基孔隙水压力随着水位的波动而变化,在水位到正常蓄水位时达到最大值,之后趋于较为稳定的状态。P2孔隙水压力大约在28 kPa,对应的压力水头为2.8 m,P6孔隙水压力大约在120 kPa,对应的压力水头为12 m,进一步说明坝体浸润线较低。两个测点计算的孔隙水压力和实测孔隙水压力吻合良好,说明本文数值模型可以较好地描述渗流行为。 大坝最大坝顶沉降、坝内沉降以及面板挠度随时间变化过程如图5所示。最终时刻面板挠度分布如图6所示。为了深入对比分析不同条件下的大坝变形计算结果,分析覆盖层上面板堆石坝变形机制,将只考虑瞬时变形、考虑瞬时和流变变形以及考虑渗流-流变耦合的变形也列在图中。大坝典型变形指标均随时间的增加而增加,施工期随着坝体的填筑大坝变形迅速增加。蓄水阶段,在水压力的作用下,大坝变形进一步增加,产生较大的变形增量。运行期在流变变形作用下大坝的变形进一步增加,只考虑瞬时变形情况下大坝变形指标数值保持不变。受覆盖层地基压缩变形的影响,大坝最大变形位置向下移动,由基岩上大坝一半坝高左右位置移动至0.3倍坝高位置。 图5 不同条件下坝体最大沉降及最大面板挠度演化规律 图6 不同条件下最终时刻面板挠度对比 只考虑瞬时变形情况下,各阶段大坝的变形均小于实测结果,计算最终时刻坝顶沉降和坝内沉降计算值较实测值分别小13 cm和10 cm。计算结果和实测结果存在较大差异。考虑流变效应情况下,上述相应的误差分别减小为2.5 cm和1.0 cm。说明流变变形是面板堆石坝的重要变形来源,此时流变引起的坝顶沉降、坝内沉降、面板挠度分别占总变形的12.20%、27.30%、11.35%。图8表明大坝流变变形主要发生在蓄水完成之前,之后流变变形速度逐渐减小。在考虑流变作用下大坝变形与实测结果仍然存在一定的误差。考虑渗流-流变耦合情况下,数值计算结果与实测结果最为吻合,坝顶沉降和坝内沉降两个变形指标数值结果与实测结果分别相差1.4 cm和0.3 cm。说明渗流效应对大坝长期变形也具有一定的影响,此时考虑渗流引起的坝顶沉降、坝内沉降、面板挠度增量分别占总变形的1.2%、3.5%、2.4%,但是渗流效应引起的流变变形增量相对于流变变形整体较小。由图8可知,渗流-流变耦合效应引起的变形增量速度呈现逐渐减小的趋势。上述结果表明,瞬时变形是大坝变形的主要来源,而流变变形是大坝长期变形的主要来源,渗流作用对大坝长期变形具有一定影响。考虑渗流-流变耦合情况下,计算所得大坝变形与实测结果误差最小,说明本文数值模型可以较为准确地预测面板堆石坝渗流-流变耦合性状。 图7为坝体和面板最大应力值随时间的变化过程曲线,图8为最终时刻面板顺坡向应力分布和典型位置应力分布对比。 图8 考虑渗流-流变耦合最终时刻面板顺坡向应力分布 由图7可知,计算结果表明应力变化过程与大坝变形变化过程基本一致,施工期快速增加,蓄水过程中也产生较大的变形增量,运行期变形增量逐渐减小。不同条件下坝体大小主应力变化和分布规律基本一致,最大应力值发生在覆盖层底部。计算最终时刻,考虑流变效应相对于只考虑瞬时变形时坝体大小主应力均有所增加,大主应力增加0.13 MPa,小主应力增加0.14 MPa。这是因为大坝流变效应引起大坝内部堆石料的应力重分配,在流变作用下坝体进一步密实,孔隙率进一步减小。考虑渗流-流变耦合作用下,坝体大小主应力相对于考虑流变效应分别增加0.50 MPa和0.16 MPa,结果表明覆盖层地基和部分坝体的渗流-应力耦合作用对坝体应力具有一定的影响。但是与坝体变形相似,渗流效应引起的应力增量较流变效应引起的变形增量总体较小。 由图8可知,面板中间主要承受压应力,在挠度变形和轴向变形的影响下,靠近两岸岸坡部位的面板出现拉应力。只考虑瞬时变形情况下面板最大压应力为2.35 MPa,最大拉应力为1.17 MPa,考虑流变作用下面板最大压应力和拉应力分别增加0.27 MPa和0.11 MPa,考虑渗流-流变耦合作用下相应的最大压应力和拉应力分别增加0.46 MPa和0.17 MPa。从计算结果可知,流变对面板拉应力产生较大的影响。在流变作用下,面板最大拉应力增加5.1%,流变变形是造成面板后期开裂破坏的重要原因,特别是对于狭窄河谷中的面板堆石坝。渗流作用引起的面板拉应力增量为2.5%,是一个值得关注的因素。 本文结合数值方法和实测资料对覆盖层上面板堆石坝开展渗流-流变耦合分析,研究渗流-流变耦合作用下覆盖层面板堆石坝力学性状,主要获得以下几点结论: (1) 本文基于动量守恒原理和Kozeny-Carman方程提出了一种覆盖层上面板堆石坝渗流-流变耦合分析方法。考虑渗流-流变耦合情况下,计算所得大坝变形与实测结果吻合较好,表明本文提出的渗流-流变耦合分析方法可以准确获得面板堆石坝渗流和变形性状。 (2) 受覆盖层地基压缩变形的影响,大坝最大变形位置向下移动,由基岩上大坝一半坝高左右位置移动至0.3倍坝高位置,同时覆盖层地基变形使面板承受较大的拉应力。 (3) 大坝流变变形主要发生在蓄水完成之前。流变变形是面板堆石坝的重要变形来源,流变引起的坝顶沉降、坝内沉降、面板挠度分别占总变形的12.20%、27.30%、11.35%,流变变形使面板最大拉应力增加5.1%。 (4) 渗流效应对大坝长期变形具有一定的影响,渗流效应引起的坝顶沉降、坝内沉降、面板挠度增量分别占总变形的1.2%、3.5%、2.4%,渗流作用引起的面板拉应力增量为2.5%,相对于流变效应引起的应力变形增量整体较小。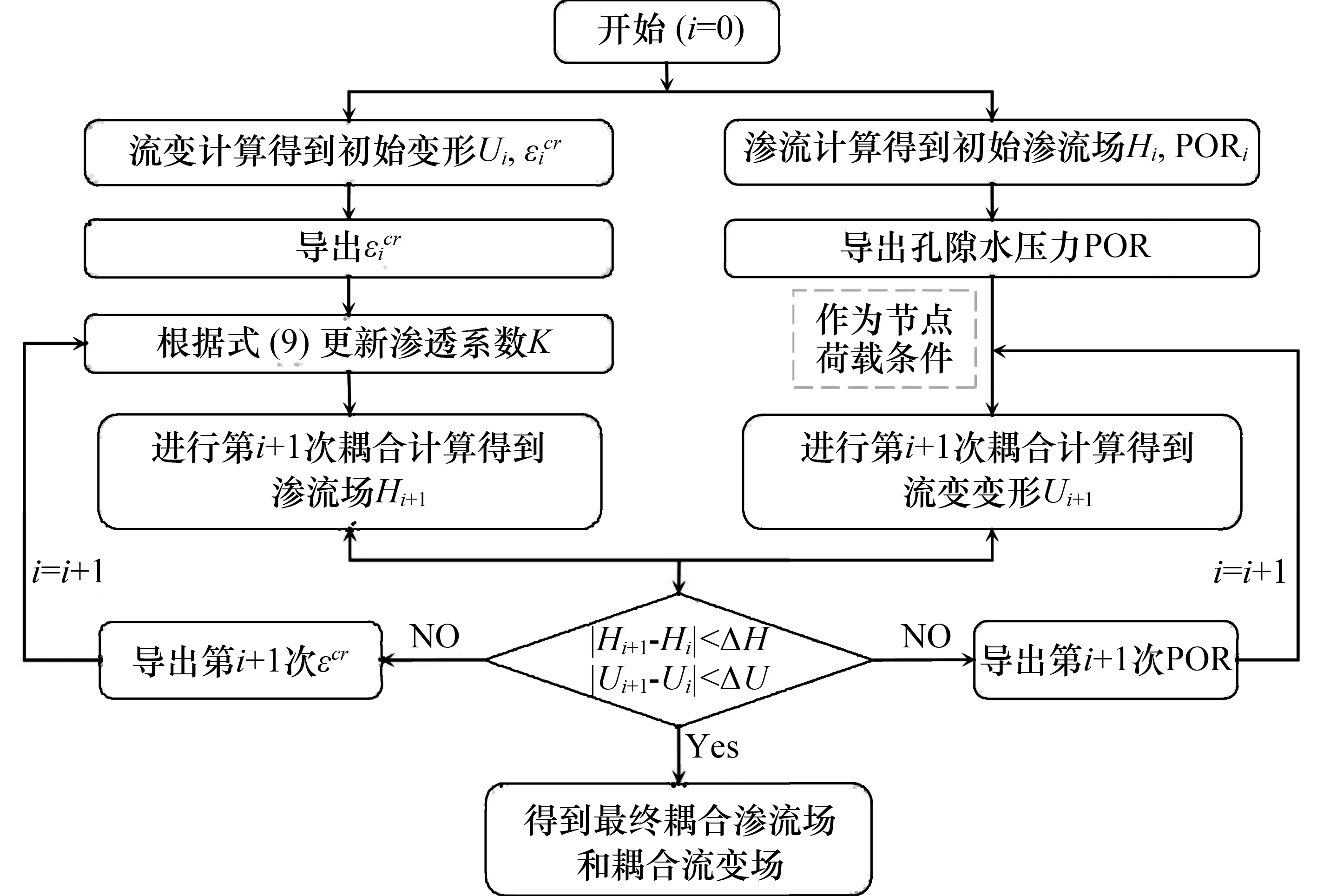
2 计算模型
2.1 工程概况
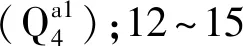
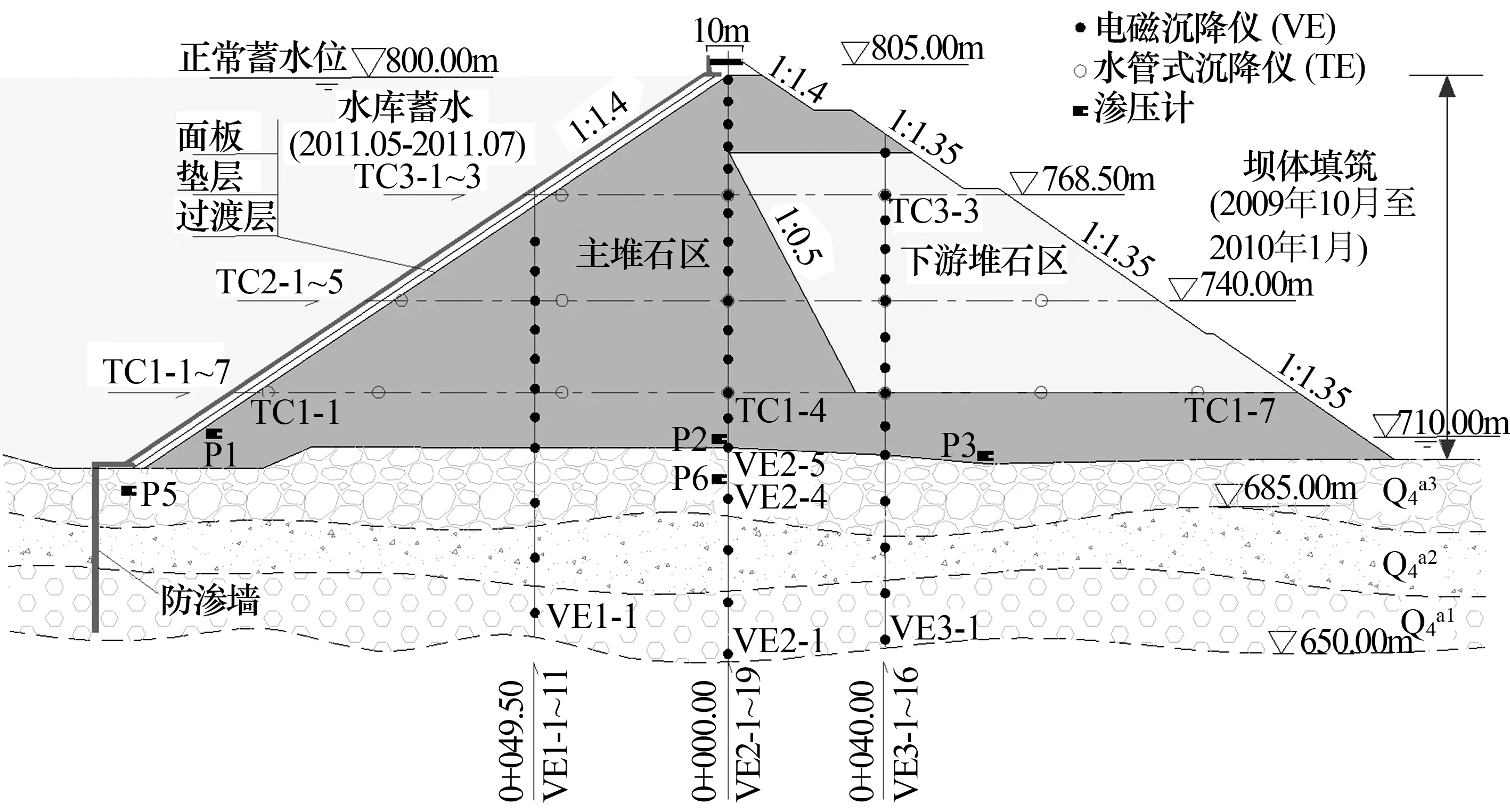
2.2 有限元模型
2.3 计算参数
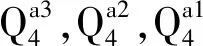
3 渗流-流变耦合分析
3.1 坝体和覆盖层地基渗流计算结果分析
3.2 变形计算结果分析
3.3 应力计算结果分析
4 结 论
