三臂凿岩台车钻臂协同钻孔防碰撞路径规划研究

吕为盛, 崔孟豪, 姬会福, 张中伟

(1. 河南工业大学机电工程学院, 河南 郑州 450001; 2. 河南农业大学烟草学院, 河南 郑州 450002)

0 引言

钻爆法[1]作为隧道、巷道掘进施工的主要方式,对不同地质条件及施工环境具有较好的适应性和通用性[2]。在公路、铁路隧道等较大型地下工程中,主要采用三臂凿岩台车作为施工设备。3个钻臂协同钻孔,施工范围大、掘进施工效率高[3]。在3个钻臂协同钻孔作业时,钻臂之间可能会发生碰撞,造成设备损坏、影响施工进度,甚至威胁到作业人员的生命安全,因此有必要对三臂凿岩台车3个钻臂的钻孔路径进行合理规划。

三臂凿岩台车钻臂可视为多关节机械臂结构,目前,机械臂路径规划方法主要有RRT[4-5]、A*[6-7]、人工势场法[8-9]、粒子群算法[10-11]等。与其他算法相比,人工势场法更易于理解,通过构建引力势场和斥力势场,使机械臂在引力和斥力的合力作用下向目标点运动,计算量相对较小,被广泛应用于机械臂和移动机器人路径规划中[12]。郝林佳等[13]将人工势场法应用于手术机器人位姿规划中,以实现手术机器人在避免碰撞的情况下实现其位姿规划; 翟丽等[14]通过改进势场环境和势场函数设计人工势场法,对无人车动态实时避障规划进行研究,通过仿真验证了该算法的可行性; 李龙等[15]提出一种接近觉的方法对UR10机械臂进行路径避障规划,将势场函数与关节空间结合,对障碍物“绕行”,基于路径规划实验验证了所用方法的有效性; 鲍久圣等[16]在传统势场法基础上引入斥力场修正因子和出逃力,并建立速度场,将其应用于井下无轨胶轮车的局部路径规划,通过仿真验证了所用方法的安全性。然而,传统人工势场法通常以笛卡尔空间作为搜索空间对机械臂进行路径规划,对于超过6个自由度的机械臂,其位姿均与每个关节的运动相关,需要实时计算其运动学逆解,计算量大、搜索效率低,且可能得到机械臂奇异位解,导致计算失败。Sepehri等[17]将RRT*和人工势场法相结合应用于机械臂路径规划,以7自由度Kinova JACO和Kinova Gen3机械臂为例,通过实验所用算法可在障碍物环境中实现机械臂免碰撞。

针对目前国内外尚未开展多钻臂协同防碰撞干涉的研究现状,本文提出一种基于改进人工势场法的三臂凿岩台车钻臂协同钻孔防碰撞路径规划方法。首先,建立三臂凿岩台车钻臂运动学模型; 其次,依据钻臂包络体模型建立钻臂碰撞干涉检测数学模型; 然后,对传统势场法势场函数进行改进,基于碰撞干涉检测结果对三臂凿岩台车钻臂进行防碰撞路径规划研究; 最后,通过仿真实验验证了所用方法的可行性。

1 三臂凿岩台车路径规划模型

三臂凿岩台车3个钻臂协同钻孔作业是提高掘进施工效率的重要手段。为防止3个钻臂协同钻孔时发生碰撞,需要对三臂凿岩台车钻臂协同钻孔进行防碰撞路径规划。在进行路径规划前,首先要判断各钻臂关节之间是否发生碰撞,基于判断结果采用改进人工势场法对钻臂进行路径规划; 而钻臂运动学是判断各钻臂关节之间是否发生碰撞的基础,因此需先得到三臂凿岩台车钻臂运动学模型。本文所研究的三臂凿岩台车的3个钻臂结构相同,如图1所示。

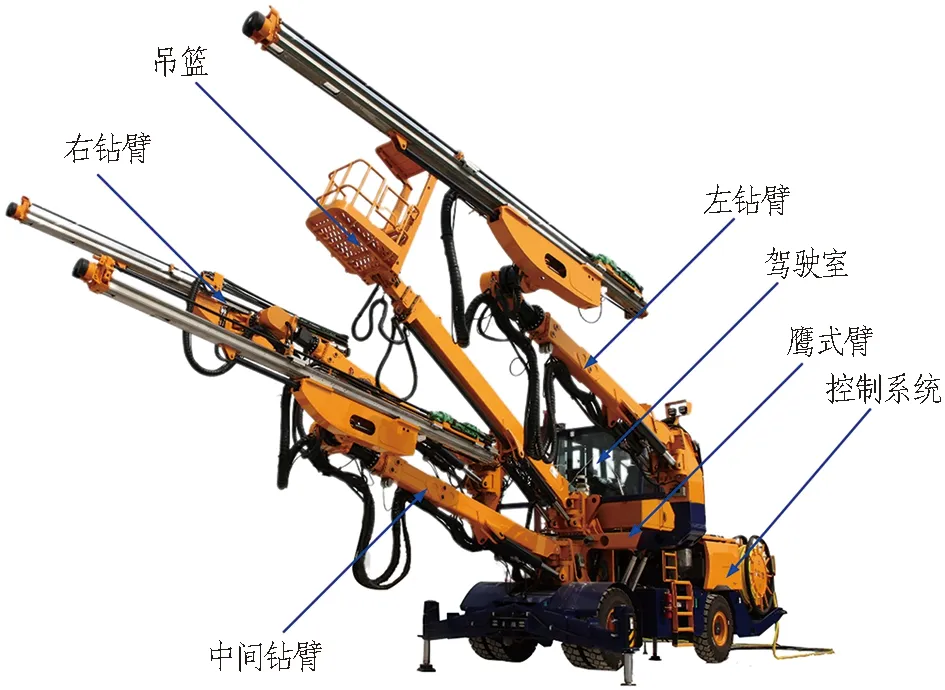
图1 三臂凿岩台车

1.1 钻臂运动学模型

1.1.1 钻臂结构

三臂凿岩台车的每个钻臂均为7自由度机械臂,包括5个转动关节和2个移动关节,钻臂整体结构安装在基座上,基座固定在车体上,采用液压方式驱动。7自由度钻臂结构模型如图2所示。

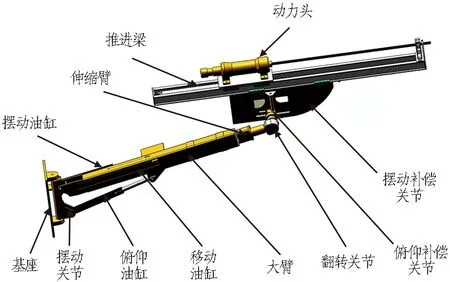
图2 7自由度钻臂结构模型

为实现钻臂有效驱动控制,首先采用改进的D-H法建立三臂凿岩台车钻臂运动学模型,获得3个钻臂结构简图和各关节坐标系,如图3所示。

(a) 左钻臂

(b) 中间钻臂

(c) 右钻臂

a、d、θ分别为连杆偏距、连杆长度、连杆转角,下同。

图3 三臂凿岩台车钻臂结构简图和各关节坐标系

Fig. 3 Boom joint coordinate system of three-boom rock drilling jumbo

1.1.2 钻臂变换矩阵

以中间钻臂基坐标系作为三臂凿岩台车钻臂全局基坐标系,左钻臂基坐标系相对于全局坐标系沿X轴负方向平移440 mm,沿Y轴正方向平移1 125 mm,沿Z轴正方向平移340 mm; 右钻臂基坐标系与左钻臂基坐标系关于全局坐标系对称。依据图3及钻臂结构参数,且本文所研究3个钻臂结构相同,以中间钻臂为例建立钻臂D-H参数表,如表1所示。

表1 中间钻臂D-H参数

基于改进D-H法建立钻臂相邻2坐标系之间的坐标变换矩阵

(1)

通过式(1)可建立钻臂末端执行器坐标系相对钻臂基座的位姿变换矩阵,如式(2)所示。

(2)

对于左右钻臂末端位姿矩阵,将左右钻臂基座坐标系相对于全局坐标系的变换矩阵左乘式(2)即可得到左右钻臂末端相对于全局坐标系的位姿变换矩阵,如式(3)所示。

(3)

1.2 钻臂碰撞干涉检测模型

1.2.1 钻臂包络模型

由于钻臂各关节结构非规则几何结构,若直接计算各钻臂的各个关节之间的距离,其计算量大、运算过程复杂。为便于计算不同钻臂各关节之间的最短距离,本文采用包络盒法对3个钻臂模型进行合理简化。钻臂包络模型如图4所示。

图4 钻臂包络模型

根据钻臂各关节结构特点,关节1—5均采用圆柱体包络盒,关节6和关节7采用长方体包络盒,其中底座固定安装在三臂凿岩台车车体上,俯仰油缸的安装底座分别在关节1和关节2上,随关节1和关节2运动,无需进行包络。基于钻臂包络模型将各钻臂之间的碰撞干涉检测转换为计算各个包络体之间最短距离的问题,从而简化计算过程,且能保证计算精度。

钻臂各关节包络体模型尺寸如表2所示。以圆柱包络体为例建立碰撞检测模型,设2个圆柱体包络盒中心线之间的最短距离为dmin,2个圆柱体包络盒的半径分别为r1、r2。为保证2个圆柱体避免碰撞,则需满足dmin>r1+r2。每个圆柱体包络盒端部圆心均为钻臂各关节节点,该节点坐标可通过钻臂正运动学计算获得,故进一步将钻臂之间碰撞干涉检测问题转换为求解空间中直线与直线及直线与点之间位置关系的问题。

1.2.2 空间中2直线之间的最短距离

设2个包络体的中心线分别为L1、L2,其中:L1的2个端点坐标分别为A1(x1,y1,z1)、A2(x2,y2,z2);L2的2个端点坐标分别为B1(x3,y3,z3)、B2(x4,y4,z4)。2条中心线上任意一点的坐标如式(4)所示。

(4)

式中: 向量A=A2-A1;B=B2-B1;α、β为系数,α∈[0,1]、β∈[0,1]。

此时L1、L2之间的最短距离问题即为求解约束函数的F(α,β)最优值问题,如式(5)所示。

F(α,β)=‖A(α)-B(β)‖2=‖(A1+αA)-(B1+βB)‖2。

(5)

求F(α,β)的极小值,令F(α,β)关于α、β偏导均为0,如式(6)所示。

(6)

由此计算出:

(7)

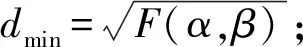
1.2.3 空间中点到直线的最短距离

与求解2直线最短距离过程类似,将点到直线的最短距离问题转换为求解约束函数的最优值问题,设空间中一点M(x,y,z),以计算点M到中心线L1的最短距离为例进行说明,其约束函数如式(8)所示。

F(α)=‖M-A(α)‖2=‖M-(A1+αA)‖2。

(8)

令F(α)关于α的偏导为0。

(9)

结合式(4)、(8)、(9),可得:

(10)

通过dmin即可判断钻臂之间是否发生碰撞。

2 钻臂防碰撞路径规划方法

为避免钻臂运动过程中存在奇异位解,导致计算失败,同时避免按照钻孔顺序运动过程中发生钻臂碰撞干涉,本文首先建立钻臂钻孔路径规划模型,其次以关节空间作为搜索钻臂下一个动作姿态的搜索空间,采用改进人工势场法对三臂凿岩台车钻臂进行防碰撞位姿调整。

2.1 钻臂钻孔路径规划模型

2.1.1 钻臂工作区域划分

根据三臂凿岩台车运动学模型,基于蒙特卡洛法计算出三臂凿岩台车工作范围。三臂凿岩台车工作空间如图5所示。

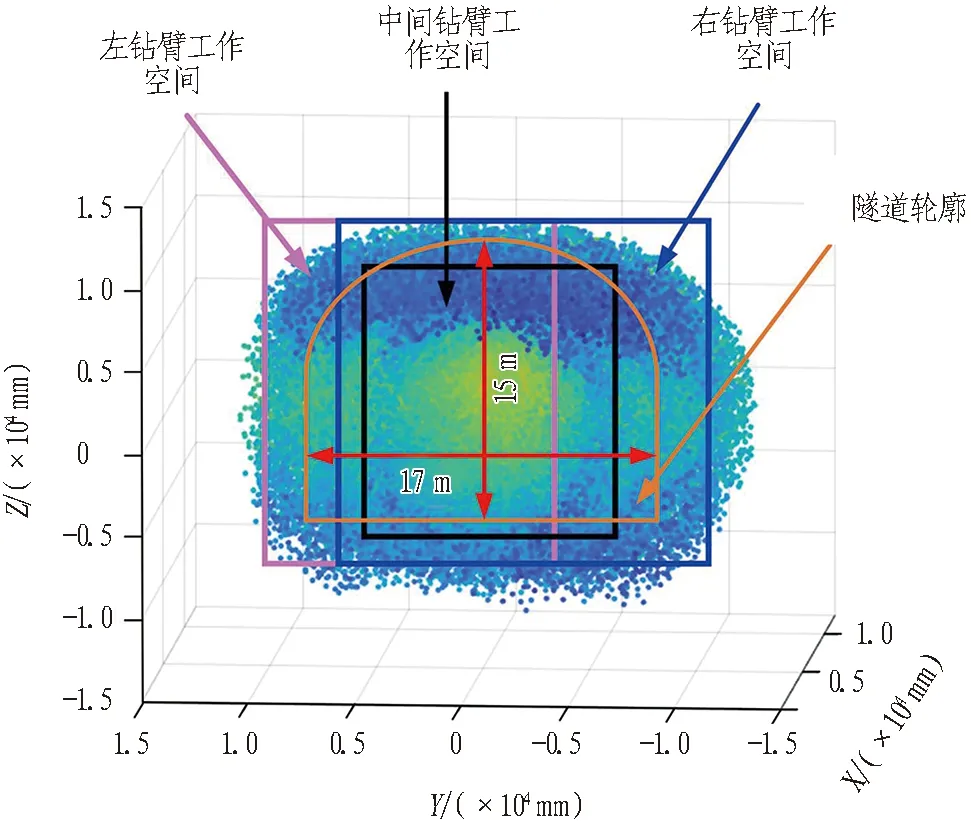
图5 三臂凿岩台车工作空间

隧道掌子面所布孔位数量为188个,依据所得3个钻臂的工作空间,对每个钻臂工作区域进行划分,并以钻臂末端行驶距离最短和各关节变量之和最小为优化目标对钻孔顺序进行优化。钻臂工作空间划分及钻孔顺序如图6所示。

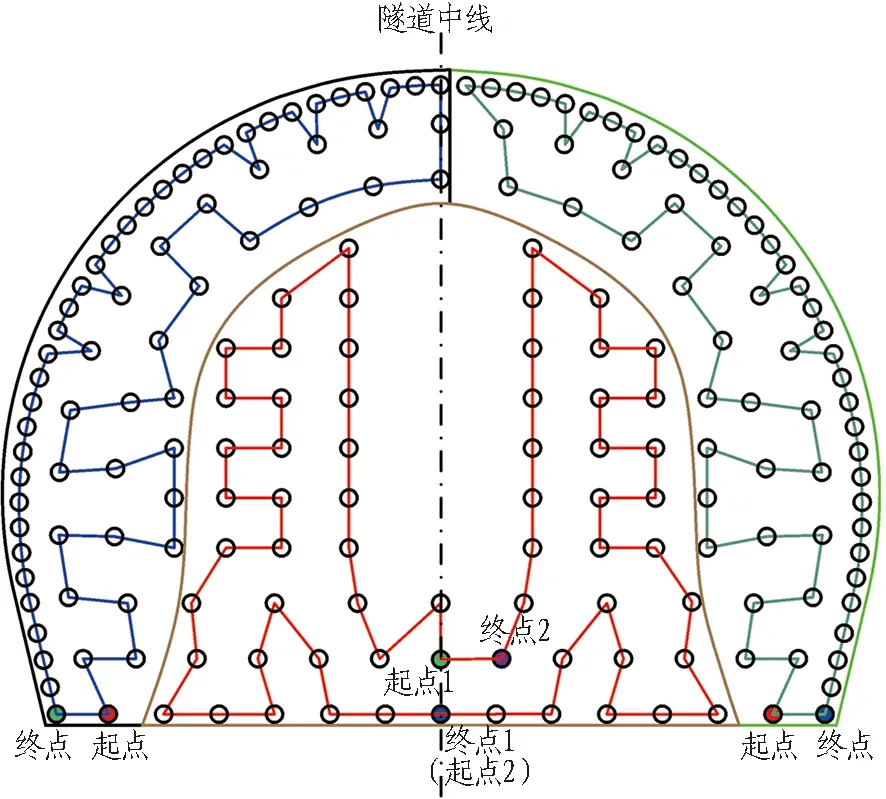
(a) 距离最短钻孔顺序

2.1.2 钻孔顺序优化

从左到右依次为左钻臂、中间钻臂、右钻臂工作区域及各钻臂优化后钻孔顺序,钻孔数分别为64、63、61,钻孔顺序优化参考文献[18],考虑节约钻孔施工能耗,分别以钻臂末端移动行驶距离最短作为和各关节变量之和最小优化目标,采用改进遗传算法对钻孔顺序进行优化,优化目标如式(11)所示。

(11)

式中:S为钻臂末端执行器移动距离;l为2空位之间的距离;n为孔位数量;R为钻臂各关节变量总和;θ为关节变量。

孔位关于隧道中线对称分布,依据所划分工作空间,每个钻臂仅在所划分工作空间内作业,由此可知钻臂之间的碰撞主要发生在中间钻臂与左右钻臂之间。图6中,在中间钻臂工作区域内,起点1为中间钻臂与左钻臂之间路径规划时中间钻臂起点,终点1既是中间钻臂与左钻臂路径规划终点,也是中间钻臂与右钻臂路径规划时的起点。

2.2 势场函数建立

2.2.1 引力势场函数

基于建立的钻臂钻孔路径模型,考虑传统势场函数仅对钻臂末端起约束作用,而钻臂作业过程中由各关节控制钻臂运动。为提高对钻臂的控制精度,使所规划的路径更加合理,将势能引入钻臂各关节,保证势场函数可以约束钻臂位姿。

基于关节空间重新建立引力势能函数:

(12)

则与其对应的引力函数为:

(13)

式中:Fatt(q)为钻臂关节的引力;Fatt为钻臂各关节引力之和。

2.2.2 斥力势场函数

传统势场中,当障碍物在目标点附近时,钻臂受到的斥力较大,导致钻臂无法到达目标点,因此对传统斥力势能函数进行重建,避免在目标点周围时所受斥力过大,新斥力函数如式(14)所示。

(14)

式中:Urep(q)为钻臂关节斥力势能;Urep为钻臂各关节斥力势能总和;λ为斥力势能因子;qobs为障碍物位置;d(qi,qobs)为钻臂关节当前位置到障碍物之间的最小距离;d(qi,qgoal)为钻臂关节当前位置到目标位置的距离;dA为障碍物的斥力势能作用范围。

由此,使钻臂远离障碍物运动时,对应的斥力函数为:

(15)

式中:Freq(q)为钻臂第i个关节所受到的斥力;Freq为钻臂所有关节所受斥力总和;NOR和NRG为2个向量,分别表示钻臂关节到障碍物的距离和钻臂关节到目标距离的单位向量,Freq1、Freq2如式(16)所示。

(16)

由上述分析在进行防碰撞路径规划时,各个钻臂所受到势能和力的总和如式(17)所示。

(17)

3 仿真实验研究

为分析基于改进人工势场法用于三臂凿岩台车防碰撞路径规划的可行性及高效性,基于图6所建立的钻孔顺序,引入改进的人工势场法进行多钻臂协同钻孔防碰撞位姿调整。由于在本文所提到的三臂凿岩车在实际工作时的钻孔深度较浅,所面临的环境与工况不复杂,一般不会出现钻臂钎转压力和推进压力陡然上升到最大值引起卡钎的情况,卡钎出现概率很低,因此本文暂不考虑因卡钎导致的钻孔时间不一致的情况。

3.1 基于距离最短钻孔顺序的路径规划

3.1.1 实验仿真

为实现三臂凿岩台车的精准路径规划,施工过程中需要先将凿岩台车放置于巷道中间,按照设定的路径进行钻孔作业,三臂起始孔位置在施工中一般均由程序设定为固定位置。因此,本文基于距离最短钻孔顺序时中间钻臂与左右钻臂之间的最短距离衡量钻臂碰撞干涉。依据图6(a)所示各个钻臂起始点分别对中间钻臂与左钻臂、中间钻臂与右钻臂进行无碰撞路径规划仿真,结果如图7和图8所示。

(a) 两钻臂初始工作姿态

(b) 中间钻臂完成钻孔任务

(c) 两钻臂完成钻孔任务

(a) 两钻臂初始工作姿态

(b) 中间钻臂完成钻孔任务

(c) 两钻臂完成钻孔任务

图7(a)、8(a)为2个钻臂开始钻孔任务时的初始状态,该姿态由三臂凿岩台车车体定位实现,在车体定位过程中,钻臂之间不会发生碰撞,故本文省去定位过程中各个钻臂之间碰撞干涉检测; 图7(b)、8(b)为中间钻臂完成其钻孔任务后2个钻臂之间的状态,中间钻臂处于停止运动状态,左右钻臂继续钻孔作业,图7(c)、8(c)为2个钻臂均完成钻孔任务后的工作状态。由图7和图8可知,2个钻臂在钻孔时完全按照所优化的钻孔顺序进行。

3.1.2 碰撞判定

进一步对钻臂简化后各关节之间距离依据从大到小进行排序,并提取2个钻臂同时钻孔时各钻臂包络盒之间最短距离,以判断两钻臂之间是否发生碰撞。钻臂之间最短距离如图9所示。

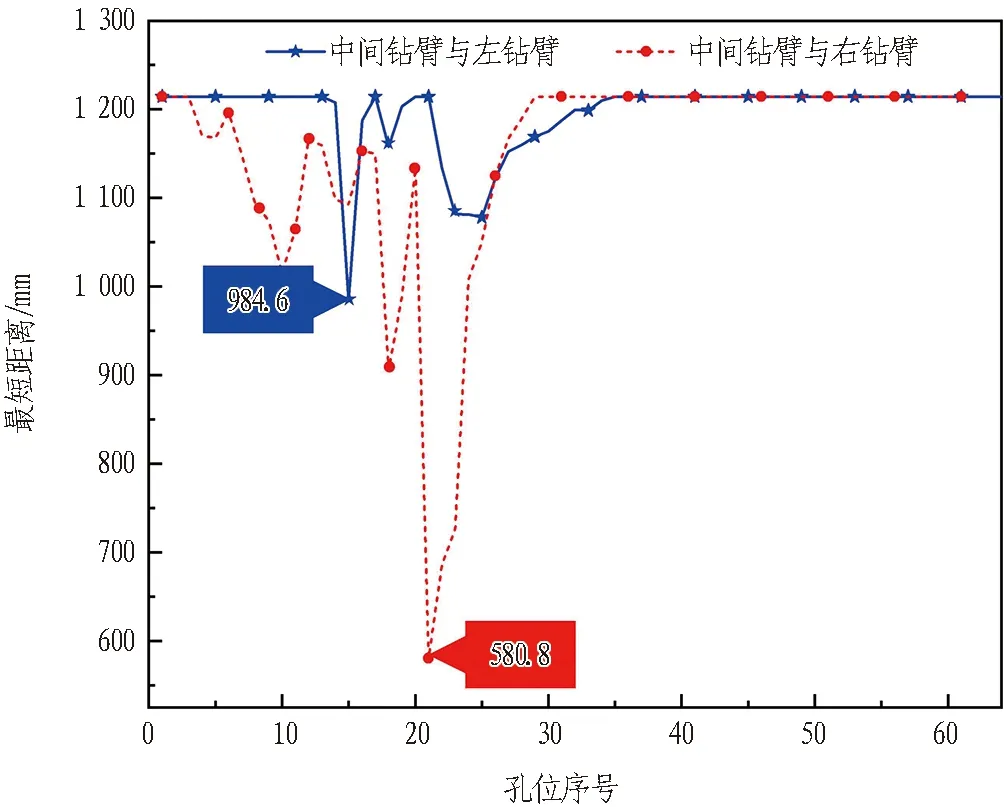
图9 基于距离最短钻孔顺序时钻臂之间最短距离

由图9可以看出,中间钻臂与左右钻臂之间的最短距离分别为984.6、580.8 mm,当中间钻臂与左右钻臂协同钻孔时均没有发生碰撞,由此可知所用改进人工势场法可以实现钻臂无碰撞钻孔作业,能够满足三臂凿岩台车钻臂协同钻孔作业要求。

3.2 基于关节变量最小钻孔顺序的路径规划化

3.2.1 实验仿真

依据图6(b)所示,各个钻臂起始点分别对中间钻臂与左钻臂、中间钻臂与右钻臂进行无碰撞路径规划仿真,结果如图10和图11所示。

图10(a)、11 (a)分别为中间钻臂与左右钻臂和开始钻孔任务时的初始状态,该姿态由三臂凿岩台车车体定位实现,在车体定位过程中,钻臂之间不会发生碰撞; 图10(b)、11(b)为中间钻臂完成工作区域内钻孔任务后2个钻臂之间状态,此时中间钻臂完成钻孔任务处于停止状态,左右钻臂继续钻孔作业; 图10(c)、11(c)为2个钻臂均完成钻孔任务后的工作状态。由图10和图11可知,2个钻臂在钻孔时完全按照所优化的钻孔顺序进行。

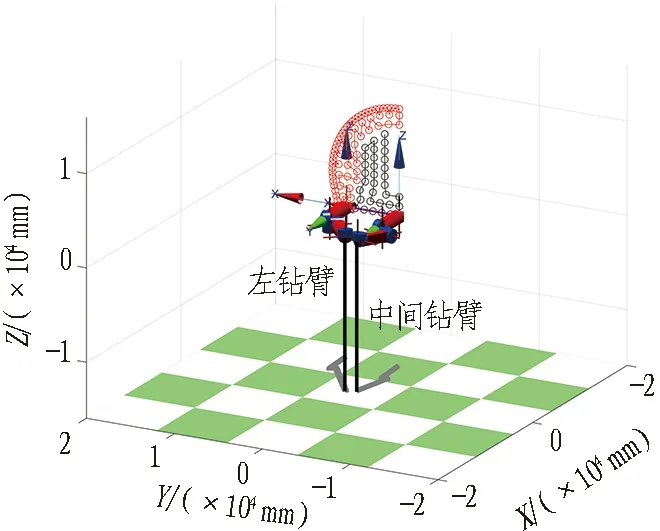
(a) 两钻臂初始工作姿态

(b) 中间钻臂完成钻孔任务

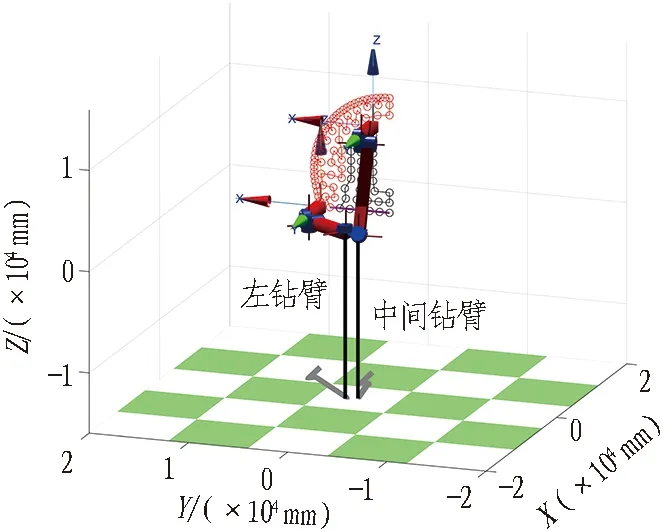
(c) 两钻臂完成钻孔任务

(a) 两钻臂初始工作姿态

(b) 中间钻臂完成钻孔任务

(c) 两钻臂完成钻孔任务

3.2.2 碰撞判定

进一步对钻臂简化后各包络盒之间的距离依据从大到小进行排序,并提取2个钻臂同时钻孔时各包络盒之间最短距离,以判断2个钻臂之间是否发生碰撞。钻臂之间最短距离如图12所示。可以看出,中间钻臂与左右钻臂之间的最短距离分别为193.5、580.8 mm。

综合考虑钻臂实际结构,如钻臂各关节外壳尺寸、钻孔施工安全等因素,中间钻臂与左钻臂之间存在碰撞的风险。

图12 基于关节变量最小钻孔顺序时钻臂之间最短距离

4 结论与讨论

1)基于改进的D-H法得到三臂凿岩台车运动学模型。为简化计算过程、提高运算效率,依据钻臂各关节结构特点,采用圆柱体+长方体的包络盒法对钻臂模型进行合理简化,基于包络体模型建立碰撞干涉检测数学模型。

2)对传统势场法中势场函数重建,将势能引入钻臂各关节,保证势场对钻臂位姿有约束作用,钻臂按照优化后钻孔顺序工作,基于改进人工势场法对钻臂进行位姿调整规划。仿真结果表明,基于距离最短钻孔顺序所得中间钻臂与左右钻臂之间的最短距离分别为984.6、580.8 mm,均未发生碰撞干涉; 基于关节变量最小钻孔顺序所得中间钻臂与左右钻臂之间的最短距离分别为193.5、580.8 mm。此时,综合考虑施工安全性及钻臂结构尺寸,存在碰撞风险,故在钻孔施工时,应选取钻臂末端移动距离作为优化目标时所得的钻孔顺序,此时可以实现三臂凿岩台车3个钻臂协同无碰撞钻孔施工。

考虑到现场作业中岩石硬度质地不同会导致凿岩车出现卡钻、断钎等问题,需要针对不同工况及时调整凿岩车的钻进参数,有必要结合自适应钻进开展进一步研究。