盾构掘进姿态自动控制技术研究与应用

简 鹏, 杨 晨, 游宇嵩, 荆留杰, 臧家琪, 徐受天

(中铁工程装备集团有限公司, 河南 郑州 450000)

0 引言

盾构法隧道施工过程中,对于盾构的姿态控制有极高的要求,然而由于地质条件复杂、测量环境恶劣等因素,使得盾构的掘进方向很难与隧道设计轴线保持一致,常常会出现水平或者垂直偏差过大,从而对项目的工期、成本和安全造成重大影响[1]。当前,盾构掘进过程中依然是依靠人工进行推进控制,由主司机根据导向测量系统的反馈值来调节油缸压力,这种依赖人工经验的操作方法具有较大的局限性,很难保证隧道的成型质量。

为保证盾构隧道成型质量及施工过程的安全性,提高盾构施工智能化水平[2],国内外众多学者对盾构姿态控制进行了深入研究。国外关于盾构姿态智能控制的研究主要分为2个阶段: 第1阶段以理论研究为主,代表学者有酒井邦登、桑原洋、仓冈豊、清水贺之、Grima等[3],分别采用卡尔曼滤波理论、模糊控制技术、神经网络等方法对盾构姿态控制进行了有意义的探索。第2阶段以生产应用为主,日本清水建设开发了智能盾构操作系统,通过人工智能算法建立了AI模型,可实现管片自动选型和盾构自主掘进[4];马来西亚MMC公司基于大量历史掘进数据进行学习建模,结合盾构经验控制方法及规则,开发了盾构自主掘进系统,该系统可实现盾构姿态和推进过程的自动控制,但是这种基于数据驱动的控制模型需要大量的训练样本,而且无法解决掘进姿态突发事故。

虽然国内开展盾构相关研究时间较晚,但是亦取得了丰硕的成果。刘成等[5]从水平和垂直2个方向考虑盾构的姿态控制问题,分析了最小纠偏半径、纠偏力矩的相应公式,建立了盾构水平方向的纠偏曲线模型,并对其进行了模拟。龚国芳等[6]基于模糊PID方法,提出一种盾构掘进姿态的控制策略,可实现盾构掘进轨迹、掘进速度的准确控制,并通过仿真和试验验证了其控制效果。张爱军[7]运用BP神经网络模型对掘进速度、刀盘转速、刀盘转矩、油缸压力差等参数对盾构隧道轴线偏移量的影响进行了深入研究,得到了盾构施工参数对姿态控制的影响及其规律。邵诚俊等[8]研究了盾构的多个子系统,得到了关于水平方向的姿态纠偏系统模型,并且分析设计了相应的控制器进行控制研究。李洋[9]以最短纠偏轨迹为目标,利用改进的人工蜂群算法优化盾构纠偏模型,开展了地铁隧道盾构姿态智能控制的研究,为盾构纠偏提供辅助决策。刘肖楠[10]提出一种基于粒子群算法优化的PID控制器参数的纠偏控制策略,设计了以液压推进系统的纠偏控制器,可以实现纠偏控制的快速响应。

虽然已有众多学者做了相关研究,但是目前国内对于盾构姿态自动控制方面的研究依然处于理论阶段,所提出的控制策略和方法基本没有在现场得到规模化应用。本文基于模糊控制及最佳纠偏曲线模型,研究盾构的姿态自动控制技术,并在现场进行测试应用,以期为姿态控制提供坚实的基础。

1 最佳纠偏曲线模型建立

盾构纠偏是通过调整分区液压油缸压力或其他手段控制盾构的掘进方向,使盾构的掘进轨迹逐渐靠近隧道设计轴线(designed tunnel axis, DTA),最终与设计轴线重合,同时确保纠偏后盾构切口方向与DTA重合。盾构纠偏轨迹如图1所示。

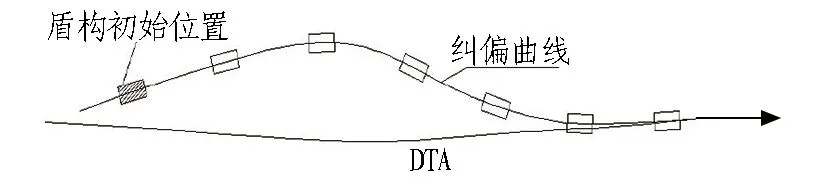
图1 盾构纠偏轨迹图

目前,盾构姿态纠偏曲线模型主要有3种: 1)以3次抛物线为基础的纠偏曲线模型; 2)以连续反向圆曲线为基础的纠偏曲线模型; 3)以对称螺旋曲线为基础的纠偏曲线模型[10]。纠偏曲线的本质是一种最优路径规划,设计一条满足各种约束条件的盾构始末状态相连的运动轨迹,需满足的约束条件实际上就是对最小纠偏半径的约束。本文采取连续反向曲线的纠偏模型,纠偏原理如图2所示。

图2 盾构纠偏原理图

1.1 最小纠偏半径确定

盾构掘进的姿态控制过程中,使纠偏轨迹最短所采用的纠偏半径称为最小纠偏半径,盾构在曲线纠偏时半径不能小于最小纠偏半径,否则易引起盾尾间隙减小,甚至造成管片破损。因此,为保证盾构正常掘进,需要保证纠偏时的曲线半径大于最小纠偏半径。最小纠偏半径由盾尾间隙、推进油缸行程差等因素共同决定,需要同时考虑多参数的影响。

1.1.1 盾尾间隙决定的纠偏半径R1

盾尾间隙是指盾尾与管片之间的距离,纠偏过程中若纠偏半径过小,超过盾尾间隙范围,会使管片与盾尾接触而产生干涉,严重时会引起盾尾挤压管片,甚至导致管片破损。对于盾尾间隙决定的纠偏半径计算,已有学者进行研究,参考其研究成果[11-12],得到纠偏半径

(1)

式中:R为管片半径,m;δ为靠近转弯中心一侧的盾尾间隙,m;l为管片宽度,m。

1.1.2 油缸行程差决定的纠偏半径R2

盾构转向时,曲线外侧油缸行程比内侧的大,使得推进油缸产生行程差。在实际盾构施工中,一般要求油缸行程差不超过50 mm,对应的最小纠偏半径

(2)

式中:RF为推进油缸半径,m;ls为盾构刀盘切口至盾尾的距离,m。

最小纠偏半径除受到上述因素的影响外,还受到盾构几何尺寸所允许的最小转弯半径R3、隧道设计转弯半径决定的最小转弯半径R4的限制,因此可得最小纠偏曲线半径

Rmin=max (R1,R2,R3,R4)。

(3)

1.2 纠偏曲线模型

由图2可知,线段OD是隧道设计轴线(DTA),直线AB是盾构当前位置,弧BCD是纠偏曲线,纠偏起点B所在的纠偏曲线方向和当前盾构前进方向相切,纠偏终点D所在的纠偏曲线切线方向和设计路线相切,弧BC和CD是半径相同的圆曲线。纠偏曲线模型的半径是上述所得最小纠偏半径Rmin,可保证盾构在最短路程内靠近隧道设计轴线。

假设此时盾构AB与设计路线OD的夹角为θ,切口水平偏差为h,即点B到直线OD的垂直距离为h,令第1段纠偏圆曲线l1的圆心角为α,第2段纠偏圆曲线l2的圆心角为β,纠偏曲线要使盾构在最短时间内安全地从当前位置向隧道设计轴线靠近,根据上述要求可得出盾构最佳纠偏曲线模型见式(4)。

(4)

式中:x、y为盾构纠偏路径各点相对于隧道设计轴线的坐标值;α、β为未知量,可由式(5)计算得到。

(5)

由式(4)—(5)可计算得出盾构最佳纠偏曲线相对于隧道设计轴线的水平偏差值ΔH、垂直偏差值ΔV及水平趋势值ΔT1、垂直趋势值ΔT2。

2 模糊控制器设计

2.1 模糊控制器的输入、输出变量

盾构掘进过程中,主司机根据盾构的位姿参数来确定各分区液压缸的设定压力和行程,一般将水平方向和竖直方向分开来进行考虑。基于此,本文将水平方向和竖直方向的切口偏差值和趋势值作为模糊控制器的输入变量,将分区油缸压力差(水平或竖直方向)作为输出变量。模糊控制器的输入、输出变量如图3所示。

H为切口水平偏差,mm; T1为水平趋势值,mm/m; ΔFh为左右分区油缸压力差,mm; V为切口垂直偏差,mm; T2为垂直趋势值,mm/m; ΔFv为上下分区油缸压力差,mm。

2.2 模糊控制规则

模糊规则是对人工操作经验和专家知识的总结,并根据现场地质条件和掘进数据对控制规则进行修正和完善。一般情况下,当盾构距离DTA偏差值较大且趋势值较大时,分区油缸压力差也应该增大;当偏差值较小时,应该防止超调,以保持稳定性为主。

盾构隧道设计轴线一般可分为直线段、缓和曲线段、曲线段3种类型,原则上每种曲线类型所对应的模糊规则不相同,因此水平、垂直方向需要各构建3个模糊控制器,用以应对不同掘进曲线状态。

本文采用具有2个输入参数的规则对姿态进行控制,输入变量为切口偏差和趋势值,以直线段水平方向姿态控制规则为例,如表1所示。

表1 直线段水平模糊控制规则

2.3 模糊推理及去模糊化

模糊推理输出的结果是一个模糊集合,但是盾构的姿态只能以精确量控制执行机构动作,因此必须从模糊集合中判决出一个精确量。本文采用加权平均法法进行模糊判决,可以充分利用输出模糊集合所包含的所有信息。

反模糊解可通过Matlab编程快速实现,得到输入与输出变量之间的关系表,即模糊控制表。盾构姿态模糊控制流程如图4所示。

图4 盾构姿态模糊控制流程图

3 盾构姿态自动控制系统设计

盾构施工时,可通过改变推进油缸或铰接油缸压力进行姿态的控制。但是实际掘进过程中,操作人员为了保证铰接油缸状态的稳定,往往会保持铰接油缸压力、位移不变。因此,该系统考虑采用调节推进油缸压力来实现姿态的自动控制。

3.1 数据采集

该系统可直接从PLC读取盾构姿态参数、分组油缸压力等数据,具体涉及的参数如表2所示。

表2 数据采集表

3.2 数据分析

3.2.1 输入参数分析

对盾构姿态参数进行分析,当偏差值和趋势值在允许范围(一般规定偏差允许值为±50 mm,趋势值为±10 mm/m)时,输入参数为姿态偏差值H、V和趋势值T1、T2;当盾构偏差值和趋势值超出允许范围时,构建最佳纠偏曲线,获取盾构最佳纠偏曲线相对于隧道设计轴线的水平偏差值ΔH、垂直偏差值ΔV及水平趋势值ΔT1、垂直趋势值ΔT2,最终输入参数为盾构位姿相对于最佳纠偏曲线的相对偏差值H′、V′和相对趋势值T1′、T2′,相对偏差值和相对趋势值由式(6)计算所得。

(6)

3.2.2 输出参数分析

模糊控制器输出参数为分组油缸压力差,需要对该压力差进行分配以实现姿态控制。为保证总推力不变或者变化极小,从而减小对推进速度、土舱压力的影响,油缸压力差的改变按照A/C、B/D 2组油缸一增一减的方式调整,若当前的油缸压力差值与输出值一样,则保持当前参数掘进;若不一样,则按式(7)进行分配。

(7)

式中: ΔFA、ΔFB、ΔFC、ΔFD分别为A、B、C、D 4组油缸压力调整值;ΔFh为模糊控制器输出水平方向油缸压力差;ΔFh′为当前水平方向油缸压力差;ΔFv为模糊控制器输出垂直方向油缸压力差;ΔFv′为当前垂直方向油缸压力差。

3.3 控制流程

盾构掘进过程中,导向系统根据测量结果显示盾构当前位姿与隧道设计轴线之间的偏差,当偏差量较小时,一般通过调节油缸压力差进行姿态控制,此种情况下可根据模糊控制器输出的压力差值进行油缸压力调整;当偏差较大超出允许范围时,为了使盾构掘进快速、安全地恢复到正常姿态,则需要根据纠偏曲线进行姿态控制,模糊控制器的输入参数为盾构位姿相对于纠偏曲线的偏差值、趋势值。

将上述所述盾构偏差值及趋势值输入盾构姿态模糊控制器,并得到相应的水平、垂直油缸压力差,若当前的油缸压力差值与输出值一样,则保持当前参数掘进;若不一样,则重新进行压力分配,并将最终油缸压力值下发至PLC,由PLC执行姿态控制动作。盾构姿态自动控制流程如图5所示。

图5 盾构姿态自动控制流程

4 现场测试

该盾构姿态自动控制系统在成都地铁10号线某区间进行测试,测试期间隧道埋深约7.5 m,测试环号为501—533环,其中514—525环由自动控制系统掘进,剩余由人工掘进。盾构穿越地层为上部松散砂卵石土、下部稍密砂卵石土,地下水较丰富。

设备直径为6.41 m,推进油缸共20根,分为A、B、C、D 4组,由于测试期间盾构处于右转弯区间段且位于复合地层,根据项目要求需要保证切口水平偏差在(5 mm,10 mm)区间,水平趋势值大于0 mm/m,切口垂直偏差在(-10 mm,-5 mm)区间,垂直趋势值大于7 mm/m,对比人工掘进与自动掘进,姿态控制结果如图6所示。

(b) 垂直方向掘进姿态偏差值

由图6可以看出,在514—525环自动掘进段内,盾构姿态控制效果较好,盾构姿态偏差值都控制在允许的范围内,当姿态偏差值接近允许值时,基于模糊理论的控制系统迅速做出反应并调整分组油缸压力差,使得掘进姿态恢复至合理值。同时,相比于手动掘进,自动掘进时盾构姿态偏差的波动更小,这是因为自动掘进时对于掘进参数的调整频率比手动掘进时高,且手动掘进时主司机自主性比较大,只需保证偏差值在合理范围即可。总体来讲,该系统基本可以满足盾构姿态自动控制的需求。

由于在现场测试过程中,并没有出现姿态偏差超出允许范围的情况,故没有对纠偏曲线模型的合理性及准确性进行验证,因此下一步需要进行多工况下的系统可靠性测试。

5 结论与建议

盾构姿态的自动控制是实现盾构智能化的必由之路,也是整个盾构行业的未来发展趋势。本文结合实际工程项目,开发以模糊理论和纠偏曲线为核心的姿态控制系统,实现了盾构掘进的自动控制目标。

1)设计了盾构最佳纠偏曲线模型,该模型可以在盾构姿态偏差过大时进行纠偏,实现盾构掘进轨迹快速、安全地靠近DTA附近。

2)利用模糊控制理论,设计了姿态模糊控制规则,构建了盾构掘进姿态模糊控制器。

3)设计了盾构姿态自动控制系统,并对该系统进行了现场应用测试,结果表明该系统具有较高的可靠性和实用性。

盾构掘进工况复杂多变,本文仅验证了右转弯时的控制准确性,但对于姿态偏差过大时的情况未进行测试,后续需要在多种工况下对该系统进行测试并完善。