端部锚固锚杆预应力场分布特征研究

訾 信, 汪 波, 喻 炜, 钟官峰

(西南交通大学 交通隧道工程教育部重点实验室, 四川 成都 610031)

0 引言

近年来,随着预应力锚杆(索)系统在木寨岭公路隧道等软岩大变形地下工程中的成功应用[1-4],预应力主动支护技术为软岩隧道大变形控制开辟了新的途径。与隧道常用全长黏结式锚杆不同,树脂端锚+后注浆型预应力锚固系统在满足耐久性需求的基础上具有使围岩中形成更大预应力扩散范围的能力[5-7],这也是主动支护得以调动和发挥较深部围岩自承能力的基础[8]。

对预应力锚杆支护机制的探究离不开对其在围岩中产生的应力场的研究。现有研究中,对锚杆所形成的围岩预应力场的分布规律研究主要为不同锚固系统参数对围岩预应力场分布规律的影响。例如: 顾金才等[9-10]通过室内试验和数值模拟,研究了均质岩体中单根预应力锚杆的加固范围,并分析了锚杆长度和预应力值对锚固范围的影响;康红普等[11-12]通过数值模拟和室内试验研究了不同预应力下锚杆、锚索产生的应力场分布特征,以及钢带对锚杆预应力扩散的作用;张镇等[13]采用数值模拟,研究了锚杆(索)施加不同组合预紧力时围岩产生的应力场分布特征与规律;王文才等[14]采用数值模拟研究了锚杆长度和预紧力对围岩中产生的附加应力场的影响;林健等[15]通过室内试验研究了预应力端部锚固锚杆预应力场在围岩体中的分布特征;王晓卿等[16]通过数值模拟研究了原岩应力条件下不同黏结刚度预应力锚杆对层状顶板的支护作用;李建忠等[17]通过数值模拟研究了原岩应力场作用中不同预紧力及不同支护密度下锚杆支护的应力场;刘林胜等[18]通过数值模拟研究了锚杆在不同预应力下的支护效果差异。

既有研究中,试验数据采集多采用单点式测量元件,未能实现测线全长范围内的数据采集;且对不同锚杆参数下围岩应力场分布的研究多集中于矩形断面巷道中,而在马蹄形断面交通隧道中还少有研究。故本文将采用分布式光纤进行单根预应力锚杆应力场测试,并在马蹄形断面围岩中研究不同锚杆参数下预应力场分布规律,以期为预应力锚固系统作用机制研究提供一种思路。

1 单根锚杆室内试验

1.1 试验材料及传感器布置

为研究单根锚杆预应力扩散效应,开展室内锚杆拉拔试验。以混凝土试块模拟围岩[19],所浇筑的C35混凝土试块尺寸为0.5 m×0.5 m×1 m,配合比为水泥∶砂∶石=400∶980∶1 160,外加剂质量比为0.3,中心留直径0.04 m、长0.8 m的孔。混凝土弹性模量可取31.5 GPa,泊松比取0.2[20]。Q345锚杆内直径为0.015 m,外直径为0.025 m,长1.3 m。混凝土预留孔底部0.3 m范围内用树脂进行锚固。由于工程中预应力主动支护锚固系统在预应力锁定后才进行后注浆[1,8],故该试验未考虑后注浆。锚杆抗拉强度不低于470 MPa,断后伸长率不低于20%[21]。

采用微机电子万能试验机通过单轴压缩试验测得所用树脂材料(见图1)弹性模量为13.2 GPa,泊松比为0.17。

图1 树脂试件

为测得锚杆预应力在试块中所产生的沿锚杆轴向的应力场分布,在浇筑混凝土时预埋2片布设应变测量传感器的钢筋网,钢筋直径为0.006 m,其中一片布有30个应变片,另一个则布有分布式光纤,传感器布置方案见图2。考虑到试验加载条件下,除加载端面外混凝土内响应应变较小,可认为浇筑于其中的钢筋网与混凝土协同变形,故可近似将光纤所测得的钢筋应变视为混凝土应变。

(a) 实物图

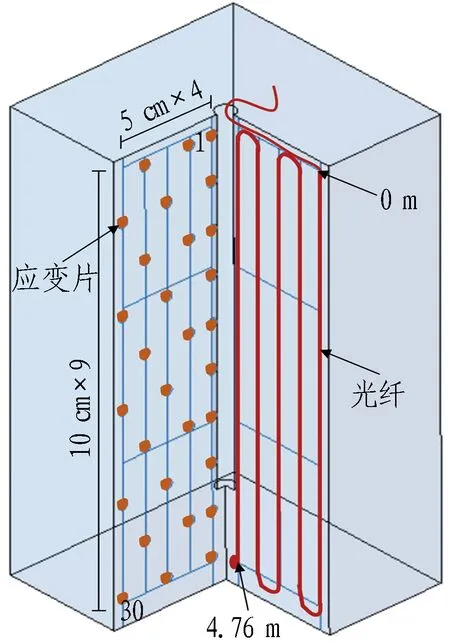
(b) 示意图

分布式光纤数据和应变片数据分别由OBR4600光背向反射仪和TST3826F静态应变测试分析系统处理得到,主要试验仪器见图3。通过锚杆拉拔仪进行预应力的施加,由带数显的手动泵按5 kN左右1级,逐级施加预应力至60 kN左右停止。

图3 主要试验仪器

1.2 结果分析

不同预应力量值下,分布式光纤测得的应变沿长度变化规律如图4(a)所示。有效光纤长度为4.76 m,定义内端为起始点0,外端为终点4.76 m处(见图2(b)),各区段0～0.95 m,0.95～1.91 m,1.91～2.86 m,2.86～3.81 m与3.81～4.76 m分别对应距锚孔0.21、0.16、0.11、0.06、0.01 m(最靠近锚孔处)的测线数据。可以看出,距锚孔不同距离处,应变沿深度的分布均由大范围的压应变区和小范围的拉应变区组成。由图4(b)可知,压应变在垫板端面最大,随远离垫板端先快速减小而后又增大到第2个压应变极值,随后减小到转变为拉应变;2个压应变极值和1个拉应变极值分别出现在距垫板端面约0.02 m、0.52 m和0.69 m处。

由图4(a)可以看出,应变量值随施加预应力的增大而明显增大。在距锚孔0.01 m(最靠近锚孔)处,施加60.09 kN预应力时,2个压应变极值分别为-106 με和-37.9 με,拉应变极值则为18.5 με。在施加50.19 kN、40.25 kN和30.31 kN预应力时,最大压应变极值分别为-64.4 με、-54.7 με和-38.8 με。同时,应变量值随靠近锚孔而明显增大。施加60.09 kN预应力时,在距锚孔0.06 m处,2个压应变极值分别为-55.1 με和-16.5 με,拉应变极值则为4.2 με。在距锚孔0.06 m、0.11 m和0.16 m处,最大压应变极值分别为-55.1 με、-16.6 με和-12.5 με。可以看出,预应力诱发应变量值减小速度随远离锚孔逐渐减小。

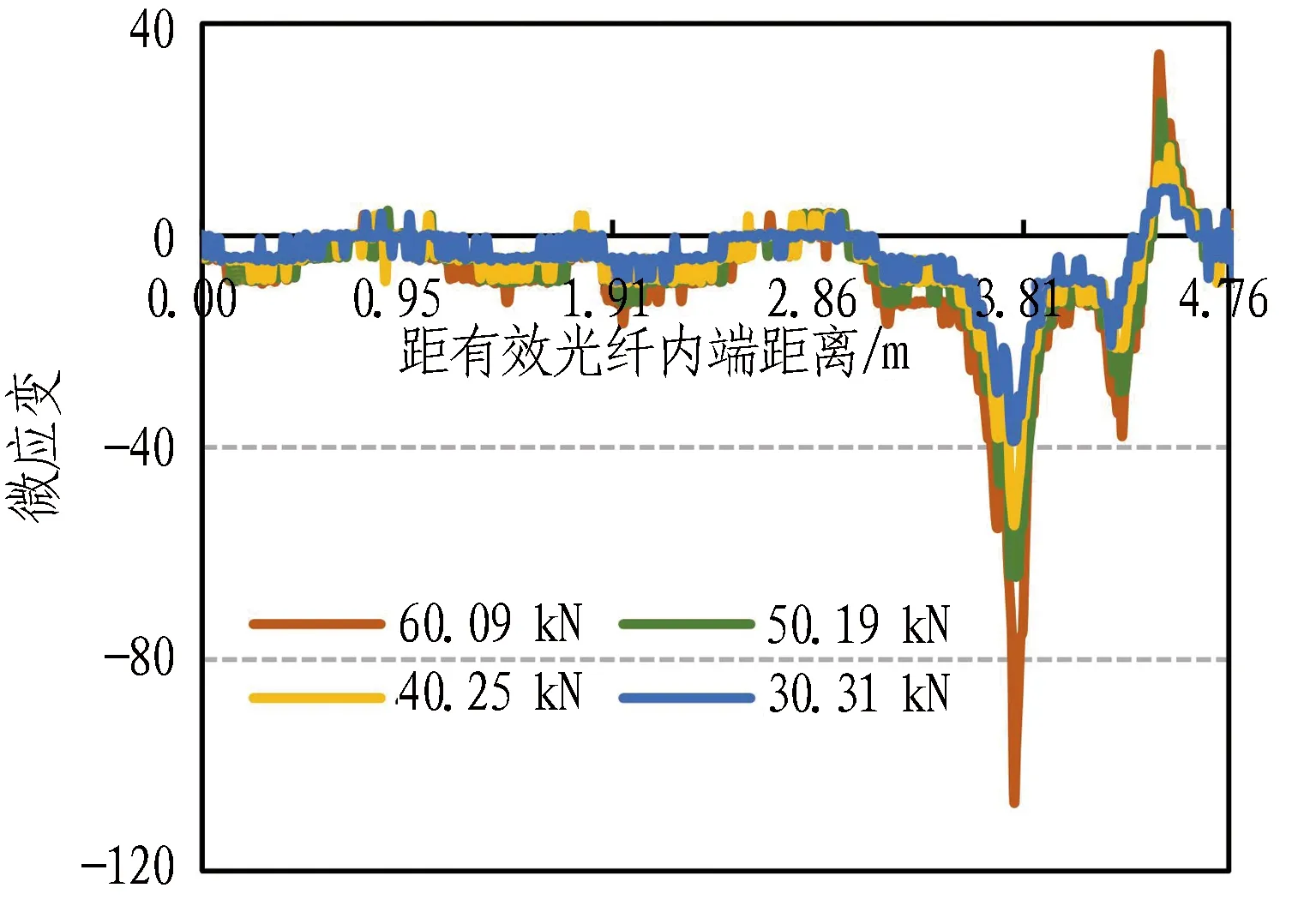
(a) 沿分布式光纤长度方向的应变分布规律

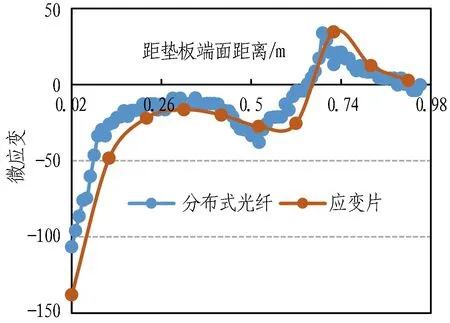
(b) 分布式光纤/应变片应变数据对比

提取施加预应力60 kN左右时,最靠近锚孔处(距锚孔0.01 m)测线上分布式光纤与应变片测得的应变数据作图,如图4(b)所示。可以看出,2种方式所测得的应变量值和分布规律均较为一致。

对上述端部锚固锚杆作用现象的微观机制作进一步定性分析[22],锚杆支护下杆体结构受力状态如图5所示。在自由段内不存在围岩-锚杆摩擦接触,因此该区段内轴力大小等于杆体所承受的拉拔力;在锚固段内,锚固剂与围岩存在黏结作用,在施加预紧力后锚固段范围内围岩受到沿钻孔壁分布的黏锚力作用,因此杆体轴力逐渐减小为0。

图5 锚杆支护下杆体结构受力状态

结合自由段-锚固段交界面和“两压一拉”的空间位置关系,可将其进一步分为3个区域(见图5)。区域Ⅰ为垫板作用下的压应力集中区,该区域由于垫板作用锚杆对围岩反向挤压,在混凝土表面附近形成了较大的压应力集中区。可以预见,该区域压应力最大值位于垫板作用位置,且随着远离垫板位置,压应力区域逐渐扩展贯通并与区域Ⅱ相连接。区域Ⅱ为黏锚作用下的压应力集中区,由锚杆支护围岩受力状态可知,该应力峰值在自由段和锚固段接触面附近(见图5)。该峰值产生的原因在于在锚固段内,锚杆通过锚固剂与围岩黏接在一起,在预应力作用时,钻孔内壁受到锚杆剪力即黏锚力作用,使锚固段围岩整体对下方围岩产生压力,从而形成了黏锚作用下的压应力集中区。区域Ⅲ为内锚段拉应力集中区,锚固段内围岩受力表现为在锚孔内壁沿锚杆轴线方向向下的非均匀黏结力,黏锚力由自由段向锚固段呈先增大再减小的规律。在此非均匀黏锚力作用下,内锚固段围岩产生拉力作用,从而使得锚杆锚固段的部分范围产生了明显的拉应力集中区。

2 单根锚杆预应力场分布规律

2.1 模型建立

为与前述试验保持一致,ABAQUS中模型总体尺寸设置为0.5 m×0.5 m×1 m(见图6(a)),中心留直径0.04 m、长0.8 m的孔,孔内布设预应力锚杆系统,模型底面6个自由度全部约束。预应力锚杆系统由0.15 m×0.15 m×0.01 m的垫板,内直径0.025 m、外直径0.038 m、厚0.024 m的螺母,内直径0.025 m、外直径0.040 m、长0.3 m的树脂锚固体以及内直径0.015 m、外直径0.025 m、长1.3 m的锚杆体组成(见图6(b)),其中锚杆体置于围岩内0.8 m。锚杆体、螺母、垫板及树脂锚固体采用弹性本构,试块采用Mohr-Coulomb理想弹塑性本构[23],材料物理力学参数如表1所示。围岩-垫板、围岩-锚固体、锚固体-锚杆、垫板-螺母及螺母-锚杆间均采用tie接触。此外,锚杆以实体单元建立,采用bolt load荷载施加预应力,预应力量值为60 kN,且不考虑材料自重。

(a) 整体模型

(b) 锚杆系统

Fig. 6 Model establishment

表1 材料物理力学参数

2.2 结果分析

预应力在试块中形成沿锚杆轴向方向应力S33,分布如图7所示。由图可知,锚杆垫板端锚孔附近围岩存在明显压应力集中,而在锚杆未锚固段和锚固段分界处围岩中出现了另一压应力集中区域,2处压应力集中区域压应力量值均在锚孔壁处最大,随远离锚孔壁而减小。锚杆尾端锚固段附近围岩中出现拉应力集中区域如图7(b)所示。由图可知,拉应力最大值同样出现在锚孔壁处,而随远离锚孔壁逐渐减小。

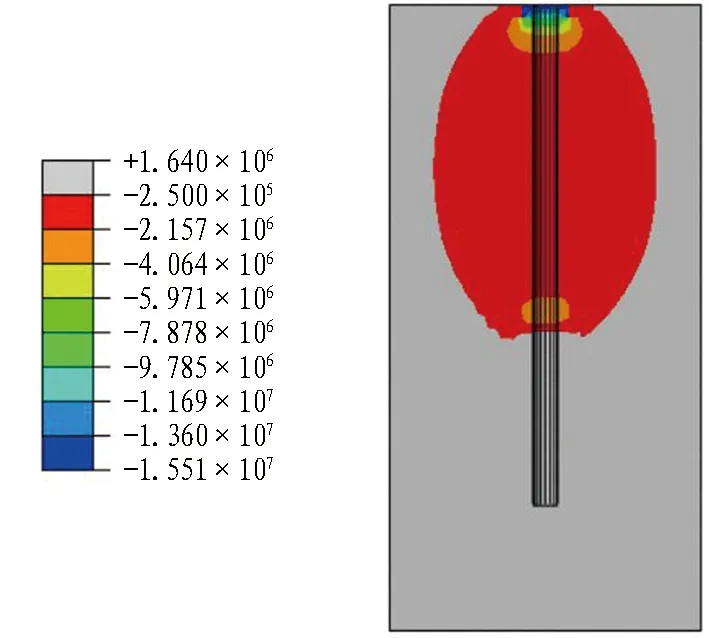
(a) 压应力区

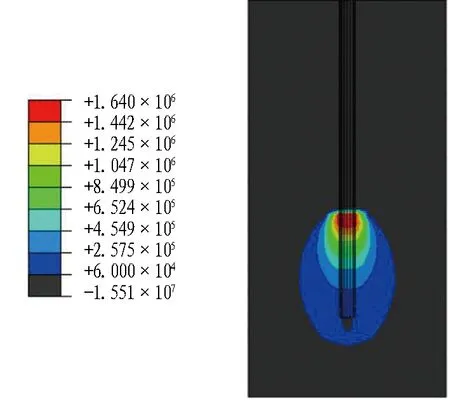
(b) 拉应力区

建立如图6(a)所示坐标系,坐标原点位于垫板端围岩表面锚孔中心处,提取不同锚间距x(某一研究面离参考锚杆锚孔中心的距离)及不同深度z处试块沿锚杆轴向应力S33作图,如图8所示。

(a) 不同锚间位置x处

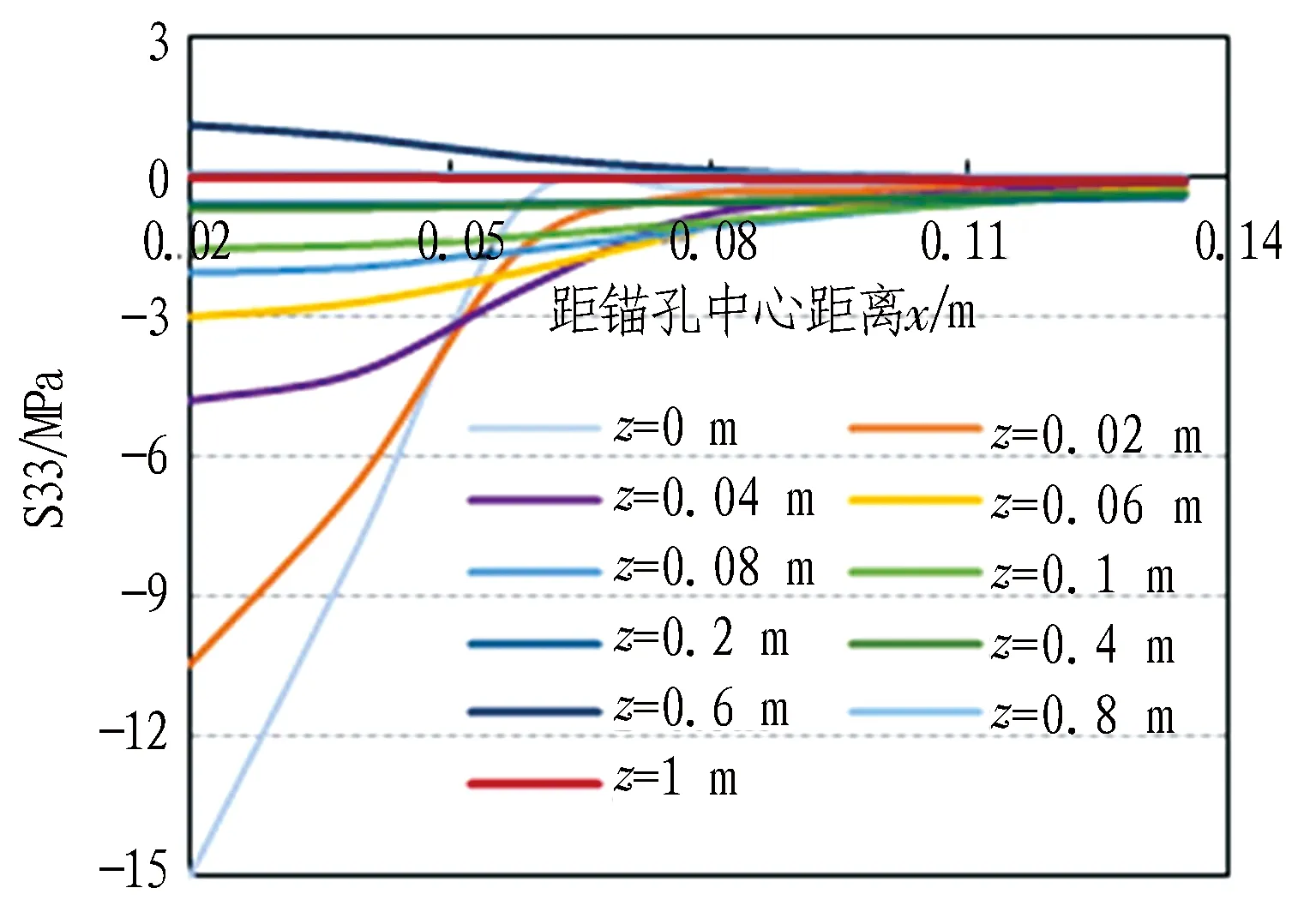
(b) 不同深度z处

由图8(a)可以看出,不同锚间距位置处围岩S33沿深度分布均存在2个压应力极值和1个拉应力极值,且第2大压应力和最大拉应力都分别出现在未锚固段靠近锚固段一侧和锚固段靠近未锚固段一侧,但最大压应力出现位置有所不同。较靠近锚杆处(x≤0.019 m)时,S33在垫板端面最大且随竖向深度z增大而减小;而在远离锚杆处(x>0.019 m)时,S33在垫板端面最小且随z先增大到最大值而后减小; 竖向应力最大值同样随x减小(靠近锚杆)而增大。锚孔壁(x=0.02 m位置)处S33分布规律与1.2节试验所测得的沿锚杆轴向试块应变分布规律较为一致,但拉应力峰值出现的位置略有不同。数值模拟结果中出现在z=0.56 m处(见图8(a)),而试验结果中出现在距垫板端面0.69 m处(见图4(b)),这可能是由于试验内锚段树脂不均匀或数值模拟未能较好考虑内锚段介质间接触所致。

不同关键深度z处S33分布如图8(b)所示。由图8(b)可知,越靠近垫板端(z较小),靠近锚杆处应力集中越明显,S33在x=0 m处最大且随x增大而减小,其衰减速度随z减小明显加快。而当z达到0.4 m后,S33沿锚间分布较为均匀。随着z增大到0.6 m后,靠近锚杆处再次出现应力集中,z继续增大后又趋于均匀。

为进一步研究不同锚固长度下锚杆预应力在试块中形成的竖向应力场分布规律,分别建立锚固长度为0.3、0.4、0.5、0.6、0.7、0.8 m的模型,其余参数与2.1节模型相同。锚杆预应力在围岩中形成的压应力扩散区对发挥锚杆挤压围岩效应至关重要,同时应结合围岩物理力学性状要求压应力达到一定量值。此处仅以0.25 MPa为例分析锚固长度对围岩压应力区分布的影响,如图9所示。由图可知,随锚固段长度的增加,S33>0.25 MPa的范围快速减小,这说明内锚段过长不利于压应力的扩散,故在满足锚固力要求的前提下,内锚段长度不宜选择过大[24-25]。

(a) 0.3 m (b) 0.4 m (c) 0.5 m

(d) 0.6 m (e) 0.7 m (f) 0.8 m

提取锚孔壁处S33进行分析,如图10所示。可以看出,当锚固长度为0.3～0.6 m时,S33在不同深度的极值大小一致,仅第2压应力峰值和拉应力峰值出现位置随锚固长度的变化发生偏移。具体来说,第2压应力峰值始终出现在对应未锚固段与锚固段分界面处,而拉应力峰值则出现在锚固段靠近未锚固段一侧。而当锚固长度达到0.8 m(全长锚固)时,锚杆预应力仅在垫板端附近0.05 m范围内形成压应力区,最大压应力出现在垫板端面,而后随z增大快速衰减,z>0.05 m范围为拉应力区,但拉应力量值较其他工况明显减小。综合上述结果,锚杆预应力所形成压缩带主要集中在未锚固段范围围岩中,而锚固段范围围岩中会形成不利的拉应力区。

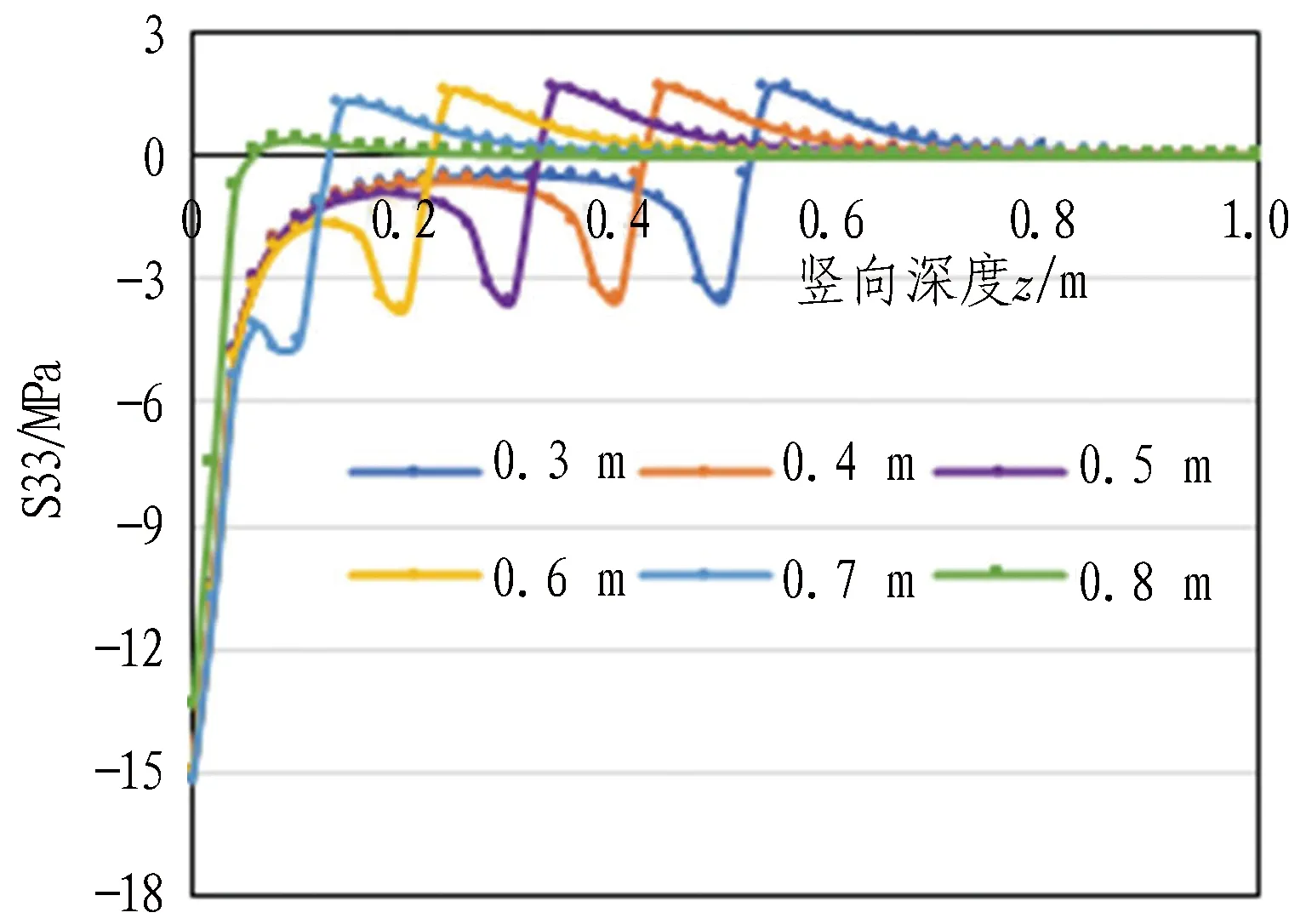
图10 不同锚固长度下孔壁竖向应力分布

3 隧道中群锚压缩带应力分布规律

3.1 模型建立

为进一步探究公路隧道中预应力群锚所形成的围岩压缩带中径向应力分布规律,在ABAQUS中建立模型,如图11所示。模型上、下与左侧边界约束法向位移,右侧边界则采用轴对称边界。考虑对称性,建立半边平面应变模型,尺寸为100 m×200 m,见图11(a);隧道断面见11(b)。围岩采用Ⅳ级围岩参数,如表2所示。所模拟的锚杆系统由杆体和垫板组成(见图11(c)),均采用梁单元模拟,材料为钢材(参数见表2)。杆体截面为外径0.025 m、壁厚0.005 m的中空锚杆,垫板尺寸为0.15 m×0.15 m×0.01 m。考虑到压缩带产生于锚杆压应力的扩散叠加[22],而前述分析证明压应力主要集中于锚杆自由段,因此以下模拟中未建立内锚固段,以着重探究杆体作用于围岩的挤压效果。围岩-垫板、围岩-锚杆内端及垫板-锚杆外端间均采用tie接触。此外,为重点研究锚杆预应力在围岩中形成的径向应力场分布,模型在既有开挖隧道基础上进行锚杆预应力的施加,采用降温法进行模拟。

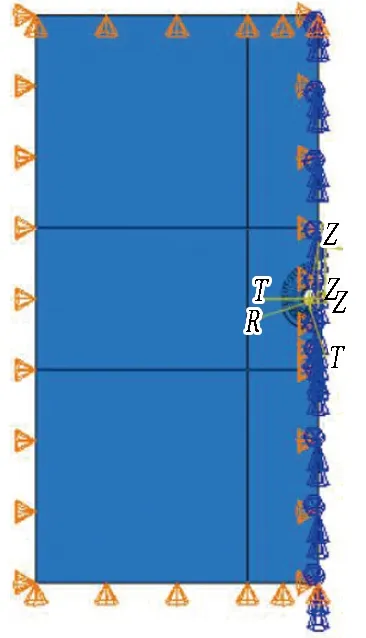
(a) 整体模型

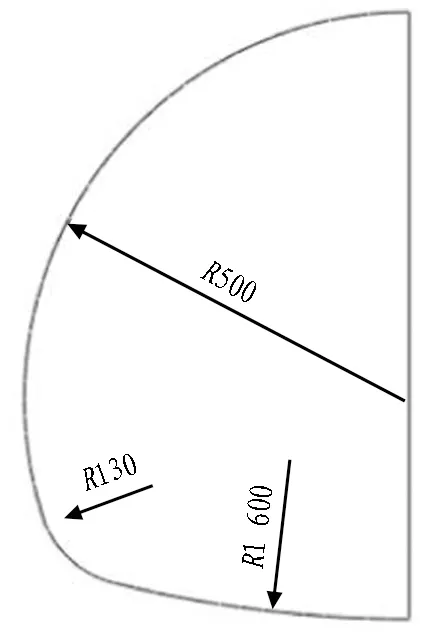
(b) 隧道断面(单位: cm)

(c) 锚杆系统(长5 m,间距0.8 m)

3.2 结果分析

采用间距0.8 m、杆长5 m的锚杆群,其在100 kN预应力作用下的围岩径向应力S11云图如图12(a)所示。由图可知,洞壁出现压应力集中,最大达0.874 MPa;内锚端则出现拉应力集中,最大达0.212 MPa;中部则出现压缩带,量值在0.06～0.15 MPa。考虑边界效应影响,以下选取拱腰处相邻2根锚杆进行分析。为进一步定量分析径向应力分布规律,提取不同锚间位置x及不同径向深度r处围岩径向应力σ3并做归一化处理后作图,如图12(b)和图12(c)所示,以研究预应力作用下杆体支护力的扩散程度和效率。图中,Fp为预应力量值;a和b分别为锚杆间距和排距。

由图12(b)可知,当r=(0.15～0.8)l(l为杆体长度)时,不同锚间位置处围岩σ3分布规律及量值较为一致,均从r=0.15l处的0.86Fp/(a·b)左右随r增大减小到r=0.8l处的0.58Fp/(a·b)左右。而当r超过0.8l后,σ3随r增大而先增大后减小,极大值随x减小(靠近锚杆)而增大。当r小于0.15l,较靠近锚杆处(x≤0.05 m)时,σ3在洞壁处最大且随r增大而减小;而在远离锚杆处(x>0.05 m)时,σ3在洞壁处最小且随r增大先增大到最大值而后减小,其最大值同样随x减小(靠近锚杆)而增大。

不同径向深度r处围岩径向应力σ3如图12(c)所示。由图可知,越靠近洞壁处(r较小),靠近锚杆处应力集中越明显,σ3在x/a=0处最大且随x/a增大而减小,其衰减速度随r减小明显加快,当r达到0.5 m后,σ3沿径向分布较为均匀。但随着r增大到4.8 m后,靠近锚杆处再次出现较明显应力集中,而后又趋于均匀,该规律与云图中两锚端出现尖角一致。

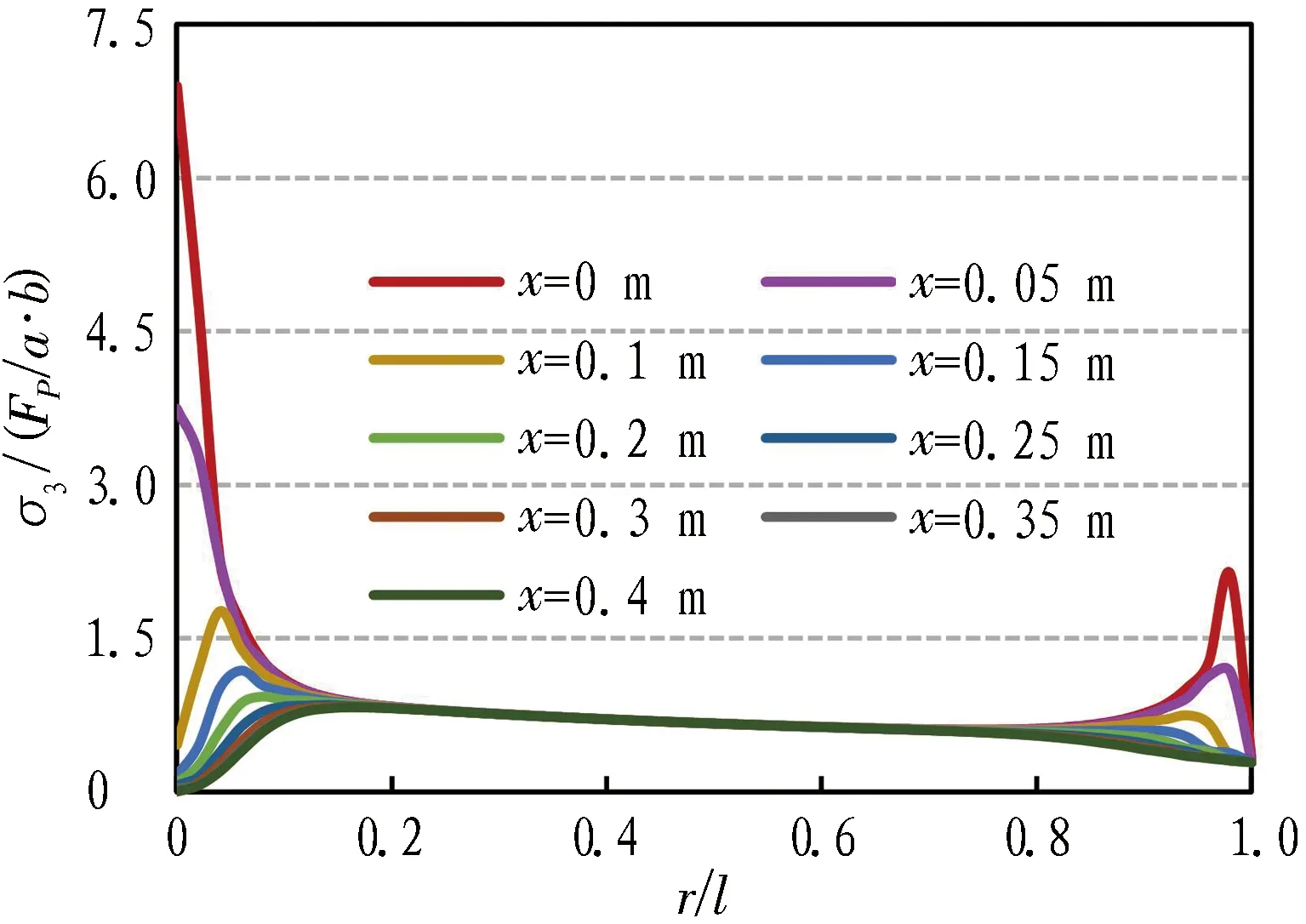
(b) 不同锚间位置x下

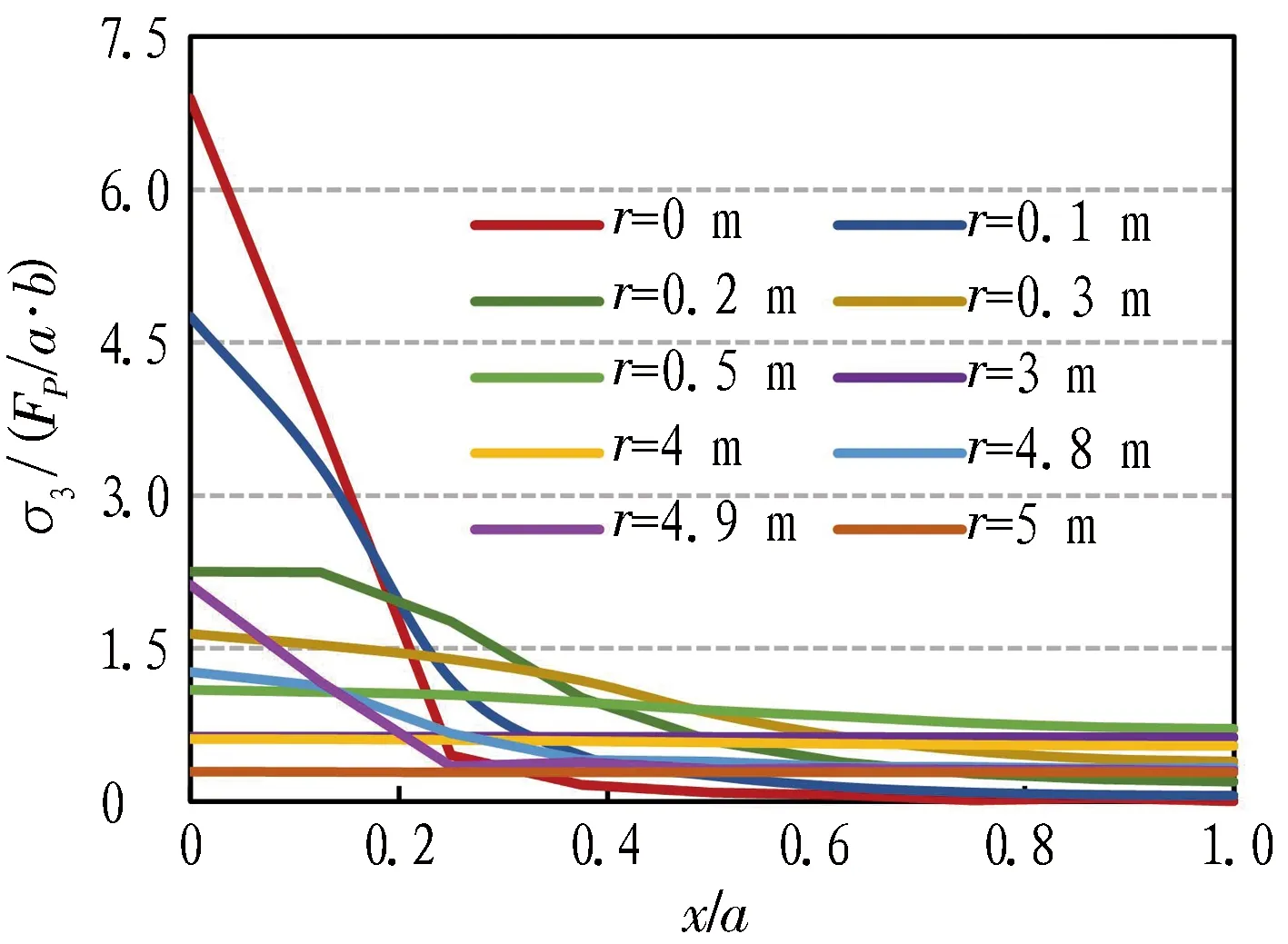
(c) 不同径向深度r下

3.2.1 不同预应力

为研究不同预应力时群锚在围岩中形成的径向应力场分布规律,分别施加60 kN、80 kN和100 kN预应力,并对预应力所形成围岩压缩应力的最低效用进行考虑。分析仅提取锚间x/a=1处σ3进行分析,如图13所示。由图可知,不同预应力作用下锚间x/a=1处σ3分布规律具有高度一致性,均随r/l先增大(r/l≤0.16)后减小,r/l达0.8后快速减小,而量值随预应力量值增大而呈线性增加。

图13 不同预应力量值下锚间围岩径向应力分布(x=0.4 m)

3.2.2 不同锚杆间距

为进一步研究不同锚杆间距下群锚预应力在围岩中形成的径向应力场分布规律,分别建立间距为0.6 m、0.8 m和1.0 m的群锚模型,杆体长度为5 m,施加预应力100 kN,其余参数与3.1节模型相同。基于对所施加预应力利用率的考虑,可将p′×(Fp/(a·b))作为判定压缩带范围的阈值,p′值为研究者所定容许预应力扩散效率。本文以p′=0.6为例进行分析,即认为径向应力超过0.6Fp/(a·b)范围为预应力有效压应力区。不同锚杆间距下围岩径向应力σ3超过0.6Fp/(a·b)范围如图14所示。由图可知,随间距减小(锚杆加密),连续压缩带厚度有所增大,且洞壁处未挤压区σ3<0.6Fp/(a·b))范围减小,不同间距下应力扩散角均约为30°。

(a) 0.6 m (b) 0.8 m (c) 1.0 m

提取锚间(x/a=1)处σ3进行分析,见图15。由图可知,不同间距下锚间σ3分布规律较为一致,最大值及压缩带范围均随间距减小而有增大,说明加密锚杆有利于增大压缩带范围。具体来说,σ3/(Fp/(a·b))最大值分别为0.865(间距0.6 m),0.826(间距0.8 m)和0.791(间距1 m),σ3≥0.6Fp/(a·b)范围分别为0.654l、0.618l和0.571l。

图15 不同间距下锚间围岩径向应力分布(x=0.4 m)

3.2.3 不同锚杆长度

为进一步研究不同杆体长度下群锚预应力在围岩中形成的径向应力场分布规律,分别建立杆长为3 m、4 m、5 m和6 m的群锚模型,杆体间距为0.8 m,施加预应力100 kN,其余参数与3.1节中模型相同。不同锚杆长度下围岩径向应力σ3超过0.6FP/(a·b)的范围如图16所示。由图可知,随杆长增大,连续压缩带厚度差异不大,且当杆长l>5 m时两锚端间无法形成连续压缩带,说明长锚杆应力扩散效果有限,无法在整个杆长范围围岩内形成压缩带。

(a) 3 m (b) 4 m

(c) 5 m (d) 6 m

提取锚间(x/a=1)处σ3进行分析(见图17),可以看出,不同杆长下锚间σ3分布规律较为一致,最大值基本相同,均为0.83FP/(a·b)左右,但其出现位置随杆长增大而越靠近洞壁,压缩带整体靠近洞壁转移。σ3>0.6FP/(a·b)范围差异不大,随杆长减小有所增大,说明短锚杆更易在杆长范围围岩内形成连续压缩带。

图17 不同杆长下锚间围岩径向应力分布(x=0.4 m)

3.3 压缩带应力分布规律

基于对所施加预应力扩散效率的考虑,本文将0.6Fp/(a·b)作为判定压缩带范围的阈值,即认为径向应力超过0.6Fp/(a·b)范围为预应力有效压应力区。保守考虑群锚预应力效应,可认为不同锚间位置处围岩径向应力分布规律与两锚杆中间处相同。基于上述假定,为进一步拟合压缩带内应力分布规律,可对前述数值模拟结果加以总结:

(1)

式中:m为两函数曲线相交时r/l的取值;常数项A—E与锚杆长度l和间距a有关。

以间距0.8 m工况为例,将拟合函数曲线与数值模拟结果对比,如图18所示。可以看出,拟合函数能较好地反映径向应力分布整体趋势。

图18 函数拟合和数值模拟下锚间围岩径向应力分布对比(x=0.4 m)

上述直观、简洁的函数拟合公式,可以较好反映不同的锚杆间距、预应力和长度下压缩带内应力分布规律,从而可对任意锚杆参数工况下预应力导致的围岩次生应力场进行先期预测。

4 结论与讨论

本文通过室内试验和数值模拟,先研究了不同锚固长度下单根预应力锚杆所形成应力的分布规律,并基于此进一步探讨了马蹄形隧道中预应力量值、锚杆间距与长度对隧道围岩预应力场分布规律的影响,得到主要结论如下:

1)端锚型锚杆预应力可在围岩中形成2个压应力集中区和1个拉应力集中区,其中,最大和第2压应力集中区分别出现在垫板端和内锚固段外端锚孔附近,而拉应力集中区出现在内锚固段锚孔附近。即锚杆预应力所形成的压缩带主要集中在未锚固段围岩中,而锚固段围岩中会形成不利的拉应力区,设计中应对此特别关注,避免产生较大拉应力量值区域的贯通。

2)锚固长度在一定范围内变化时,应力极值基本不发生改变,仅第2压应力峰值和拉应力峰值随锚固长度的变化发生偏移,第2压应力峰值始终出现在对应未锚固段与锚固段分界面处,而拉应力峰值则出现在锚固段靠近未锚固段一侧。随锚固长度增加,压应力区明显减小,当锚固长度增大到全长锚固时,仅在垫板端附近极小范围内形成压应力区,但拉应力量值存在明显减小,故实际工程的预应力施加阶段,在满足拉拔力需求的前提下不应追求过长锚固段。

3)越靠近洞壁处,靠近锚杆处应力集中越明显,而随远离洞壁径向应力趋于均匀。不同预应力大小作用下锚间σ3分布规律具有高度一致性,均随r/l先增大后减小,而量值随预应力量值增大而呈线性增加。群锚预应力形成的连续压缩带厚度随间距减小明显增大,但随长度增大变化不明显。同时,短锚杆更易在杆长范围内形成连续压缩带,而长锚杆无法在整个杆长范围围岩内形成压缩带,其应力扩散效果有限,故在参数设计中不应一味增加锚杆长度。

4)基于对所施加预应力利用率的考虑,可将p′×(Fp/(a·b))作为判定压缩带范围的阈值,即认为径向应力超过p′×(Fp/(a·b))范围为预应力有效压应力区。可通过比较不同参数预应力锚固系统所形成的围岩有效压应力区范围,进行预应力主动支护锚固系统关键参数设计。

由于本文重点在于考虑预应力锚杆形成的围岩压缩带内径向应力分布规律,对内锚固段接触未予以考虑,故该部分研究有待进一步开展。