两端自由椭圆形管段模型波浪荷载下截面关键点加速度的试验研究

王 方, 李 科, 丁 浩, 李鹏辉, 何 田, 黄 博, 3, 程 亮, *

(1. 招商局重庆交通科研设计院有限公司, 重庆 400067; 2. 重庆交通大学土木工程学院, 重庆 400074;3. 重庆交通大学 山地桥梁与隧道工程国家重点实验室, 重庆 400074)

0 引言

随着沟槽发育的复杂地形逐渐成为水下隧道的建设条件,传统工法面临着愈加严峻的挑战[1]。悬浮隧道作为一种全封闭新型结构[2],依靠浮力和锚索张力保持动力平衡从而跨越海峡海湾,其凭借自身独特优点,成为21世纪最具有竞争力的跨海结构之一[3]。然而至今还没有实际应用工程,原因之一为所受外部荷载种类繁多,动力特性复杂[4]。因此,开展波浪场作用下悬浮隧道管体的加速度特性研究,对早日实现悬浮隧道工程应用具有实际意义。

国内外针对悬浮隧道动力响应问题已开展了大量深入研究,并取得了重大进展。例如: 阳志文等[5]利用波流水槽构建悬浮隧道纵向截断模型试验,分析了波浪作用对悬浮隧道运动响应的影响,获得了管体结构的垂向及横向运动响应特性;李勤熙等[6]、Li等[7]、蒋树屏等[8]通过1∶80的物理模型试验,开展了随机波浪作用下的水中悬浮隧道力学模型试验;Luo等[9]建立理论水动力模型,研究了缆长、浮力重比、周期、波陡、水深等参数对波浪荷载作用下悬浮隧道动力响应的影响;Sun等[10]将受拉支腿假设为端铰接的非线性梁模型,采用 Galerkin法和 Runge-Kutta法求解,结果表明悬浮隧道张力腿的参数振动响应与末端激励的幅值、频率有关;Chen等[11]提出了一种研究悬浮隧道管索系统非线性动力响应的理论方法,揭示了在参数激励和水动力激励联合作用下悬浮隧道的动态特性;Yang等[12]介绍了波浪与悬浮隧道相互作用过程中悬浮隧道运动的试验观测,并深入分析了波高、波周期、潜深、浮力重比、系泊线角等控制参数对悬浮隧道运动的影响;Drost[13]开展波流作用下淹没矩形圆柱体的流体动力学和运动学试验研究,分析了不同系泊角度和淹没深度组合下加速度动力响应;Deng等[14]通过开展自震荡模型试验,研究了双管悬浮隧道模型的横流涡激振动特性;Oh等[15]通过二维波浪水槽物理试验,研究了波浪作用下悬浮隧道动力响应。

虽然现有研究取得了丰富的实质性成果,但也存在着许多不足: 目前所研究悬浮隧道的动力响应大多比较宽泛,较少学者针对悬浮隧道加速度特性开展具体深入的研究,且研究方法主要是理论推导和数值模拟,仅有少量学者开展单因素、小比尺的相似模型试验。本文在现有研究基础上设计定制大尺度试验模型,开展两端自由椭圆形管段模型试验,分析讨论规则波浪荷载作用下管体加速度特性,以期完善悬浮隧道的动力响应理论。

1 模型试验设置

1.1 试验装置

本试验地点为招商局重庆交通科研设计院有限公司内部水下隧道实验室,实验室配备了大型波流水池、造波系统和室内大型可移动拖车等装备[16]。水池的尺寸为24 m×24 m×3 m(长×宽×深),满足大范围波流场的试验要求。造波系统主要由造波整列、伺服电机、造波机控制器和计算机控制系统构成,它可以模拟在0.5～2.0 s周期和2.5～20 cm波高内的规则线性波、不同谱型的随机波以及各类非线性波浪,且具有自动迭代功能。大型可移动拖车主要用于移动固定试验模型和设备。此外,水池末端设置了一定坡度的消波层,该消波层设计为网箱结构,外框使用铝合金型材,内填塑料盲沟板,主要用于减小波浪反射和吸收波浪能量。

1.2 试验模型与测量仪器

1.2.1 试验模型

基于琼州海峡跨海通道背景和前人的研究[17-18],本试验选择具有代表性的椭圆形断面,并根据几何形状采用双向6车道交通方案。在满足JTJ/T 234—2001《波浪模型试验规程》[19]和Froude相似准则条件下,根据断面结构尺寸、水深、波浪等诸多要素以及水池和造波系统的性能指标,模型缩尺选定为60。浮重比为1.3∶1,主要为管节模型的重量,缆绳重量相对较小,可忽略不计,剩余浮力由锚索系统来平衡。模型设计为双管节,管道边界设置为两端自由,截面的长短轴为0.75 m × 0.317 m。为了避免模型在荷载作用下发生结构破坏,模型壁厚取8 mm,尺寸误差均控制在±0.5 mm。试验模型主要参数如表1所示。采用亚克力模型制作内部隔板,用于加强模型整体抗变形能力。模型和仪器安装布置如图 1所示。

1.2.2 试验仪器

本试验采用加速度传感器测量管体的加速度情况,可在水下采集管体加速度时程信息,最大量程和精度分别为2.0 g和0.3%,采样率高达4 kHz,误差为∠±0.1%F.S,能够对管体的微小反应进行准确捕捉。加速度传感器通过防水胶粘贴在管体端部中心正上方,并通过内部的水准校订装置控制方向,保证加速度传感器Z方向与重力加速度方向相同,Y方向与波浪传播方向相向,X方向与管节长度方向相同。连接线用防水胶带与管体紧密粘贴,且摆放与加速度传感器Y方向一致,避免线缆对波浪传播产生影响,从而影响试验的准确性。

1.2.3 设置安装

首先将水池水位放至指定深度,在放置结构物前,先进行造波系统调试,验证试验波浪的准确性。在波浪荷载调试完成后,随即开展正式试验,模型安装在波流水池中间,距离造波推板约12 m,以保证波浪充分传播和发展;距离消波层约14 m,防止反射波的影响,配重组装和传感器粘结均完成的模型由吊车吊装到安放位置,接着进行防水检测和调试。通过水密性测试后,按照图 1(c)方式连接锚索,模型两侧各布置4根锚索,采用预装的金属环连接装置连接;锚索与模型连接后,另一端穿过水池底部滑轮装置,滑轮底部预留一定的空间,保证锚索在拉应力作用下绕滑轮平稳滑动。锚索通过滑轮后,与预装的拉力传感器采用不锈钢夹头连接,每根锚索用2个不锈钢夹头紧固,防止锚索滑动,确保试验过程中模型固定可靠、振动影响可控。水池水位增加到1.8 m,其他装置架设完成后,放水至预定水深2.2 m,最后确保模型悬浮在水下0.4 m处。

1.3 试验参数与数据采集

根据我国东海岸海洋观测站的波浪参数统计资料[20],选取试验波浪参数如下: 试验时水池水深d保持2.2 m不变,入射波高H为0.05 ～ 0.10 m,波周期T为0.8 ～ 1.1 s,波浪传播方向始终垂直于悬浮隧道模型截面。为了减少测量结果的重复误差,保证试验结果的可靠性,每组试验一般重复3次,取3次试验的平均值。

试验波浪由计算机控制推板产生,波浪参数会受到多种因素的影响,正式试验前在造波系统输入参数进行调试,以验证生成波浪的准确性。使用测波仪测量无模型中心位置处的入射波高,选取采集的多周期规则波面时程与线性波理论解析进行对比,结果如图2所示。可以看出: 1)不同工况中波浪的传播均较稳定,2种规则波浪的变化趋势一致; 2)试验波面与理论解吻合非常好,误差在3%以内,这表明试验设备能生成准确稳定的规则波。

(a) H=0.06 m,T=0.86 s (b) H=0.07 m,T=0.96 s

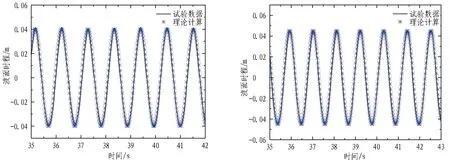
(c) H=0.08 m,T=1.06 s (d) H=0.09 m,T=1.1 s

2 管体加速度时程

2.1 波高对加速度时程影响

选取周期为0.9 s,波高分别为0.05、0.06、0.07、0.08、0.09、0.10 m的6种工况,分析波高对管体的X、Y、Z3个方向加速度时程的影响。其中,X方向为管体长度方向(简称为管体纵向),Y方向为波浪传播方向(简称为管体横向),Z方向与重力加速度方向相同(简称为管体竖向)。不同波高下管体加速度时程曲线如图 3所示。

由图 3可以看出: 1)当波高较小(小于0.08 m)时,管体的纵向加速度相应较小,在1个波浪周期内近似呈先增大后减小的变化规律,且与波浪作用有较大的相关性。这主要是波浪的反射以及波浪与结构的相互作用引起的。2)横向加速度远大于纵向加速度。造成这种现象主要是因为横向为规则波浪的传播方向,水质点的横向运动带动了管体的横向运动。3)横向加速度在波高小于0.07 m时呈现不规律的变化趋势,甚至出现了双峰及多峰现象,并且正向加速度持续时间要远大于负向加速度持续时间。产生该现象主要原因是波浪在传播到管体附近时,前一个波浪带动水体作用于结构物,会产生相应的反射,其反射波与下一个波浪相互作用,波浪与反射波的相互作用以及波浪与结构物的相互作用共同导致了多峰的现象,这为典型的非线性变化趋势。随着波高的持续增加,横向加速度逐渐发展为单峰变化趋势。4)竖向加速度在小波高时存在着较为复杂且无规律变化。其变化规律为1个波浪周期出现2次峰值,随着波高的增加,第2个峰值逐渐减小,直至消失。5)当波高为0.10 m时,竖向加速度呈现非线性较强的周期变化,在加速度正向变化较为剧烈,而在负向变化较为缓慢。

(c) 波高0.07 m (d) 波高0.08 m

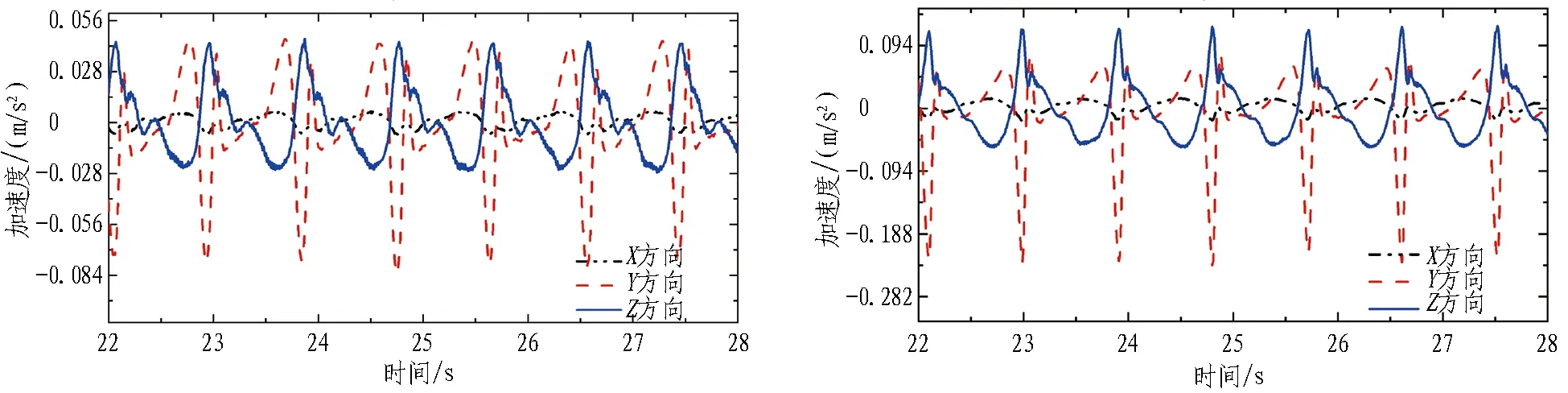
(e) 波高0.09 m (f) 波高0.10 m

在周期一定的情况下,波高从0.05 m增大到0.10 m,可以发现3个方向的管体加速度均呈现增大的变化趋势。产生这种现象的原因是因为波高越大,水深处水质点受波浪影响越大,水质点能量越多,导致加速度越大。随着波高的增加,管体横向加速度时程峰值处从原有的高频转向低频,且加速度峰值有较为明显的非线性增长趋势;竖向加速度时程随着波高的增加呈现周期性的变化规律。

2.2 周期对加速度时程影响

选取波高为0.10 m,周期分别为0.8、0.9、1.0、1.1 s的4种工况,分析波浪周期对管体的X、Y、Z3个方向加速度时程的影响。不同周期下管体加速度时程曲线如图 4所示。

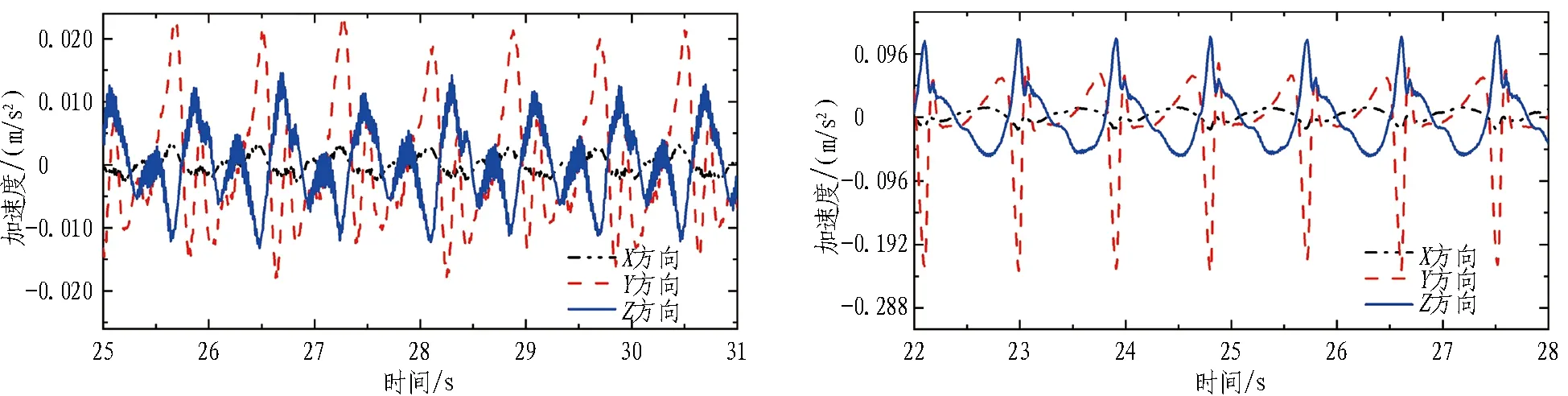
(a) 周期 0.8 s (b) 周期 0.9 s

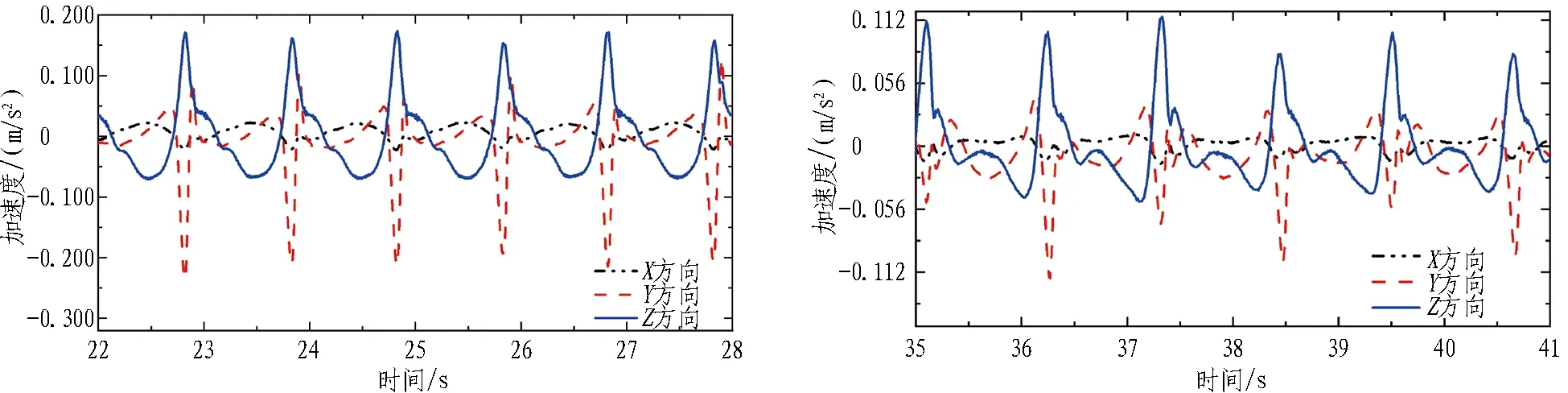
(c) 周期 1.0 s (d) 周期 1.1 s

由图 4可以看出: 1)周期由0.8 s增加到0.9 s时,管体横向和竖向加速度时程发生了较大变化,纵向加速度变化较小,其变化规律也未有明显变化。2)横向加速度逐渐发展为单峰变化,在一个波周期内先增加到峰值,后迅速减小至最小值,继而迅速上升至峰值,并且横向加速度由正向加速度较大逐渐转变为负向加速度远远大于正向加速度。这表明管体在短时间内速度变化较大,在大波高工况下横向负加速度的作用不可忽视。3)竖向加速度呈现非线性较强的周期变化,在正向变化较为剧烈,在负向变化较为缓慢。4)当周期T为1.0 s时,纵向加速度呈现较为规则的变化趋势,横向负加速度远大于正加速度,竖向加速度也呈现较为显著的非线性周期变化。虽然较大波高会导致波陡的增大进而引起波浪破碎等现象,但同样波浪的周期性会使竖向加速度更具有周期性和规律性,在锚索的作用下,管体向上运动会受到约束,向下运动会更加缓和。5)当波浪周期为1.1 s时,可以观察到管体3个方向的加速度变化规律的非线性有所减弱。其中,纵向加速度呈现双峰波动,且基本保持正向加速度状态;横向加速度的非线性也同样有所减弱,主要在峰值处波动减弱;竖向加速度呈现了较为明显的单峰状态。

在波高一定的情况下,管体的加速度时程在小周期的波浪作用下呈现出高频多峰特征,主要是由于小周期时波浪的波长较小,导致在波浪高度相同的情况下波陡值增大,进而引发波浪破碎现象;同时较小波长的波浪作用在结构上,将导致模型产生较为高频的运动。随着波浪周期的增大,波长也相应增加,使得波陡降低,减弱波浪破碎和能量耗散,同时波长与结构尺寸比值的变化也导致模型的动态响应有所区别。

2.3 加速度傅里叶变换频域

为了更全面地了解波浪作用下管体加速度的频域特性,对模型管体纵向、横向、竖向加速度进行傅里叶变换。

不同波高下管体加速度的傅里叶变换频谱对比如图 5所示。可以看出: 1)在波浪荷载作用下,当波高较小时,管体的纵向加速度频域显示出较为明显的低频现象(即频率1.113～2.225 Hz),出现了2个峰值,在约1.113 Hz频率处的最大值为0.000 7 m/s2。2)管体的横向加速度频域具有较宽的频率区和更高的幅值,并表现出更多的随机特性,出现多个峰值,其能量集中在频率1.113～8.901 Hz,同样在频率约1.113 Hz时的最大值为0.006 5 m/s2。3)管体的竖向加速度频域现象和横向加速度相似,同样表现出较多的随机性,出现多个峰值,不同的是在约2.225 Hz频率处的最大值为0.006 2 m/s2。随着波高的增大,3个加速度频率区均发生了较大的变化。4)纵向加速度仍显示出明显的低频现象,但仅出现唯一峰值,同样在约为1.113 Hz频率处出现最大值,但最大值增大为0.011 2 m/s2。5)横向加速度频率同样具有较宽的频率区和更高的幅值,且出现多个峰值。这再次说明了非线性变化现象,主要原因是波浪与反射波的相互作用以及波浪与结构物的相互作用。各个峰值相差不大,在频率约为2.225 Hz时的最大值为0.040 2 m/s2。6)竖向加速度频域变化最大,能量集中在频率1.113～4.451 Hz。频率区变窄,在低频区约1.113 Hz处的最大值为0.057 0 m/s2,幅值约增大了9倍。

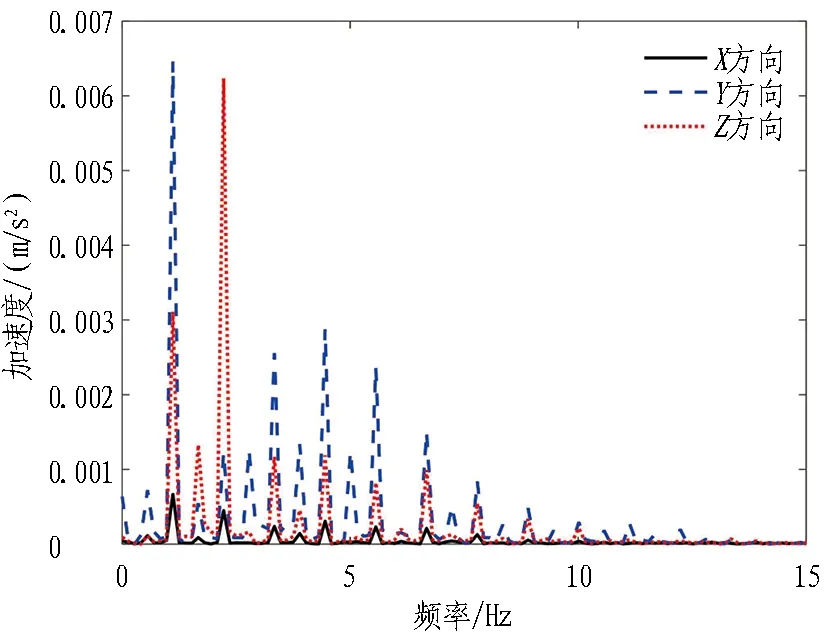
(a) 波高0.05 m

(b) 波高0.10 m

不同周期下管体加速度的傅里叶变换频谱对比如图 6所示。可以看出: 1)在波浪荷载作用下,当波高一定时,随着周期由0.8 s增大为1.1 s,纵向加速度仍处于低频率区。2)当小周期时,在频率约1.252 Hz时的最大值为0.001 7 m/s2。3)当较大周期时,在频率约0.910 1 Hz时的最大值为0.006 0 m/s2,幅值增大了3倍。4)横向加速度的频率区变宽,其能量集区由频率为1.252～6.260 Hz变为0～8.646 Hz,并表现出更多的随机性,由3个峰值增加为多个峰值。5)周期为1.1 s时,横向加速度具有更高的幅值,幅值最大值由0.010 2 m/s2增大为0.019 8 m/s2。6)竖向加速度频率具有更宽的频率区和更高的幅值,同样表现出更多的随机特性,出现了3个幅值相同的峰值,在频率约为0.910 Hz和1.820 Hz处的最大值为0.029 8 m/s2。7)在大周期条件下,其能量集中区域为0.910～6.371 Hz。

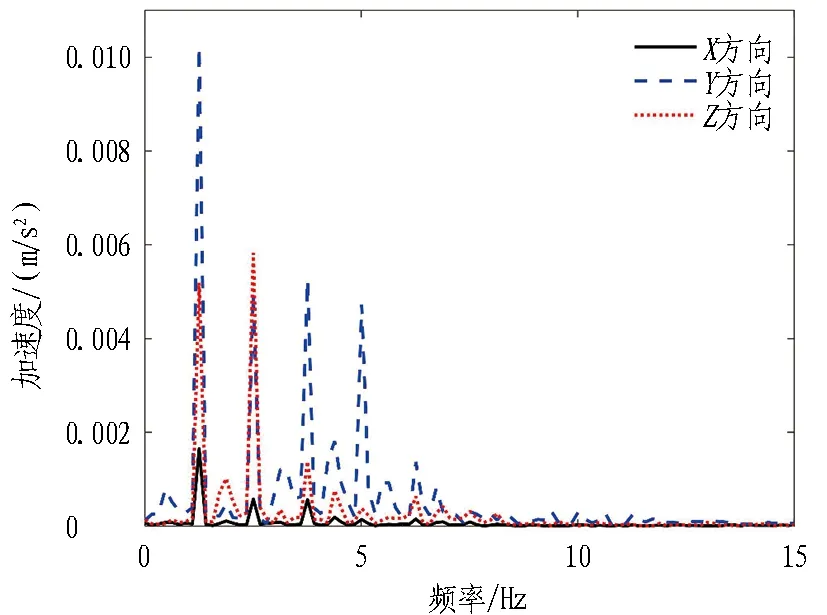
(a) 周期0.8 s

(b) 周期1.1 s

3 管体加速度极值

通过对模型管体加速度的时程变化分析,可以较为明显地看出波浪作用下加速度的非线性变化情况。为进一步探明波高和周期对模型管体加速度的影响情况,下文针对模型管体加速度最大值和最小值的变化情况展开讨论。

3.1 波高对加速度极值影响

选取周期为1.0 s,波高分别为0.05、0.06、0.07、0.08、0.09、0.10 m的6种工况,分析波高对管体的X、Y、Z3个方向加速度极值的影响。不同波高下模型加速度极值变化如图 7所示。

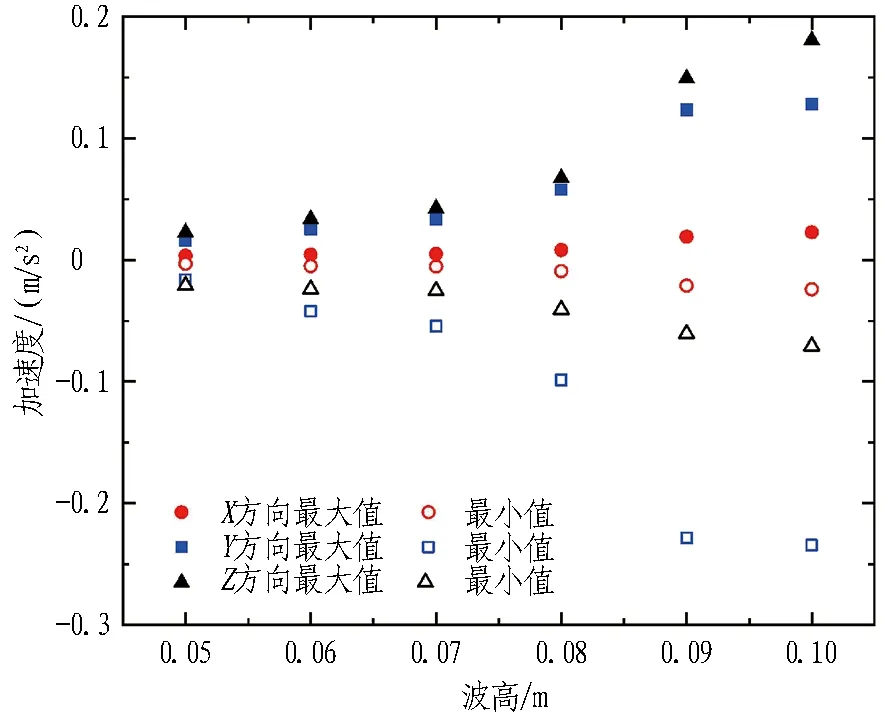
图7 不同波高下模型加速度极值变化图

由图 7可以看出: 1)随着波高的增大,管体的纵向加速度呈现较大程度的波动。造成该现象的原因为纵向加速度主要由波浪的反射以及波浪与结构物的相互作用造成,其绝对值一般较小,变化也较为不稳定,导致了加速度极值不稳定现象。2)纵向加速度随波高的变化呈现较为对称的分布,即最大值和最小值的绝对值近乎一致。这种现象说明在反射波浪以及波浪与结构的相互作用下,模型纵向呈现对称的振动响应。3)横向加速度最大值和最小值均随着波高的增加而增大。在波高小于0.08 m时,横向加速度的增长趋势较为线性,而当波高达到0.09 m时,横向加速度最大值急剧增大,最小值急剧减小,并且随着波高的继续增大,横向加速度的变化幅度较小。造成该现象的主要原因可能是大周期波浪下,随着波陡的降低,一方面导致了波浪在大波高处不易发生破碎,造成能量损失;另一方面是波长与结构尺寸之比的增加也会导致波高对结构响应的影响加大。该现象也发生在管体竖向加速度的变化规律上。

3.2 周期对加速度极值影响

选取波高0.10 m,周期分别为0.8、0.9、1.0、1.1 s的4种工况,分析波浪周期对管体的X、Y、Z3个方向加速度极值影响。不同周期下模型加速度极值变化如图8所示。

由图 8可以看出: 1)随着周期的增大,管体纵向、横向和竖向加速度最大值均呈现先增大后减小的趋势,最小值也均呈现先减小后增大的趋势。2)当周期小于1.0 s,管体纵向、横向和竖向加速度呈现近似线性变化趋势。3)周期为1.0 s,管体纵向、横向和竖向加速度达到峰值。4)当周期增长到1.1 s时,可以发现管体纵向、横向和竖向加速度呈现最大值减小、最小值增大的变化趋势。这种现象表明,随着波浪周期的增大,波浪对模型动力响应的影响先增大后减小,该现象和波长与结构横向尺寸比值相关,当波长与结构横向尺寸之比达到一定值时,波浪对结构物的动力响应影响最大。

4 结论与建议

本文基于模型试验开展在波浪荷载作用下两端自由椭圆形管段动力响应研究,分析讨论波高、周期参数对模型管体的加速度时程变化和极值大小的影响,主要结论与建议如下:

1)当周期一定时,模型管体纵向、横向、竖向3个方向的加速度均随着波高的增大而增大。当波高逐渐增大时,纵向加速度变化较小,最大值呈现较大程度的波动,最小值变化较为稳定,呈现持续减小的趋势;横向加速度时程峰值处从原有的高频转向低频,且加速度峰值有较为明显的非线性增长趋势;竖向加速度随着波高的增加呈现多周期的变化规律,在一个波周期范围内,竖向加速度2个周期的峰值差距呈现先减小后增大的趋势,且最小值符合线性增长的趋势,最大值增长趋势与横向加速度相似,但在大波高时增长幅度有所下降。

2)当波高一定时,模型管体的加速度时程在小周期的波浪作用下呈现出高频多峰趋势,随周期呈现了非线性的变化规律,竖向加速度的规律性较为显著,特别是正向加速度持续时间有明显增长。随着周期的增大,管体的纵向、横向、竖向加速度极值大小均呈现先增大后减小的趋势。

3)本文只研究了一种环境荷载,不够全面,对于其他种类荷载作用下两端自由椭圆形管段的动力响应分析有待于进一步的研究。

4)本文试验模型边界设置为自由端,未采用节段刚度与原悬浮隧道约束及刚度等效的方式进行模拟及试验,未来可针对此方向进一步开展研究。