基于表面波纹特征的PIV 明渠表面流速测量方法研究

王 磊，朱 威，杨慧慧

(1.国能江苏电力工程技术有限公司，江苏 镇江 212006；2.东南大学能源与环境学院，江苏 南京 210096)

我国是世界上洪涝灾害频繁、严重的国家之一，洪水灾害不仅范围广、发生频繁、突发性强，而且会造成极大的损失。据统计，洪水灾害造成的经济损失和人员伤亡，在各种自然灾害中位居第一。自然河流的水文监测，特别是雨季流速场及河道流量等测量数据的获取对于洪水应急预防具有重要意义。

目前，我国河流、渠道流速及流量的测定主要采用接触式测流技术，最为常用的方法为转子式流速仪法[1]、超声波时差法[2]和多普勒ADCP 法[3-4]。转子式流速仪存在机械惯性、响应速度慢等缺点，无法测量快速变化的湍流，流量较大时无法入水测量，并且需要定期检定和维护，运维成本较高。超声波时差法使用的超声波流量计对水质要求较高，仪器必须工作于清水或仅有少量漂浮物的水域中，在浑浊的水中或在测量狭窄的渠道时精度较差。多普勒ADCP 法的主要缺点是必须进行船载测量，需要人工操作，在测量泥沙或杂质含量较高的水质时准确度较差，且对于宽度较小的渠道或流量较大时无法进行测量。总体而言，天然河流复杂的紊动特性，加之恶劣的现场环境大大增加了水文监测的难度，导致传统接触式测流方法在河道水流监测中面临着诸多挑战。

近年来，非接触式河渠水流监测技术在传感器及嵌入式技术的推动下取得了长足进步，基于声学[4-5]、光学[6]、雷达[7]及图像[8-9]的测流仪器显著提高了水文监测的准确性与时效性。特别是以粒子图像测速(Particle Image Velocimetry，PIV)为代表的图像法瞬时全场流速测量技术，因其可获得全流场的瞬时流动信息及较高的测量精度，满足对大尺度、高雷诺数、复杂边界流动的研究需求，导致该技术在高洪期及浅水低流速等极端现场条件下河道水流监测中的应用潜力得到了广泛关注。在河渠流速测算领域中应用改进后的PIV 算法，能有效避免传统接触式测量方法测量历时久、测量效率低的弱点，实现高精度持续测量，具有重要的工程意义。

1 PIV 算法原理分析

PIV 测速法[10-16]是上世纪70 年代末发展起来的一种瞬态、多点、非接触式的流体测速方法，其主要核心为对示踪粒子(本论文中视河面水波纹为示踪粒子)在已知短时间间隔的位移进行分析，间接提取流场的瞬态速度分布。示踪粒子在流场中的二维速度可以表示为:

式中:，vx、vy为该粒子沿x、y方向的瞬时速度，Δt为测量的间隔时间为沿x、y方向的平均速度。当Δt足够小时的大小即可精确地反映该粒子瞬时速度vx、vy。

实际应用中，常用高清CCD 相机以固定姿态对流场中待测区域粒子进行连续拍照。由于整个待测区域含有大量粒子，很难从不同底片中分辨出同一粒子，因此无法获取所需位移矢量信息。通过图像处理的方法可将待测区域分为若干子区域(简称相关窗口)，采用相关窗口的互相关算法可求得窗口内粒子的位移矢量。t时刻粒子位于(x，y)处的窗口(当前窗口1)，t+Δt时刻粒子所处的窗口可利用当前窗口1 和搜寻窗口(窗口2，3，…)进行互相关运算获得。最大互相关峰值位置处窗口，即t+Δt时刻粒子所处的窗口。

2 算法改进及全局标定法

2.1 算法改进

经典的互相关算法往往运算量大、耗时长，为了提高运算效率，本论文采用傅里叶(FFT)变换，以多帧连续互相关和窗口迭代缩小的方法，来实现互相关函数的运算[17]，使得结果更加贴合实际、分辨率更高。图1 为基于FFT 的互相关算法流程图。

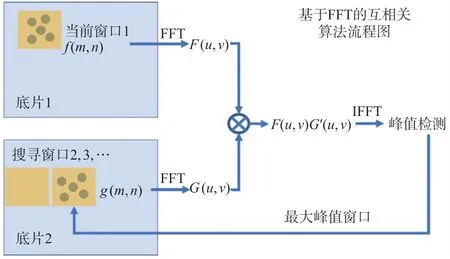
图1 基于FFT 的互相关算法流程图

分别对第一帧图像和第二帧图像的相关窗口进行进行快速傅里叶变换，得到F(u，v)和G(u，v)，然后对两频域变换结果做卷积得到相关窗口内粒子像的能量谱，其中G＇(u，v)是G(u，v)的复共轭变换(FFT＇)；最后对频率空间的能谱进行傅里叶逆变换IFFT，得到相关窗口的互相关函数(3)。对相关平面进行峰值检测找到最大峰值对应窗口便可获得位移矢量信息，代入式(1)及式(2)计算后得到二维像素速度场分布。

2.2 全局标定法实现流速场修正

2.1 节所提出的改进算法可对拍摄图像进行快速处理分析，得到空间分辨率较高的二维像素速度场信息。在本论文的河流流速测算应用场景中，需要对河道固定区域进行流速流量全面测量，由于现场环境的复杂性以及拍摄区域尺度较大，为保证图片的稳定性和清晰度，往往需要将相机以一定角度架设在河岸俯拍河面。透视作用将导致拍摄得到的图片“远小近大”，图片尺寸一致性差。如图2 所示，棋盘格正视图(横线上方)内格子尺寸均匀等大，透视图(横线下方)尺寸变化较大。后续流速场的修正需要考虑该透视因素，利用标定实现像素速度场到真实空间速度场的尺度转换。

图2 棋盘格正视(横线上方)及透视(横线下方)效果比较图

本论文提出全局标定法，分为横向(x方向)插值标定以及纵向(y方向)区域平均标定。相机在现场确定拍摄姿态后，返回实验场地，以相同姿态完成标定，得到图像全局像素-实际尺寸转换关系。

横向插值标定:已知标定区域内两平行线的尺度转换关系，对其进行线性插值，即可得到全局横向转换尺寸。如图3 所示，实验室内地面正方形瓷砖尺寸一致性好，均为15 cm×15 cm，在直线1 与直线2 上截取相同数目瓷砖的像素尺寸(例如在直线1、2 上分别截取3 块瓷砖对应的像素尺寸，得到AB、CD)，计算得到该方向上像素尺寸与实际尺寸的尺度转换关系，对该尺度转换进行横向线性插值，即可得到该相机姿态下图像横向各像素与实际尺寸转换关系，如图4 所示。图4 中每条横线上两星点之间间距为该方向上每个瓷砖对应的像素尺寸，由上到下呈现增长趋势，与实际相符。

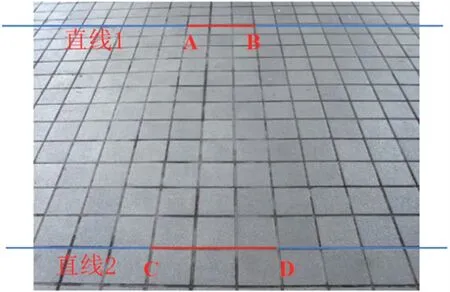
图3 实验室内标定地板瓷砖

图4 横向插值标定示意图

纵向区域平均标定:由图3 可知，由于在纵向不再满足横向的平行关系，因此很难实现纵向尺寸线性插值。为减小标定误差，主要将标定区域等分为多个子图，在每个子图上分别进行纵向标定。原则上，子图划分越多结果越精准。如图5 所示，将图3划分为4 个子图，对其进行以下操作:

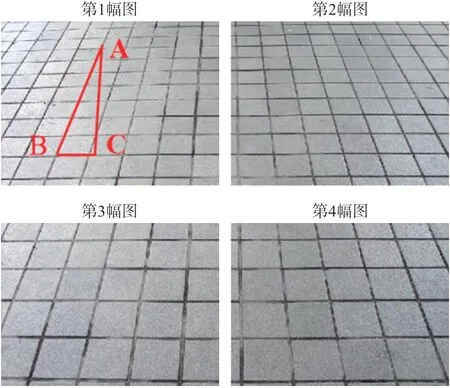
图5 纵向区域平均标定示意图

①在第i＝1 幅子图上，任意选取N个格子，连接两端格子顶点A、B(图中直线AB间N＝7，AB＝7×15 cm＝105 cm)；

②由横向标定可得到B点所在横线的横向尺度转换关系，带入BC的像素尺寸即可计算得到BC实际长度；

③通过勾股定理计算得到AB在纵向上投影尺寸和尺度转换关系。将该局部纵向尺度转换视为该区域的区域纵向尺度转换；

④对余下子图i＝2～4，重复步骤①～步骤③，即可得到全局范围内的纵向像素-实际尺寸转换关系。

3 实验平台搭建及测量

3.1 实验平台器材

实验平台由高清摄像机、伸缩三脚架、数显角度尺和PC 端搭建而成，如图6、图7 及表1 所示。调节伸缩三脚架高度和高清摄像机拍摄角度，拍摄河渠表面，将采集得到的视频信息上传至PC 端进行分析处理，最后得到场流速测算结果。

表1 流速场测量实验主要器材

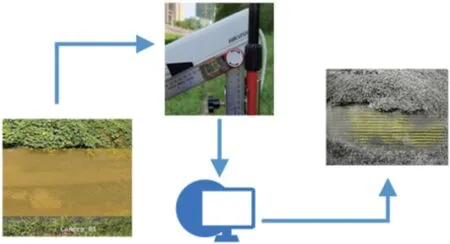
图6 实验平台搭建示意图

图7 实验器材

3.2 全局标定及流速测量

首先将相机及支架带到河岸，调节支架高度以及相机角度，确保相机拍摄区域河渠水流波纹清晰。用卷尺和数显角度尺记录相机离水面高度以及姿态角度，用于后续实验室全局标定。

其次进行参考水速的测量，在河岸固定两竹竿，如图8 所示，设置两杆间距L为标记物漂流距离(该实验中标记物为漂浮的树叶)，分别拍摄有标记物和无标记物两段视频。其中，有标记物视频记录标记物完整漂浮过杆过程，记树叶漂浮过杆用时为t，标记物的平均速度可由L/t得到，作为参考速度与PIV 计算无标记物视频所得速度进行比较。

图8 标记为拍摄与参考流速计算

4 实验结果分析

4.1 标定误差

全局横向标定误差:利用2.2 中横向插值标定的方法，将实验中摄像机所摄图像横向方向等分为20 段，得到各段像素与实际尺寸的转换关系，即尺度，如图9 所示。在每段方向上利用数据游标标记一个瓷砖的像素尺寸，将其代入“尺度×像素尺寸”得到计算尺寸，与实际尺寸进行比较，可以得到相对偏差，如表2 所示。利用横向插值标定的方法，全局平均相对误差为5.81%，标准偏差为3.53%。

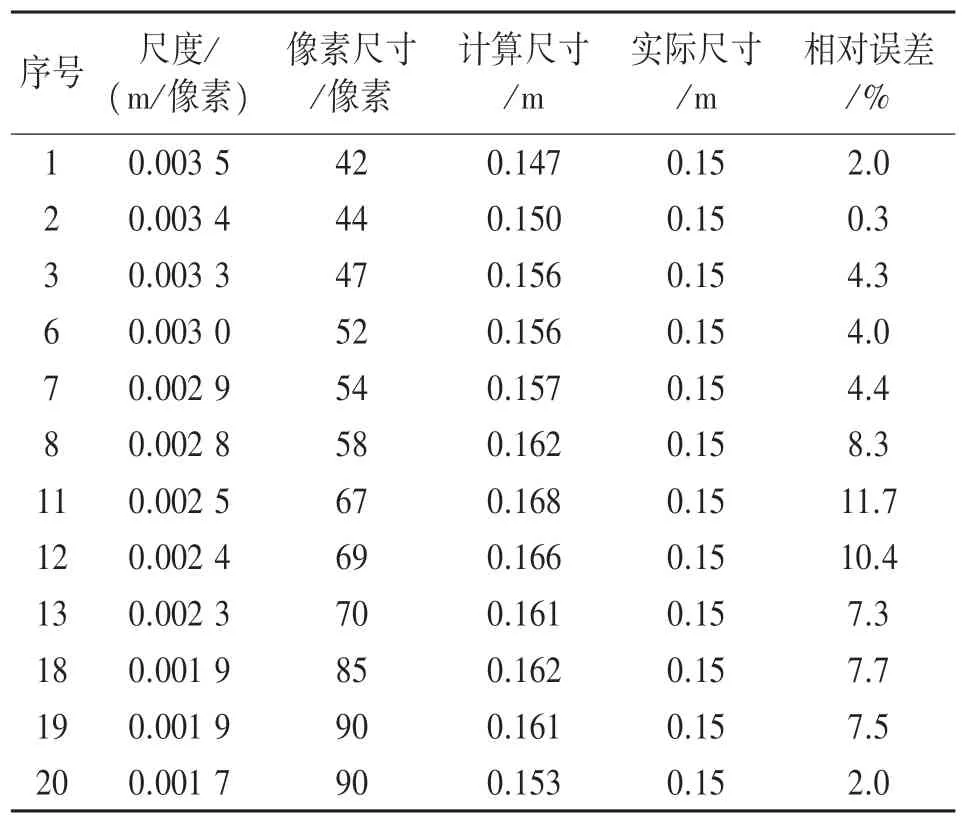
表2 流速场测量实验横向插值标定误差

图9 所摄图像横向各像素与实际尺寸的转换关系

全局纵向标定误差:利用2.2 中全局纵向标定的方法，将拍摄图像等分为多个子图，得到各子图内像素与实际尺寸的转换关系，即尺度。在各子图的纵向方向上利用数据游标标记一个瓷砖的像素尺寸，将其代入“尺度×像素尺寸”得到计算尺寸，与实际尺寸进行比较，可以得到相对偏差。为验证子图划分数与测量精度是否相关，将相机拍摄得到图像分别等分为4 子图和16 子图进行全局纵向标定。

对于4 子图的全局平均纵向标定如表3 所示，在同一子图内，取三个不同的区域(用a，b，c 表示)进行尺寸计算，与实际尺寸比较得到该区域的相对偏差。全局平均相对误差为8.03%，标准偏差为9.54%。

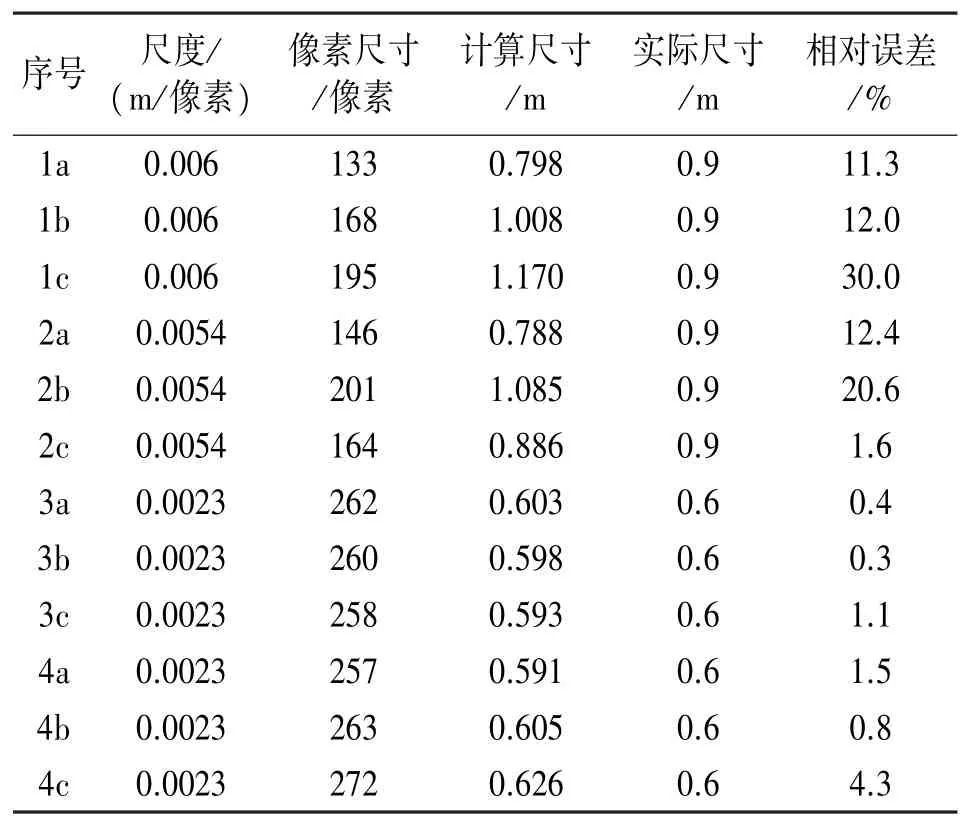
表3 流速场测量实验4 子图纵向标定误差

用相同的方法对16 子图进行全局平均纵向标定，其全局平均相对误差为5.07%，标准偏差为5.44%。

相较于4 子图，16 子图划分更精细，尺度转换更贴近局部真实情况，因此相对误差更小，标定效果更佳。在拍摄范围较广的区域内，横向插值标定与纵向平均标定仍可将标定相对误差控制在6%以内，准确度较高。

4.2 测量误差

沿河岸不同位置截取三段河道分别测量水流流速，按照3.2 中所述设定标记物及其漂流距离，结合漂流时间即可求得三段河道的参考水速，如表4所示。

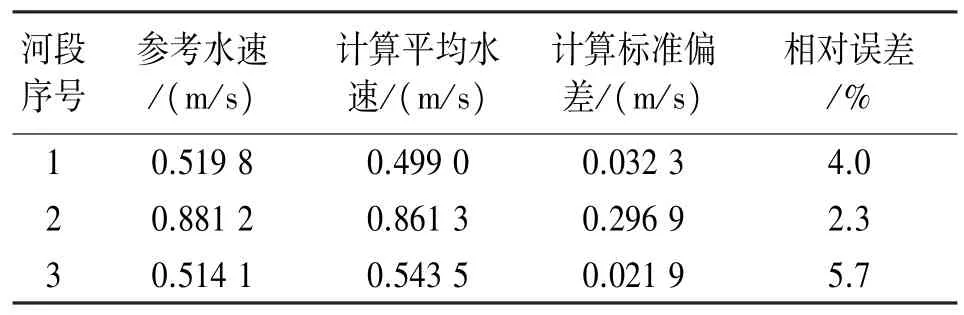
表4 流速场测量实验测量误差

用2.1 中改进的PIV 算法分别分析计算录制的视频，得到拍摄区域内全局流速场分布，如图10 所示。箭头方向代表水流流速方向，箭头尺寸大小和速度快慢呈正相关。

图10 改进后PIV 算法求得的流速场分布图

由表4 可知，三条河段计算得到的平均水速与参考水速间相对误差均保持在6%以内。三段河道相对误差平均值为4%，结果与实际较为贴近。

4.3 误差分析

标定误差与测量误差数值整体均在6%左右，但局部存在偏差，引起该偏差的潜在原因包括:

①相机拍摄存在畸变，例如水平线在拍摄图像边缘地带呈现向下弯曲趋势，而拍摄中心地带则保持水平。

②横向插值标定与纵向平均标定的精确度取决于横向插值数与子图分割数，即插值数与子图分割数越多，像素尺寸与实际尺寸的局部对应关系越精准。

5 结论

本文利用一种基于快速傅里叶变换的互相关改进算法，以多帧连续互相关和窗口迭代缩小的方法，来实现互相关函数的运算，有效地减少了互相关的重复计算量，提高了运行速度。实验结果表明，文章提出将测量监视图像与实际空间尺寸一一对应转换的全局标定法，结合改进后的算法，使得结果更加贴合实际、分辨率更高，可在河渠场流速测算中得到较好的应用。计算所得流速场速度与实际水流流速的相对误差可保证在6%以内。