基于混沌多项式的再入滑翔鲁棒轨迹凸优化
2023-11-21闫循良王培臣夏文杰王宽杨春伟
闫循良, 王培臣, 夏文杰, 王宽, 杨春伟
(1.西北工业大学 航天学院 陕西省空天飞行器设计重点实验室, 陕西 西安 710072;2.中国人民解放军96901部队,北京 100094)
轨迹优化设计技术是高超声速滑翔飞行器的关键技术之一,也是近年来研究的热点问题[1-3]。多种复杂约束和典型飞行任务条件给高超声速滑翔弹道优化设计带来了严峻挑战,这使得以直接法[3-4]为代表的数值优化方法成为了解决该问题的主要途径。其中,伪谱法以较少的计算量和较高的精度优势被普遍使用[3],但仍难以实现多约束复杂条件下的弹道快速生成,而凸优化方法[4]因具有多项式复杂度、收敛速度快等特点,已被广泛应用于高超声速等航空航天领域的轨迹优化任务[4-7]。然而,现有的高超声速轨迹优化研究大都未考虑不确定性的影响,即轨迹优化研究通常仅注重标称情况下轨迹性能提升,而未考虑真实情况下轨迹的鲁棒性和可靠性。因此,部分学者逐步将研究重点聚焦于不确定性量化传播技术[8-10]以及考虑参数不确定性的鲁棒轨迹优化方法[10-15]。
典型的不确定性量化及传播方法包括蒙特卡洛法(Monte Carlo,MC)、线性协方差分析法、无迹变换法以及混沌多项式展开法等[8-12],这些方法在不确定性量化传播及鲁棒优化中得到了较为广泛的应用。其中,混沌多项式(polynomial chaos,PC)方法将随机变量表示为随机正交多项式的加权求和,能够以较低的计算代价获得与MC法相当的精度[12]。鉴于PC与直接法的优势,诸多研究将二者结合,设计了基于嵌入式[10-11]与非嵌入式[12-15]的问题转化策略。Fisher等[10]首次基于嵌入式策略将随机最优控制问题转化为高维确定性问题,并采用配点法对该问题进行求解。Jiang等[13]则将非嵌入式策略与hp伪谱法相结合,解决了火星再入鲁棒轨迹优化设计问题。Wang等[11]提出了一种基于嵌入式策略与凸优化的鲁棒轨迹优化方法,并与基于高斯伪谱法的方法进行对比,证明了所提方法在精度相当的情况下,计算效率显著提高。杨奔等[15]则将非嵌入式策略与凸优化结合,提升了气动参数扰动下再入轨迹设计的可靠性。
基于PC和直接法的随机问题求解技术虽然已被逐步用于鲁棒轨迹优化,但仍存在计算效率低、通用性较差以及难于处理多维不确定性等问题,因而限制了其在复杂约束及强非线性鲁棒优化问题中的应用。此外,现有的公开成果亦存在未综合考虑轨迹鲁棒性和可靠性等不足。因此,本文提出了一种兼顾过程安全性与终端鲁棒性的再入滑翔轨迹优化设计方法,该方法主要包含两部分关键技术:①构建基于非嵌入式混沌多项式和高斯求积策略的不确定性量化传播模型,实现随机问题的转化;②设计基于序列凸优化的鲁棒轨迹快速优化求解策略及算法。最终,以X-33再入滑翔飞行为例进行仿真,验证了方法的有效性与快速收敛性。
1 轨迹优化问题描述
1.1 确定性再入轨迹优化建模
假设地球为旋转圆球,建立以无量纲能量e为自变量的三自由度再入滑翔无量纲运动方程[4]
(1)
式中,自变量为无量纲能量e=1/r-V2/2,无量纲状态量X=[r,θ,φ,γ,ψ]T;r为无量纲地心距,V为无量纲速度,θ为地心经度,φ为地心纬度,γ为当地速度倾角,ψ为航迹偏航角,υ为倾侧角,控制量取为攻角α和倾侧角υ,即u=[α,υ]T。
无量纲升力和阻力加速度L,D计算公式为
(2)
式中:m0为常值质量;Sref参考面积;Re为地球半径;升力及阻力系数CL,CD均为攻角α和马赫数Ma的函数;大气密度ρ采用指数模型ρ=ρ0e-βh进行计算;h为飞行高度。
攻角控制指令由预设剖面α=α(Ma)直接给出,故待设计控制量仅为倾侧角υ,且需要满足以下约束
υmin≤|υ|≤υmax
(3)
轨迹优化的边界条件包括初始状态约束和终端状态约束
(4)
式中:X0与Xf由具体任务给定;e0与ef分别为初始状态和终端状态对应的能量。
(5)
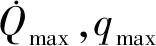
考虑到约束施加的便捷性,(5)式的过程约束可转化为地心距约束[4]
(6)
式中,lQ(e),lq(e),ln(e)可以通过反解(5)式得到。
定义L(e)=max{lQ(e),lq(e),ln(e)},(6)式可以表示为
r(e)≥L(e)
(7)
考虑飞行时间最短问题,即以飞行时间作为目标函数,则有
(8)
式中,τ为无量纲时间。
综合(1)、(3)、(4)、(7)、(8)式,即可构建以飞行时间最短作为优化目标的确定性再入轨迹优化问题P0。
1.2 不确定性因素建模
再入滑翔飞行所面临的不确定性主要包括再入初始状态,以及大气密度、气动力系数等动力学参数的不确定性,具体可建模描述为
(9)
且有
(10)
(11)
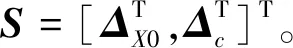
1.3 鲁棒再入轨迹优化问题描述
在问题P0中引入参数不确定性,则其状态量、目标函数、约束条件均为关于随机变量S的随机函数,为尽可能降低随机干扰对寻优结果的影响,即当存在不确定性时,预期轨迹离散度在统计意义上尽可能小,需要在目标函数、约束函数中引入随机量的统计矩,故可将问题P0转化为P1进行描述
(12)
式中:μ(·)和σ(·)分别表示随机函数(·)的均值和标准差;X(e,S)表示考虑随机干扰的状态量;kJ,kC为非负权重系数。
问题P1中,状态、约束、目标函数均为非线性随机函数,传统的确定性优化算法无法直接对其进行求解,一般需要引入不确定性量化传播技术计算相关统计量并处理随机动力学方程,进而采用高效优化算法求解转化所得到的高维确定性问题。
2 再入滑翔随机最优控制问题转化
本节将非嵌入式混沌多项式与高斯求解策略相结合,建立了不确定性量化传播模型,从而将再入滑翔鲁棒轨迹优化问题转化为高维状态空间中的等价确定性优化问题。以下给出算法原理及实现步骤。
2.1 非嵌入式混沌多项式算法原理
非嵌入式混沌多项式方法的核心思路在于对弹道模型的转换和样本点的选取,即通过随机变量取值空间上的积分点代替随机样本点,极大减少了模型的求解次数[16]。
首先,考虑形如(12)式的随机微分方程,其解X=X(e,S)采用以下混沌多项式进行逼近[12]
(13)
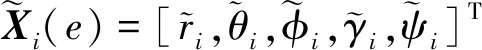
多项式展开的项数P+1可由(14)式确定
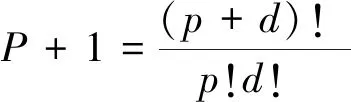
(14)
式中:p为多项式的阶数,其取值决定了多项式逼近的程度;d为随机向量S的维数。
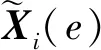
(15)
式中:Q=nd为随机空间的配点总数;n为S中单维随机变量的配点数;τm为配点sm对应的权重系数;X(e,sm)可在配点sm处积分确定性运动方程得到。
类似地,考虑(12)式中的目标函数J(X,e,S)、约束函数L(X,e,S)一般亦为状态X(e,S)的函数,故其混沌多项式展开形式为
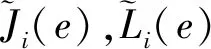
式中:Jm=J(X(e,sm),e,sm);Lm=L(X(e,sm),e,sm)可由确定性状态X(e,sm)求解得到。
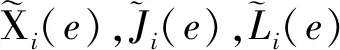
2.2 再入滑翔随机问题转化
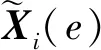
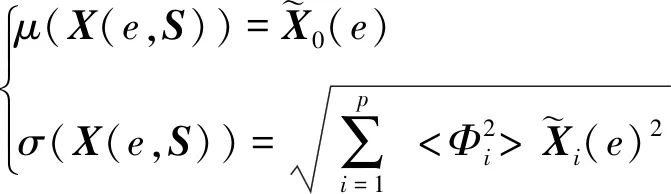
(20)
类似地,目标函数J(X,e,S)与约束函数L(X,e,S)的统计量亦可表征为相似形式。
结合2.1节的非嵌入式混沌多项式算法和上述统计量计算公式,可将问题P1转化为状态扩展的确定性轨迹优化问题P2,即
(21)
式中,Xm=[rm,θm,φm,γm,ψm]T。该问题为一高维确定性优化问题,其状态维数扩展为P1问题的Q倍。因此,下文采用凸优化方法对该高维确定性问题进行求解。
3 基于序列凸优化的轨迹优化求解
3.1 凸化处理
为避免抖振问题[4]出现,此处定义新的控制变量u=[u1,u2]T,有
u1=cosυ,u2=sinυ
(22)
且满足约束
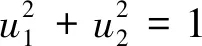
(23)
(24)
定义Dm=D(rm,e,sm),Lm=L(rm,e,sm),则有
(25)
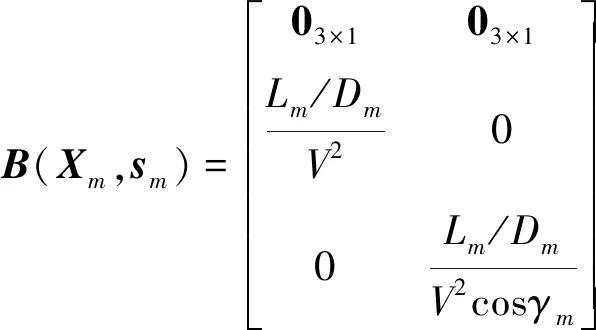
(26)
式中:fΩ(Xm,sm)为与地球自转相关的小量,且f0(Xm,sm)关于Xm是非线性的。以下采用逐次线性化方法,对相关非线性方程进行凸化处理。
1) 动力学方程凸化
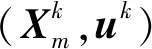
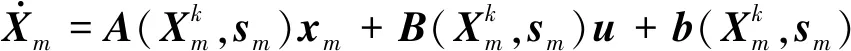
(27)
且有
(28)
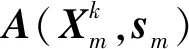
(29)
式中,δ表示信赖域半径,m=1,2,…,Q。
2) 目标函数凸化
为使班会的内容更为饱满,形式更为生动,有效实现主题,我尝试着将寓理式微型班会与体验式微型班会的结构模式相结合。下面我将从主题的导入、展开及深化三个方面来谈谈这堂课的环节设计:
(30)
定义a0=2m/(ReSrefCD(α,Ma,sm)V3),则
(31)
可得凸函数
(32)
此外,目标函数第二项为凸二次函数,故其整体即为凸函数。
3) 控制约束凸化
将(21)式中倾侧角幅值约束转化为对控制量u1的约束,即
cos(υmax)≤u1≤cos(υmin)
(33)
此外,利用松弛技术对(23)式的非凸附加约束进行凸化处理
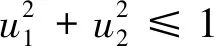
(34)
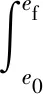
4) 过程约束凸化
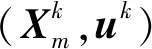
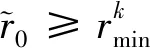
(35)
且有
(36)
至此,问题P2即转化为等价的高维确定性轨迹凸优化问题P3,限于篇幅,此处不再重复列出。
3.2 离散化处理
为了应用数值方法对凸化后的问题P3进行求解,需要对状态量和控制量进行离散化处理。将自变量变化域[e0,ef]等间距离散为N个间隔,自变量离散为[e0,e1,…,eN],状态量Xm离散为[Xm(0),Xm(1),…,Xm(N)],控制量离散为[u0,u1,…,uN]。
采用梯形法则对(27)式进行离散,可得
(37)

类似地,对问题P3的其他约束及目标函数进行离散化处理,得到
(38)
最终可以得到离散化的问题P4,可通过经典内点法求解,其优化变量包括每个离散点处的Q组状态量xm(h)和控制量uh,待优化变量数目为(5Q+2)N。
3.3 序列凸优化求解策略
问题P4将动力学约束线性化处理,故必然存在模型偏差,序列凸优化算法通过迭代求解P4问题对初始问题进行逼近,即利用外层迭代更新求解变量序列,内层求解问题P4,逐步逼近原问题P2的解,以保证凸优化解的收敛性和精度,即令
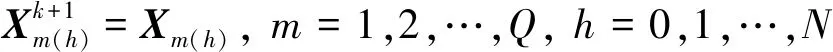
(39)
以相邻2次迭代的凸优化解对应的状态量最大偏差作为收敛准则,即
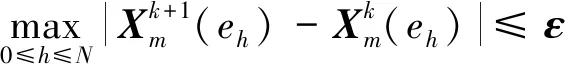
(40)
式中,收敛误差限定义为ε=[εr,εθ,εφ,εγ,εψ]T。
以下给出基于序列凸优化求解原最优控制问题P2的步骤和策略:
1) 根据随机向量S服从的分布确定配点sm和对应积分权重τm,其中m=1,2,…,Q;
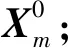
5) 判断(40)式是否成立,若成立,则算法结束;否则,令k=k+1,转入步骤3)。
4 仿真分析
4.1 仿真条件设置
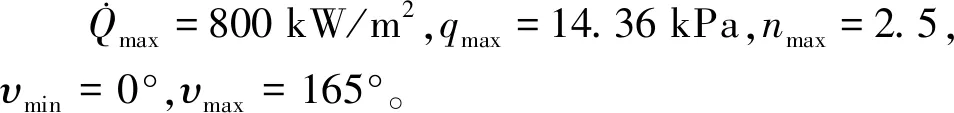
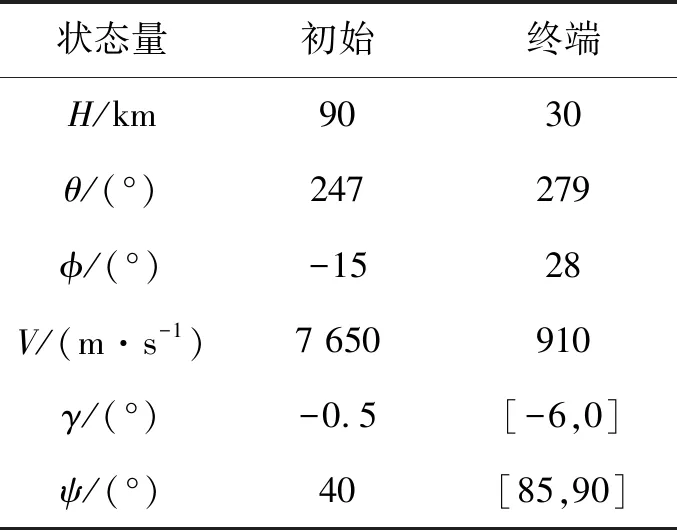
表1 边界条件取值
(41)
所有仿真均在搭载Intel Core i7-8700 3.20 GHz Intel处理器的台式机完成,仿真环境为MATLAB 2016b平台。基于自行开发的代码进行不确定性量化传播,同时基于CVX工具包进行轨迹优化算法开发,并调用SDPT3求解器求解凸优化子问题P4。
仿真中采用固定数目等距离散点,取值N=300,序列凸优化算法的信赖域半径和收敛误差限设置为:
(42)
4.2 确定性轨迹优化及不确定性量化传播仿真分析
首先,利用序列凸优化算法对问题P0进行仿真求解,得到标称条件下的再入滑翔轨迹优化结果,如图1所示。图1a)给出了速度-高度初始参考及优化结果曲线,可以看出,优化轨迹连续光滑,满足过程约束;由于性能指标为时间最短,故高度曲线始终处于下边界附近。由图1b)可知,优化结果满足过程约束要求,热流密度和过载曲线存在一定时间区间内达到约束峰值的情况。
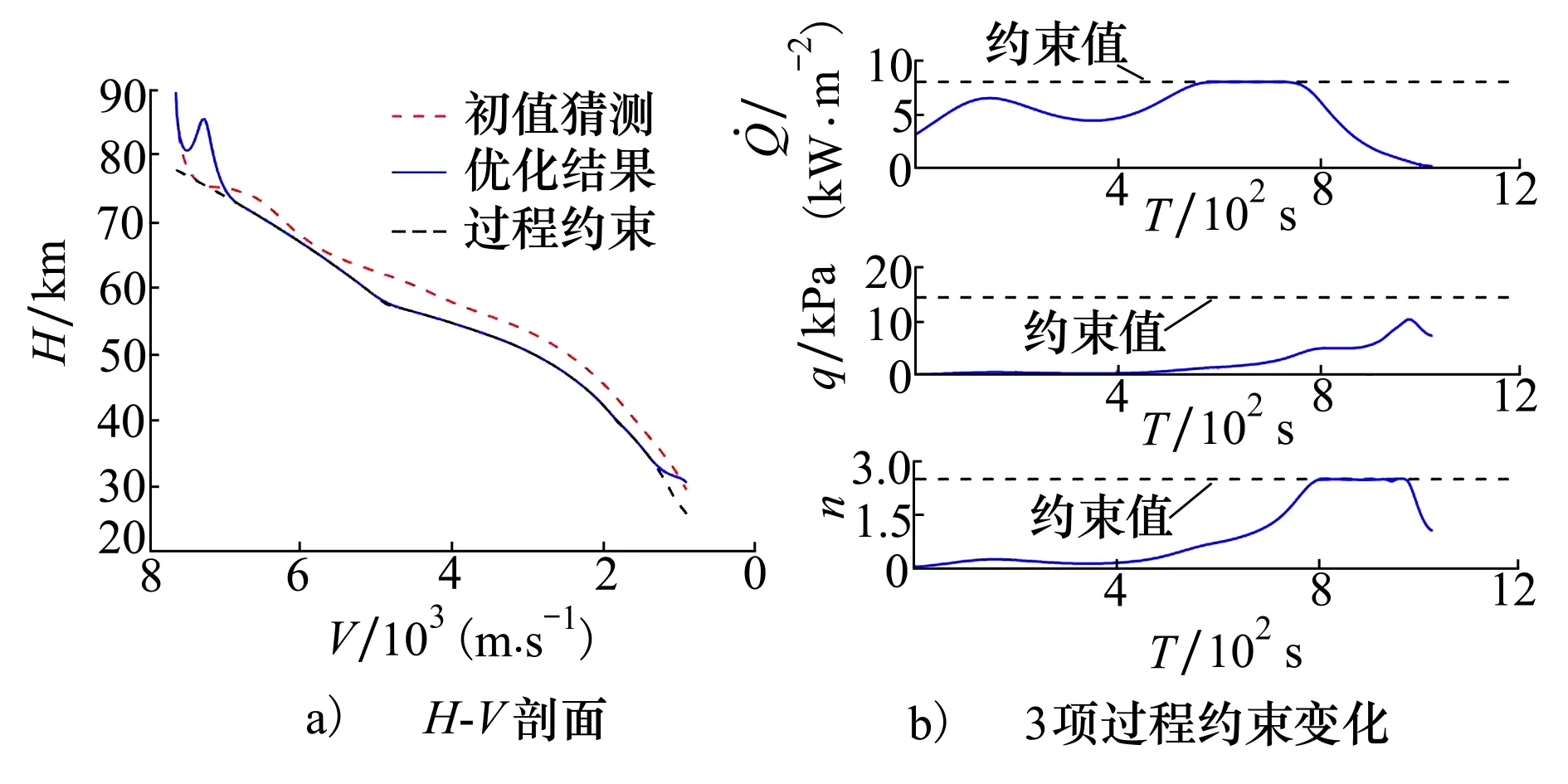
图1 标称情况下滑翔轨迹优化结果
以下基于标称条件下的优化结果分别开展蒙特卡罗打靶法(MC)与混沌多项式方法(PC)的不确定性传播量化仿真,以验证所提不确定量化方法的有效性。设定MC打靶次数为5 000次,所得结果如图2所示。由图2可知,再入飞行存在超出热流约束边界的情况,统计结果显示超出过程约束边界的概率达到了78.5%,可见,标称情况下的优化结果易受到参数不确定性的影响,从而出现终端精度下降和过程约束超限等问题,在实际飞行过程中,上述问题会显著增大任务失败的风险,因此,需要进一步开展考虑不确定性的鲁棒轨迹优化研究,以提高优化轨迹的抗干扰能力和可靠性。
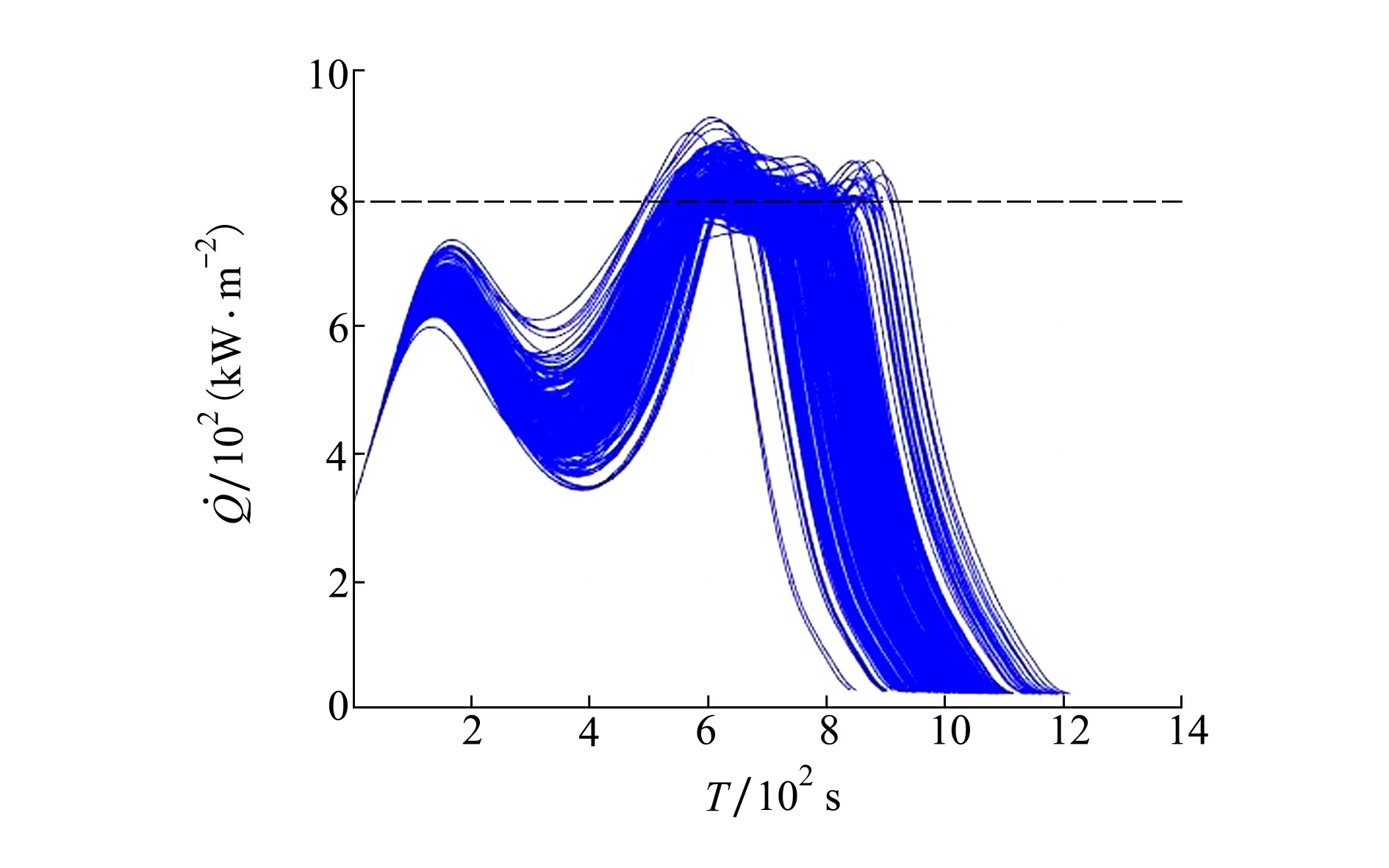
图2 标称情况下优化控制量打靶结果
以下对MC与PC方法的不确定性量化传播性能进行比较。PC方法仿真时,设置一维配点数n=3,多项式的阶数p=2,随机变量维数d=3。
图3~4给出了MC与PC方法的部分状态量均值与标准差的对比曲线。由结果可知,2种方法的均值结果几乎完全一致,而PC方法计算的标准差有一定偏差但在可接受范围内,如经纬度标准差的相对误差仅约3%,即PC方法可替代MC方法进行不确定性量化传播。此外,在计算结果相当的情况下,PC方法只需对动力学方程进行27次积分,而本文的MC方法打靶次数为5 000次,充分体现了PC在计算效率方面的显著优势。
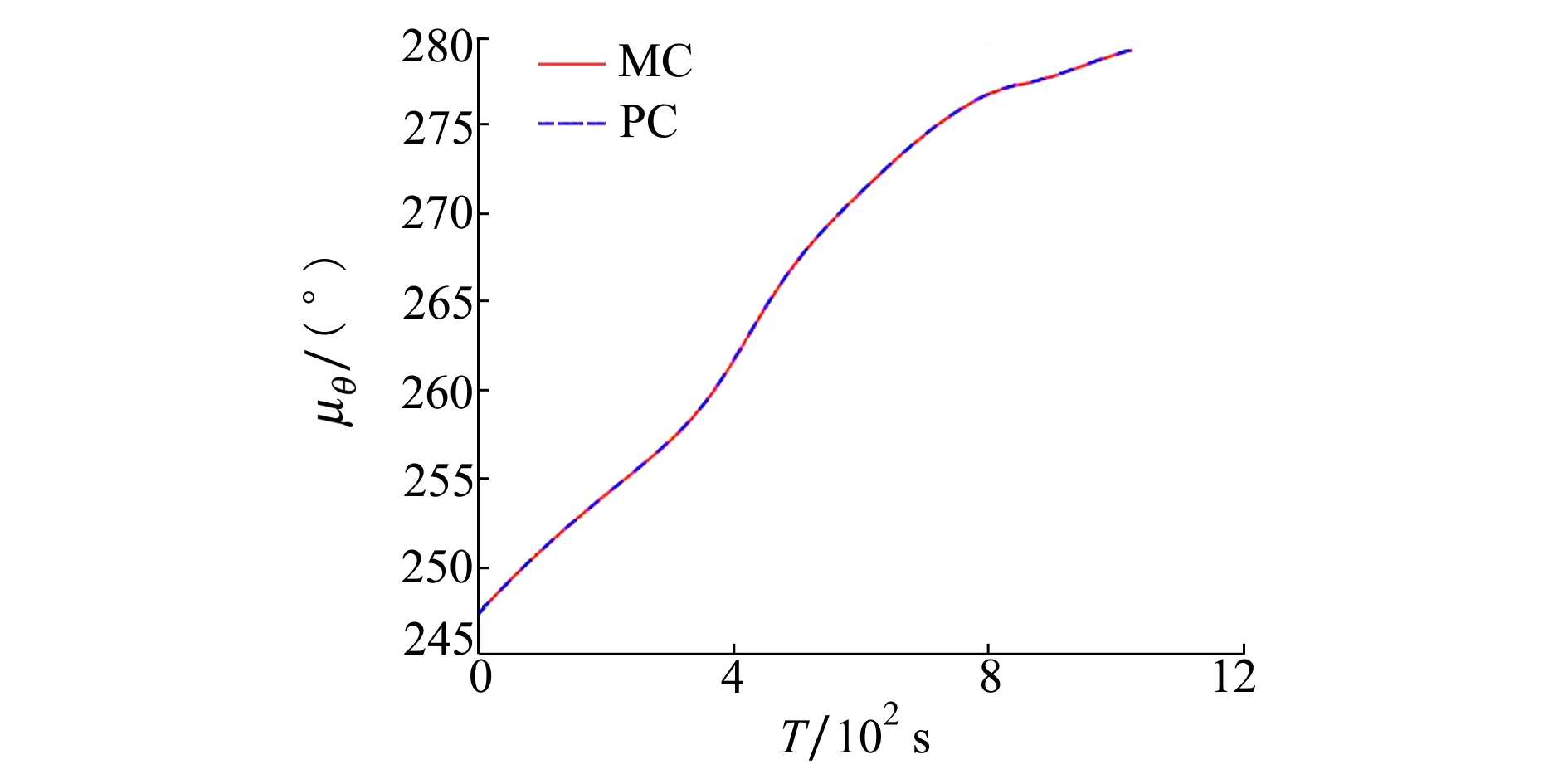
图3 不确定性量化传播的经度均值对比
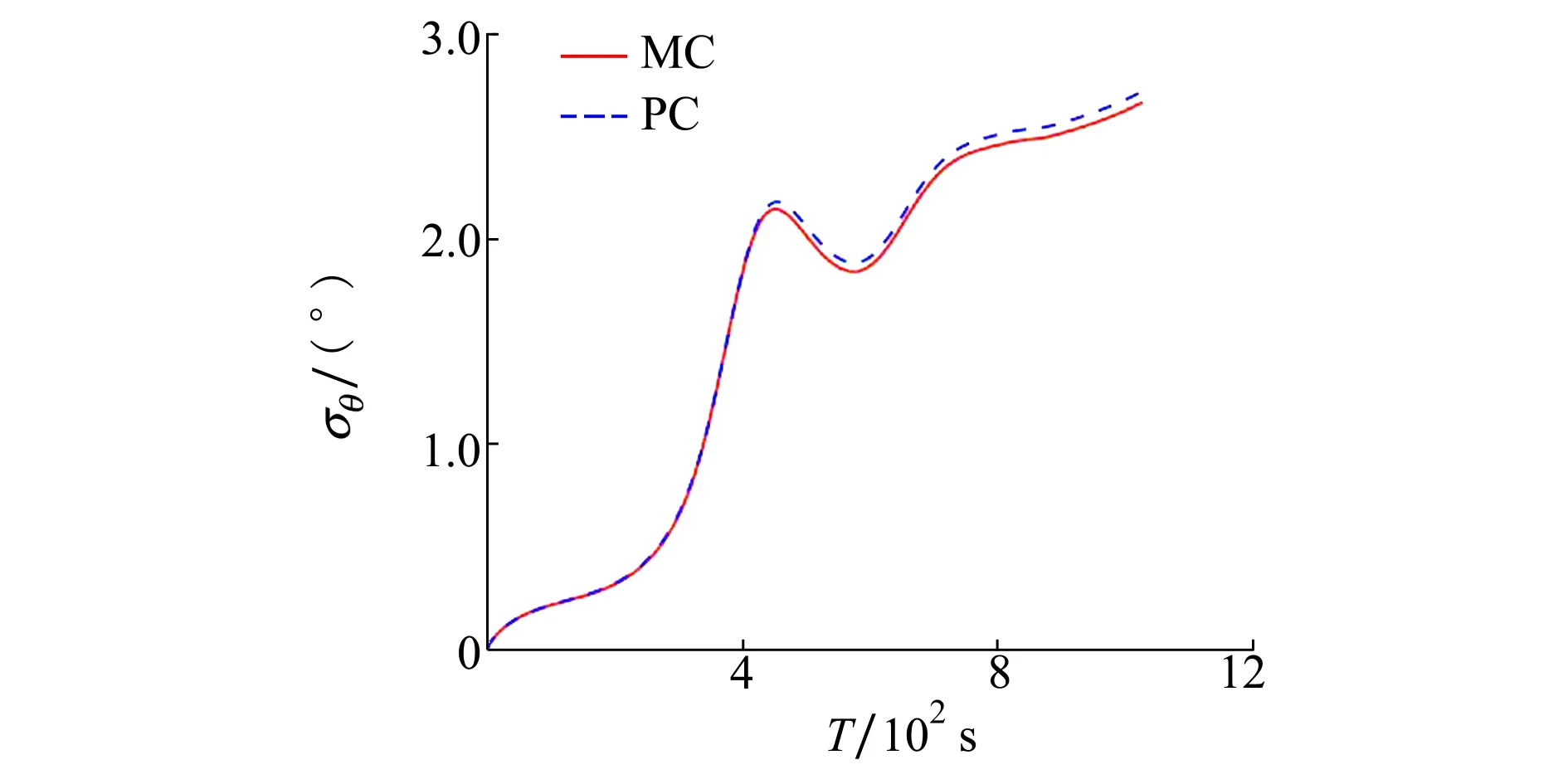
图4 不确定性量化传播的经度标准差对比
4.3 考虑参数不确定的鲁棒轨迹优化仿真分析
为验证所设计算法的可行性,本节开展参数不确定条件下的再入滑翔鲁棒轨迹优化仿真,通过调整权重系数kC,kJ以满足不同的可靠性和鲁棒性需求[13]。采用“DO”、“RO1”与“RO2”分别代表确定性、可靠及鲁棒优化结果,设置RO1参数kC=3,kJ=0;RO2参数kC=3,kJ=1,仿真结果如图5所示。
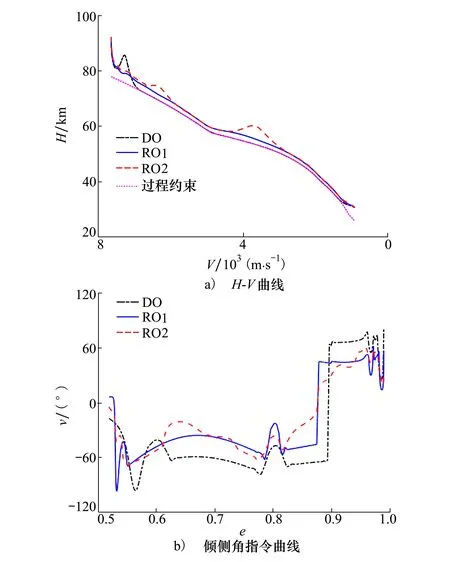
图5 DO、RO1与RO2的优化结果对比
图5对比了3种条件下优化所得H-V与倾侧角指令曲线。由图5a)可知,RO1与RO2对应的高度曲线相较于DO更远离过程约束边界,即优化轨迹的可靠性得到明显提升;与RO1相比,RO2的优化轨迹在中段出现2次拉起,表明这种轨迹形式有利于降低轨迹对不确定因素的敏感度,提升轨迹鲁棒性。由图5b)可知,相较于DO,RO1与RO2初始下降段对应的倾侧角幅值基本维持在0°附近,大小基本一致,表明RO1与RO2对热流峰值的可靠性相当;RO1与RO2继续保持较小的倾侧角幅值以保持更高的飞行高度,提升过程可靠性。
利用图5b)中的倾侧角优化结果进行5 000次蒙特卡罗打靶仿真,以验证鲁棒优化算法的有效性,所得部分参数的统计结果如表2与图6所示。其中,Δμ(·)为均值偏差,Pe为超出过程约束边界的概率,即约束违反率。
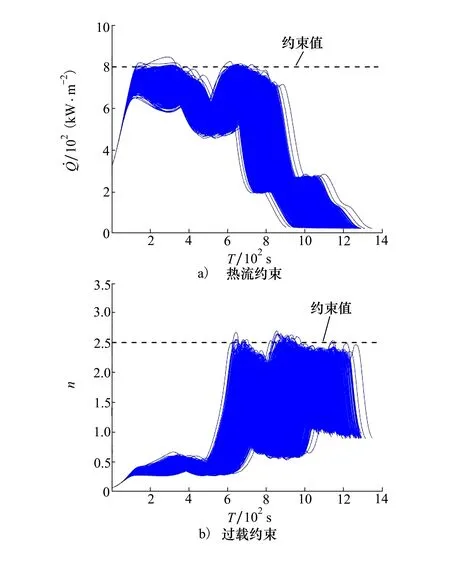
图6 RO2优化控制量打靶结果
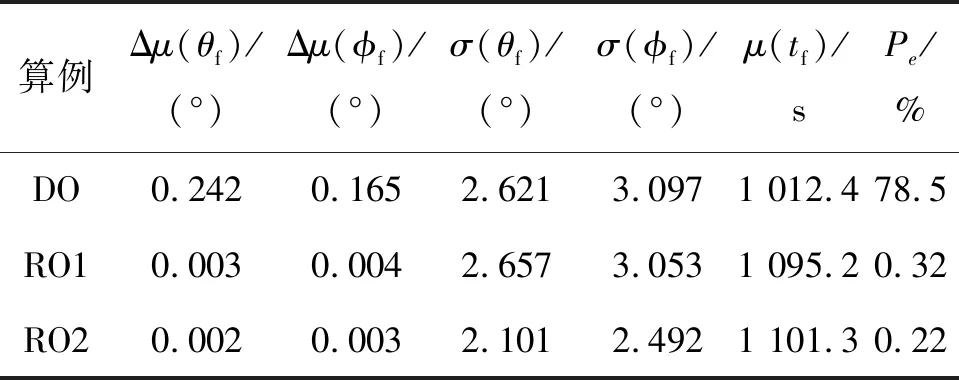
表2 3组仿真打靶数据对比
由表2可知,RO1与RO2的终端经纬度统计精度基本一致,且相较于DO有明显改善,而由于考虑了终端性能的鲁棒性,RO2对应的终端经纬度在三者中最小。由图6a)~6b)及表2可知,相较于DO,RO1与RO2的热流、动压、过载均远离约束边界,约束超出的概率由78.5%分别降低到0.32%与0.56%,可见两者的可靠性均有所提升。与RO1结果相比,RO2在保证轨迹可靠性的同时,对不确定性的敏感度最低,具有更好的鲁棒性。此外,相较于DO结果,RO1与RO2对应的飞行时间均值较大,这是由于不确定性的引入与可靠性约束的施加会造成优化求解的可行域减小,迫使轨迹高度提升导致飞行时间增大;而相较于RO1,RO2的飞行时间均值更大,这是由于RO2的目标函数中综合考虑了飞行时间的均值与终端经纬度方差,而RO1仅考虑了飞行时间均值。可见,轨迹的可靠性与鲁棒性的提升是以牺牲一定的最优性为代价的,需要根据设计需求合理调整权重系数,以权衡轨迹的可靠性、鲁棒性与最优性。
4.4 2种鲁棒轨迹优化算法仿真对比
为验证所设计算法的计算效率优势,将本文算法(convex optimization-polynomial chaos,CO-PC)与现有文献[13]中基于伪谱法与PC的典型鲁棒轨迹优化方法(guess pseudospectral-polynomial chaos,GP-PC)进行对比。设置权重系数kC=kJ=3,其余仿真条件同上,所得优化结果如图7所示。
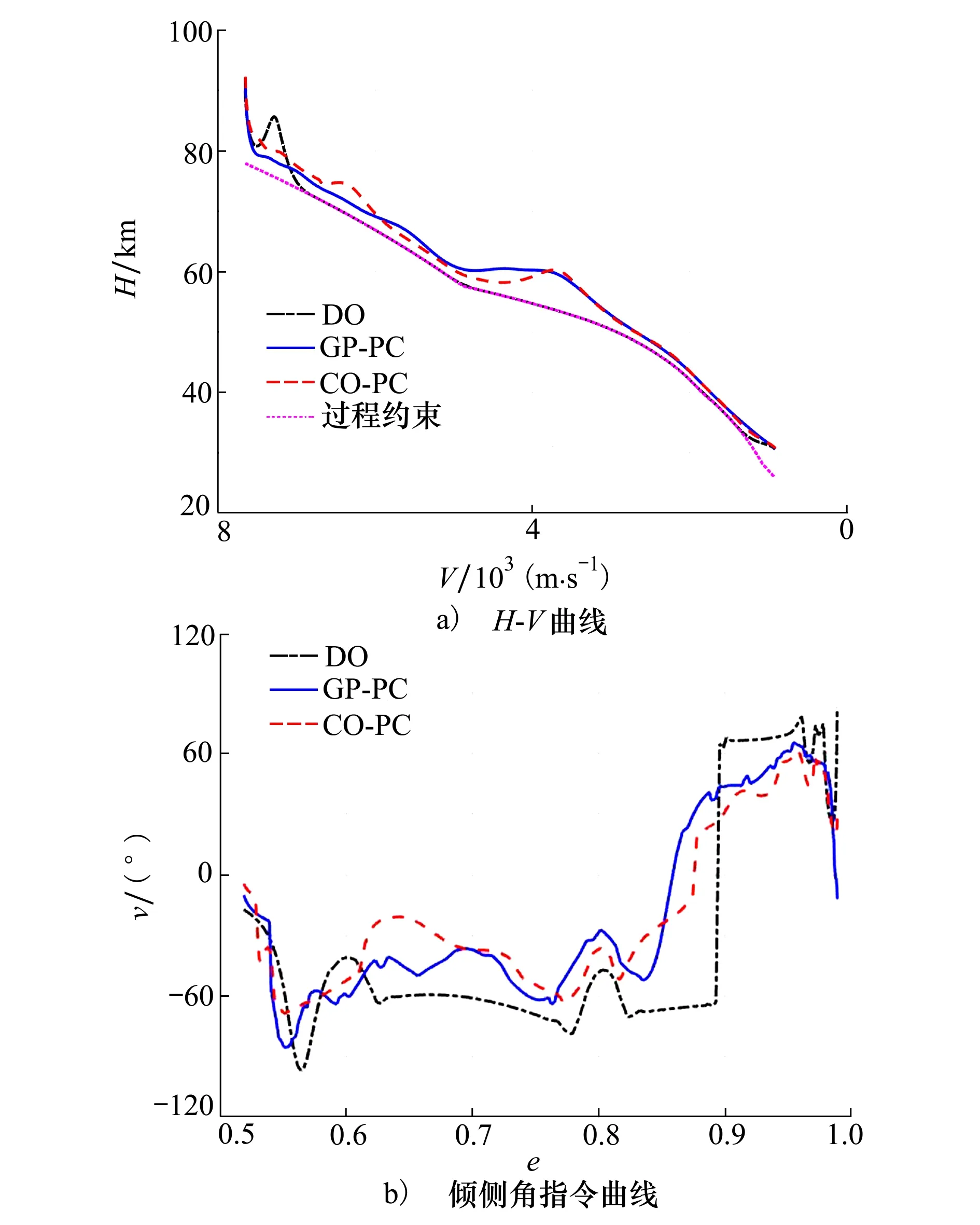
图7 GP-PC与CO-PC的优化结果对比
随后,利用图7b)中的倾侧角优化结果进行5 000次蒙特卡罗打靶仿真,以进一步对比2种鲁棒优化算法的性能,所得部分参数的统计结果如表3所示。其中“DO”为确定性优化结果。
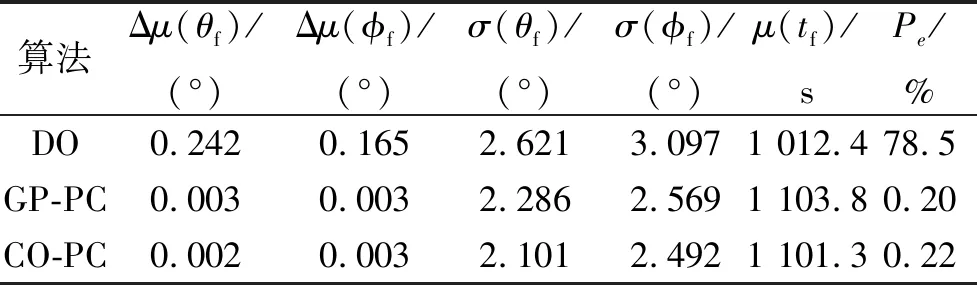
表3 2种方法优化结果的打靶数据对比
由图7a)~7b)可知,2种方法的鲁棒轨迹优化结果基本一致,且对应的高度曲线相较于DO更远离过程约束边界;相较于GP-PC,CO-PC的高度曲线前段更高,且飞行全程存在2次高度拉起过程。由表3可知,两者的约束违反概率及终端经纬度均值精度基本一致,而相较于GP-PC,CO-PC的终端经纬度标准差以及时间均值则更小,表明CO-PC的优化结果鲁棒性更强,目标函数更优。
表4则进一步对比了2种优化算法的计算耗时及待优化变量数。可以看出,CO-PC方法在优化变量数及迭代步数更多的情况下,优化耗时仅为GP-PC方法的10%,表明本文所提出的CO-PC方法能够有效处理状态维数扩展的鲁棒轨迹优化问题,显著提升该问题求解的效率。

表4 GP-PC与CO-PC的数值计算性能对比
5 结 论
针对存在参数不确定的再入滑翔轨迹设计问题,本文研究了一种基于非嵌入式混沌多项式与凸优化相结合的鲁棒轨迹优化算法,理论分析与仿真结果表明:
1) 与确定性轨迹优化和现有典型鲁棒轨迹优化算法相比,本文方法能够显著提升再入滑翔轨迹的鲁棒性与可靠性,降低轨迹对参数不确定性的敏感度,且具有相当的精度和更高的计算效率优势。
2) 轨迹鲁棒性与可靠性的提升以牺牲一定的最优性为代价,通过调整权重系数,能够权衡三者关系,以综合满足轨迹的可靠性、鲁棒性和最优性需求。
3) 所构建的基于高斯求积与非嵌入式混沌多项式的不确定量化传播算法,可实现随机问题的有效转化,且计算精度与MC方法相当情况下,具有显著的计算效率优势。
4) 本文仅考虑了三维随机变量的不确定问题,若进一步增加随机变量维数,会导致扩展状态维数呈指数型增加,难于求解。因此,在高维不确定条件下,如何实现鲁棒轨迹的快速优化求解可作为后续的研究方向。
