太沙基一维渗流固结理论的教学设计与思考
2023-11-21张会领李佩欣
张会领,李佩欣,赖 明
(广东海洋大学海洋工程与能源学院 广东 湛江 524008)
太沙基一维固结理论是研究地基沉降的重要理论基础,也是土力学中的重点和难点。目前在国内教材当中,都是利用高等数学中的偏微分方程、泰勒公式和傅里叶级数等知识得到孔隙水压力的时空分布。这种教学模式逻辑严谨,条理清晰,有丰富的数学内涵,对培养学生的数理分析能力与逻辑思维分析能力有较大的帮助。但是数学公式推导内容繁杂而抽象,对学生的数理能力要求较高,增加了教与学的难度。本文围绕太沙基一维渗流固结理论建立物理模型和数值模型,通过具象化的教学方法重构太沙基一维渗流固结模型的教学设计。
1 饱和土的一维渗流固结理论
饱和土体受压产生固结包括土体中孔隙水排出、土体孔隙体积减小和孔隙水压力转变为有效应力三个过程。
1.1 基本假设
太沙基在分析饱和土体一维渗流固结模型时,进行了如下假设:
①土层均匀且充满水分,没有干燥或局部饱和的情况;②固体颗粒和水分子受力不会发生体积的压缩变化;③变形只发生在土体的垂直方向,侧向变形受到限制;④荷载均匀地施加在土层上,并且只进行一次施载;⑤土体的渗透符合达西定律,并且土体的渗透系数保持恒定;⑥土的压缩系数在固结过程中不发生变化。
1.2 活塞—弹簧—水模型
为了直观解释饱和土体的渗流固结过程,太沙基提出了弹簧—活塞—水的力学模型。光滑正方形筒模拟侧限条件;弹簧模拟土骨架;水体相当于孔隙水;带孔活塞相当于排水顶面,活塞小孔模拟渗透性大小(图1,p74)。

图1 活塞—弹簧—水模型渗流固结过程
如图2 所示(p74),在活塞顶面骤然施加压力的一瞬间,圆筒中的水尚未从活塞的细孔排出时,压力 完全由水承担,弹簧没有变形和受力,即u= ,'=0。经过时间t后,因水压力增大,筒中水不断从活塞底部通过细孔,从活塞顶面流出;从而使活塞下降,迫使受力弹簧压缩。此时,有效应力'逐渐增大,孔隙水压力u逐渐减小,但满足'+u= 。当时间t经历很长后,孔隙水压力u0,管中水停止流出。外力 完全作用在弹簧上。这时有效应力'= ,而孔隙水压力u=0,土体渗流固结完成[1-2]。
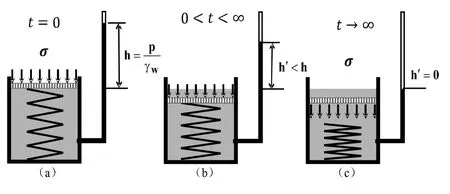
图2 饱和土体的渗流固结过程
2 固结微分方程的建立
2.1 求解思路
在饱和土体一维渗流固结过程中,土体被压缩,土骨架体积发生变化,孔隙体积变小,孔隙水单向流出。在这个过程中,土骨架的压缩受土体压缩性质的影响,其本质是有效应力增加的结果,孔隙水的流出符合达西定律。饱和土体一维渗流固结微分方程建立的思路如图3。
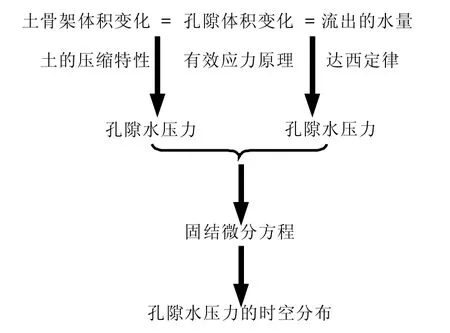
图3 建立一维渗流固结建立微分方程的思路
2.2 求解过程
假设有一个厚度为2H 的饱和粘性土层,上下两个面都为透水面,作用在土体上部的竖直均布荷载无限广阔分布。在任意深度Z 处,取一个微小单元体,设固体体积VS=1(图4)[3]。
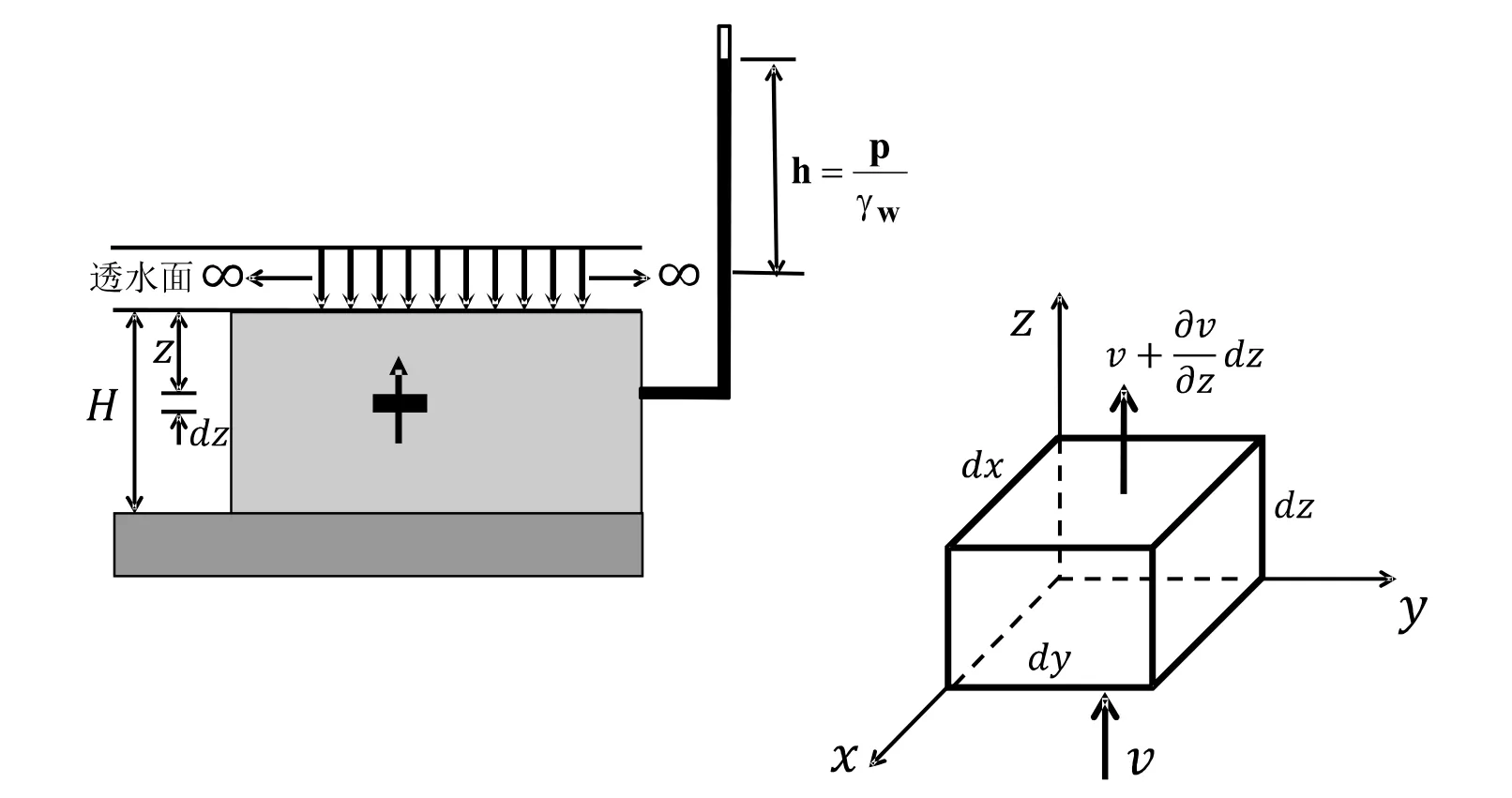
图4 饱和土层的固结
2.3 数值模拟
本文的数值模拟采用Abaqus 软件,对饱和土体进行有限元分析[4]。Abaqus 软件可以满足该理论的六条基本假设及土的渗透系数、孔隙比等物理量。模型建立过程如下:
①创建模型。在软件中建立一个200mm×200mm 的正方形模拟土层,并且赋予该正方形土的性质,设置侧限条件,并在顶部施加一次性的均布荷载;②分析过程。设置孔隙水压力、开始时间和结束时间。③选取不同的时间因子,描绘出曲线图,赋予不同的渗透系数和孔隙比,描绘出曲线图[5]。
该模型参数设置为杨氏模量=10000kN/m,泊松比=0.3,渗透系数=10-7cm/s,孔隙比=1.5,间隙流体比重=10kN/m2(图5)。绘出的曲线图X 轴是渗流路径,Y 轴是孔隙水压力,该曲线图分别表示时间因子等于0.05、0.2、0.7 时,孔隙水压力随渗流路径的变化(图6)。
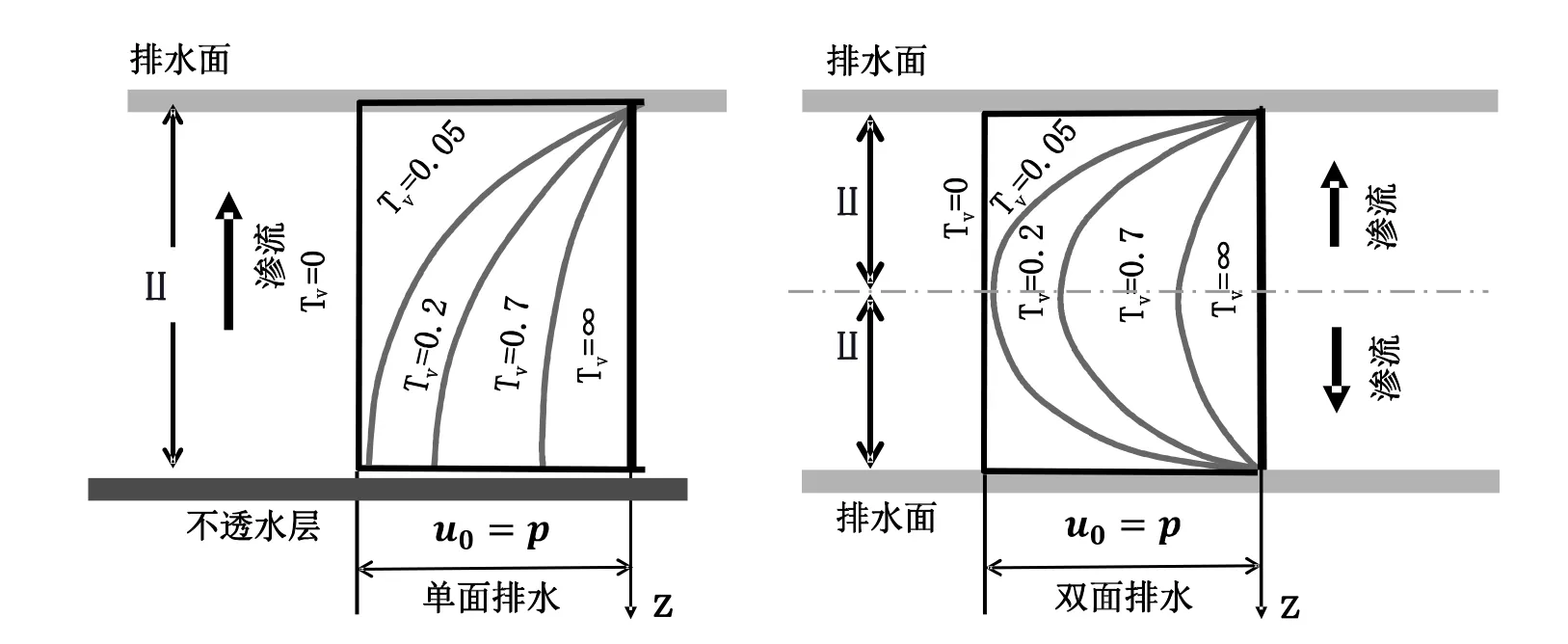
图5 土层在固结过程中孔隙水压力的分布
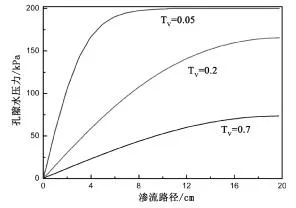
图6 在不同时间因子下,孔隙水压力随渗流路径的变化
在时间因子不变的条件下,孔隙水压力随渗流路径的增大而增大,并且在增大的过程中会趋于平缓;随着时间因子的增大,孔隙水压力的变化减缓;当时间因子趋于无穷时,孔隙水压力变为零,数值模拟结果与数学分析结果一致,符合太沙基一维固结沉降理论。
2.4 教学思考
教师在教学中引入和应用可视化方法,优化了课堂教学内容,可以改善学生的思维习惯,提升学习兴趣。饱和土渗流固结物理模型的建立,使饱和土体渗流固结过程具象化,有助于学生理解渗流固结过程。Abaqus 建立的数学模型清晰地展现了孔隙水压力的时空变化规律,还与数学分析的结果相互印证。
以学生为中心开展教学内容设计是顺利开展教学活动和提高教学质量的前提。在一维固结理论教学内容设计上充分考虑了这一点(图7,p76)。首先,让学生自主预习教材中关于一维固结理论的相关内容,教师上课前先了解学生的自主学习情况,评估学生对单向固结微分方程推导的理解情况。数理基础较好的学生可通过土力学教材进行自学;数理基础较弱的学生可结合土力学教材、弹簧—活塞—水模型、孔隙水压力变化的曲线图、地基沉降量随时间变化的曲线图进行辅助理解。从而激发学生进一步的分析和思考,进而对单向固结理论进行深入理解[6]。
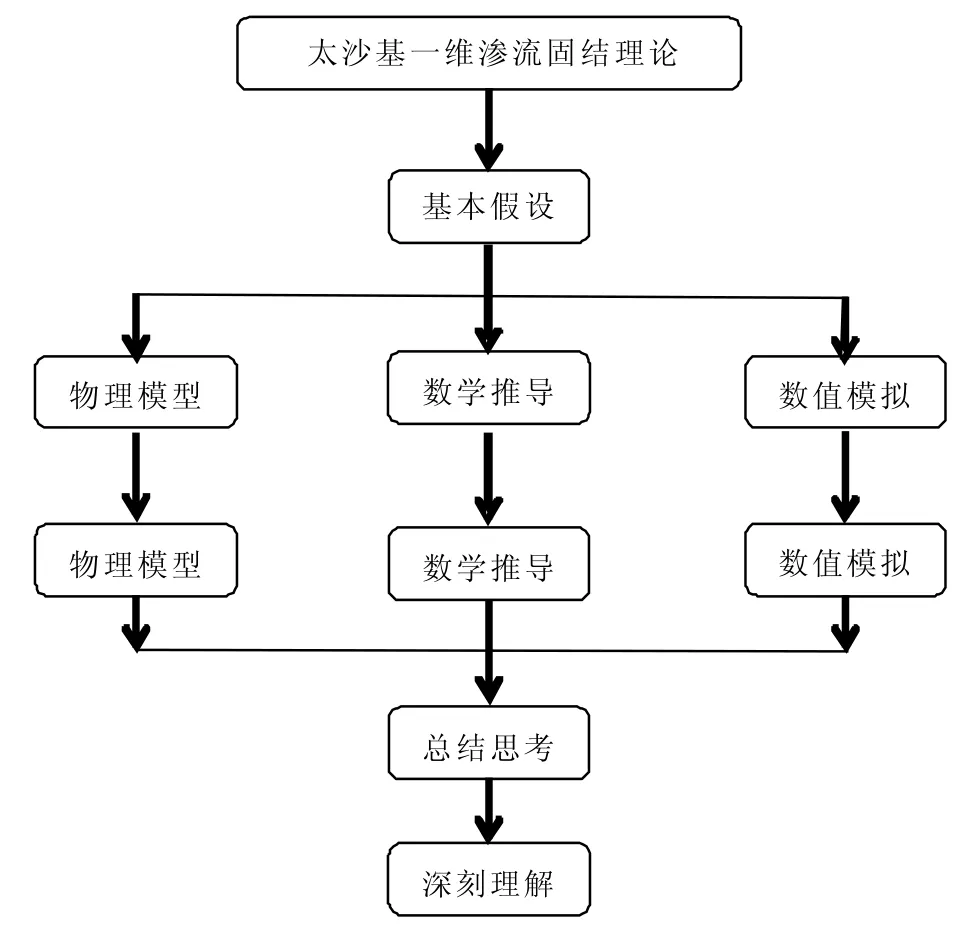
图7 教学优化设计
在传统教学中辅以物理模型以及数学模型可以更好地促使学生直观理解教学内容。物理模型能够突出问题的主要因素,将复杂的问题简易化,将抽象的问题具体化。饱和土渗流固结模型的建立,使饱和土体渗流固结过程具象化,有助于学生理解渗流固结过程,从而将繁杂的数学公式理解得更透彻。学生通过操作物理模型,观察物理现象,在头脑中形成清晰的物理情境,深入理解物理知识的内涵,使物理教学更加具体生动。在教学中引入和应用可视化优化了课堂教学结构,改善了学生的思维习惯,增强了学生的学习兴趣。建立饱和土渗流固结数学模型,描述孔隙水压力与沉降量随时间的变化,使用Abaqus 生成的曲线图能够更加直观地观察到两种关系的变化情况。这不仅可以激发学生对知识点的学习兴趣,而且让学生对知识点的理解更加透彻,不再是对公式演算过程的生搬硬套[7]。
3 结语
太沙基一维渗流固结理论是土力学中理论性很强的内容之一[8]。复杂的公式推导会让学生在学习过程中对所学内容失去兴趣,物理模型与数学模型辅助教学旨在让学生更好地理解该推导过程。教师通过建立数学模型实现教学内容的可视化,将数学公式繁杂的演算过程转化为具体的、形象化的模型,降低了学生理解知识点的难度,一方面便于教师对知识的讲解,另一方面,激发学生的学习兴趣,提高了课堂教学的实效性。
