基于环境承载力的下沉式绿地污染物迁移数学解析模型
2023-11-20吴舒畅杨华展罗昊进朱世俊楼丹阳王和阳
王 亮,吴舒畅,杨华展,罗昊进,朱世俊,楼丹阳,王和阳
(1.浙江大学建筑设计研究院有限公司,浙江杭州 310028;2.中国电建集团华东勘测设计研究院有限公司,浙江杭州 311122;3.温州设计集团有限公司,浙江温州 325000;4.浙江工业大学土木工程学院,浙江杭州 310014)
近年来我国快速城镇化带来的城市不透水下垫面比例逐年升高,降雨径流污染愈发严重,北京市城区雨水径流污染占水体污染负荷12%以上,上海市占20%左右,因而进一步引发了城市水环境污染[1-4]。党中央、国务院高度重视水环境治理问题,《“十四五”全国城市基础设施建设规划》强调,“积极推进海绵城市建设,以水而定,量水而行,构建城市健康水循环,形成与资源环境承载力相匹配的山水城理想空间格局”[5]。
下沉式绿地作为国家海绵城市常见的低影响开发(LID)设施,用于道路源头减排时,主要功能为雨水径流污染控制,且须与自然水土、植被的环境承载力相适应[6-8]。由于初期雨水径流污染性较强,自2022年起,国家强制性规范要求未经净化的初期雨水径流不得进入下沉式绿带[9],但并未给出具体的数据要求。住房和城乡建设部2022年发文强调,“须深刻理解海绵城市建设理念,避免仅从单一专业角度出发考虑问题,应在分析城市生态本底承载力的基础上多专业协同,促进形成生态、安全、可持续的城市水循环系统”[10]。
国外学者于20世纪末、21世纪初对初期雨水径流长期集中入渗对地下水土、植物生长的影响作了深入研究,并根据环境承载力要求对LID设施提出了具体的生态设计要求[11-13]。Nieber等[14]发现雨水回收利用系统中的径流集中入渗会导致地下水中的金属和石油烃超标。Tedoldi等[15]通过对城市可持续排水系统(SUDS)系统土壤进行取样,分析发现SUDS系统具有良好的污染物控制能力,并通过数值模拟方法污染物迁移过程进行模拟,但对设计人员要求较高,须熟练掌握软件使用比需要大量实测数据进行率定。国内对下沉式绿地的研究大多集中于污染物负荷削减效果的试验研究[16-18],而对地下水土、植被环境的影响问题少有研究[19]。李畅等[20]采用室外种植箱的方式进行模拟试验,研究不同植物配置、不同下垫面雨水径流、不同土壤层厚度以及不同污染物浓度对下沉式绿地削减污染物的影响。邓若晨等[21]指出雨水快速下渗过程中是否会对城市地下水造成负面影响值得探讨,并应建立适合工程设计人员使用的海绵城市污染物运移数学模型,用以模拟地下水位溶质运移过程。李海燕等[22]通过文献调研发现,国内目前对结合周边环境生态要求的污染物迁移数学解析模型的建立也仍处于起步阶段,这些都制约了下沉式绿地的合理应用。因此,建立一种简洁有效的数学解析模型来揭示雨水径流污染物在下沉式绿地的迁移规律,同时评价其对周边生态环境的影响势在必行。
基于上述研究基础,本文拟建立基于环境承载力的污染物迁移数学解析模型,技术路线如图1所示。通过耦合雨水径流下渗数学模型和污染物在地下水土迁移数学模型[23-24],系统性建立了下沉式绿地雨水径流污染物一维迁移数学解析模型。通过模型计算揭示雨水径流污染物在下沉式绿地内的迁移规律,并给出相对浓度变化及污染物累计通量去除率的解析表达式。同时,根据所处环境承载力要求提出生态设计约束条件,有利于海绵城市设计,也更有利于加强城市自然生境保护,提高自然生态系统活力,构建连续完整的城市生态基础设施体系。
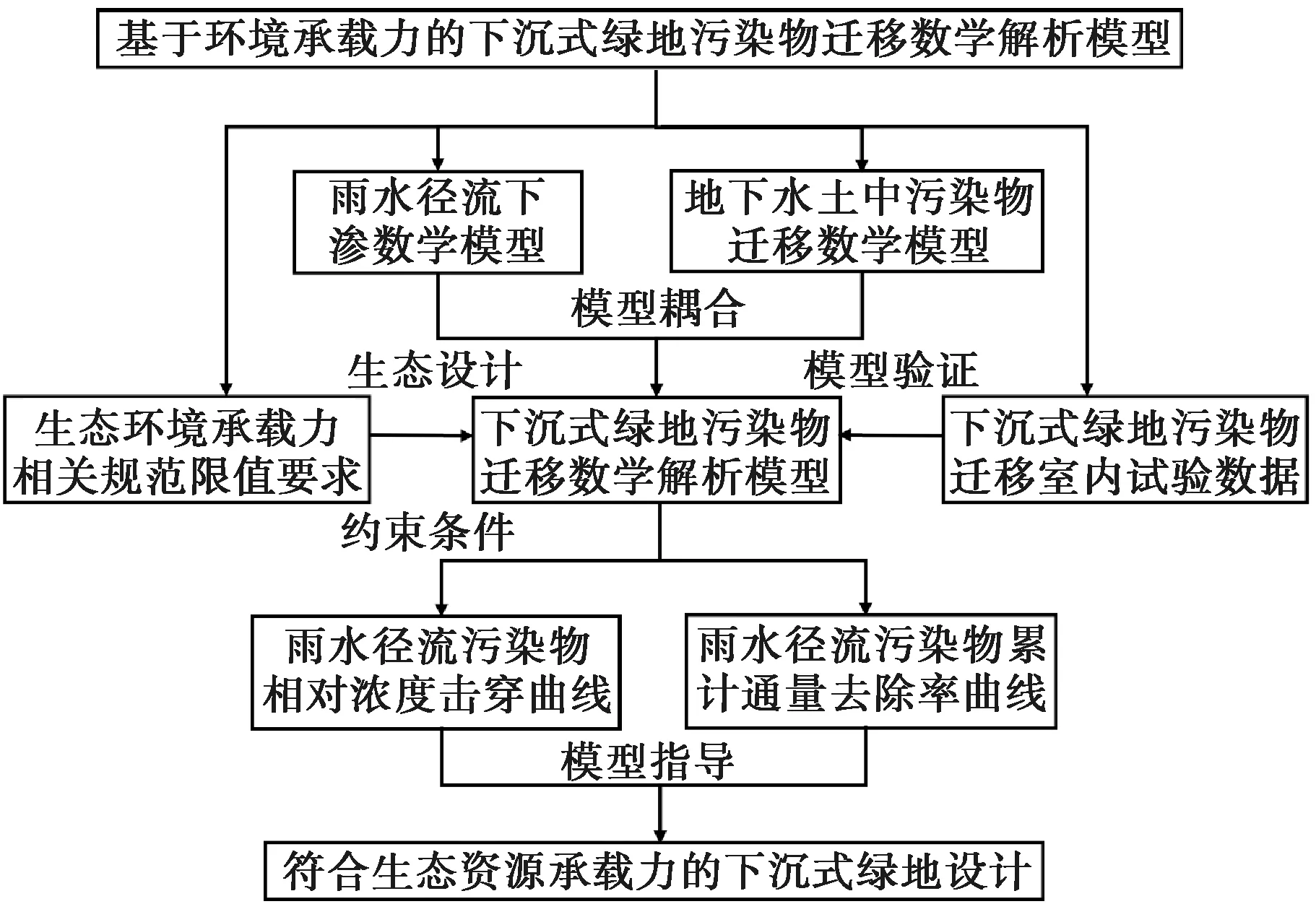
图1 技术路线
1 基本假设与数学模型
1.1 基本假设
如图2所示,在建立下沉式绿地雨水径流污染物迁移数学解析模型时,主要基于以下假设:(1)考虑雨水径流污染物在下沉式绿地均匀下渗,并服从达西定律;(2)下沉式绿地土层一般为2层,种植土层及中粗砂层,两土层之间考虑污染物浓度连续与通量连续;(3)污染物在地下水土中主要迁移方式为对流、扩散以及吸附作用;(4)污染物在土中的扩散与对流是一维的;(5)下边界考虑半无穷。
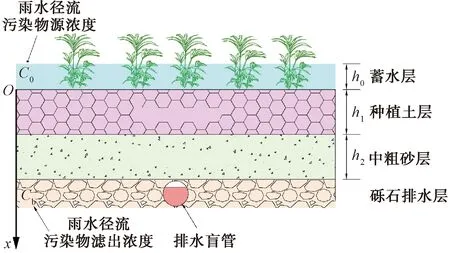
图2 下沉式绿地雨水污染物迁移[25-26]
1.2 控制方程
目前应用较多的雨水下渗数学模型是基于达西定律所推导的,其表达式如式(1)。
(1)
其中:va——达西流速,m/s;
Q——雨水下渗量,m3/s;
A——下沉式绿地的面积,m2;
ke——下沉式绿地各土层的垂直等效渗透系数,m/s;
h0——蓄水层水位高度,m;
h1、h2——下沉式绿地种植土层、中粗砂层的厚度,m。
(2)
其中:k1、k2——种植土层、中粗砂层的渗透系数,m/s。
基于上述假设,雨水径流污染物在下沉式绿地中的运移方程可描述如式(3)~式(4)[27]。
(3)
(4)
其中:C1、C2——种植土层、中粗砂层的污染物质量浓度,mg/L;
D1、D2——种植土层、中粗砂层的扩散系数,m2/s;
v1、v2——种植土层、中粗砂层的渗流速度,m/s;
R1、R2——种植土层、中粗砂层的阻滞因子;
t——时间,s;
x——空间坐标,m。
式(3)、式(4)的初始条件如式(5)~式(6)。
C1(x,0)=0
(5)
C2(x,0)=0
(6)
相应的边界条件如式(7)~式(10)。
C1(0+,t)=C0
(7)
(8)
(9)
C2(∞,t)=0
(10)
其中:n1、n2——种植土层、中粗砂层的孔隙率;
C0——雨水径流污染物源质量浓度,mg/L。
1.3 数学模型的解
对流扩散方程在单层土质衬垫的情况下,Ogata等[28]给出了其相对浓度的经典解析解。而本文数学解析模型中涉及两层土质衬垫,两层土质衬垫的底部解析解较为复杂,难以获得。因此,通过结合前期研究成果所提出的污染物运移参数等效模型[23],可得到下沉式绿地的等效底部解析解,相对浓度(CN)表达式如式(11)~式(15)。
(11)
(12)
(13)
(14)
(15)
其中:Cb——下沉式绿地底部砾石排水层污染物击穿质量浓度,mg/L;
erfc——互补误差函数;
TR——时间因子;
PL——Pelect数;
ve、De——种植土层、中粗砂层的等效渗流速度和等效扩散系数;
tb——指示性污染物击穿时间,s。
污染物瞬时通量FI可由式(16)~式(19)求得[29]。
(16)
(17)
(18)
(19)
从而可以得到污染物累计通量FA如式(20)~式(21)。
(20)
(21)
则污染物累计通量去除率RO如式(22)。
(22)
2 模型验证
高天赐[30]通过人工配水模拟道路径流,以土柱试验为手段,研究了下沉式绿地人工滤层对雨水中Pb2+的截留规律。该试验采用有机玻璃柱,内部内径为5 cm,长度为60 cm,自上而下依次为蓄水层、种植土层、中粗砂层、砾石排水层。模拟试验期间保持上部淹水深度为5 cm,模拟径流设计质量浓度恒定为100mg/L,模拟径流自上而下通过试验土柱,收集并记录砾石排水层的液体污染物浓度。通过调研文献[23,27,31-32]及该试验实测数据[30],具体模拟参数如表1所示。

表1 试验土层参数取值
如图3所示,本文解析模型与试验数据拟合较好,决定系数R2=0.994 1,证实了本文下沉式绿地雨水污染物迁移数学解析模型的合理性与有效性,同时体现了在实际工程中拟合的实用性。

图3 解析模型与下沉式绿地雨水污染物Pb2+试验数据对比
3 工程应用
全文强制性规范《园林绿化工程项目规范》(GB 55014—2021)[9]中规定,未经净化处理的车行道初期径流雨水不得直接排入道路绿带。因初期雨水冲刷过车行道路面,水质较差,含有大量污染物,不利于植物生长,同时也对地下水土造成不同程度的污染。
Pb元素不是植物生长的必须元素和有益养分,浓度超过植物耐受程度对产生毒害作用,高浓度的Pb亦会严重阻碍植物的生理活动[33]。因此,以重金属Pb2+为例,其运移参数同表1,通过本文数学解析模型计算以探究下沉式绿地不同蓄水高度、中粗砂层不同的渗透系数对污染物迁移的影响,以及未经净化雨水径流对植物和地下水土造成的污染程度。
3.1 不同蓄水高度对污染物迁移的影响
根据目前海绵城市建设情况,一般下沉式绿地蓄水高度常为5~15 cm。据学者[34-35]统计,国内普通道路雨水径流Pb2+质量浓度为0.05~0.07mg/L。而根据《地下水质量标准》(GB/T 14848—2017)的规定,Pb2+质量浓度≤0.005mg/L(地下水Ⅱ类标准),取雨水径流Pb2+质量浓度为0.05mg/L,则CN限值为0.1。考虑到城市内短历时降雨一般为120~180 min,长历时降雨一般为24~72 h,下沉式绿地排空时间宜为24~48 h[8,36],如图4所示,下沉式绿地相对浓度击穿时间随蓄水高度的增加而减少。对于城市短历时降雨(120~180 min)而言,下沉式绿地能较好实现径流污染控制的功能,同时满足《地下水质量标准》标准。但对于长历时(24~72 h)降雨而言,蓄水高度h0=5 cm时,相对浓度击穿时间约为110 h,蓄水高度h0=10 cm时,相对浓度击穿时间约为54 h,这对于较为极端的72 h长历时降雨而言,雨水径流污染物已有可能对植物及地下水土造成污染。对于蓄水高度h0=15 cm时,相对浓度击穿时间约为36 h,较蓄水高度h0=5 cm时约缩短了67%,在60 h时已污染物Pb2+浓度已完全击穿,在长历时降雨情况下,会对植被及地下水土造成污染。

图4 不同蓄水高度Pb2+相对浓度击穿曲线
此外,从污染物累计通量去除率角度分析,如图5所示,对于短历时降雨,不同的蓄水高度的污染物累计通量去除率较高,均能满足设计要求。对于长历时降雨,蓄水高度h0=5 cm的污染物累计通量去除率接近100%,能较好实现源头减排阶段雨水径流污染控制的目标要求。对于长达72 h的长历时降雨,蓄水高度h0=10 cm的污染物累计通量去除率约为90%;蓄水高度h0=15 cm的污染物累计通量去除率约为65%。因此,蓄水高度的增加会导致下沉式绿地污染物累计通量去除率下降,蓄水高度分别从5 cm增大至10 cm和15 cm,依次使污染物累计通量去除率减少了10%及35%。

图5 不同蓄水高度Pb2+污染物累计通量去除率
结合园林规范对植物生长保护的要求[9],根据数学解析模型计算结果,建议初期雨水径流须经净化后排入下沉式绿地,同时应满足生态设计约束条件[式(23)],即应通过数学模型计算保证在最不利降雨历时(或下沉式绿地最大排空时间,两者取大值)的砾石排水层污染物浓度应不大于相关国家规范要求的限值。
(23)
其中:Cs——相关规范要求的限值,mg/L;
tp——下沉式绿地最大排空时间,s;
tr——最不利降雨历时,s。
3.2 土壤不同渗透系数对污染物迁移的影响
鉴于中粗砂具有较好承载力、透水性好,而且可就地取材,施工方便,同时为保证调蓄能力,换土层常采用中粗砂,应用于海绵城市的中粗砂渗透系数常为2.0×10-4~5.0×10-6m/s[37-38]。
图6揭示了蓄水高度为5 cm时,中粗砂层渗透系数越小,相对浓度击穿时间越长。当中砂层渗透系数k2=5×10-6m/s时,击穿时间为160 h,而渗透系数为2×10-5m/s和2×10-4m/s的相对浓度击穿时间依次是104 h和84 h,均满足长历时降雨情况下对植物及地下水土的生态设计要求。
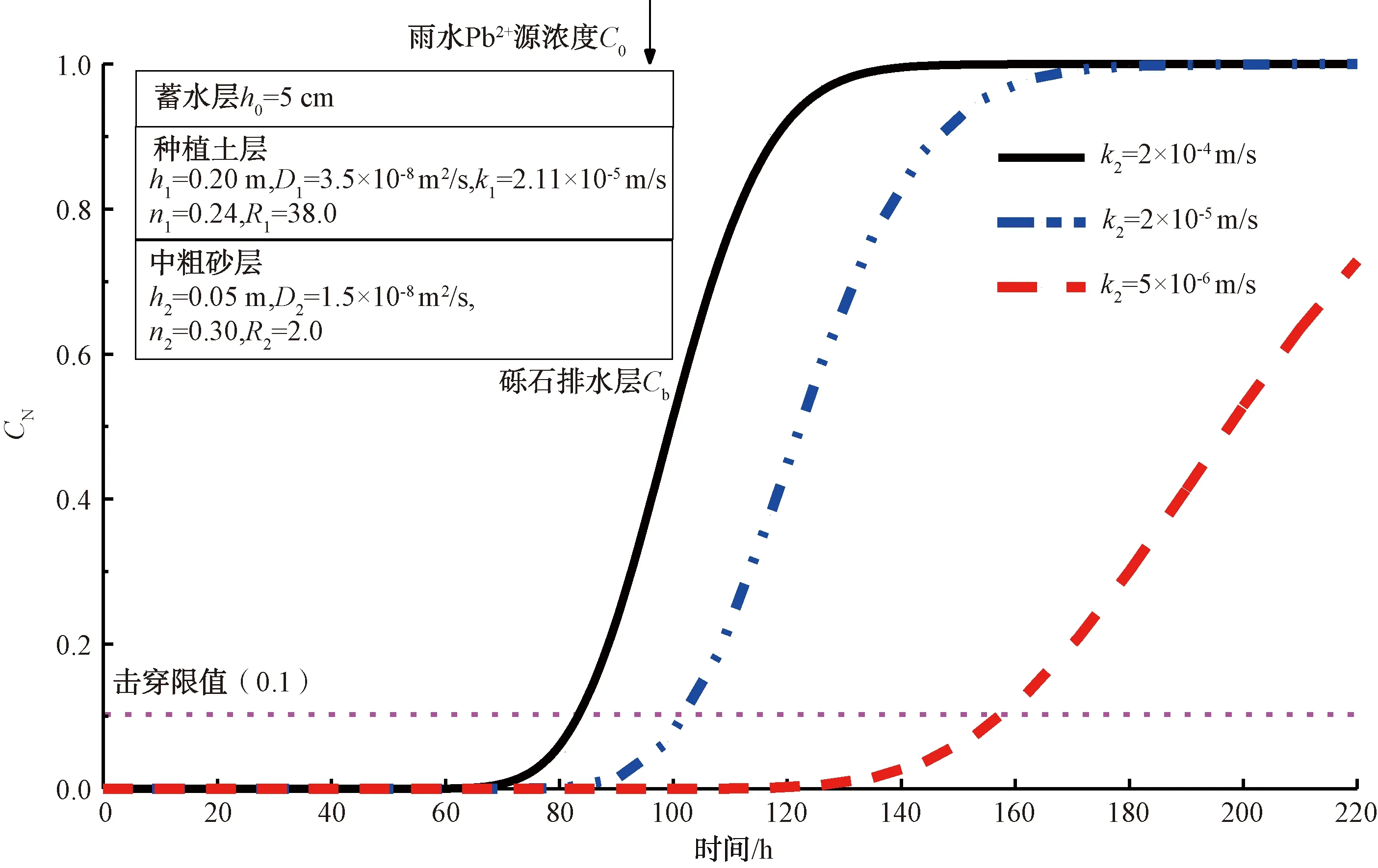
图6 中粗砂层不同渗透系数的Pb2+相对浓度击穿曲线
如图7所示,当蓄水高度为10 cm时,以72 h为例,渗透系数k2=2×10-4、2×10-5m/s和5×10-6m/s的污染物累计通量去除率依次为70%、87%和99%。因此,随着中粗砂层渗透系数的减小,污染物累计通量去除率也随之增大。
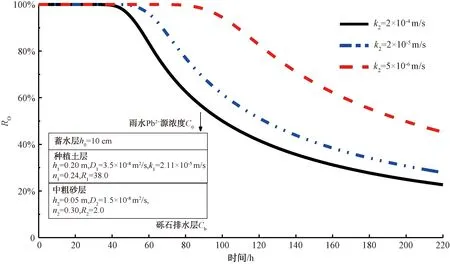
图7 中粗砂层不同渗透系数的Pb2+污染物累计通量去除率
此外,根据前文分析,若设计不满足生态设计约束条件式(23)要求,可通过以下两种工程措施优化下沉式绿地设计:1)减少下沉式绿地蓄水空间高度,具体设计时可选取各地海绵城市设计导则或图集的下限,同时也减少淹水高度,利于植物种类选取及生长,使下沉式绿地更具有景观美感;2)减小中粗砂层的渗透系数,以延长污染物浓度击穿时间,增大污染物累计通量去除率,一般可通过换填,而当换填土渗透系数仍不满足生态设计约束条件时,可在下沉式绿地下敷设一层不透水材料,如钠基膨润土防水毯(GCL),以达到整体减少渗透系数的要求。
4 本研究模型局限及拓展研究方向
考虑到降雨历时中微生物降解的有限性,同时避免方程解过于复杂冗长,本研究模型主要考虑污染物在地下水土中对流、扩散以及吸附作用,而并未考虑地下水土中微生物降解作用。因此,对于易被微生物短时间降解的污染物,模型计算结果可能偏于保守。进一步推导包含生物降解作用的下沉式绿地雨水径流污染物迁移数学模型可作为下一步研究方向,以期更完整地揭示迁移机理,以利生态环境评估以及海绵城市设计优化。
5 结论
基于经典的对流扩散方程,本研究系统构建了下沉式绿地雨水径流污染物迁移的一维数学解析模型,并给出污染物相对浓度变化与污染物累计通量去除率的数学解析表达式。采用下沉式绿地污染物迁移的室内试验数据验证了本文数学模型的合理性与可靠性。
通过应用该数学解析模型,分别得到了下沉式绿地Pb2+污染物击穿曲线以及污染物累计通量去除率曲线。并发现在设定条件下,下沉式绿地蓄水高度从5 cm增长至15 cm,会使其污染物累计通量去除率减少35%,污染物浓度击穿时间缩短67%。模型还揭示了污染物击穿时间和累计通量去除率随下沉式绿地土层渗透系数减小而增大的规律。基于本文模型,给出了生态设计约束条件,避免下沉式绿地的设置对植被及地下水土造成污染。
本文所提出的数学解析模型可为海绵城市设计、城市水环境治理、黑臭水体治理、地下水土污染控制等工程提供理论依据和应用方案,尤其是在《“十四五”全国城市基础设施建设规划》印发后,蓝绿交织、灰绿融合、连续完整的城市生态基础设施系统建设越来越受到重视的今天有广阔的应用前景。