最优插值法在堆芯三维功率分布重构中的应用

王洋洋*，孙晓晖，石兴伟

（1.电力规划设计总院，北京；2.中国核电工程有限公司，北京；3.生态环境部核与辐射安全中心，北京）

概述

最优插值法属于数值同化理论的一种，可将测量数据和数值模型的模拟结果进行融合，生成具有空间一致性、时间一致性和物理一致性的数据集，改善模型模拟精度[1]。最优插值法可将程序功率分布计算值和探测器功率分布测量值进行融合，对生成更加准确的堆芯三维功率分布具有重要意义。

本文采用CASMO4E/SIMULATE3 程序建立60 万千万级压水堆核电厂堆芯三维功率分布计算模型，计算堆芯三维功率分布。采用最优插值法将堆芯三维功率分布计算值和堆芯三维功率分布探测值进行融合，重构堆芯三维功率分布并对重构结果进行评估。

1 模型建立

1.1 程序介绍

CASMO4E 程序主要功能是产生计算工况下的两群均匀化常数。CMSLINK 程序主要功能是将CASMO4E 程序产生的数据转换为可被SIMULATE3 使用的二进制数据库。SIMULATE3 程序主要功能是计算堆芯在各燃耗状态下的堆芯功率分布等。

1.2 模型建立

某60 万千瓦级压水堆核电厂堆芯热功率为1 930 MW。堆芯有121 个燃料组件，首循环包含1.9%、2.6%和3.1%三种富集度的燃料，堆芯有33 束控制棒组，包括25 束调节棒组和8 束停堆棒组。首循环堆芯装载见图1。

图1 首循环堆芯装载

1.3 功率计算

将反应堆堆芯轴向划分为16 个节块，径向一个组件一个节块。设定最底层为第1 层，最顶层为第16层。计算工况是堆芯燃耗5GWD/TU、100%满功率运行、棒全提、平衡氙。采用SIMULATE3 程序计算堆芯16 层的共计1936 个节块的归一化功率分布。计算显示，第1 层计算值和参考值最大相对偏差为5.77%，第8 层为2.86%，第13 层为1.63%。堆芯底端和顶端功率分布相对偏差比堆芯中部的偏大，主要是因为堆芯底端与顶端节块的绝对功率值比较低，导致相对偏差的增大。

2 最优插值法原理

最优插值法可以将系统在某一状态下的背景场与相关的测量数据相结合，来估计系统在某一状态下的真值场[2-3]。基本原理是：节块上的分析值由节块上的背景值加上修正值而得到，修正值由观测值与背景值的偏差加权求得，权重系数的选取使分析值的误差最小。权重矩阵是通过观测空间的背景误差协方差矩阵乘以总的误差协方差矩阵的逆来求得，其中总的误差协方差矩阵是处理之后的背景误差协方差与观测误差协方差的和。最优插值法基本方程为[4]：

式中：xa为分析场；xb为背景场；yo为观测场；W 为权重矩阵；H 为观测算子；B 为背景场误差协方差矩阵；R为观测场误差协方差矩阵。

通过构建观测算子H 连接背景场与观测场，可将背景场变换为与观测场一致的维数以实施运算。

背景场误差协方差矩阵B 是最优插值法里最关键的矩阵，包含所有背景场误差的方差还有各个背景误差之间的协相关[5]。背景场误差协方差矩阵定义为：

观测场误差协方差矩阵R 定义为：

因为背景场误差协方差矩阵B 和观测场误差协方差矩阵R 计算公式(3)和(4)中包含真值场xt，而真值场无从获取。因此需要通过协方差的性质借助简化假设来近似确定矩阵B 和R。

背景场误差协方差矩阵为一对角阵，可借助背景误差方差矩阵D 和背景误差相关矩阵C 将B 标准化[6]，如公式(5)所示：

其中背景误差方差矩阵D 表达为：

式中：对角元素值为方差的均值。

背景误差相关矩阵C 表达为：

矩阵C 可采用三维情形二阶自回归模型来构造[7]：

式中：Lr是水平方向的特征尺度；Lz是垂直方向的特征尺度；r 是节块间水平距离，|z|是节块间垂直距离。

观测场误差协方差矩阵R 也是一对角阵，假定两次观测间的误差不相关，即：

则矩阵R 非对角元素值均为零，矩阵R 对角元素可由下式近似确定：

式中：α是一个与仪器测量精度有关的常数，α取值在0 和1 之间，α越趋向于零，表示仪器测量精度越高[8]。观测场误差协方差矩阵可通过下式表示：

3 堆芯三维功率分布重构

采用最优插值法重构堆芯三维功率分布时，堆芯总共划分为1 936 个节块，其中608 个节块可被堆内探测器探测。依据最优插值法建立矩阵，其中背景场向量xb是1 936×1 维；观测场向量yo是608×1 维；观测算子H 是608×1 936 维；背景场误差协方差矩阵是1 936×1 936 维；观测场误差协方差矩阵R 是608×608 维；权重矩阵W 是1 936×608 维。

通过最优插值法基本方程，得到1 936×1 维的分析场向量xa。将分析场向量xa归一化处理，得到堆芯三维归一化功率分布。其中第1 层、第8 层和第13层的功率分布重构值见图2～图4。

图2 第1 层堆芯功率分布重构值

图3 第8 层堆芯功率分布重构值

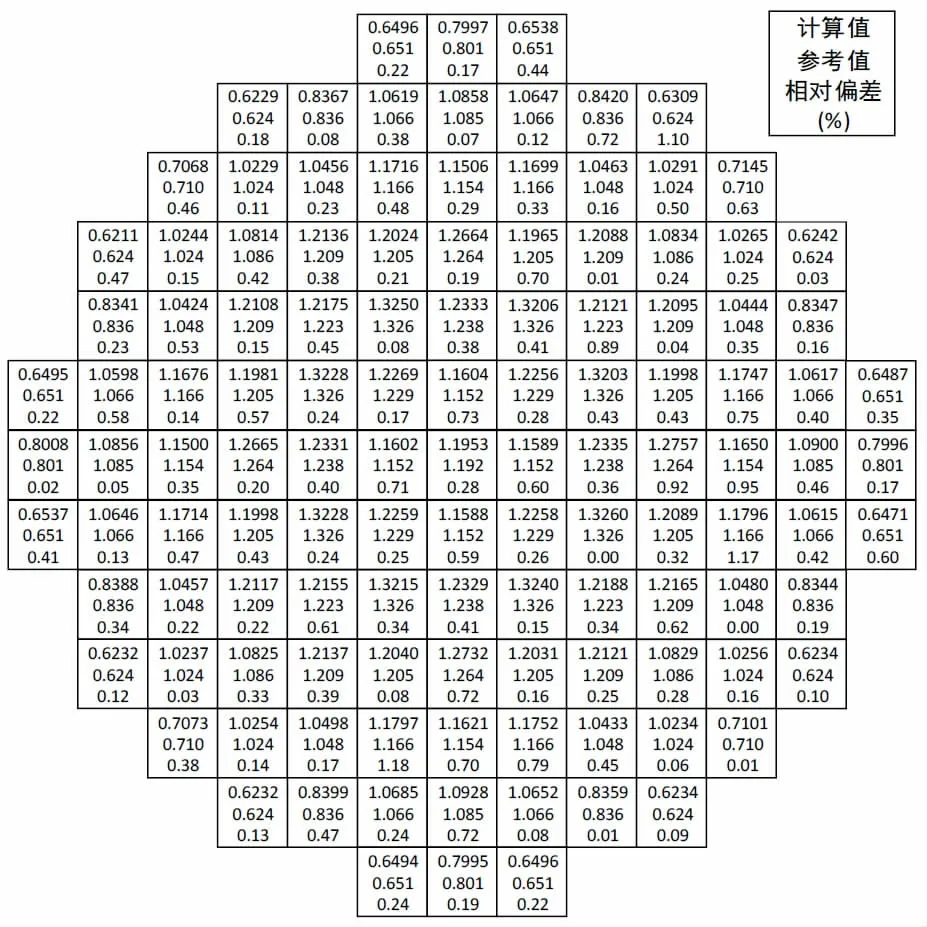
图4 第13 层堆芯功率分布重构值

表1 为堆芯三维功率分布第1 层、第8 层和第13层的计算值、重构值与参考值间平均相对偏差。可见利用最优插值法重构堆芯三维功率分布，功率分布重构值比程序计算值更加接近实际参考的功率分布。

表1 第1、8、13 层平均相对偏差

定义背景值与观测值的偏差的绝对值为|Δ1|，分析值与观测值偏差的绝对值为|Δ2|，同化效果定义为下式：

易见，若E=0，则同化起到了决定性作用，分析值与观测值完全一致；若0＜E＜1，则同化起到了部分作用，且当E 值越小，则同化效果越好；若E=1，则同化没有起到作用，分析值和背景值完全一致；若E＞1，则同化起到了反作用，分析值比背景值更加偏离观测值。

表2 为堆芯三维功率分布16 层每层的同化效果。每层的同化效果均在0 和1 之间，说明采用最优插值法进行堆芯功率重构起到了正向作用。16 层的平均同化效果为0.189 0，同化效果较好。

表2 堆芯三维功率分布同化效果

4 结论

以60 万千瓦级压水堆核电厂堆芯为研究对象，采用最优插值法重构堆芯三维功率分布。每层功率分布同化效果均在0 和1 之间，数据同化起到正向作用，堆芯三维功率分布重构值比程序计算值更接近实际功率分布。