基于美国抽烟数据的时空自回归模型的统计推断
2023-11-18吴越怡黄振生
吴越怡 黄振生


收稿日期: 2023-04-23
作者简介:吴越怡(1999—),女,安徽六安市人,硕士研究生,主要从事非参数统计研究;通讯作者:黄振生(1976—),男,安徽濉溪县人,教授,博士生导师,主要从事非参数统计研究.
引用格式:吴越怡,黄振生.基于美国抽烟数据的时空自回归模型的统计推断[J].安徽师范大学学报(自然科学版),2023,46(5):418-424.
DOI:10.14182/J.cnki.1001-2443.2023.05.002
摘要:针对目前文献中大多数时空模型的建立大都需要提前指定相关的空间权重矩阵 ,而当空间权重矩阵形式设定错误时,模型的解释性变得极为不可靠,预测能力也大大降低的问题,提出了更为一般的时空自回归模型来拟合美国抽烟需求数据并进行单步与多步预测,模型将空间权重矩阵转化为带估的时空系数矩阵,采用基于Yule-Walker方程的广义矩估计法和基于Yule-Walker方程的最小二乘两种方法来估计系数矩阵,最终的两种预测方法结果均表明建模效果较好。另外模型分析结果也表明:人均吸烟包数与人均可支配收入呈正相关关系,而人均吸烟包数与每包香烟的零售价格呈负相关关系,均与现实意义相符。
关键词:时空数据;时空自回归 ;Yule-Walker方程;广义矩估计;香烟需求
中图分类号:O212.1;F293.33 文献标志码:A 文章编号: 1001-2443(2023)05-0418-07
引言
近来随着时空数据变得越来越丰富,时空建模在研究中受到越来越多的关注。时空观测数据的广泛可用性刺激了各学科的研究,如经济学、环境科学、流行病学等。但与此同时,时空数据的生成规模和复杂程度远远超出了此前的想象。例如,有许多大规模的经济研究是基于在人口普查区、城市或县一级收集的面板数据进行的,这些数据具有隐含且复杂的空间结构。数据中的观测值可以在空间或时间上定期或不定期分布。复杂的数据就需要足够灵活的统计模型来适应潜在的规律,所以尽管近年来时空模型越来越流行,但增强时空建模和分析能力仍然是一个长期的挑战。首先含有空间元素的模型可以被分为三类,分别为非面板空间(SD)模型、静态面板空间(SPD)模型、空间动态面板(SDPD)模型。SD模型主要处理截面空间数据的空间交互效应和空间异方差。Cliff等人(1973)[1]、Kelejian和Prucha(1998,1999,2006)[3- 5]、Kelejian等人(2004)[6] 在SD模型方面做过深入的研究。具体来说,时空模型可能指SPD模型也有可能指SDPD模型。SPD模型的数据相比SD模型数据还在不同时间被观测,Anselin(1988)[6]首先研究SPD模型。Baltagi等人(2003) [7]推导了空间误差自相关的面板数据回归模型的几种拉格朗日乘子检验。Lee和Yu (2010b) [8]研究了具有固定效应和空间扰动相关的空间自回归模型的拟极大似然估计的渐近性质。最近的进展是将SPD模型扩展为空间动态面板数据(SDPD)模型,即添加时间滞后项以说明不同个体之间的序列相关性。Yu等人[9]研究了具有固定效应的空间动态面板数据模型,并得到当个体数量和时间周期都很大时估计量的拟极大似然估计的渐近性质。此外,Baltagi等人(2007b) [10]考虑各空间单元具有时间序列相关和在各时间点存在空间依赖性的特点的空间面板数据回归模型。此外,该模型还利用随机效应允许空间单元的异质性,然后对该面板数据回归模型进行拉格朗日乘数检验。Kapoor等人(2007) [11]考虑了一个误差项在空间和时间上都是相关的面板数据模型。为了允许扰动项和其他随机分量中存在不同的空间效应, Anselin(2001) [13]通过允许空间面板数据模型具有动态特征,将空间动态模型分为四类,即如果只考虑空间时间滞后,则为“纯空间递归”;如果包括个体时间滞后和空间时间滞后,则称为“时空递归”;“时间-空间同时”模型是指定了一个单独的时间滞后和一个同期的空间滞后;如果把所有形式的滞后都包括在内,则是“时空动态”模型。Elhorst(2005) [14]使用无条件极大似然法估计带有空间误差的动态面板数据模型,Mutl(2006) [15]使用三步广义矩法(GMM)研究该模型,Su和Yang(2007) [16]导出了上述模型在具有固定效应和随机效应两种情况下的估计量的拟极大似然估计。目前大多数时空模型文献大都需要会指定相关的空间权重矩阵 [17],考虑到当空间权重矩阵形式设定错误时,模型的解释性变得极为不可靠,预测能力也大大降低。所以应用Ma等人[17]提出的更为一般的时空自回归模型来进行实例分析。
1 模型介绍
Ma等人[17]提出的一般时空自回归模型同样属于SDPD模型。Lee和Yu(2010a)[12]首次总结有关文献,并给出SDPD模型的一般形式:
[Ynt=λ0WnYnt+γ0Yn,t-1+ρ0WnYn,t-1+Xntβ0+cn0+αtoln+Vnt,t=1,2,…T]。
他们根据[An=In-λ0Wn-1γ0In+ρ0Wn]的特征值将SDPD模型分为三类:稳定、空间协整和爆炸性情形。[γ0]只捕捉动态效应,[ρ0]捕捉时空效应。由于存在固定的个体和时间效应,[Xnt]将不包括任何时间不变或个体不变回归量。
近来,不少学者开始研究当不事先指定空间权重矩阵如何估计时空模型,即将空间权重矩阵转化为带估的时空系数矩阵。Dou等人[18]将传统的面板数据的时空自回归模型扩展到允许每个位置(或面板)的标量系数都彼此不同的情形。为了克服模型中固有的内生性,他们将最小二乘估计应用于Yule-Walker方程。在平稳过程和[α-]混合过程的设置下,在样本大小和位置(或面板)数量都趋于无穷大的情况下,建立了估计量的渐近理论。Guo等人[19]研究了一类有带状系数矩阵的向量自回归模型。该设置代表了高维时间序列的一种稀疏结构,但其隐含的自协方差矩阵不是带状的。当时间序列的组成部分被适当排序时,该稀疏结构也具有实际意义。他们建立了估计的带状自回归系数矩阵的收敛速度,还提出了一个确定系数矩阵中带宽度的贝叶斯信息准则,该准则被证明是一致的。他们通过研究带向量自回归过程的自协方差函数的近似带结构,构造了自协方差矩阵的一致估计。Gao等人[20]提出了一类新的时空模型,其中自回归系数矩阵是完全未知的,但假设是带状的,即非零系数只出现在主对角线周围的窄带内。这避免了主观地指定空间权重矩阵的困难。该设置仅指定相邻位置的自回归。其思想基于这样一个事实:在许多实际情况中,从邻近地点收集信息就足够了,从更远地点收集的信息就会变得多余。由于空间自回归模型的内生性,他们在Dou等人[18]研究成果的基础上采用了一种基于Yule-Walker方程的廣义矩估计方法。此外,他们还研究了基于多个Yule-Walker方程的参数估计。当维数(即节点的数量)与样本大小(即观察到的时间序列的长度)一起发散时建立了估计的渐近性质。
在最新的研究中,Ma等人[17]认为时空模型中空间权重矩阵应该被估计出来,而非事先主观给定。因为当空间权重矩阵形式设定错误时,模型的解释性变得极为不可靠,预测能力也大大降低。另一方面哪种权重矩阵是最好的选择并不总是显而易见的,因此,事先指定空间权重然后产生的模型可能会失去适应底层空间依赖结构的能力。为此,Ma等人[17]提出了高维时空模型的一般形式,在此,空间权重矩阵转化为带估的时空系数矩阵。他们提出了一种向前向后搜索算法来估计时空系数矩阵结构,并引入了机器学习中的Bagging 方法来改进基于Yule-Walker方程的广义矩估计方法,并探讨了相应的理论性质。他们把该方法应用到社交网络数据中来帮助构造更加清晰的社交网络结构。
本文的实例数据来自1963—1992年美国的10个州的香烟需求数据。相关数据可在网站(https://www.regroningen.nl/elhorst)查询。而在相关文献中对这一数据集的统计建模与推断都会提前设定空间权重矩阵。所以本文考虑在这一数据集的统计分析中将空间权重矩阵转化为带估的时空系数矩阵,应用Ma等人[17]提出的一般时空模型,做出相关的统计推断与预测。结果也表明Ma等人[17]提出的一般时空自回归模型对该香烟需求数据的建模较为贴切。
2 模型分析
由于实例分析的需要,首先引入Ma等人[17]提出的一般时空模型:
[yt=Ayt+Byt-1+xtβ+εt]。 (2.1)
其中,[yt=y1,t,y2,t,…yp,tT]表示在时刻[t]从p个位置(或节点)收集的观测值,[εt=ε1,t,ε2,t,…εp,tT]满足条件[Eεt=0],[varεt=Σε],和[covyt-j,εt=0j≥1],[Σε]是未知正定矩阵。[xt=x1,t,x2,t,…xp,tT∈Rp*d]为时变矩阵,[xt]为外生变量,满足[covxt,εt=0],[covxt,εt-1=0],并且[xt,yt]为严平稳过程。[xt]的第[i]行可以表示为[xi,t=xi,t,1,xi,t,2,…xi,t,dT∈Rd*1]。[β]是回归系数的[d*1]向量。假定[A=ai,j]和[B=bi,j]是[p*p]未知系数矩阵,以及[ai,i=01≤i≤p]。[A]捕获不同位置(或节点)之间的空间依赖性,[B]捕获动态空间依赖性。
为了表述方便,将Ma等人[17]的估计方法简述如下:
式(2.1)中[yt]的第[i]个分量可以分别表示为:
[yi,t=j=1pai,jyj,t+j=1pbi,jyj,t-1+xi,tTβ+εi,t,i=1,2,…p]。
通过两步剖面操作,上式可以转化为:
[yi,ta=aTiyi,ta+bTiyi,tb+εi,t,i=1,2,…p]。
经过整理可以得到[yi,ta=aTiyi,ta+bTiyi,tb+εi,t],其中,[yi,ta=yi,t-xi,t-1Tβa,yi,tb=yi,t-xi,t-1Tβb],[βa=Exi,t-1Txi,t-1Exi,t-1Tyi,t],[βb'=Exi,t-1Txi,t-1Exi,t-1Tyj,t-1]。
将[p]个等式整合即可得:
[yta=Ayta+Byt-1b+εt]。 (2.2)
接下来采用基于Yule-Walker方程的最小二乘估计法。令[Σ1a'=covyta',yt-1b'],[Σ0b'= covyt-1b',yt-1b'],则式(2.2)可以得到的Yule-Walker估计方程为
[Σ1a=AΣ1a+BΣ0b]。
估计方程的第[i]行可以写为[Σ1Tei=Σ1Tai+Σ0bi≡Xiθi],[i=1,2,…p]。
其中,[ei]是[p*1]的单位向量,[AT=a1,a2,…ap],[BT=b1,b2,…bp],[θi=θi,1,θi,2,…θi,τiT]是将[ai]和[bi]中非零元素叠加得到的[τi*1]向量,[Xi∈Rp*τi]是由[Σ1a'T,Σ0b']相关列组成。
其中,[Σ1a'=1nt=2nyta'yt-1b'T,Σ0b'=1nt=2nyt-1b'yt-1b'T],则广义Yule-Walker估计值[θi=XiTXi-1XiTYi,i=1,2,…p]。可以发现[θi]可以看作是加权矩阵为[W=Ip]的GMM估计器,据此再提出一种改进的估计方法,即基于Yule-Walker方程的广义矩估计法,将权重[W]分成两种情况讨论,当[p?n],权重[W=Σ0b'-1],当[p]与[n]比较靠近或者[p]大于[n]可以选择[IP]作为权重(只要[p=On])。结合所有的[θi,i=1,2,…p]就可以估计出[ai]和[bi]。进而系数矩阵[A]和[B]就可以被估计出。[β]可由[yt-Ayt-Byt-1]对[xt]进行回归估计得到。
3 实例分析
香烟需求数据来自1963—1992年美國的10个州。变量及其意义见表1。相关数据可在网站(https://www.regroningen.nl/elhorst)查询。将所有变量数据采取对数化处理后,通过绘制一阶差分后的变量间的时间序列图判断出各序列均成为平稳时间序列。时间序列图见图1,图2,图3(以两个州为例)。其中,ddmand代表一阶差分后的人均吸烟包数,ddprice代表一阶差分后的每包香烟的零售价格,ddyt代表一阶差分后的人均可支配收入。
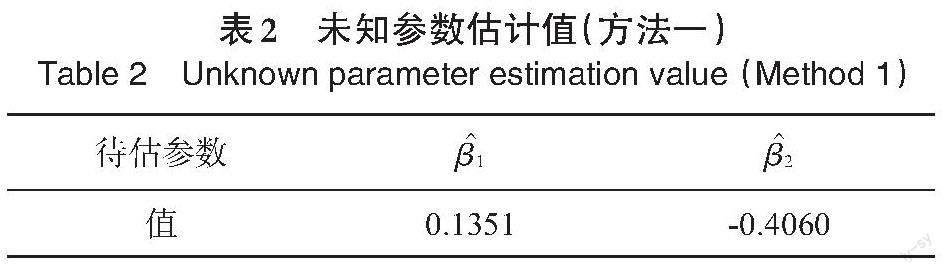
由于一阶差分后的[yt,ct,pt]均为平稳时间序列,各变量均符合应用模型的假设条件。影响抽烟需求量[ct]的影响因素设为[xt],[xt]由人均可支配收入[yt]以及每包香烟的零售价格[pt]构成。尝试借助Ma等人[17]提出的一般时空模型来拟合1963—1989年美国的10个州抽烟需求数据,估计方法分别应用基于Yule-Walker方程的最小二乘估计法(方法一)和基于Yule-Walker方程的广义矩估计法(方法二)。得到[yt]和[pt]前的系数值分别见表2和表3。估计得到的[A]捕获十个州的抽烟需求量的空间依赖性,[B]捕获十个州的抽烟需求量的时空依赖性。[A]和[B]的可视化图见图4和图5。
[待估參数 [β1] [β2] 值 0.1351 -0.4060 ][待估参数 [β1] [β2] 值 0.1350 -0.4062 ][表2 未知参数估计值(方法一)
Table 2 Unknown parameter estimation value (Method 1)][表3 未知参数估计值(方法二)
Table 3 Unknown parameter estimation value (Method 2)]
从表2和表3都可以分析出人均吸烟包数与人均可支配收入呈正相关关系,而人均吸烟包数与每包香烟的零售价格呈负相关关系。从10个州的总体情况看,每包香烟的零售价格相比人均可支配收入更能影响香烟的需求量。并可见两种估计方法得到的估计值基本一致。
图4和图5分别展示了基于Yule-Walker方程的最小二乘估计法(方法一)和基于Yule-Walker方程的广义矩估计法(方法二)得到的关于系数矩阵[A]和[B]的估计值,可见两种方法的得到的对于两个系数矩阵的估计基本一致,并且可知不同州之间的抽烟需求量会在空间和时间上互相影响,这种影响有可能是正的,也有可能是负的,影响大小也有不同。
接下来利用1963—1990年美国的10个州抽烟需求数据,估计方法采用基于Yule-Walker方程的广义矩估计法,分别进行多步预测与一步预测,来最终得到对1990-1992年各州的人均抽烟包数的预测值,并与收集的真实数据进行对比。各州的总体预测结果见表4和表5。图6给出多步预测情况下的1990-1992年各州抽烟需求量的预测结果与真实值的对比图。
表4给出多步预测的情况下1990—1992年美国10个州的人均抽烟包数的绝对预测误差以及标准差。表5给出单步预测的情况下1990—1992年美国10个州的人均抽烟包数的绝对预测误差以及标准差。容易发现单步预测相比多步预测预测效果更好,这也与直观理解相符合。从图6可以更直观看出10个州的预测效果均比较良好,并且在多步预测的情况下,对于第一年的预测效果最好,预测误差随着预测年份的递增也在增加。
4 结论
由于现有文献面对时空数据建立模型大多会事先指定空间权重矩阵,但当空间权重矩阵形式设定错误时,模型的解释性变得极为不可靠,预测能力也会在很大程度上降低,并且选择哪种权重矩阵并不总是显而易见,所以本文采用Ma等人[17]提出的一般时空模型,将其应用于1963-1992年间美国10个州的香烟需求数据进行数据分析。预测结果表明,不提前设定空间权重矩阵,应用一般时空模型直接进行分析达到了很好的预测效果。从估计未知系数的结果来看,人均吸烟包数与人均可支配收入呈正相关关系,而人均吸烟包数与每包香烟的零售价格呈负相关关系,均与现实意义相符。
参考文献:
[1] CLIFF A D. Spatial autocorrelation[R]. London:Pion,1973: 10-20.
[2] TOSTESON T D, BUONACCORSI J P, DEMIDENKO E, et al. Measurement error and confidence intervals for ROC curves[J]. Biom J, 2005,47: 409-416.
[3] KELEJIAN H H, PRUCHA I R. A generalized spatial two-stage least squares procedure for estimating a spatial autoregressive model with autoregressive disturbances[J]. The Journal of Real Estate Finance and Economics, 1998, 17: 99-121.
[4] KELEJIAN H H, PRUCHA I R. A generalized moments estimator for the autoregressive parameter in a spatial model[J]. International Economic Review, 1999, 40(2):509-533.
[5] KELEJIAN H H, PRUCHA I R. On the asymptotic distribution of the Moran I test statistic with applications[J]. Journal of Econometrics, 2001, 104(2): 219-257.
[6] ANSELIN L. Spatial Econometrics: Methods and Models[M]. Media:Springer Science & Business, 1988:25-100.
[7] BALTAGI B H, Song S H, Koh W. Testing panel data regression models with spatial error correlation[J]. Journal of Econometrics, 2003, 117(1): 123-150.
[8] LEE L F, YUB J. Estimation of spatial autoregressive panel data models with fixed effects [J]. Journal of Econometrics, 2010, 154: 165.
[9] YU J, DE JONG R, LEE L. Quasi-maximum likelihood estimators for spatial dynamic panel data with fixed effects when both n and T are large[J]. Journal of Econometrics, 2008, 146(1): 118-134.
[10] BALTAGI B H, SONG S H, JUNG B C, et al. Testing for serial correlation, spatial autocorrelation and random effects using panel data[J]. Journal of Econometrics, 2007, 140(1): 5-51.
[11] KAPOOR M, KELEJIAN H H, Prucha I R. Panel data models with spatially correlated error components[J]. Journal of Econometrics, 2007, 140(1): 97-130.
[12] YU J, DE JONG R, Lee L. Estimation for spatial dynamic panel data with fixed effects: The case of spatial cointegration[J]. Journal of Econometrics, 2012, 167(1): 16-37.
[13] ANSELIN L. Spatial econometrics, a companion to theoretical econometrics[M]. Hoboken NJ: Blackwell Publishing Ltd, 2001:310-330.
[14] ELHORST J P. Specification and estimation of spatial panel data models[J]. International Regional Science Review, 2003, 26(3): 244-268.
[15] MUTL J, PFAFFERMAYR M. The Hausman test in a Cliff and Ord panel model[J]. The Econometrics Journal, 2011, 14(1): 48-76.
[16] SU L, YANG Z. Instrumental variable quantile estimation of spatial autoregressive models[J]. Working Papers,2011,5(1): 1-30.
[17]YM A , SG B , HW C . Sparse spatio-temporal autoregressions by profiling and bagging[J]. Journal of Econometrics, 2021,232(1): 132-147.
[18] DOU B, PARRELLA M L, YAO Q. Generalized Yule–Walker estimation for spatio-temporal models with unknown diagonal coefficients[J]. Journal of Econometrics, 2016, 194(2): 369-382.
[19] GAO Z, MA Y, WANG H, et al. Banded spatio-temporal autoregressions[J]. Journal of Econometrics, 2019, 208(1): 211-230.
[20] GUO S, WANG Y, YAO Q. High-dimensional and banded vector autoregressions[J]. Biometrika, 2016,103(4):889-903.
Inference of a Spatio-Temporal Autoregressive Model Based on US Smoking Data
WU Yue-yi , HUANG Zhen-sheng
(School of Mathematics and Statistics, Nanjing University of Science and Technology, Nanjing 210094,China)
Abstract: In view of the establishment of most of the spatiotemporal models in the current literature, most of them need to specify the relevant spatial weight matrix in advance, and when the spatial weight matrix form is set incorrectly, the explanatory nature of the model becomes extremely unreliable, and the prediction ability is greatly reduced, a more general spatiotemporal autoregressive model is proposed to fit the US smoking demand data and make single-step and multi-step prediction, and the model converts the spatial weight matrix into a space-time coefficient matrix with estimation. The generalized moment estimation method based on Yule-Walker equation and the least squares method based on Yule-Walker equation were used to estimate the coefficient matrix, and the final results of both prediction methods showed that the modeling effect was better. In addition, the model analysis results also show that the per capita number of smoking packs is positively correlated with per capita disposable income, while the per capita number of smoking packs is negatively correlated with the retail price of each pack of cigarettes, which is consistent with practical significance.
Key words: spatio-temporal data; spatio-temporal autoregression; Yule-Walker equation; generalised moments estimation; cigarette demand
(責任编辑:马乃玉)
