2-[J#]-clean 环
2023-11-18陶丹丹殷晓斌
陶丹丹 殷晓斌


收稿日期:2023-07-13
基金项目:安徽省自然科学基金项目(2008085MA06);安徽省高校优秀青年人才支持计划项目(gxyqZD2019009).
作者简介:陶丹丹(1998—),女,安徽安庆市人,硕士研究生,研究方向为环论;通讯作者:殷晓斌(1972—),男,安徽枞阳县人,博士,教授,研究方向为同调代数与环模理论.
引用格式:陶丹丹,殷晓斌.2- J# -clean 环[J].安徽师范大学学报(自然科学版),2023,46(5):409-417.
DOI:10.14182/J.cnki.1001-2443.2023.05.001
(安徽师范大学 数学与统计学院, 安徽 芜湖 241003)
摘要:引入了2-[J#]-clean环的概念。设[R]是一个环,如果[R]中的每个元素都是一个幂等元和两个[J#(R)]元素的和,则称[R]是一个2-[J#]-clean环。本文主要研究了2-[J#]-clean环的基本性质,并考虑它与一些相关的环之间的联系。
关键词:2-[J#]-clean 环;2-clean 环;矩阵环;环扩张
中图分类号: O153.3 文献标志碼: A 文章编号: 1001-2443(2023)05-0409-09
引言
本文中的环都是指含单位元的结合环,环上的模都是酉模。设[R]为环,[Id(R)]、[N(R)]、[U(R)]、[J(R)]、[C(R)]分别表示[R]的幂等元之集、诣零元之集、可逆元之集、[R]的Jacobson 根、[R]的中心。[Mn(R)]表示环[R]上的[n]阶全矩阵环,[Tn(R)]表示上三角矩阵环。
1977年,Nicholson在文献[1]中首次提出clean的概念。称[R]为clean环,若[R]中任意元素都是一个幂等元和一个可逆元的和。1999年,Nicholson在文献[2]中引入强clean环的概念。称[R]为强clean环,若[R]中任意元素都是一个幂等元和一个可逆元的和且两者可交换。近来年,关于clean环及其推广[3-5]的研究吸引了众多学者的关注。2009年,王周和陈建龙在文献[6]中提出了2-clean环的概念。称[R]为2-clean环,若对任意[a∈R],都存在[e∈Id(R)],[u1,u2∈U(R)],使得 [a=e+u1+u2]。2010年,Chen在文[7]中提出了(强)[J]-clean环的概念。称[R]是强 [J]-clean环,若[R]中的任意元素都是一个幂等元和一个Jacobson根的和(且两者可交换)。2013年,Diesl在文献[8]中提出了诣零-clean环的概念。称[R]是诣零-clean环,若对任意[a∈R],都存在[e∈Id(R)],[n∈N(R)],使得 [a=e+n]。2017年,程瑶在文献[9]中定义了[J#(R)=x∈R|xn∈J(R),存在整数n≥1],显然[J(R)?J#(R)]。并引入强[J#]-clean环的概念。称[R]是强[J#]-clean环,若[R]中每个元素都可以表示成幂等元与[J#(R)]的元素之和且二者可交换。2020年,崔建和秦龙在文献[10]中引入了GJ-clean环的概念。称[R]是GJ-clean环,若对任意[a∈R],都存在[e∈Id(R)],[w∈J#(R)],使得[a=e+w]。为叙述方便,本文称其为 [J#]-clean环。2022年,陈蒋欢、王尧、任艳丽在文献[11]中提出了2-诣零-clean环的概念。称[R]是2-诣零-clean环,若对任意[a∈R],都存在[e∈Id(R)],[n1,n2∈N(R)],使得[a=e+n1+n2],其中元素[a]的和式分解称为2-诣零-clean分解。
受上述的启发,考虑到Jacobson根在环模论研究中的重要性,本文进一步考虑了[J#(R)=x∈R|xn∈J(R),存在整数n≥1],在 2-诣零-clean 环的基础上引入了 2-[J#]-clean 环的概念。设[R]是一个环,如果对任意[a∈R],都存在[e∈Id(R)],[w1,w2∈J#(R)],使得[a=e+w1+w2],则称[R]是2-[J#]-clean 环。如果 [e]和[w1],[e]和[w2]还满足乘法可交换性([w1],[w2]未必可交换),则称其为强2-[J#]-clean环。本文重点研究了2-[J#]-clean元及 2-[J#]-clean环的相关性质。此外,还引入了强2-[J#]-clean环和唯一2-[J#]-clean环的概念,并证明了唯一2-[J#]-clean环是强2-[J#]-clean 环,但反之未必成立。
1 2-[J#]-clean元与2-[J#]-clean环
定义 1.1 设[R]为环,称[a∈R]是2-[J#]-clean元,若存在[e∈Id(R)],[w1,w2∈J#(R)],使得[a=e+w1+w2]。称[R]是2-[J#]-clean环,若[R]中每个元素都是2-[J#]-clean元。
当[J#(R)]为环[R]的加法子集时(例如交换环),[R]是[J#]-clean环当且仅当[R]是 2-[J#]-clean环。显然, [J#]-clean 环和 2-诣零-clean 环均是 2-[J#]-clean 环。下面的例子说明反之未必成立。
例 1.2 (1)考虑环[R=M2(Z)]中的元素[1111=1001+0100+0010]为矩阵[A=1111]的一个2-[J#]-clean分解,但它没有[J#]-clean分解。
(2)设[R=Z(2)=ba∈Q|a?2Z],则[R]是局部环,易知[J(M2(R))=M2(2Z(2))],[N(M2(R))=0]。易验证元素[3223=1001+1111+1111]为矩阵[3223]的一个2-[J#]-clean分解式,但它没有2-诣零-clean分解式。
元素[x]称为[invo]元[12],如果[x2=1]。环[R]中所有的[invo]元之集记为[Inv(R)]。
命题 1.3 若环[R]中的元素[a]是2-[J#]-clean元,则下列结论成立:
(1) 任意[u∈U(R)],[u-1au]是2-[J#]-clean元;
(2) [2+a]是2-clean元[6];
(3) 若[f]是中心冪等元,则[fa]也是2-[J#]-clean元;
(4) 存在[e∈Id(R)],[f∈Inv(R)],[w1,w2∈J#(R)],使得[a=e+f+w1+w2]。
证明 因为[a]是2-[J#]-clean元,存在[e∈Id(R)],[w1,w2∈J#(R)],使得[a=e+w1+w2]。
(1)任取[u∈U(R)],于是[u-1au=u-1(e+w1+w2)u=u-1eu+u-1w1u+u-1w2u],显然[u-1eu∈Id(R)],[u-1w1u,u-1w2u∈J#(R)]。因此,[u-1au]是2-[J#]-clean元。
(2)令[u1=1+w1,u2=1+w2∈U(R)],则[2+a=e+(1+w1)+(1+w2)=e+u1+u2]是2-clean元。
(3)若[f]是中心幂等元,则[fa=f(e+w1+w2)=fe+fw1+fw2],显然[fe∈Id(R)],[fw1,fw2∈J#(R)],故[fa]是2-[J#]-clean元。
(4)[a=e+w1+w2=(1-e)+(2e-1)+w1+w2],其中[1-e∈Id(R)], [w1,w2∈J#(R)]。因为[(2e-1)2=1],故[2e-1∈Inv(R)]。结论成立。
推论 1.4 设[R]是交换环,若[a∈R]是2-[J#]-clean元,则存在[e∈Id(R)],[f∈Inv(R)],[w∈J#(R)],使得[a=e+f+w]。
证明 由命题1.3(4)的证明可知存在[e∈Id(R)],[f∈Inv(R)],[w1,w2∈J#(R)],使得[a=e+f+w1+w2]。又由[R]是交换环可知存在[w=w1+w2∈J#(R)],则[a=e+f+w]。
命题 1.5 设[R]是2-[J#]-clean环,则下列结论成立:
(1) [R]是2-clean环;
(2) 对任意[a∈R],存在[e∈Id(R)],[w1,w2∈J#(R)],使得[a=-e+w1+w2];
(3) 若[R]是2-[J#]-clean环,则对任意[a∈R],存在[e∈Id(R)],[u∈U(R)],[w∈J#(R)],使得[a=e+u+w]。
证明 (1) 因为[R]是2-[J#]-clean环,所以对任意[a∈R],有[2+a=e+w1+w2],其中[e∈Id(R)],[w1,w2∈J#(R)]。于是[a=e+(w1-1)+(w2-1)],显然[(w1-1),(w2-1)∈U(R)],故[R]是2-clean环。
(2) 因为[R]是2-[J#]-clean环,所以对任意[a∈R],有[-a=e+j1+j2],其中[e∈Id(R)],[j1,j2∈J#(R)]。于是[a=-e+(-j1)+(-j2)],令[w1=-j1,w2=-j2],显然[w1,w2∈J#(R)]。
(3)根据(2)可知对任意[a∈R],有[1-a=-e+j1+j2],其中[e∈Id(R)],[j1,j2∈J#(R)]。令[u=j1-1,w=-j2],则[a=e+(j1-1)+(-j2)=e+u+w],显然[u∈U(R)],[w∈J#(R)]。
命题 1.6 设[R]为环,若[2∈U(R)],则[R]是2-[J#]-clean环当且仅当对任意[a∈R],存在[f∈Inv(R)],[w1,w2∈J#(R)],使得[a=f+w1+w2]。
证明 ([?]) 设[R]是2-[J#]-clean环,对任意[a∈R],有[1+a2=e+j1+j2],其中[e∈Id(R)],[j1,j2∈J#(R)]。于是[a=(2e-1)+2j1+2j2],显然[2e-1∈Inv(R)],[2j1,2j2∈J#(R)]。
([?]) 若任意[a∈R],都有[2a-1=f+w1+w2],其中[f∈Inv(R)],[w1,w2∈J#(R)]。于是[a=f+12+w12+w22],其中[(f+12)2=1+2f+14=f+12∈Id(R)],[w12,w22∈J#(R)],故[R]是2-[J#]-clean环。
称环[R]为GUJ环[10],若对任意[u∈U(R)],都存在一个[b∈J#(R)],使得[u=1+b]。
命题 1.7 设[R]是GUJ环,则下列结论成立:
(1)若[R]是2-[J#]-clean 环当且仅当[R]是 2-clean 环;
(2)若[R]是2-[J#]-clean 环当且仅当对任意[a∈R],存在[e∈Id(R)],[u∈U(R)],[w∈J#(R)],使得[a=e+u+w]。
证明 (1) ([?]) 由命题1.5(1)的证明可得。
([?]) 因为[R]是2-clean环,对任意[a∈R],有[2+a=e+u1+u2],其中[e∈Id(R)],[u1,u2∈U(R)]。又因为[R]是GUJ环,所以存在[w1,w2∈J#(R)],使得[u1=1+w1,u2=1+w2],则[2+a=e+(1+w1)+(1+w2)],[a=e+w1+w2],得证。
(2) ([?]) 根据命题1.5(3)可得。
([?]) 对任意[a∈R],有[1+a=e+u+w],其中[e∈Id(R)],[u∈U(R)],[w∈J#(R)]。又因为[R]是GUJ环,所以存在[j∈J#(R)],使得[u=1+j],则[1+a=e+(1+j)+w],[a=e+j+w],故[R]是2-[J#]-clean环。
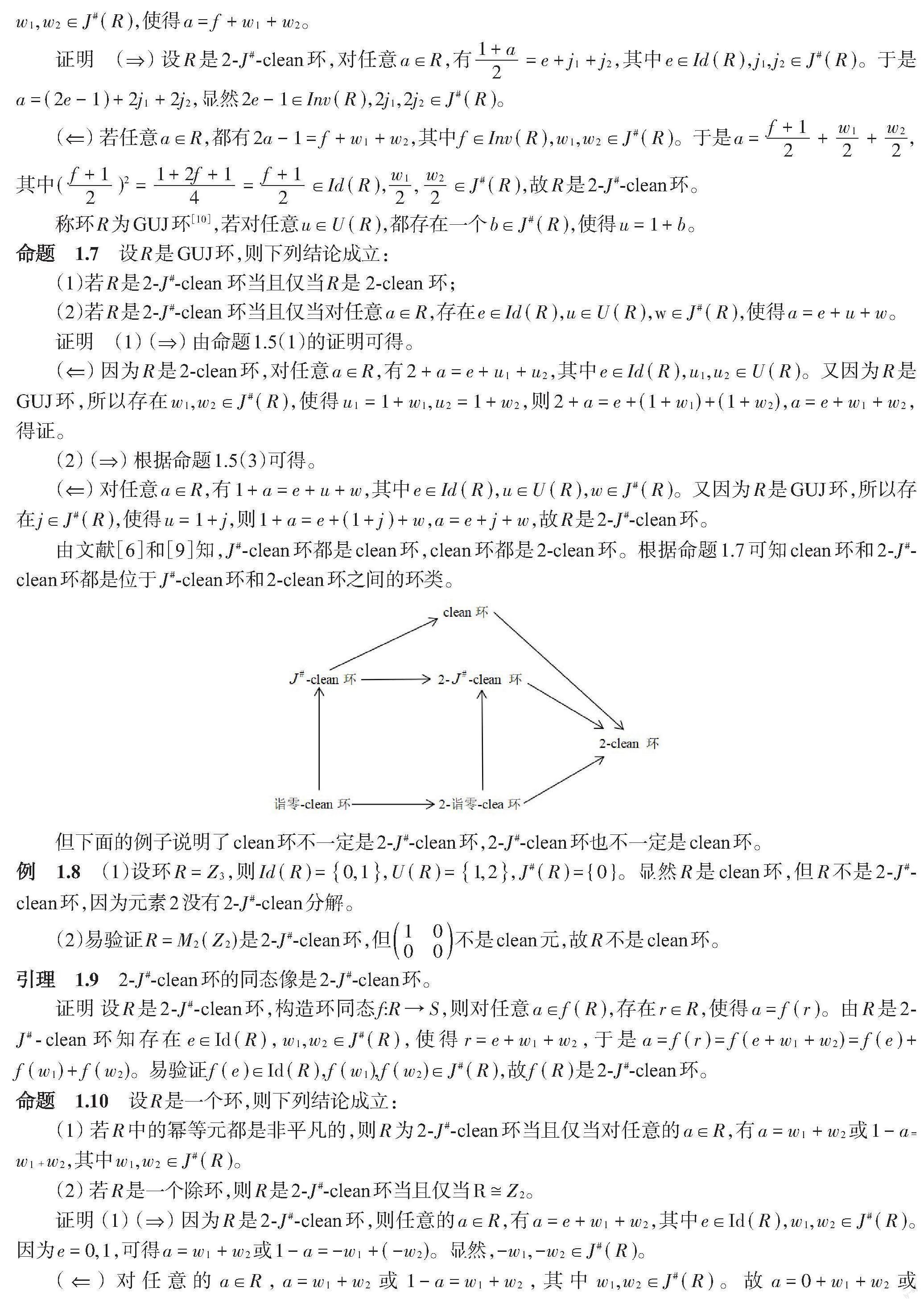
由文献[6]和[9]知,[J#]-clean环都是clean环,clean环都是2-clean环。根据命题1.7可知clean环和2-[J#]-clean环都是位于[J#]-clean环和2-clean环之间的环类。
但下面的例子说明了clean环不一定是2-[J#]-clean环,2-[J#]-clean环也不一定是clean环。
例 1.8 (1)设环[R=Z3],则[Id(R)=0,1],[U(R)=1,2],[J#(R)={0}]。显然[R]是clean环,但[R]不是2-[J#]-clean环,因为元素2没有2-[J#]-clean分解。
(2)易验证[R=M2(Z2)]是2-[J#]-clean环,但[1000]不是clean元,故[R]不是clean环。
引理 1.9 2-[J#]-clean环的同态像是2-[J#]-clean环。
证明 设[R]是2-[J#]-clean环,构造环同态[f:R→S],则对任意[a∈f(R)],存在[r∈R],使得[a=f(r)]。由[R]是2-[J#]-clean环知存在[e∈Id(R)],[w1,w2∈J#(R)],使得[r=e+w1+w2],于是[a=f(r)=f(e+w1+w2)=f(e)+f(w1)+f(w2)]。易验证[f(e)∈Id(R)],[f(w1),f(w2)∈J#(R)],故[f(R)]是2-[J#]-clean环。
命题 1.10 设[R]是一个环,则下列结论成立:
(1) 若[R]中的幂等元都是非平凡的,则[R]为2-[J#]-clean环当且仅当对任意的[a∈R],有[a=w1+w2]或[1-a=w1+w2],其中[w1,w2∈J#(R)]。
(2) 若[R]是一个除环,则[R]是2-[J#]-clean环当且仅当[R?Z2]。
证明 (1) ([?]) 因为[R]是2-[J#]-clean环,则任意的[a∈R],有[a=e+w1+w2],其中[e∈Id(R)],[w1,w2∈J#(R)]。因為[e=0,1],可得[a=w1+w2]或[1-a=-w1+(-w2)]。显然,[-w1,-w2∈J#(R)]。
([?]) 对任意的[a∈R],[a=w1+w2]或[1-a=w1+w2],其中[w1,w2∈J#(R)]。故[a=0+w1+w2]或
[a=1+(-w1)+(-w2)]。因此,[R]是2-[J#]-clean环。
(2) ([?]) 设[R]是一个除环,则[Id(R)=0,1],[J#(R)={0}]。又因为[R]是2-[J#]-clean环,则对任意的[a∈R],[a=0]或1。故[R?Z2]。
([?]) 设[R]是一个除环,若[R?Z2],显然[R]是2-[J#]-clean环。
推论 1.11 设[R]是一个局部环。若[R]是2-[J#]-clean环,则对任意的[a∈R],有[a∈J(R)]或[1-a∈J(R)]。
证明 因为[R]是局部环,则[RJ(R)]是除环。根据引理1.9可知[RJ(R)]也是2-[J#]-clean环。又根据命题1.10(2)可知[RJ(R)=0,1],所以对任意的[a∈R],[a=0,1],即[a∈J(R)]或[a∈1+J(R)]。
推论 1.12 设[R]是一个局部环。若[R]是2-[J#]-clean环当且仅当[R]是[J]-clean环。
证明 ([?]) 由推论1.11可知对于任意[a∈R],有[a∈J(R)]或[1-a∈J(R)]。显然[a]是[J]-clean的,故[R]是[J]-clean环。
([?]) 显然。
命题 1.13 对任意的[i∈1,2,…,n],设[Ri]是一族环,则直积[R=i=1nRi]是2-[J#]-clean环当且仅当每个[Ri]是2-[J#]-clean环,其中[i∈1,2,…,n]。
证明 ([?]) [Ri]作为 [R=i=1nRi],[i=1,2,…,n]的同态像,根据引理1.9可知[Ri],[i=1,2,…,n]是2-[J#]-clean环。
([?]) 任取[x=(a1,a2,…,an)∈R]。对任意的[i∈1,2,…,n],由[Ri]是2-[J#]-clean环知存在[ei∈Id(Ri)],[w1i,w2i∈J#(Ri)],使得[ai=ei+w1i+w2i]。令[e=(e1,e2,…,en)],[w1=(w11,w12,…,w1n)],[w2=(w21,w22,…,w2n)],则[e∈Id(R)],[w1,w2∈J#(R)]且[a=e+w1+w2],故[R]是2-[J#]-clean环。
命题 1.14 设[R]是一个环,[I]是[R]的一个理想且[I?J#(R)?C(R)]。若幂等元模[I]可提升,则[RI]是2-[J#]-clean环当且仅当[R]是2-[J#]-clean环。
证明 ([?]) 对任意的[a∈R],由[RI]是2-[J#]-clean环知存在[e0∈Id(RI)],[w1k1,w2k2∈J(RI)],使得[a=e0+][w1]+[w2],其中[k1,k2]均为正整数。因为幂等元模[I]可提升,所以存在[e∈Id(R)],使得[e=e0]。再由[I?J#(R)]是[R]的一个理想可知有[w1,w2∈J#(R)],使得[wi=wi,i=1,2],则[a=e+w1+(w2+r)],其中[r]是[I]中的某个元素。又因为[I]是中心的,于是[w2+r∈J#(R)],所以[R]是2-[J#]-clean环。
([?]) 由引理1.9可得。
环[R]是[exchange]环[1],若[RJ(R)]是正则的且幂等元模[J(R)]可提升。
推论 1.15 设[R]是一个[exchange]环,[I]是[R]的一个理想且[I?J#(R)?C(R)],则[RI]是2-[J#]-clean环当且仅当[R]是2-[J#]-clean环。
证明 由[1,推论2.4]和命题1.14可知。
2 2-[J#]-clean环的扩张
定理 2.1 设[R]为环,[R[x]]是[R]上的多项式环。若[R[x]]是2-[J#]-clean环,则[R]也是2-[J#]-clean环。
证明 由引理1.9可知[R]是2-[J#]-clean环。
推论 2.2 若[R]是交换环,则[R[x]]一定不是2-[J#]-clean环。
证明 由[R]是交换环立即可知[J#(R)=J(R)],[Id(R[x])=Id(R)]。假设[R[x]]是2-[J#]-clean环,则[x=e+w1(x)+w2(x)],其中[e∈Id(R)],[w1(x),w2(x)∈J#(R[x])=J(R[x])]。设[w1(x)=a0+a1x+…+anxn],[w2(x)=b0+b1x+…+bmxm],其中[aini=1, bjmj=1∈J#(R)=J(R)]。代入展开得一次项系数[1=a1+b1],于是[a1=1-b1∈U(R)],而[a1∈J#(R)],矛盾,故[R[x]]一定不是2-[J#]-clean環。
设[R]是一个环,[s∈C(R)],集合[Ks(R)= (aij)∈M2(R)|aij∈R, i,j=1,2]关于矩阵加法和如下定义的乘法:[abcda bc d=aa+sbcab+bdca+dcscb+dd],作成一个环。
命题 2.3 设[R]是一个环,[s∈C(R)]。若[R]是2-[J#]-clean环,则[Ks(R)]也是2-[J#]-clean环。
证明 任取[abcd∈Ks(R)],由[R]是2-[J#]-clean环知存在[e1,e2∈Id(R)],[w1,w2,w3,w4∈J#(R)],使得[abcd=e100e2+w1b0w2+w30cw4]。易验证[e100e2∈Id(Ks(R))]。设存在[m1,m2,m3,m4∈N+]使得[wm11,wm22,wm33,wm44,∈J(R)],令[m=m1+m2,m=m3+m4],则
[w1b0w2m=wm1i+j=m-1wi1bwj20wm2=0],
[w30cw4m=wm30i+j=m′-1wi3cwj4wm4=0],
于是[w1b0w2,w30cw4∈J#(Ks(R))],故[Ks(R)]是2-[J#]-clean环。
若s=1,则[Ks(R)=M2(R)],于是有
推论 2.4 设[R]是 2-[J#]-clean环,则[M2(R)]也是 2-[J#]-clean 环。
定理 2.5 设[S]为环,[R=Mn(S),n≥2]。则任意矩阵[A∈R]可以表示为一个对角矩阵与一个2-[J#]-clean元的和。
证明 对任意矩阵[A=(aij)∈R]。令[W1=(hij)],其中
[hij=aij, i [W2=(gij)],其中 [gij=aij, i>j0, i≤j], [A1=diag(a11,a22,…,ann)],则[W1,W2∈J#(R)],且[A=A1+W1+W2]。注意[W1+W2=0+W1+W2]为一个2-[J#]-clean元。 定理 2.6 [R]是2-[J#]-clean环当且仅当[Tn(R)]是2-[J#]-clean环。 证明 ([?]) 设[A=(aij)∈Tn(R)],其中[i≤j]。令[W=(hij)],其中 [hij=aij, i 因为[R]是2-[J#]-clean环,则对任意[i∈1,2,…,n],存在[eii∈Id(R),wii,w′ii∈J#(R)],使得[aii=eii+wii+wii]。设 [A1=diag(a11,a22,…,ann)], [E=diag(e11,e22,…,enn)], [W′1=diag(w11,w22,…,wnn)], [W′2=diag(w′11,w′22,…,w′nn)]。 则[A1=E+W1+W2],其中[E∈Id(Tn(R))]。令[W1=W+W1],[W2=W2],显然[W1,W2∈J#(Tn(R))]。故[A=A1+W=E+W1+W2+W=E+W1+W2]是一个2-[J#]-clean分解。故[Tn(R)]是2-[J#]-clean环。 ([?]) 显然。 命题 2.7 设[S]为任意非零环,[R=Mn(S),n≥2],[M=ABCD∈R]。若[A]是[Mk(S)]中的2-[J#]-clean元且[D]是[Mn-k(S)]中的2-[J#]-clean元,则[M]是[R]中的一个2-[J#]-clean元。 证明 设[A=E+W1+W2],[D=E+W1+W2]分别是矩阵环[Mk(S)]和[Mn-k(S)]上的2-[J#]-clean分解,其中[E∈Id(Mk(S))],[E′∈Id(Mn-k(S))],[W1,W2∈J#(Mk(S))],[W1,W2∈J#(Mn-k(S))]。则 [M=E00E+W1B0W1+w20Cw2]。 显然[E00E∈Id(R)],易验证[W1B0W1,w20Cw2∈J#(R)]。故[M]是[R]中的一个2-[J#]-clean元。 推论 2.8 设[R=Mn(S),n≥2],其中[n≥2]且[S]是任意非零环。设[A=(Aij)∈R]是分块矩阵,若方阵[Aii]是2-[J#]-clean元,则[A]是2-[J#]-clean环。 定理 2.9 设[R]是一个环,[e∈Id(R)]。若[eRe]和[(1-e)R(1-e)]都是2-[J#]-clean环,则[R]也是2-[J#]-clean环。 证明 设[f=1-e]。[R?eReeRffRefRf],任取[A=axyb∈R],由题意可知有[a=e+w1+w2∈eRe]且[b=f+j1+j2∈fRf],其中[e∈Id(eRe)],[w1,w2∈J#(eRe)],[f∈Id(fRf)],[j1,j2∈J#(fRf)]。于是 [axyb=e00f′+w10yj1+w2x0j2], 易验证[e00f′∈Id(R)],[w10yj1,w2x0j2∈J#(R)]。故[R]是2-[J#]-clean环。 推论 2.10 设[R]为环,[R]的单位元[1=e1+e2+…+en],其中[e1,e2,…,en]为[R]的正交幂等元。若对任意的[i=1,2,…,n],[eiRei]均是2-[J#]-clean环,则[R]也是2-[J#]-clean環。 推论 2.11 设[M=M1⊕M2⊕…⊕Mn]是一个模,如果对任意的[i=1,2,…,n],都有[End(Mi)]是2-[J#]-clean环,那么[End(M)]也是2-[J#]-clean环。 定理 2.12 设[R]是2-[J#]-clean环,则[Mn(R),n≥1]也是2-[J#]-clean环。 证明 设[R]是2-[J#]-clean环,考虑[R]上的矩阵环[Mn(R),n≥1]。对于任意的[i=1,2,…,n],设[eii]为第[i]行第[i]列的元素为1,其它元素都取0的矩阵,则[eiini=1]为[Mn(R)]的一组正交幂等元且[1=e11+e22+…+enn]。此时对任意的[i]都有[eiiMn(R)eii?R]是2-[J#]-clean环,由推论2.9可知[Mn(R)]是2-[J#]-clean环。 命题 2.13 设[R,S]是环,[RMS]是双模,则形式上三角矩阵环[RM0S]是2-[J#]-clean环当且仅当[R]和[S]均是2-[J#]-clean环。 证明 ([?]) 构造满同态[?:RM0S→R;rm0s→r],其中[r∈R,s∈S,m∈M]。再由引理1.9可知[R]是2-[J#]-clean环。同理可得[S]也是2-[J#]-clean环。 ([?]) 设[R,S]都是2-[J#]-clean环,任取[rm0s∈RM0S],则存在[e∈Id(R)],[w1,w2∈J#(R)],[f∈Id(S)],[j1,j2∈J#(S)],使得[r=e+w1+w2,s=f+j1+j2]。于是有 [rm0s=e00f+w100j1+w2m0j2], 其中[e00f∈Id(A)],[w100j1,w2m0j2∈J#(A)]。故[A=RM0S]是2-[J#]-clean环。 给定环[R]和一个双模[RMR],称[T(R,M)=R⊕M]是[R]通过[M]的平凡扩张,其中加法为对应加量加法,乘法定义为[(r1,m1)(r2,m2)=(r1r2,r1m2+m1r2)]。则[T(R,M)?rm0r|r∈R,m∈M]。 命题 2.14 平凡扩张[T(R,M)]是2-[J#]-clean环当且仅当[R]是2-[J#]-clean环。 证明 ([?]) 设[T(R,M)]是2-[J#]-clean环,取[I=(0,m)|m∈M],则[I]是[T(R,M)]的一个理想且[T(R,M)I?R],故[R]是2-[J#]-clean环。 ([?]) 设[R]是2-[J#]-clean环,任取[(r,m)∈T(R,M)],由条件知存在[e∈Id(R)],[w1,w2∈J#(R)],使得[r=e+w1+w2]。于是[(r,m)=(e,0)+(w1,m)+(w2,0)]。显然[(e,0)∈Id(T(R,M))],[(w2,0)∈J#(T(R,M))],下面只需证明[(w1,m)∈J#(T(R,M))]即可。设存在正整数[n],使得[w1n∈J(R)],那么计算可得 [(w1,m)2n=(w2n1,i,j≥0i+j=2n-1wi1mwj1)∈J(T(R,M))]。 故[(w1,m)∈J#(T(R,M))],所以[T(R,M)]是2-[J#]-clean环。 3 强2-[J#]-clean环和唯一2-[J#]-clean环 定义 3.1 称[a∈R]是强2-[J#]-clean元,若存在[e∈Id(R)],[w1,w2∈J#(R)],使得[a=e+w1+w2]且[ew1=w1e,ew2=w2e]。称[R]是强2-[J#]-clean环,若[R]中每个元素都是强2-[J#]-clean元。 显然,当[J#(R)]为环[R]的加法子集时,[R]是强[J#]-clean环[9]当且仅当[R]是强2-[J#]-clean环。 命题 3.2 若[R]是强2-[J#]-clean环,则[C(R)]中的元素都是[R]中的强 [J#]-clean元。 证明 对任意的[x∈C(R)],因为[R]是强2-[J#]-clean环,故存在[e∈Id(R)],[w1,w2∈J#(R)],使得[x=e+w1+w2]且[ew1=w1e,ew2=w2e]。又因为[xw1=w1x],所以[w1w2=w2w1],从而存在[w],使得[w=w1+w2∈J#(R)]。此时[x=e+w]且[ew=e(w1+w2)=(w1+w2)e=we]。故[x]是强[J#]-clean元。 推论 3.3 若[R]是强2-[J#]-clean环,则[2∈J(R)]。 证明 因为[2∈C(R)],所以由命题3.2知2是强[J#]-clean元,故存在[e∈Id(R)],[w∈J#(R)],使得[2=e+w]且[ew=we]。于是[1-e=w-1∈Id(R)?U(R)],则[1-e=1],从而[e=0],故[2=w∈J#(R)],又因为[2∈C(R)],所以[2∈J(R)]。 引理 3.4 设[R]为环,[a∈R]是一个强2-[J#]-clean元,则[annl(a)?annl(e)],[annr(a)?annr(e)]。 证明 因为[a]是强2-[J#]-clean元,则存在[e∈Id(R)],[w1,w2∈J#(R)],使得[a=e+w1+w2]且[ew1=w1e,ew2=w2e]。设[r∈annl(a)],则[ra=r(e+w1+w2)=0]。由[re=-rw1-rw2=-rw1e-rw2e=-rew1-rew2]可得[re(1+w1+w2)=0],因为[1+w1+w2=[(1+w1)+w2]∈U(R)],所以[re=0],故[r∈annl(e)]。同理可得[annr(a)?annr(e)]。 定理 3.5 设[R]为环且[f∈Id(R)]。则[a∈fRf]在[R]中是强2-[J#]-clean元当且仅当[a]在[fRf]中是强2-[J#]-clean元。 证明 ([?]) 设[a=e+w1+w2],其中[e∈Id(fRf)],[w1,w2∈J#(fRf)],且[ew1=w1e,ew2=w2e]。显然,[w?fJ#(R)f?J#(R)]。因此,[a∈fRf]是[R]中的一个强2-[J#]-clean元。 ([?]) 设[a=e+w1+w2],其中[e∈Id(R)],[w1,w2∈J#(R)],且[ew1=w1e,ew2=w2e]。因为[a∈fRf],所以 [1-f∈annl(a)?annr(a) ?annl(e)?annr(e) =R(1-e)?(1-e)R =(1-e)R(1-e) ] 因此[ef=e=fe],故[a=fef+fw1f+fw2f]。显然[fef∈Id(fRf)],[fw1f,fw2f∈], [fJ#(R)f=J#(fRf)],且[(fef)(fw1f)=few1f=fw1ef=(fw1f)(fef)],同理 [(fef)(fw1] [f)=(fw2f)(fef)]。故命题得证。 注 该定理无需引理3.4也可证得。因为[a∈fRf],故存在[r∈R],使得[a=frf],[faf=frf=a],故[a=faf]。则[a=fef+fw1f+fw2f]。 推论 3.6 设[R]为环,令[e∈Id(R)]。若[R]是强2-[J#]-clean环,则[eRe]也是强2-[J#]-clean环。 下面考虑局部环上矩阵环的强2-[J#]-clean性。 引理 3.7 设[R]是一个局部环,则[R]是强2-[J#]-clean环当且仅当[R]是强[J]-clean环。 证明 ([?]) 众所周知,当[R]是局部环时,[J#(R)=J(R)],若[R]是强2-[J#]-clean环,显然[R]是强[J]-clean环。 ([?]) 显然成立。 类似于文献[7,推论4.7]的证明方法,我们可以得到如下結论。 定理 3.8 设[R]是一个局部环,则[A∈M2(R)]是强2-[J#]-clean元当且仅当[A∈J#(M2(R))]或[I2-A∈J#(M2(R))]或[A]相似于矩阵[1+w100w2],其中[wi?J#(R)],[i=1,2]。 证明 由引理3.7可知[R]是强[J]-clean 环,再由[7,定理5.2]可知定理成立。 如果一个矩阵[A∈Mn(R)]是不可逆的,那么称[A]是一个奇异矩阵。如果一个奇异矩阵[A∈Mn(R)]满足[In-A]不可逆,那么称这个矩阵为纯奇异矩阵。 推论 3.9 设[R]是局部环,[A∈M2(R)]是一个纯奇异矩阵,则[A]是强2-[J#]-clean矩阵当且仅当[A]相似于[1+w100w2],其中[wi?J#(R)],[i=1,2]。 证明 因为[A∈M2(R)]是一个纯奇异矩阵,所以[A?J#(M2(R))],[I2-A?J#(M2(R))],由定理3.8可知推论成立。 类似于文献[13,定理3.2]的证明方法,我们可以得到如下结论。 命题 3.10 设[R]是一个局部环,[s∈C(R)]且[A∈Ks(R)],则下列命题成立: (1) [A∈Ks(R)]是强2-[J#]-clean环; (2)[A∈J#(Ks(R))]或[I2-A∈J#(Ks(R))]或[A]相似于[1+w100w2],其中[wi∈J#(R)],[i=1,2]。 证明 由引理3.7和[13,定理3.2]可得。 定义 3.11 称[R]是唯一2-[J#]-clean环,若[R]中每个元素的2-[J#]-clean分解在不考虑[w1,w2]的先后顺序下是唯一的。 下面的例子说明了2-[J#]-clean环未必是唯一2-[J#]-clean环,强2-[J#]-clean环也未必是唯一2-[J#]-clean环。 例 3.12 (1) 设环[R=M2(Z2)],显然[Z2]是2-[J#]-clean环,再由定理2.11知[R]也是2-[J#]-clean环。元素[1101]至少有两种不同的分解:[1001+0100+0000],[0010+1111+0000],所以[R]不是唯一2-[J#]-clean环。 (2) 设环[R]为模4剩余类环[R=Z4],[Id(R)=0,1],[J#(R)=0,2],显然它是一个强2-[J#]-clean环。但因为1=1+0+0=1+2+2为元素1的两种不同的2-[J#]-clean分解,所以[R]不是唯一2-[J#]-clean环。 命题 3.13 若[R]是唯一2-[J#]-clean环,则[R]中的幂等元都是中心的,即[R]是Abel环。 证明 任取[e∈Id(R),r∈R],则[e+er-ere=e+(er-ere)+0=(e+er-ere)+0+0],易验证[er-ere∈J#(R)],[e+er-ere∈Id(R)]。因为[R]是唯一2-[J#]-clean环,故[er-ere=0],[er=ere]。同理可得[re=ere],即[er=re],故[R]中的幂等元都属于[C(R)],故[R]是Abel环。 命题 3.14 设[R]是环,则下列条件等价: (1) [R]是唯一2-[J#]-clean环; (2) [R]是布尔环; 证明 (2)[?](1) 显然。 (1)[?](2) 假设[R]中存在除0以外的[J#(R)]元素[w],则[1=1+0+0=1+w+(-w)]是1的两种不同的2-[J#]-clean分解,矛盾。于是对任意的[x∈R],只有[x=e+0+0∈Id(R)]这一种2-[J#]-clean分解式,故[R]是布尔环。 定理 3.15 设[R]是环,则[R]是唯一2-[J#]-clean环当且仅当[R]也是强2-[J#]-clean环且[J#(R)=0]。 证明 ([?]) 若[R]是唯一2-[J#]-clean环,由命题3.14知[R]是布尔环。由文献[7,命题3.2]可知[R]是强[J]-clean环,显然[R]是强2-[J#]-clean环。 ([?]) 显然。 推论 3.16 设[R]是唯一2-[J#]-clean环,则下列结论成立: (1) [RJ(R)]是唯一2-[J#]-clean环且幂等元模[J(R)]可强提升; (2) [RJ(R)]是唯一2-[J#]-clean环且[R]是强clean环; (3) [RJ(R)]是布尔环且幂等元模[J(R)]可强提升。 证明 (1) 因为[R]是唯一2-[J#]-clean环,由定理3.15的证明可知[R]是强[J]-clean环且[J(R)?J#(R)=0],则[RJ(R)]是布尔环,又由命题3.14知[RJ(R)]是唯一2-[J#]-clean环。因为[R]是强[J]-clean环,由[7,定理2.3]可知幂等元模[J(R)]可强提升。 (2) 由(1)的证明和[7,命题2.1]可得。 (3) 由(1)和命题3.14可得。 参考文献 [1] NICHOLSON W K. Lifting idempotents and exchange rings[J]. Transactions of the American Mathematical Society, 1977, 229(5): 269-278. [2] NICHOLSON W K. Strongly clean rings and Fitting's lemma[J]. Communications in Algebra, 1999, 27(8): 3583-3592. [3] HAN J, NICHOLSON W K. Extensions of clean rings[J]. Communications in Algebra, 2001, 29(6): 2589-2595. [4] DANCHEV P V. On corner subrings of unital rings[J]. Internat J Contemp Math Sci, 2018, 13(2): 59-62. [5] PURKAIT S, DUTTA T K, KAR S. On m-clean and strongly m-clean rings[J]. Communications in Algebra, 2020, 48(1): 218-227. [6] WANG Z, CHEN J L. 2-clean rings[J]. Canadian Mathematical Bulletin, 2009, 52(1): 145-153. [7] CHEN H Y. On strongly J-clean rings[J]. Communications in Algebra, 2010, 38(10):3790-3804. [8] DIESL A J. Nil clean rings[J]. Journal of Algebra, 2013, 383: 197-211. [9] 程瑤. J-clean环的推广[D]. 芜湖:安徽师范大学, 2018. [10] CUI J, QIN L. Generalizations of J-clean rings[J]. Advances in Mathematics, 2020, 49(1): 29-38. [11] 陈蒋欢, 王尧, 任艳丽. 2-诣零-clean 环[J]. 山东大学学报(理学版), 2022, 57(2): 14-22. [12] DANCHEV P V. Weakly invo-clean unital rings[J]. Afrika Matematika, 2017, 28(7): 1285-1295. [13] XIANG Y M, OUYANG L Q. J-clean and strongly J-clean rings[J]. Communications in Mathematical Research, 2018, 34(3): 241-252. [14] YING Z L, CHEN J L. On UR-rings[J]. Mathematical Research & Exposition , 2009, 29(2):355-361. 2-[J#]-clean Rings TAO Dan-dan, YIN Xiao-bin ( School of Mathematics and Statistics, Anhui Normal University, Wuhu 241003, China) Abstract: This paper introduces the concept of 2-[J#]-clean rings. Let [R] be a ring, if each element in [R] is the sum of an idempotent and two [J#(R)] elements, [R] is said to be a 2-[J#]-clean ring. This paper mainly studies the basic properties of 2-[J#]-clean rings, and the relationship between it and some related rings is considered. Key words: 2-[J#]-clean rings; 2-clean rings; matrix ring; ring extension (责任编辑:马乃玉)
