模式聚类与周期分解的能耗监测及异常检测方法

金静,方园,费洋,魏源

(1.西安市轨道交通集团有限公司,西安 710018; 2.南瑞轨道交通技术有限公司,南京 210061)

0 引 言

随着智慧城轨的发展,城市轨道交通大多配备了智能电能表,获取到足够多可用于数据分析的时间序列数据。轨道交通耗电量巨大,国内主要城市平均每公里单个车辆的牵引能耗范围在1.8 kW·h～1.9 kW·h,每个车站年平均照明用电为150万kW·h～250万kW·h[1]。根据国家政策要求,减少能耗排放、降低地铁电能损耗有积极的作用。用电能耗异常检测能帮助地铁维修人员快速定位异常、进行故障检测和维修,并降低不必要的资源损耗。时间序列数据在各方面都有体现,如传感器[2]、物联网数据[3]、心电图[4]等。异常检测在设备故障诊断[5]、入侵检测[6]等方面都有应用。针对地铁能耗数据的异常检测方法也可以运用到更多的相似问题上。

时间序列异常检测是现今一个热门话题,其中一大研究课题是异常分类。文献[7]将时间序列异常分为空间异常和时间异常。文献[8]将其分为点异常、条件(上下文)异常和组异常,这也是目前在大多数论文中使用的分类方法。文献[9]提出了一种行为驱动的分类方法来进行更细致划分,此文献将异常分为点异常和模式异常(见图1),其中全局异常和上下文异常都属于点异常,模式异常又可细分为季节异常、形状异常和趋势异常。异常通常定位于特定的场景中,文中使用点异常和模式异常这种分类方法,且着重于点异常的检测,其中相比于全局异常,上下文异常检测较为困难。

图1 异常类型

由于时间序列的复杂性和多变性,异常检测尤为困难。此外,不同领域数据的多样性也增加了实现通用异常检测方法的难度。近年来,由于研究目的和异常点标记的不同,大多数检测算法是无监督的。基于简单统计的异常检测方法(如3sigma、箱型图等)计算快速、简单,但是并不适用于时间序列。子序列聚类等不一致性分析方法可以检测出子序列间的异常,但会丢失局部时间信息,难以检测出上下文异常。基于预测的方法包括统计自回归方法(如VAR、ARIMA[10])和深度学习方法(自编码器[11]、多元卷积[12]、RNN[13]等)。文献[8]总结了用于异常检测的深度学习框架并将其分为三类:用于一般特征提取的深度学习、用于正态性表示的学习和端到端异常评分学习。深度学习方法中模型准确性受异常值影响较大,需要正确的训练数据。文献[14]提出一种基于时间序列相似性的统计方法ESD(extreme studentized eeviate)。在此基础上,文献[15]提出S-ESD(seasonal ESD)和S-H-ESD(seasonal hybrid ESD)算法,利用季节分解来搜索异常。然而异常值的存在会影响分解后当前季节分量和邻居季节分量,季节曲线有向周围季节靠拢的趋势,正常值会被误判为异常值。

异常检测是一个复杂的问题,具有异常未知、异常不规则、类别不平衡、异常类型不同等特点[8]。为解决上述问题,文章将时间序列异常检测算法和聚类相结合[16-17]。聚类是一种无监督算法,可以分为基于划分的方法(K-means[18-19]、K-shape[20]等)、基于模糊的方法[21]、基于密度的方法(DBSCAN,density-based spatial clustering of applications with noise[22])、基于层次的方法等。其中K-means的广泛应用得益于其计算的简单快速,但需要给出聚类的数量,初始聚类中心点的选取也会影响聚类结果,并且基于划分的算法受异常值的影响较大。DBSCAN可以划分出边缘点,对异常点具有鲁棒性,但该方法对超参数有很大的依赖性,需要设置聚类半径和最小聚类数。此外,在计算过程中可能会将多个聚类合并为一个聚类,这是该算法的优点,而在缺乏细致调参的情况下也是算法的不足。密度峰值聚类算法(density peaks clustering,DPC)[23-24]通过计算获取数据的密度峰值点,适用于文中的情况。

除了一般时间序列特征外,地铁能耗数据还具有以下特点:

1)数据复杂多变且随机性大,除节假日影响外还与当日的天气、周围是否有大型赛事、是否有交通管控等多种因素有关;

2)数据具有一定的季节性,可以表现为天、周、月、季度、年周期性;

3)随着日升日落季节气候的变化,周期会沿着时间方向有一定的前后推移;

4)某些特定周期模式的出现并不连续,具有稀疏性和偶发性。

地铁能耗异常检测需要满足的要求如下:

1)尽可能多地检测出点异常。对于模式异常,若只在上下文显示异常而全局存在相同模式,则不认为是异常;

2)减少假阳性误报率;

3)某些特殊日期会有提前开站和延迟关站的情况,这不应被视为异常。

针对上述问题,文章提出了基于模式聚类与周期分解的能耗异常检测方法,使用子序列密度峰值聚类划分相似模式簇集,减少检测的假阳性;分别在聚类簇中使用S-H-ESD检测异常,在重构误差基础上计算异常分数,用以辅助异常评判,提高检测的准确性。实验结果表明,所提算法得到了较为理想的效果,能够实现复杂周期数据的异常检测。

1 时间序列聚类

在原始数据上寻找异常时,由于周期模式不同,相同波动值的小异常在低量级上更容易被观测到,但是在全局大数据量背景下容易被忽略。若按原始数据大小为基准判断异常程度,则会放大低量级上的异常,而大量级上实际大变化值的异常程度会降低。在这种权衡下,先对时间序列进行模式聚类较为有效。

1.1 密度峰值聚类算法

密度峰值聚类算法根据数据的聚集程度将数据分为三种类型:峰值点、异常点和普通点。该算法基于两个假设:一是聚类中心相距较远;二是聚类中心的局部密度大于相邻区域。关键计算分为局部密度ρ和相对距离δ两个步骤。总步骤如下:

1)计算出各个点间的二维距离矩阵。

2)计算局部密度ρ。

对于文章的离散数据,局部密度可用截断距离范围内点的个数表示。

ρi=∑i≠jχ(dij-dc)

(1)

式中dij为点i到点j的距离;dc为给定的截断距离;χ为一个二值函数,表示为:

(2)

3)计算相对距离δ。

(3)

若当前点为局部密度最大值,则相对距离为当前点到最远点的距离;否则相对距离为局部密度大于当前点中与当前点最近的距离。

4)找聚类中点。

根据步骤2)和步骤3)得到的结果,可以画出横纵坐标分别是局部密度和相对距离的二维决策图。其中,聚类中心有较大的局部密度和相对距离,在决策图的右上角;离群点局部密度较小但有较大的相对距离,在图的左侧。根据相对距离的计算(式(3))可以看出,局部密度最大点的相对距离较其它点有较大飞跃,选择斜率递减的递增函数来处理相对距离,在此使用负指数幂函数y=x-2。将处理后的局部密度和相对距离的乘积f(式(4))作为评判标准,数值越大,聚类中心点的可能性就越大;数值越小,极有可能是异常点。

(4)

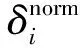
5)聚类划分。

根据计算的聚类中点和截断距离划分聚类簇有多种方法:使用广度优先搜索划分聚类簇,将相连聚类划分为一个簇;根据点与聚类中心的距离直接划分簇,文中采用这种方法。

1.2 距离度量

欧几里得距离[25]是最经典、最常用的聚类度量方法,但它在高维数据上表现效果不佳。适用于计算高维数据相似度的距离度量包括余弦相似度、互相关(cross-correlation function,CCF)、Pearson相关系数[26]等,其中余弦相似度不考虑数据值的大小,而偏重于关注数据的变化。

对于数据偏移,一种方法是使用具有动态矫正的距离公式,如动态时间规整DTW(dynamic time warping)[27],这种方法适用于横向拉伸数据的矫正,但计算复杂度较高;另一种方法是公式中加入偏移变量,将原始距离计算变为循环对齐的距离计算,这种方法适用于数据的整体相位偏移。由于数据偏移较小,文中采用改进的基于形状的距离SBD(shape-based distance)即循环互相关方法进行距离度量。循环方法保持一个序列静止,另一个序列首尾相连沿顺时针或逆时针方向转动,如图2所示,i和-i时刻的序列首位分别为yi和yd-i+1。

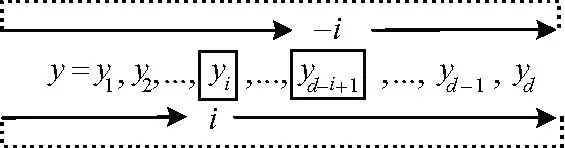
图2 循环序列

改进的SBD方法得到的序列距离表示为:

(5)

式中d为数据维度,使互相关函数SBD取最小值的i是相位偏移距离。

2 时间序列异常检测与S-H-ESD算法

为了充分利用序列的时间信息,文章使用S-H-ESD检测聚类簇内的异常。S-H-ESD是一种基于统计分析模型的轻量级计算方法,它不需要标签学习且计算速度快。

2.1 S-H-ESD算法

S-H-ESD是ESD方法的改进,使用STL(seasonal trend decomposition procedure based on loess)周期分解。STL将时间序列数据Y分解为三部分:季节分量(seasonal)、趋势分量(trend)和余项(residual),适用于多周期循环数据。季节分量表示数据的周期性,趋势分量是数据整体的趋势变化,余项则是数据扰动。用中位数替代趋势分量得到修改后的余项公式Rd,如下所示:

Y=S+T+R

(6)

Rd=Y-S-median(Y)

(7)

中位数较均值和方程对异常值具有鲁棒性,S-H-ESD使用绝对值偏差中位数(MAD,median absolute deviation)来解决异常数据敏感问题。

(8)

式中c为高斯分布中置信度为0.75的左单侧置信上限。

在每一轮中选取与中位数偏差最远的余项作为异常候选值,并从现有数据中删除当前点。

(9)

式中Rdi为第i轮(i=1,2,3…)剩余的余项数据。

为了判断当前点是否为异常,根据置信度∂计算临界值λ。

(10)

式中ppfT(1-p,n)是显著性水平为p、自由度为n的t分布的左单侧置信上限。若Ri大于临界值,判定该点异常。

算法流程总结如下:

1)输入最大异常个数M和置信度∂;

2)STL将原数据分解为季节、趋势和余项分量;

3)根据式(7)计算得到修改后的余项Rd;

4)根据式(8)和式(9)计算剩余数据MAD和与均值偏差最远的余项Ri,并将Ri从数据中删除;

5)根据式(10)计算剩余数据临界值λi,若Ri>λi则该点为异常点;

6)当迭代次数达到M时停止,否则转到步骤4)重复上述操作;

7)输出异常点序列。

2.2 异常评分

S-H-ESD通过动态置信度选出异常偏差高的数据,也可使用下述评分函数辅助异常值筛选。

1)KNN评分。

最邻近结点算法(K nearest neighbors,KNN)根据相邻点的距离和状态在每个聚类簇内评价异常值的异常程度,以S-H-ESD余项大小作为距离标准,相邻点若为异常则状态为积极,否则为消极。对每个异常点,分别找距离最近的k个点计算得分:

(11)

式中d为距离。若相邻点为异常则加上得分,否则减去得分,最终得分越大表示异常程度越大。

2)高斯尾部概率规则。

高斯尾部概率规则[7](Gaussian tail probability)使用标准正态分布的右尾概率函数Q来评判异常程度,该方法可以根据异常偏差(即余项)从全局数据中找出短时间内连续出现大量异常的情况赋予高得分。

(12)

式中μw是窗口大小为w的偏差均值,μW和σW是窗口大小为W的偏差均值和方差,w<

3 评价指标与数据

3.1 聚类评价指标

聚类使用无标签评判指标,根据数据本身的聚合程度评判聚类效果,包括轮廓系数和Calinski-Harabaz(CH)[28]。轮廓系数根据簇内点距和簇间点距各代表的聚合度和分离度评判结果好坏,取值范围为[-1,1],结果越接近1效果越好。CH计算簇内协方差的数值,数值越大聚类效果越好。

3.2 异常检测评价指标

异常检测可看作异常二分类问题,根据分类混淆矩阵采取如下评价标准:

1)查全率(recall)。

(13)

2)查准率(precision)。

(14)

为了减少地铁能耗异常的误报率,权衡R和P,在保证查准率的前提下,力求最大的查全率,文章增加Fβ评价指标:

(15)

式中β<1,优先保证查准率,文中β设为0.8。

3.3 数据集

时间序列数据F=[s1,s2,...,sd],si对应i时刻数据,d为序列长度。序列中的点值为增量数据,是单位时间左开右闭区间中数据的累计值,并以区间左侧时间为当前坐标。文章对4个地铁站进行采样,且每个地铁站采样四组能耗数据(共16组),以此展开研究。

实验使用2021年7月—2022年1月厦门某地铁线路上4个站点的能耗数据,包括两个大客流量换乘车站和两个非换乘车站。数据为24小时累计能耗数据,时间颗粒度为1小时,共有215天。

根据经验,实验标注了符合预期的异常数据,并选取四个与季节相关变化较大的数据序列,分别是牵引能耗、公共区域照明能耗、通风空调能耗和电扶梯能耗。

4 实验分析

4.1 模式聚类实验

在聚类前,为了防止异常值对距离计算的影响,对数据使用基于最小二乘法的Savitzky-Golay平滑滤波[29]。图3是牵引用电使用DPC的模式聚类结果。其中图3(a)是原始数据直接聚类后的结果,图3(b)是对原始数据使用SBD循环相位矫正后再聚类的结果。实验选取两个聚类中点划分簇集,在图3中用纯黑色点线标出。可以看出,虽然有相位偏移影响,实验使用的聚类方法仍能找到相同的聚类中点,并且通过相位矫正后数据聚集程度更高,能够实现更好的聚类效果。

图3 聚类结果

从图3中看出,地铁从开站到关站基本处于高能耗状态,凌晨处于低能耗状态或停机状态;高低能耗间有大约两小时的过渡期;大部分能耗数据在5:00左右开始上升,在0:00左右趋近于0;少部分数据(2.3%)工作时间在6:00—次日1:00,有1小时的偏移。通过循环距离可以矫正相位偏移,从得到的二分类结果中可以看出第一种能耗模式最大值出现在早高峰和晚高峰时段;第二种模式在高低能耗状态基本稳定,未见太大的能耗跳跃。

分别对16组地铁能耗数据聚类与DBSCAN、K-means对比,取结果的平均值见表1。

表1 聚类结果对比

从表1中可以看出,文中的方法在照明、通风空调和电扶梯能耗上有较高的轮廓系数,在牵引和照明能耗上有较高的CH值,展现很好的聚类效果。与照明和电扶梯能耗相比,牵引能耗和通风空调能耗值更大,数据更有规律性,因此整体聚类准确度更高。

表1中序号1为牵引能耗;2为公共区域照明能耗;3为通风空调能耗;4为电扶梯能耗。

4.2 异常检测

S-H-ESD设∂置信度为0.04,最大异常点比例为5%。分别对原始数据和经过模式聚类后的数据使用S-H-ESD算法,得到的重构结果如图4所示。原始数据和重构数据的差为S-H-ESD中的分解余项,即数据扰动,数据扰动越大则表示数据异常程度越大。图4(b)数据以虚线为界分前后两个模式簇,可以看出,直接周期分解原始数据在不同模式交界处有较大的重构误差,而通过聚类后的重构数据更加贴合原始数据,表现数据周期波动的效果更好。

图4 有无聚类的数据重构结果对比

分别对每份聚类数据使用S-H-ESD,并综合聚类重构误差整体评判数据的异常程度。图5是牵引用电的异常结果。

图5 牵引能耗异常检测结果

可以看出原始数据的波动较大,模式较为多变。根据模式聚类后分解得到的重构误差可以使用ESD筛选得到三处异常,第一处异常是在高峰期的突然置零,这可能是传输过程故障导致的数据丢失;第二处是突起的峰值点,为全局点异常;第三处是晚高峰时期的一段低能耗值。与双侧滑动窗口、线性自回归模型(AR)、自回归移动平均模型(ARIMA)和无聚类S-H-ESD结果作比较,评价指标平均值如表2所示。

表2 异常检测实验结果的评价指标

可以看出,本文提出的方法有较高的Fβ值,在查全率较高为0.798时可达到0.813的查准率,在地铁能耗的实际应用中效果更好。

5 结束语

文章使用模式聚类和周期分解相结合的方法检测地铁能耗数据的异常,只在相同周期模式上考虑不同异常情况,屏蔽不同模式数据间的影响。DPC能够筛选出合适的聚类中心点,根据此得到的聚类结果能更好反应数据间模式关系。S-H-ESD在聚类基础上检测出异常,与多种方法对比得到了较为理想的效果,适用于复杂周期模式的异常检测。

该方法应用于离线数据,还有进一步改善的空间:将检测方法运用到流数据上是今后可以继续深入研究的方向。新到达的数据需要在每个聚类中都为异常才可判定为异常点,或自成一个新聚类。提供异常解释算法,方便点对点错误纠察,减少误报率。