基于分组策略的多目标三维装箱算法
2023-11-18张长勇吴刚鑫
张长勇,吴刚鑫
自动化与智能化技术
基于分组策略的多目标三维装箱算法
张长勇,吴刚鑫
(中国民航大学 电子信息与自动化学院,天津 300300)
针对现有三维装箱算法优化目标单一、优化效率低的问题,提出适用于求解大规模货物装载问题的多目标装箱算法,以提高装箱规划效率,确保货物运输安全。考虑5种现实约束条件,以体积利用率和装载垛型重心偏移量为优化目标,建立多目标货物装载优化模型。采用拟人式装箱对货物进行预分组,减小决策空间,然后结合分组信息与装箱算法生成初始解;引入数据驱动的装箱交叉算子提高算法收敛性;设计多策略变异算子提高算法结果的多样性。以公共数据集和真实航空货物数据作为实验数据进行实验。实验结果表明,在满足多种约束条件下,集装箱装载强异构货物平均体积利用率达到92.0%,重心位置空间偏移从20 cm减少到7.5 cm,并且算法运行时间减少了73.5%。本文所提算法应用于求解大规模多目标三维装箱问题,提高了装箱质量和效率,可为三维装箱算法的工程应用提供参考。
三维装箱;多目标优化;组合优化;多变异策略
近年来,随着我国的经济总量和对外贸易水平的逐步提升,货物运输量逐年增加。货物装载是物流运输中的关键一环,货物装载自动化、智能化可以提高物流综合服务质量,促进国民经济发展。三维装箱问题是实现货物装载自动化的关键之一,对提高货物运输效率,保证货物装载质量至关重要。
三维装箱问题是解空间庞大的NP-Hard问题。为了得到近似最优解,极点法、砌墙法、中心骨架法、三空间分割法、空间重组、拟人法等构造性算法利用装载经验优化装箱布局,适用于解决货物异构性较低、装箱约束条件少的装箱问题[1-2]。随着装箱问题的发展,研究者开始考虑多种复杂的现实约束[2-3],并利用蚁群算法、化学优化算法[4]、遗传算法[5]以及一些混合邻域搜索算法[6-9]求解装箱问题,此类算法一般先利用构造性算法生成初始装载布局方案,再经过邻域搜索算法优化布局方案,使较复杂的装箱问题能够得到近似最优解。由于考虑单一目标的装箱算法解决多样的装箱场景较为困难。Trivella等[10]设计了一种考虑负载平衡和装箱数量的多目标三维装箱算法。Erbayrak等[11]提出一种以同批货物完整和负载平衡为目标的混合整数模型。由于多目标三维装箱问题的目标空间和决策空间更加庞大,使用构造性算法和数学模型求解多目标装箱问题仅能提供可行解,无法找到近似最优解。赵向领等[12]提出了一种基于改进遗传算法的多目标飞机配载模型,有效平衡了业载量和重心偏移量2个优化目标。近年来有学者开始将多目标进化算法引入装箱问题[13]。为了提高多目标进化算法寻优能力和保持解集的多样性,很多学者对进化算法进行了改进,如侯莹等[14]设计了一种数据驱动选择策略的差分进化算法,有效提升了算法求解复杂多目标问题的寻优效率。Takagi等[15]提出了一种基于权重自适应的分解多目标进化算法,通过不同子问题之间的欧式距离判断解的相似程度,并据此来调整解集的分布。
多目标进化算法的发展对解决多目标三维装箱问题具有借鉴意义。本文以体积利用率和重心位置坐标作为优化目标,提出一种基于分组策略的多目标三维装箱算法。通过货物预分组策略和稳定性移位设计降低问题难度,设计自适应选择的装箱进化算子以加快收敛速度。利用公共数据集和真实航空货物数据验证了算法的先进性和适用性。
1 多目标三维装箱规划模型
1.1 问题描述问题
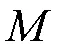
1.2 假设条件
由于货物多目标三维装箱优化问题的复杂性,为了简化数学模型,做出以下假设:
1)待装货物形状均为长方体。
2)货物在最大承重范围之内可接受多层装载。
3)待装货物重心为其几何中心。
4)集装箱中货物的码放位置不受区域的限制。
5)不考虑货物在装载过程中出现的挤压变形等。
6)货物充足,可以装满整个集装箱。
1.3 模型建立
1.3.1 符号说明
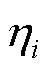
1.2.1 约束条件
根据装箱问题的现实条件,考虑约束条件如下。
1)总承载能力约束:规划装载货物的总质量不高于规定最大载重量。
2)箱体约束:货物的各个顶点均在集装箱内部。
3)不重叠约束:2个货物在、、3个平面的投影不存在2个投影面相交的情况。
4)稳定性约束:货物不可悬空,且要求每个货物下表面接触面积达一半以上。
5)货物正交放置约束:保证货物与集装箱正交或平行。
为了减少不可行解对迭代方向的影响,将约束条件分类为强约束条件和弱约束条件,其中强约束条件包括箱体约束、总质量约束、总体积约束、不重叠约束,弱约束条件有稳定性约束,顺序约束。强约束嵌入到装箱模型中,在目标函数的每次评估前对解进行约束筛选,减少了不可行解对迭代方向的影响;弱约束条件则在满足强约束条件下进行启发式设计。
1.3.2 数学模型

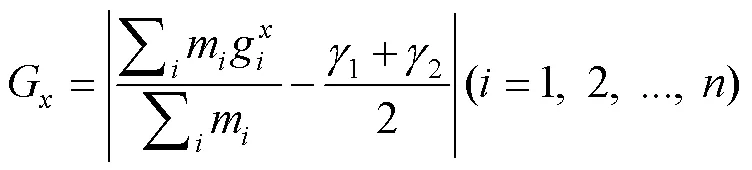
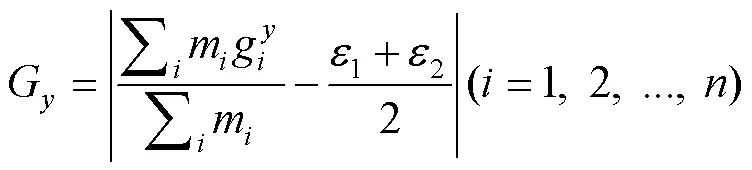
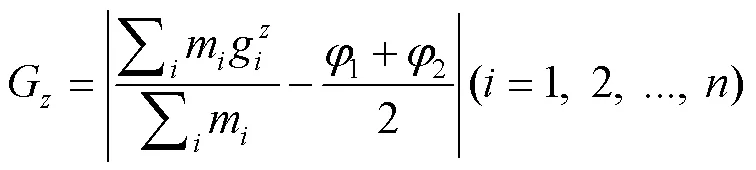

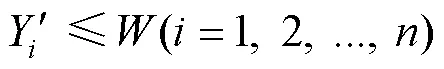



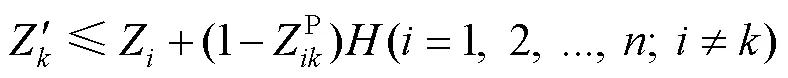
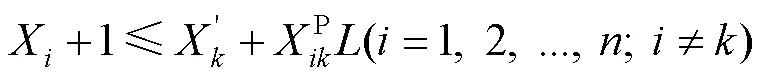

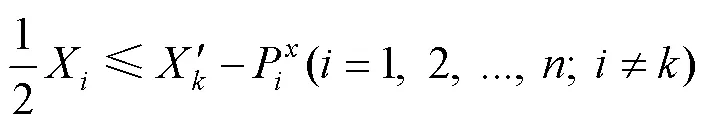


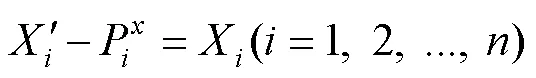


式(1)~(19)为本文所考虑的目标函数及约束条件;式(1)~(4)为目标函数,分别为装载规划的体积利用率,重心与集装箱安全重心、、方向的偏移距离;式(5)表示总承重能力约束;式(6)~(8)表示箱体约束;式(9)~(13)表示不重叠约束;式(14)~(16)表示稳定性约束;式(17)~(19)表示货物正交放置约束。
2 多目标三维装箱启发式设计
2.1 拟人式装载策略
为了使多目标装箱模型得到更优的初始解,减少产生初始解耗时,采用一种简化的拟人式装箱算法如图1所示,算法对放置点进行构建、排序、随机选取。用拟人算法对货物进行装载的优点是规则简单、装载过程可观测,并且其较差解也可以作为全局优化算法的初始解。具体算法步骤如下:
1)载入货物信息,进行货物信息预处理。
2)设定集装箱左后下角作为初始可放置点。
3)按照规则对货物排序。
4)根据约束条件检测该货物是否存在可放置点,存在可放置点,则随机选取可放置点并放置当前货物,删除已用可放置点;否则,将该货物放置待装货物栈底,返回步骤3。
5)更新可放置点及剩余货物信息。
6)判断是否有货物可装载,若是,则返回步骤3;否则,输出装载方案。
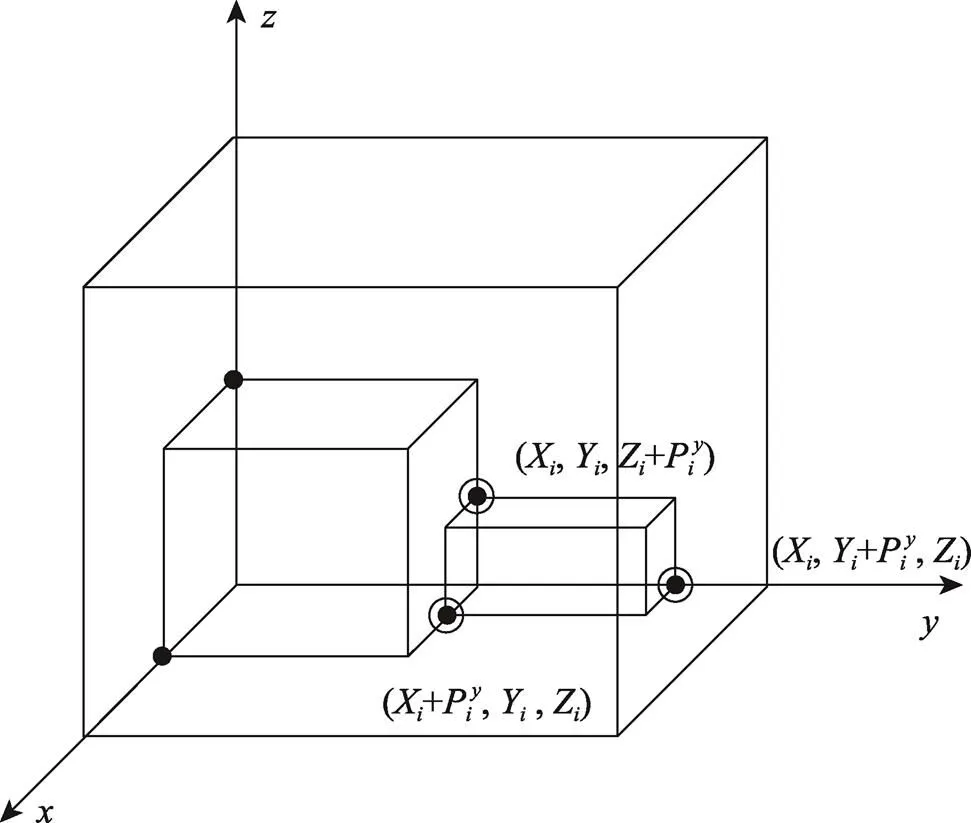
图1 拟人式装箱示意图
2.2 稳定性移位设计
考虑到约束条件较多,稳定性约束会导致得到的装箱结果出现货物悬空或者重心可变动余量较少的问题。为了使该算法在优化过程中有良好的解集筛选环境,在得到解集后对解集得到的装载结果进行进一步启发式设计。采用先越界后回归的方法保证所有货物不悬空,使最终装载方案可以最大程度安全可靠。具体流程见图2。
稳定性移位操作将在算法产生初始解以及算法的每次评价重心位置前使用,提高解的质量。保证初始解的高质量可以加快优化进程,保证最终解的高质量可以提高规划结果的安全性,避免得到货物悬空或货物容易发生偏移的装载规划。
3 基于分组策略的三维装箱算法
基于分组策略的三维装箱算法首先使用分组规则配合拟人式构造法生成初始解,然后利用多策略进化算法对多种可行方案寻优,最后得到多个目标函数均优的装载布局方案,其流程如图3所示。
3.1 编码方式


图2 稳定性移位

图3 多目标装箱算法装载流程

图4 货物放置状态示意图
3.2 分组策略及规则设计
三维装箱问题的决策空间非常庞大,因此,设计一种适用于三维装箱问题的空间降维方法对可行解的搜索有较大帮助。分组策略是大规模多目标优化问题经典的降维策略,其优点是可以大幅减少搜索空间大小,缺点是分组效果会影响算法运行效果。由于三维装箱问题的编码方式可以通过对分组效果进行评价,因此三维装箱问题可以通过具有一定规则的分组策略,加快可行解的搜索速度。
三维装箱问题的分组过程:通过自适应扩展的虚拟集装箱体进行初步虚拟装箱,再将虚拟集装箱配载到所装集装箱内的方法,构建新的装载空间,可以使装载过程更能适应所装货物的变化,增强了空间分配的鲁棒性。根据实验所用箱体,设定规则如下:
1)以带强约束条件的拟人装箱算法为基础进行分组。
2)每组以较大货物为基准进行扩展虚拟集装箱体。
3)每组至少装3个货物且虚拟集装箱体总体积在900 dm3~5 000 dm3之间;
4)每个分组后货物占其对应虚拟集装箱总体积90%以上。
货物分组后的虚拟集装箱体被视为新货物添加到待装货物中,分组操作伪代码如下。
输入 未分组货物数据CargoData
初始化 GroupData=Φ, CargNum=0,VVirtualMax=0, GroupItem=1,CargoDataPacking=CargoData, CargoDataPacked=Φ,
if(900
更新未分组货物数据CargoData=CargoData Packing;
else
if (Length(CargoDataPacking)> 0) then
删除已装货物CargoDataPacking= CargoDataPackingi,CargoNum= CargoNum+1;;
else
break;
end if
end if
else

else
break;
end if
end if
else
end if
end while
分组操作示意图如图5所示,6个货物分为一组,即在解空间中将=(1, 1, 1, 2, 1, 3, 3, 1, 5, 4, 1, 7, 5, 1, 9, 6, 1, 11)简化为=(1, 1, 1),实现了较大程度地降维。

图5 分组操作
3.3 装箱算子及启发式进化设计
考虑到进化算法的核心是进化算子,在装箱问题中,部分匹配交叉、循环交叉以及顺序交叉为3种常见交叉方法。通过实验验证可知,部分匹配交叉的结果更好,但往往进化缓慢。组合优化的优化进程与简单函数优化不同,主要在于连续优化可以取较优解进行均值优化,而三维装箱的决策变量与目标函数的关联性较弱,普通交叉算子或二项式交叉变异算子无法满足均值优化等优化方法的基本需求,因此必须设计新型交叉变异算子,使其适应三维装箱优化问题。姿态近似情况如表2所示
表2 姿态近似规则
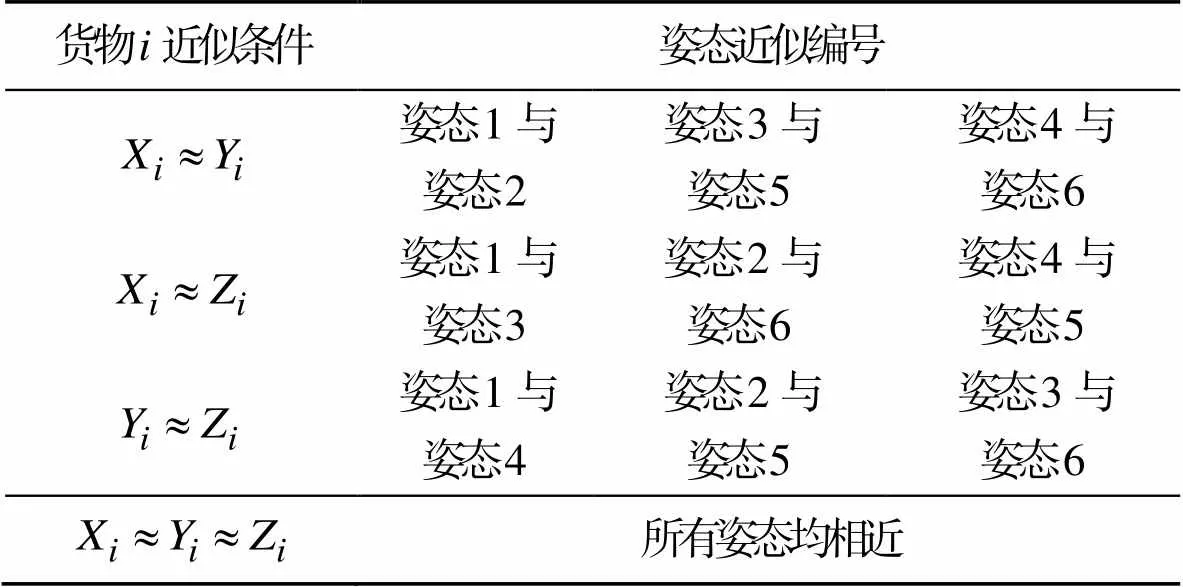
Tab.2 Attitude approximation rule

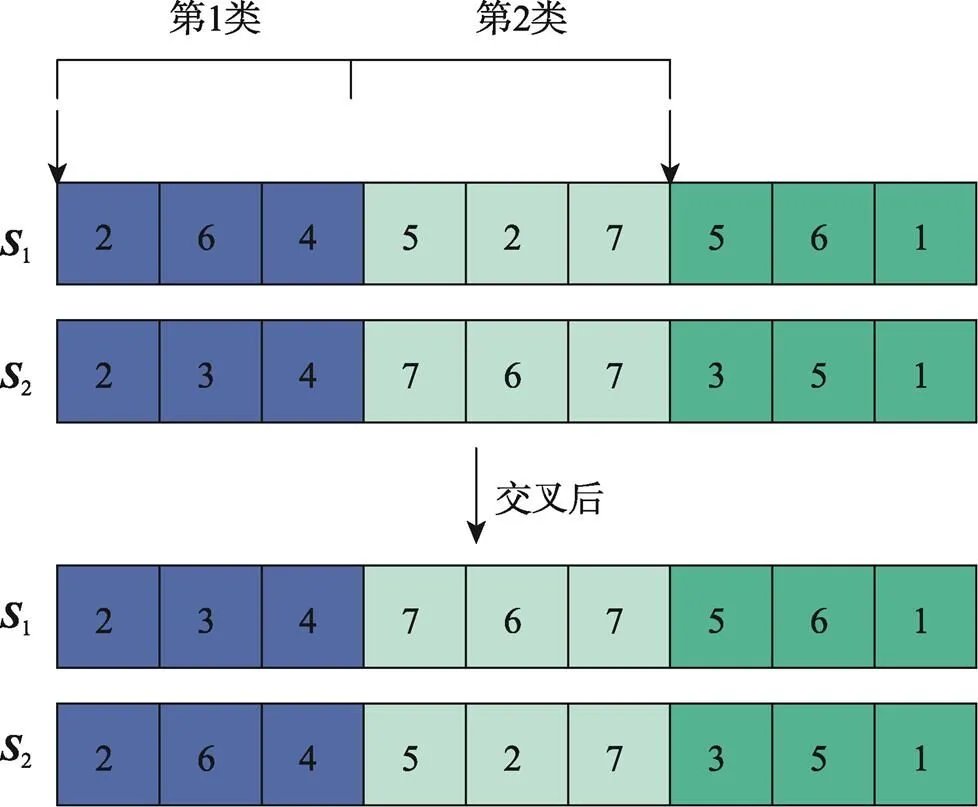
图6 交叉算子
变异操作会加强种群的多样性,采用多种变异策略以避免非成熟收敛情况的出现,同时可以避免因交叉操作引起的局部收敛。随机变异策略,对相似解的少数相同变量进行随机替换,如图7所示。单点变异,选取编码段某随机位置与随机实数进行替换,如图8所示。顺序逆转变异,通过在父代中随机选取2个点作为该变异的变异点,接下来在子代中以与父代中相反的顺序选取2个点进行重新排列,是一种仿生的变异方式,如图9所示。在算法迭代期间,若算法陷入局部最优,即解集某区域附近有较多次优解时使用随机变异策略,探索未知空间,其中次优解指非支配排序中第2序列解。若解集某区域附近有最优解且最优解较少时使用单点变异策略,加快收敛速度,提高收敛程度;顺序逆转变异则在任意解集情况时按变异概率发生。

图7 随机变异策略

图8 单点变异策略
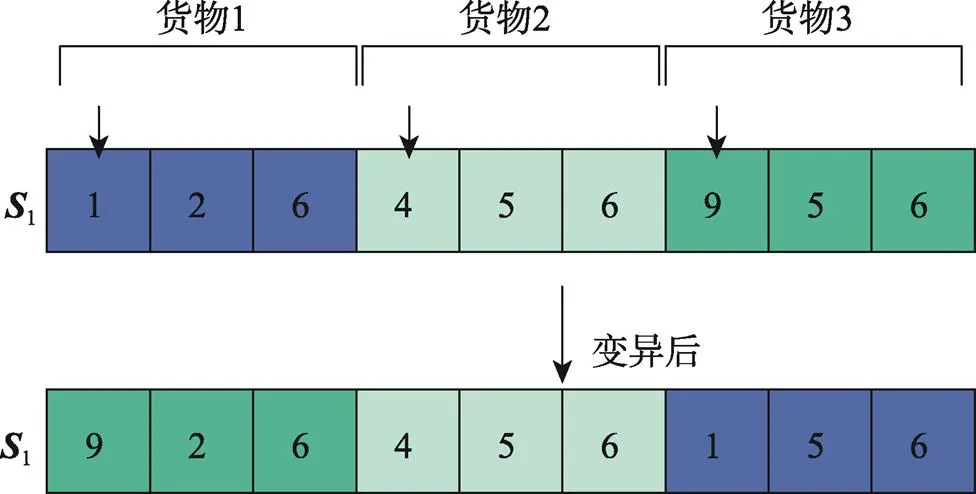
图9 顺序逆转变异策略
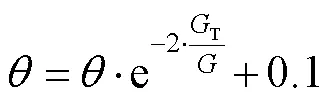
4 结果与分析
为检验文中所提算法的适用性,采用文献[15]中Bischoff & Ratcliff标准算例。算例分为十六大类,BR0~BR7箱型种类为3到20种,是一种弱异构箱型;BR8~BR15箱型种类为30到100种,是一种强异构箱型。BR0~BR15异构性依次增强,每种箱型有若干个待选箱体,进行实验对比的集装箱尺寸为587 cm× 233 cm× 220 cm。为了验证重心位置调整效果,为不同货物设置了不同组的密度,使货物存在一定质量。以BR10算例为例展示部分货物信息,如表3所示,从50组货物中每组抽取2个货物进行分组,分组结果如表4所示。
表3 BR10算例信息

Tab.3 Cargo data of BR10
表4 分组结果

Tab.4 Grouping results
从表5可以得知,用弱异构的BR0~BR7算例进行测试,文献[3]算法所得平均体积利用率为91.125%,码垛的重心位置偏移距离为20.839 6cm,尤其是异构性最弱的BR0、BR2的高度偏移在18 cm以上,有较大安全风险。文献[11]算法所得平均体积利用率为85.880%,码垛重心位置偏移距离为11.240 8 cm;本文所提算法所得平均体积利用率为90.3%,码垛的重心位置偏移距离为3.655 cm。用强异构的BR8~BR15算例进行测试,文献[3]算法所得平均体积利用率为84.175%,码垛的重心位置偏移距离为17.932 5 cm;文献[11]算法所得平均利用率为69.312%,码垛的重心位置偏移距离为12.312 3 cm;本文所提算法所得平均体积利用率为92.0%,平均偏移距离为4.742 5 cm。本文算法在强异构货物的测试时,所得体积利用率与偏移距离均优于文献[3]和文献[11]。
如图10所示,某次装载过程最优解的收敛情况表明,该算法可以在250次迭代时接近近似最优解,求解效率较高。另外,文献[3]算法求解一次耗时51.81 s;本文算法的分组策略降低了90%以上的决策空间,求解一次平均耗时为13.73 s,求解时间比文献[3]降低了73.5%。
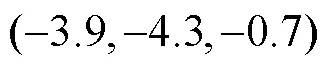
表5 3种算法集装箱体积利用率与重心位置比较
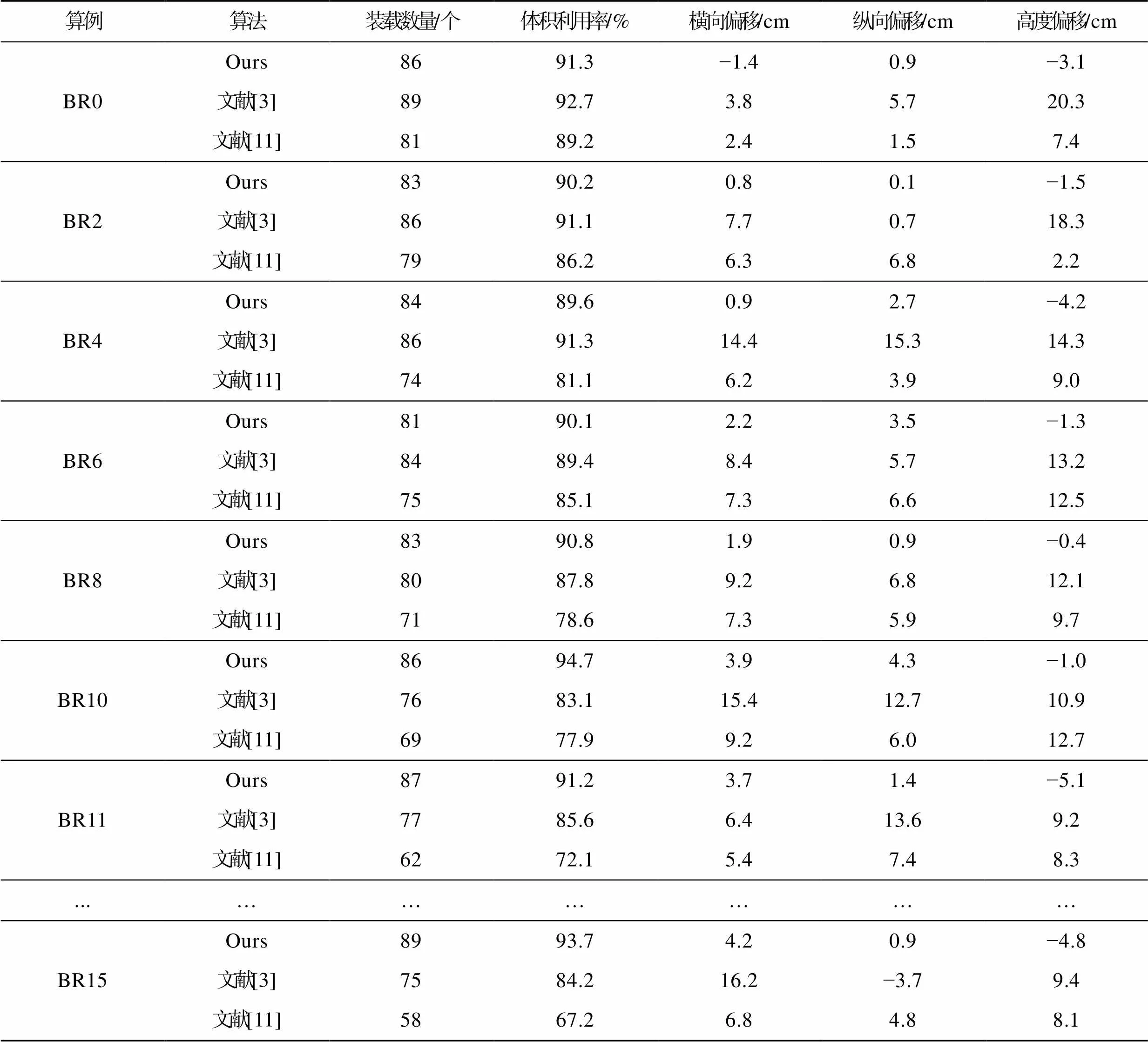
Tab.5 Comparison of container volume utilization rate and center of gravity position
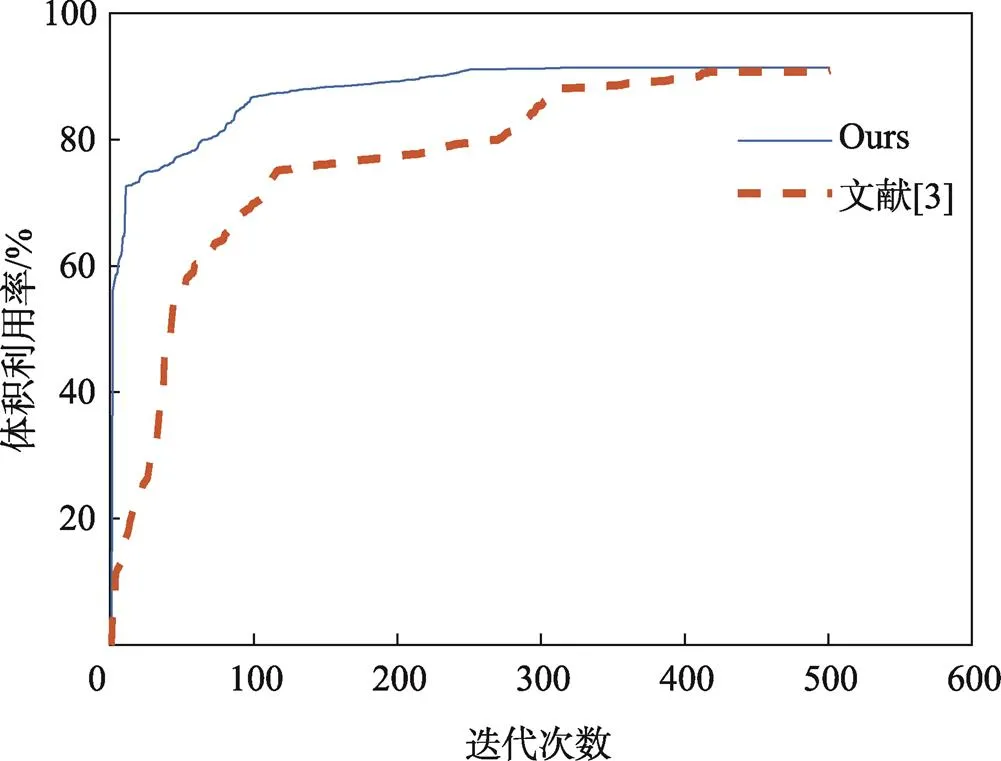
图10 算法性能对比
表6 航空货物装载结果

Tab.6 Air cargo loading results

图11 较优装载规划可视化
5 结语
针对现有的多目标三维装箱算法在求解强异构货物装载问题时寻优能力弱的问题,提出了一种基于分组策略的多目标三维装箱算法。算法以体积利用率和重心位置坐标作为优化目标,通过货物预分组策略和稳定性移位设计降低问题难度,设计自适应选择的装箱进化算子加快收敛,通过标准算例和真实航空货物数据进行实验对比。实验结果表明,该算法可以得到重心位置靠近箱体几何中心的多种装载规划,在求解强异构货物时,算法的装载规划结果明显优于对比算法。将分组策略用于多目标三维装箱优化问题,极大地加快了该问题的求解速度。本文分组规则仍然较为简单,制定更加合理的货物分组规则或设计新型降维策略,是将来多目标装箱问题的重要研究工作。
[1] 张长勇, 翟一鸣. 面向不规则集装箱的货物装载优化问题研究[J]. 计算机应用与软件, 2022, 39(11): 238-244.
ZHANG Chang-yong, ZHAI Yi-ming. Optimization of Cargo Loading for Irregular Containers[J]. Computer Applications and Software, 2022, 39(11): 238-244.
[2] JUNQUEIRA L, MORABITO R, YAMASHITA D. Three-Dimensional Container Loading Models with Cargo Stability and Load Bearing Constraints[J]. Computers & Operations Research, 2012, 39(1): 74-85.
[3] 朱贺. 考虑重心位置的飞机装载优化问题的研究[D]. 北京: 北京交通大学, 2018.
ZHU He. Research on Aircraft Loading Optimization Considering the Position of Center of Gravity[D]. Beijing: Beijing Jiaotong University, 2018.
[4] CHEN Shu-hao, SU Ya-ru, YE Yan-ming, et al. A Hybrid Chemical Reaction Optimization Algorithm for Solving 3D Packing Problem[J]. International Journal of Autonomous and Adaptive Communications Systems, 2021, 14(1/2): 117-131.
[5] Luo Q, Rao Y, Peng D. GA and GWO algorithm for the special bin packing problem encountered in field of aircraft arrangement[J]. Applied Soft Computing, 2022, 114: 108060.
[6] FU Yu, BANERJEE A. Heuristic/Meta-Heuristic Methods for Restricted Bin Packing Problem[J]. Journal of Heuristics, 2020, 26(1): 637-662.
[7] BORGULYA I. A Hybrid Evolutionary Algorithm for the Offline Bin Packing Problem[J]. Central European Journal of Operations Research, 2021, 29(2): 425-445.
[8] HE Kun, TOLE K, NI Fei, et al. Adaptive Large Neighborhood Search for Solving the Circle Bin Packing Problem[J]. Computers & Operations Research, 2021, 127(5): 105140.
[9] 张长勇, 翟一鸣. 基于改进遗传算法的航空集装箱装载问题研究[J]. 北京航空航天大学学报, 2021, 47(7): 1345-1352.
ZHANG Chang-yong, ZHAI Yi-ming. Air Container Loading Based on Improved Genetic Algorithm[J]. Journal of Beijing University of Aeronautics and Astronautics, 2021, 47(7): 1345-1352.
[10] TRIVELLA A, PISINGER D. The Load-Balanced Multi-Dimensional Bin-Packing Problem[J]. Computers and Operations Research, 2016, 74: 152-164.
[11] ERBAYRAK S, ÖZKIR V, YILDIRIM U. Multi-Objective 3D Bin Packing Problem with Load Balance and Product Family Concerns[J]. Computers & Industrial Engineering, 2021, 159(19): 107518.
[12] 赵向领, 李云飞, 李鹏飞. 基于改进遗传算法的航空器载重平衡[J]. 科学技术与工程, 2022, 22(33): 14951-14958.
ZHAO Xiang-ling, LI Yun-fei, LI Peng-fei. Aircraft Load Balance Based on Improved Genetic Algorithm[J]. Science Technology and Engineering, 2022, 22(33): 14951-14958.
[13] 巩梨, 王文璨, 刘林忠. 多目标一维装箱问题模型算法研究[J]. 计算机应用研究, 2020, 37(S2): 144-146.
GONG Li, WANG Wen-jie, LIU Lin-zhong. Research on Model Algorithm of Multi-Objective One-Dimensional Packing Problem[J]. Application Research of Computers, 2020, 37(S2): 144-146.
[14] 侯莹, 吴毅琳, 白星, 等. 数据驱动选择策略的多目标差分进化算法[J]. 控制与决策, 2022, 38(7): 1-9.
HOU Ying, WU Yi-lin, BAI Xing, et al. Multi-Objective Differential Evolution Algorithm with Data-Driven Selection Strategy[J]. Control and Decision, 2022, 39(7): 1-9.
[15] TAKAGI T, TAKADAMA K, SATO H. Weight Vector Arrange1ment Using Virtual Objective Vectors in Decomposition-Based MOEA[C]// 2021 IEEE Congress on Evolutionary Computation (CEC), IEEE, 2021: 1462-1469.
Multi-objective 3D Packing Algorithm Based on Grouping Strategy
ZHANG Chang-yong, WU Gang-xin
(School of Electronic Information and Automation, Civil Aviation University of China, Tianjin 300300, China)
The work aims to propose a multi-objective packing algorithm suitable for large-scale cargo loading to solve the problems of single optimization objective and low optimization efficiency of existing 3D packing algorithms, so as to improve the efficiency of packing planning and ensure the safety of cargo transportation. Firstly, considering five realistic constraints, a multi-objective cargo loading optimization model was established with the volume utilization and the shift of the center of gravity of the loading layout as the optimization objectives. Then, the cargoes were pre-grouped by anthropomorphic packing to reduce the decision space, and the initial solutions were generated by combining the grouping information with the packing algorithm; A data-driven cross operator was introduced to packing to improve the convergence of the algorithm; Multi-strategy mutation operators were designed to improve the diversity of algorithm results. With the public data set and real air cargo data as the experimental data, the experimental results showed that the average volume utilization rate of strongly heterogeneous cargoes in container loading reached 92.0%. The space offset of the center of gravity position was reduced from 20 cm to 7.5 cm. And the running time of the algorithm was reduced by 73.5% under various constraints. Therefore, the algorithm proposed in this paper is applied to solve the large-scale multi-objective three-dimensional packing problem, which improves the packing quality and efficiency, and can provide reference for the engineering application of the three-dimensional packing algorithm.
three-dimensional packing; multi-objective optimization; combinatorial optimization; multiple mutation strategy
TP301;TP311
A
1001-3563(2023)21-0204-10
10.19554/j.cnki.1001-3563.2023.21.025
2023-02-07
民航首台(套)重点项目(3122023PY04)
责任编辑:曾钰婵
