一类弧长与弦长成比例的曲线的构造
2023-11-17明万元黄香蕉杨海波
明万元, 黄香蕉, 杨海波
(南昌航空大学 数学与信息科学学院, 南昌 330063)
0 引 言
对实际问题中具有某种特殊性质的曲线的研究,往往能促进数学的发展. 如,起源于著名油画《蒙娜丽莎》的“悬链线问题”,大大促进了常微分方程的迅速发展[1];1630年意大利科学家伽利略提出的“最速降线问题”,直接导致了变分学的诞生[2-3].
在上世纪九十年代中期,剑桥大学的Hans-Henrik Stφlum教授发现那些发展漫长、路线曲折的古老河流的弯度(即河流长度与其直线距离的比值)通常约为π[4]. 本文不探讨该现象的具体原因,而是考虑一个相关的数学问题:是否存在一条可求长的理想曲线,该条曲线上任一点到曲线起点的弧长与连接这两点的弦长的比值均为π? 下面就该曲线的存在唯一性及其满足的方程进行探讨,并将该问题作进一步推广.
1 平面直角坐标系下曲线的构造
为叙述方便,称平面曲线L具有性质(H),如果L满足以下两个条件:
(i)L的方程y=y(x)∈C1(),起点为O(0,0);

下面在直角坐标系下推导曲线L的方程. 根据性质(H),函数y(x)应满足
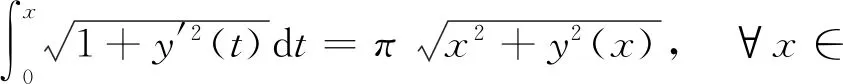
(1)
两边对x求导,得
(2)
将上式整理并改写为
(y-xy′)2=(π2-1)(x+yy′)2.

y-xy′=a(x+yy′).

(3)
其中C1为任意常数. 由隐函数存在定理[5],(3)式在2{(0,0)}内可唯一确定隐式解y=y(x).
在方程(1)中令x=0可得初始条件y(0)=0.但无论(3)式中任意常数C1取何值,点O(0,0)均不在解集(3)中,故原积分方程(1)没有满足初始条件y(0)=0的特解. 也就是说,不存在严格具有性质(H)的曲线.
事实上,由于曲线L的方程y=y(x)∈C1(),故L上任一点处的切线都存在.若取曲线L上与起点O充分靠近的点B,则曲线弧与弦的长度之比应接近于1,而不是π.因此,对任意光滑曲线L,至少在与起点O充分靠近的邻域内,不可能严格满足性质(H).

为构造在上述弱条件下具有该性质的曲线,对微分方程(2)两端同时从0到x积分,可得与(2)同解的积分方程为
(4)


图1 平面直角坐标系下曲线L的示意图
注1y(0)的值可在方程(3)中令x→0+,方程两边同时取极限求得,即
上述所构造的曲线L2的方程(3)比较复杂,较难看出其具体形状,也不便分析该曲线的几何性质. 为更直观地看出该曲线所属的类型,下面再从极坐标系下研究该曲线的方程.
2 极坐标系下曲线的构造

(5)
两边对θ求导,得
(6)
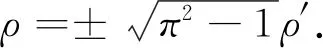
ρ=C2ebθ,
(7)
其中C2为任意非负常数.
由(5)式得初始条件ρ(0)=0,将其代入(7)式得C2=0,从而ρ≡0.故方程(5)没有非平凡解.
类似地,为构造弱条件下弧长与弦长成比例的曲线,将微分方程(6)两端同时从0到θ积分,即得与(6)同解的积分方程为


图2 极坐标系下曲线L的示意图
注2 曲线L=L1+L2的真实图形如图3所示,其中L2的方程为ρ=C2ebθ,其表示的正是对数螺旋线[6]. 当b>0时,该螺旋线向外旋转至无穷;当b<0时,该螺旋线向内旋转并趋于极点. 自然界中对数螺旋线非常普遍,如蜗牛壳、蜘蛛网以及银河系的旋臂等[7-9].

图3 极坐标系下曲线L的图形
注3 利用直角坐标与极坐标之间的变换公式,容易验证方程(3)与方程(7)表示的是同一条曲线.
3 推 广
上节中曲线的构造与推导方法可推广至更一般的弧长与弦长成k(k>1)倍的情形.

进一步地,还可将具有该性质的平面曲线推广至空间曲线的情形.
命题2设空间曲线Γ的起点为O(0,0,0),Γ由两段光滑曲线Γ1与Γ2拼接而成,其连接点为A.若Γ2的方程由
(8)

注4 易见,若在方程(8)中取t=0,k=π,则退化为平面曲线(3).
4 结 论
本文从实际问题中河流长度与其直线距离的比值关系出发,构造了一类在特定条件下(即从曲线上某点之后开始)曲线上任一点与曲线起点之间的弧长与弦长成比例的曲线. 结论表明:若不考虑该曲线初始弧段(即文中的曲线L1)的形状,则该平面曲线的类型是唯一确定的,即对数螺旋线.
本文的结论在一定程度上丰富了对数螺旋线的优美性质,所采用的方法对构造具有某些特殊性质的曲线也有一定的启示. 当然,本文仅考虑了分段光滑的曲线,对更一般的曲线(如,分形)未作探讨.
致谢作者非常感谢相关文献对本文的启发以及审稿专家提出的宝贵意见.
