球面坐标系中三重积分体积微元的分析
2023-11-17杨怀君周永卫
杨怀君, 周永卫, 刘 林
(郑州航空工业管理学院 数学学院,郑州 450046)
0 引 言
三重积分是高等数学教学中的一个重点和难点,特别是球面坐标系下的三重积分的计算,球坐标系在地理学、天文学中有着广泛应用.球面坐标系下计算三重积分的一个关键点是讲解清楚该坐标系下的体积微元公式.熟练掌握三重积分特别是球面坐标系下三重积分的计算是高等数学教学中的一个重要目标[1-3],对学生空间想象能力的培养和逻辑思维能力的训练都有很大的帮助.文献[4-5]从Jacobi变换的角度给出球面坐标系下三重积分的体积微元公式,从而给出球面坐标系下的三重积分的计算方法,这种方式严谨但比较抽象.现有的高等数学类教材都是从近似的角度出发[6],将体积的增量在不计高阶无穷小的情况下将这个六面体看成长方体给出球面坐标系下的体积微元公式.该方式尽管直观但似乎又缺少一些严谨.结合近几年的教学实践,从体积增量的角度出发,给出一种既具体直观而又不缺失严谨的方式来给出球面坐标系下三重积分的体积微元公式的研究成果还不多见.尽管在文献[7]中给出了球面坐标系中三重积分的体积元素的无穷小分析,但分析过程较为抽象,不易于学生的理解,本文以一种不仅具体直观易于学生理解而又不缺失严谨的理论分析的方式给出球面坐标系中三重积分的体积元素的无穷小分析,这里所谓的具体直观是通过MATLAB[8]绘图让体积增量直观具体且形象,所谓的不失严谨是给出不计高阶无穷小的理论分析.本文的结果将为球面坐标系下的三重积分这个教学重点和难点提供一种简单易教的教学思路和方式,具有一定的参考价值.
1 坐标变换的方式
球面坐标是以坐标原点为参考点,由方位角θ、仰角φ和距离r构成[4-6].这里,参数r,φ,θ的取值范围为
从图1中可以看出,当r,φ,θ分别取常数时,其表示如下的特殊曲面,即r=常数表示以原点为球心的球面,φ=常数表示以原点为顶点且与z轴的夹角为φ的圆锥面,θ=常数表示过z轴的半平面.从图1中不难看出,球面坐标系(r,φ,θ)与直角坐标系(x,y,z)之间有如下的变换关系:

图1 球面坐标系示意图
从而,从球面坐标系到直角坐标系的Jacobi变换矩阵为
Jacobi变换矩阵的行列式为
|J(r,φ,θ)|=cosφ(r2sinφcosφcos2θ+r2sinφcosφsin2θ)
+rsinφ(rsin2φcos2θ+rsin2φsin2θ)
=r2sinφcos2φ+r2sinφsin2φ=r2sinφ.
那么,在球面坐标系下的体积微元公式[4-5]为
dV=dxdydz=r2sinφdrdφdθ.
(1)
2 体积增量的方式
上述方式从严谨的理论分析层面给出了球面坐标系下的体积微元公式,但这种方式在高等数学的教学中学生并不容易理解,尽管上述过程简洁,但不是很直观.下面将从体积增量的角度,并结合具体图形,形象直观地来给出球面坐标系下的体积微元公式 (1).


图2 距离为r仰角为φ所围的区域
由三重积分的几何意义和柱面坐标系的计算方法可以得出此闭区域Ω的体积为
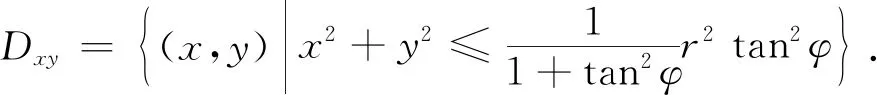
先看当距离r不变,仰角φ变化到φ+dφ,方位角θ的变化范围为[0,2π]时,这时的体积改变量如图3中的阴影部分.
从前面的推导过程,可以得出阴影部分的体积为

现在让距离r变化到r+dr,方位角θ的变化范围为[0,2π].此时当仰角φ变化到φ+dφ时,又有一个类似于图3中阴影部分的体积,这时的体积为
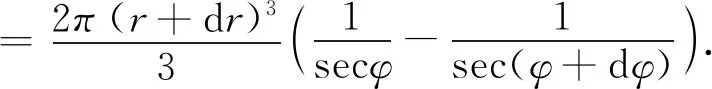
那么,当距离r→r+dr,仰角φ→φ+dφ,方向角θ∈[0,2π]时,体积的改变量如图4中的除去网格线的阴影部分所示,这部分的体积记为V增,则有

图4 距离为r→r+dr仰角为φ→φ+dφ所围区域
V增=[V(r+dr,φ+dφ)-V(r+dr,φ)]
-[V(r,φ+dφ)-V(r,φ)]
此时再考虑方位角θ→θ+dθ,如图5深色阴影部分所示,这时的体积增量记为ΔV,这个体积的增量ΔV可看成垂直于xoy的平面截图4深色阴影部分所得截面绕z轴旋转了一个dθ的角度生成,而V增可看成截面绕z轴旋转了一个2π的角度生成,根据角度的比例关系来确定切割[7],即
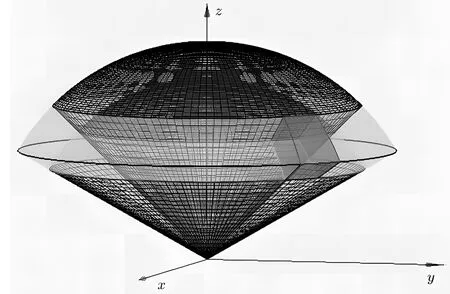
图5 体积增量ΔV的示意图
那么,可以得出
由和差化积公式,上式可化简为
若记
接下来,需要证明α(dr,dφ,dθ)是dr→0,dφ→0,dθ→0时的高阶无穷小[7].为此,记
α(dr,dφ,dθ)=α1(dr,dφ,dθ)+α2(dr,dφ,dθ)+α3(dr,dφ,dθ),
其中



从而可以得出
综上,得到
因此,ΔV=r2sinφdrdφdθ+o(drdφdθ),进而如文献[6]中所述,将这个增加的空间区域近似看为长方体是合理的,其体积微元公式为dV=r2sinφdrdφdθ.
3 结 论
文中以一种既直观而又不失严谨的方式给出球面坐标系下三重积分的体积微元公式,一方面可以帮助学生更为深刻地理解球面坐标系下的三重积分的计算,另一方面可以激发学生们的学习兴趣和动手实践能力,通过动手进行MATLAB绘图加深对球面坐标系下三重积分体积微元公式的理解.
致谢作者非常感谢相关文献对本文的启发以及审稿专家提出的宝贵意见.
