新型吊杆布置系杆拱桥结构受力分析

郝佳佳

[同济大学建筑设计研究院（集团）有限公司，上海市 200092]

0 引言

21 世纪以来，中国钢拱桥的建设技术飞速发展，建造数量迅速增加，而且已建拱桥多采用跨度200 m 以内的中下承式无铰拱结构[1]。城市桥梁与人民生活紧密联系，随着生活水平的不断改善，人们对桥梁景观的要求显著提高，而中承式系杆拱桥不仅能融和大部分的城市环境，而且有丰富多样的景观，理所当然地成为了城市桥梁设计中常用的桥梁形式。

城市桥梁的景观设计往往是针对不同结构构件的造型设计，景观拱桥通过对拱肋、主梁、吊杆、拱间横撑等构件的特殊设计（形状与布置）营造特有的桥梁效果。目前，单拱肋、拱肋内倾提篮拱、拱肋外倾蝴蝶拱等是常见的景观拱桥设计造型，随着建筑材料、建造工艺、施工方法地不断改进提升，异形拱肋构造、新型吊杆布置拱桥等得以施建，达到了独树一帜的桥梁景观效果。本文研究了新型吊杆布置拱桥结构设计、关键参数和工程实例，为城市桥梁的景观设计增添新思路，也进一步丰富了拱桥形式。

1 扇形吊杆系杆拱桥总体设计

1.1 吊杆布置形式

拱桥的景观设计应更注重总体布置，虽然不可否认桥梁细节设计对整体景观的改善，但吊杆布置形式、矢跨比、拱轴线线形等总体参数对拱桥景观效果的影响更为直观。

系杆拱的吊杆布置形式主要有竖直吊杆、倾斜吊杆、网状吊杆、单向倾斜吊杆[2]、扇形吊杆、空间索网等以及各形式的组合布置，如图1 各图所示。

图1 系杆拱的吊杆布置形式

与竖直吊杆系杆拱相比，扇形吊杆布置系杆拱的设计参数关键在于吊杆圆心角α，其反映了吊杆布置聚集程度，是扇形吊杆布置系杆拱区别于其他拱桥形式的特征参数。吊杆圆心角α 既影响着桥梁总体景观，也是本文的重点研究对象。扇形吊杆布置拱桥的基本思路如图2 所示。

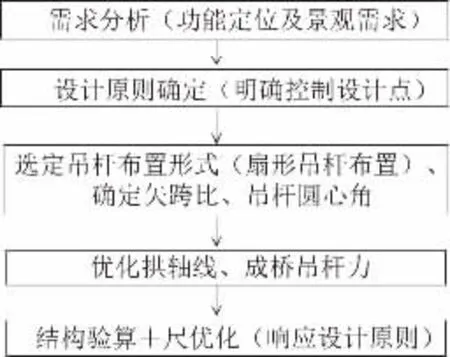
图2 扇形吊杆布置拱桥的设计思路

1.2 矢跨比

矢跨比对拱的内力有重要影响，实际工程的矢跨比通常在1/3 至1/12 之间，又以1/4～1/6 最多。

扇形吊杆布置拱桥的矢跨比可取大值，既能显得桥拱高耸挺拔，景观效果更好，又有利于扇形吊杆的展开布置，建议取值为1/4～1/5 之间。

1.3 合理拱轴线

合理拱轴线是相对合理的概念，实际工程的荷载条件难以确定，更关注找到满足工程要求的拱轴线。随着钢结构的广泛运用，拱肋对拱轴线的合理程度有了更高的偏差容忍度。

常用的拱轴线数学模型有圆弧线、抛物线、悬链线和样条曲线等几种，从操作实用程度和受力合理性两个方面考虑，又以悬链线和二次抛物线居多，而钢结构拱更适合二次抛物线。

扇形吊杆布置拱桥的合理拱轴线较为特殊，应根据有无吊杆分区段设计，有吊杆区拱轴线采用抛物线，无吊杆区用圆弧线接顺。

2 扇形吊杆布置系杆拱关键参数分析

2.1 桥例参数及分析思路

为分析不同吊杆圆心角α 的系杆拱结构受力特征，以桥跨100 m、桥宽35 m、矢高25 m、吊杆梁上锚点间距6 m、两片拱设置4 道风撑、拱间距25 m 的系杆拱为例，取活载作用下影响线所围面积（计为Ayxx）作为比较依据，以判断扇形吊杆布置拱结构的力学性能。

拱梁刚度比（EI）拱/（EI）梁=1，属于刚性梁刚性拱结构[3]。

2.2 内力影响线分析

2.2.1 拱肋内力影响线分析

如图3 至图5 所示，影响线分析表明，当α 小于40°时，拱肋内力影响线变化较小。竖直吊杆（α=0°）拱肋轴力影响线呈对称形态；而扇形吊杆布置拱肋轴力逐渐呈现出偏态性；以α=0°为比较基准，随着α的增大，拱肋四分点弯矩和拱脚轴力的影响线面积Ayxx 逐渐减小，而拱顶、拱脚弯矩影响线面积Ayxx逐渐增大，α=80°时拱肋弯矩影响线面积Ayxx 趋于相同。

图3 对应各α 拱肋轴力影响线（单位：m）

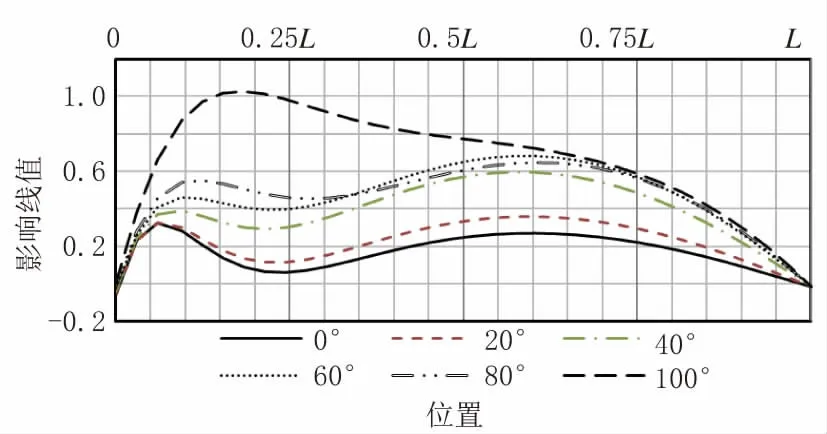
图4 对应各α 拱脚弯矩影响线（单位：m）

图5 拱内力影响线Ayxx 随α 增大的关系（单位：m）

2.2.2 系梁内力影响线分析

如图6 至图8 所示，参数α 的变化基本不影响系梁内力影响线的形态，但当α≥100°时系梁内力的受影响范围明显缩小。随着α 增大，系梁轴力Ayxx没有明显差异，而梁四分点、跨中弯矩Ayxx 逐渐减小，且四分点处弯矩降低明显。由此可知，扇形吊杆布置将有效改善系梁四分点处受力。

图6 对应各α 梁轴力影响线（单位：m）

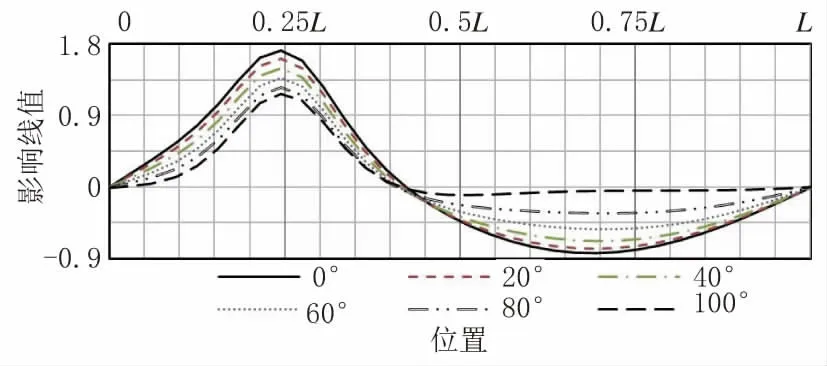
图7 对应各α 梁四分点弯矩影响线（单位：m）

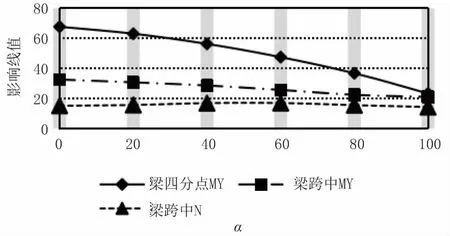
图8 系梁内力影响线Ayxx 与参数α 的关系（单位：m）

2.2.3 吊杆轴力影响线分析

如图9 至图10 所示竖直吊杆（α=0°）在汽车作用下均为受拉状态，中吊杆轴力影响线是对称形态的，随着α 增大，中吊杆轴力影响线在靠近拱脚处局部出现压力。

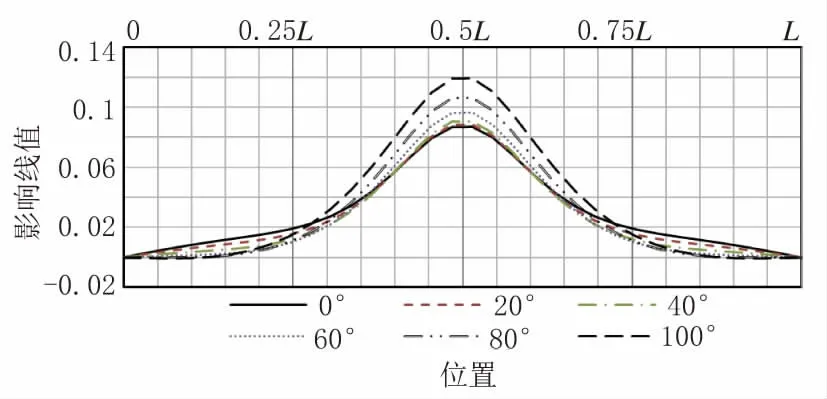
图9 对应各α 中吊杆力影响线（单位：m）

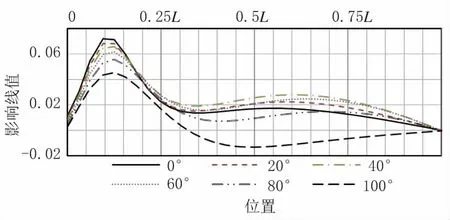
图10 对应各α 边吊杆力影响线（单位：m）

边吊杆轴力影响线是非对称的，呈现出两个波峰的形态，边吊杆轴力影响线随α 增大趋于均匀。

如图11 所示，当α≥100°时，边吊杆出现较大范围压力区，且区段覆盖了远离边吊杆的整个3/4 跨。从吊杆疲劳效应看，由于钢结构系杆拱桥的活载占比较大，对于α≥100°的扇形吊杆布置系杆拱，其边吊杆疲劳应力幅应引起足够重视。

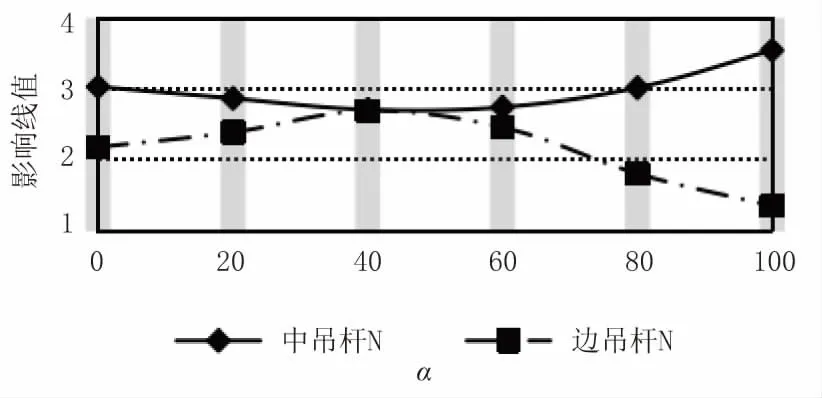
图11 吊杆轴力影响线Ayxx 与参数α 的关系

中吊杆轴力影响线虽有受压段，但影响线受拉面积仍比受压面积大很多，且由于拉压抵消，中吊杆轴力影响线Ayxx 在α=45°最小。

从吊杆受力均匀的角度考虑，α=40°的边、中吊杆轴力影响线Ayxx 基本一致。

2.3 挠度影响线分析

如图12 至图13 所示，拱梁跨中挠度的影响线有正有负，且随着α 增加，影响线的正面积逐渐减小，当α＞40°时扇形吊杆布置拱桥的反向影响线消失，这也导致结构竖向刚度随着α 增加而逐渐降低，而55°＜α＜85°的结构竖向刚度变化较小。

图12 各α 的梁跨中挠度影响线（单位：mm）

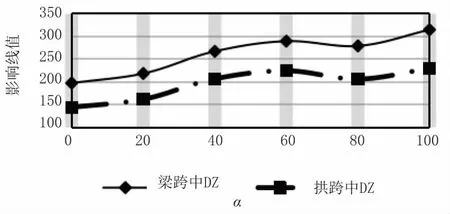
图13 拱梁跨中挠度影响线Ayxx 与参数α 的关系（单位：mm）

2.4 动力特征分析

作为重要的结构动力特征，自振频率是本次分析的重点。基于竖直吊杆、扇形吊杆布置拱桥的空间结构模态分析，前5 阶振型主要有6 种形态，频率及振型形状详见表1。

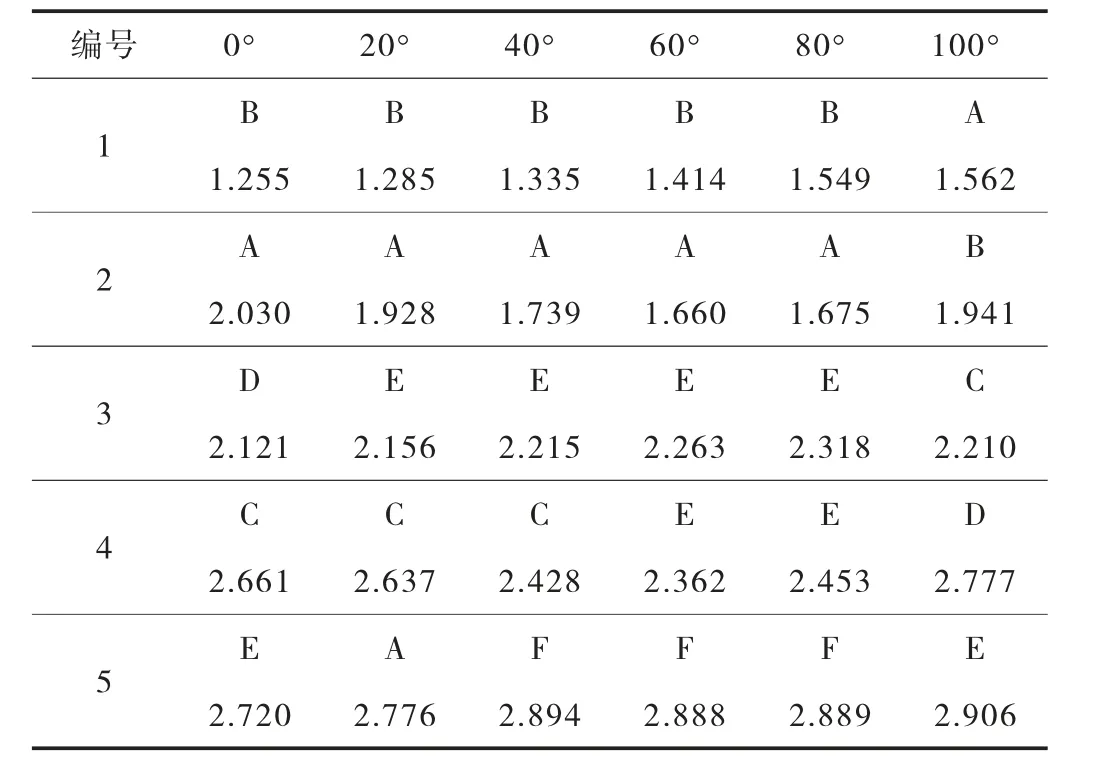
表1 各α 前5 阶典型振型自振频率汇总表 单位：Hz

由动力特征分析结果可知，竖平面内系杆拱结构弯曲振动的一阶频率受吊杆布置聚集程度的影响较大，且随着α 增加而逐渐增大；而侧向自振频率与吊杆布置聚集程度的关系不大，最低阶的频率值基本为2.2 Hz。

吊杆的扇形集聚布置，能有效提高结构一阶频率，这将成为一项改善结构动力性能的有力措施。

2.5 效益分析

相比梁桥结构，系杆拱的系梁由于存在吊杆支撑效应，使得系梁弯矩极大改善。为比较系杆拱的结构效益，通过计算系杆拱效应引起的弯矩减小程度，引入系梁弯矩卸荷比η 的概念，η=1-（系杆拱弯矩影响线正面积/ 对应简支梁弯矩影响线面积），将各α取值下的η 值列于表2。

表2 各α 系梁弯矩卸荷比η 汇总表 单位：%

由表可知，η 值受α 的影响较小，均在95%左右，且当α=40°时η 最小，为提高结构效益，α 应尽量避开40°取值。

3 工程实例分析

3.1 工程概况及总体设计

某工程是一市区跨河桥梁工程，由主桥+引桥组成，主桥采用钢结构系杆拱结构，以97 m 跨径跨越景观河道，桥宽31.5 m，在两榀拱中间布置20 m宽车行道，在系梁外侧悬挑布置3.25 m 宽人行道。

桥位临近城市公园，有较高的景观需求。本桥的设计重点在于拱肋，应尽量控制拱肋尺寸，以保证景观效果。本桥计算跨径92.84 m，矢跨比取1/4，拱矢高23.21 m。为提升桥梁景观，采用扇形吊杆布置，综合比选各吊杆圆心角下结构性能后可知，当取α=60°时，拱梁内力分配合理，拱肋尺寸满足景观需求，吊杆受力更均匀。图14 为计算模型图。

图14 计算模型图

3.2 关键构造设计

扇形布置使得吊杆拱上锚固点集聚，这是景观特色，也是设计关键点。集中锚固增加了锚固构造的设计难度，且吊杆倾斜导致了其与拱肋间夹角减小，设计时也应特别注意，同时斜吊杆具有类似于斜拉桥拉索的受力模式。

实际工程应结合具体的锚固形式确定合理的布置间距。以该工程为例，基本组合下吊杆力约为255 t，拱上吊杆锚固采用耳板形式，为尽量利用常规系杆拱构造，本工程锚固间距控制在6 m 左右。

4 结论

扇形吊杆布置作为一种新型吊杆布置方式，与传统的直吊杆拱桥相比，更具景观优势，且有其独特的力学特性。分析结果表明：

（1）通过对比分析各种吊杆圆心角α 系杆拱的静、动力性能可知，梁拱轴力及系梁跨中弯矩变化幅度较小，而拱肋弯矩及系梁四分点弯矩变化较大，竖平面内结构弯曲振动的一阶频率随着α 增加而逐渐增大。

（2）对于α≥100°的扇形吊杆布置系杆拱，边吊杆出现压力影响线，其吊杆疲劳效应应引起足够重视。

（3）相比α=0°时的竖直吊杆布置，扇形吊杆布置宜取α=60°，拱梁内力更均匀，吊杆受力较合理，且有效提高结构一阶频率。

（4）吊杆圆心角α 是景观设计的重要参数，反映了吊杆布置聚集程度，也决定了扇形吊杆布置系杆拱构造设计的关键——吊杆锚固，吊杆的集中布置、以及倾斜吊杆与拱肋间夹角减小，都极大地增加了设计难度，实际工程应结合具体的锚固形式，确定合适的吊杆锚固间距。

（5）扇形吊杆布置系杆拱的拱肋稳定性、吊杆风振性能，将是下一步的研究方向。除了通过调整α 来获得扇形吊杆布置的景观效果之外，将扇形吊杆与连拱、偏态拱组合，也将进一步丰富景观拱形式。