基于LM算法的BP神经网络的光伏故障实时在线诊断方法研究

曾瑞江，黄缙华，李志勇

南方电网公司电网自动化重点实验室(广东电网有限责任公司电力科学研究院)，广东广州，510630

0 引言

传统的光伏发电系统故障诊断方法主要分为两类：一类是基于传统的电特性参数或电气特性的故障诊断方法，如电参数法、电气特性法和开路电压法；另一类是基于神经网络的故障诊断方法，如BP神经网络、径向基（RBF）神经网络等。以上两类故障诊断方法均是在光伏发电系统出现故障后才能进行，若在未出现故障时即发现或检测到了故障，则会导致检测结果出现偏差，甚至误报。针对上述问题，本文提出了一种基于LM算法的BP神经网络的光伏组件故障实时在线诊断方法，该方法能够根据实际光伏组件出现的各种故障类型，动态识别光伏组件发生的各种故障。本文所提出的基于LM算法的BP神经网络的光伏组件故障实时在线诊断方法，与传统方法相比，具有较高的识别准确率，且检测时间短、效率高、无需维护[1-3]。

1 预测模型的输入

本文中采用的预测模型来自Simulink仿真软件中的SimPowerSystems模块。Simulink是美国国家可再生能源实验室开发的一种用于模拟与仿真的软件工具，具有强大的仿真功能，可以快速、方便地建立复杂系统的仿真模型。Simulink提供了强大的建模、仿真、分析工具，使用其进行仿真实验具有很大的优势。为了方便对光伏阵列进行故障预测，本文采用Simulink对光伏阵列输出功率进行仿真实验[4-5]。

光伏阵列的输出功率计算公式为：

公式中：P表示光伏阵列的能量转换效率，S表示光伏阵列的容量，l表示太阳光的照射强度，Tc表示温度[6]。

由于辐射强度是影响太阳能电池阵列发电效率的重要因素，我们使用Simulink进行计算，模拟一个由单元×10太阳能光伏发电器件阵列组成的系统。该系统的额定功率为213.15W，故障电流为784A，型号为SSH-215。我们通过这个模拟得到环境温度和辐射强度对输出功率的影响曲线，分别如图1和图2所示。

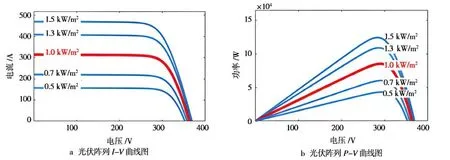
图1 光伏阵列随辐射强度变化曲线图

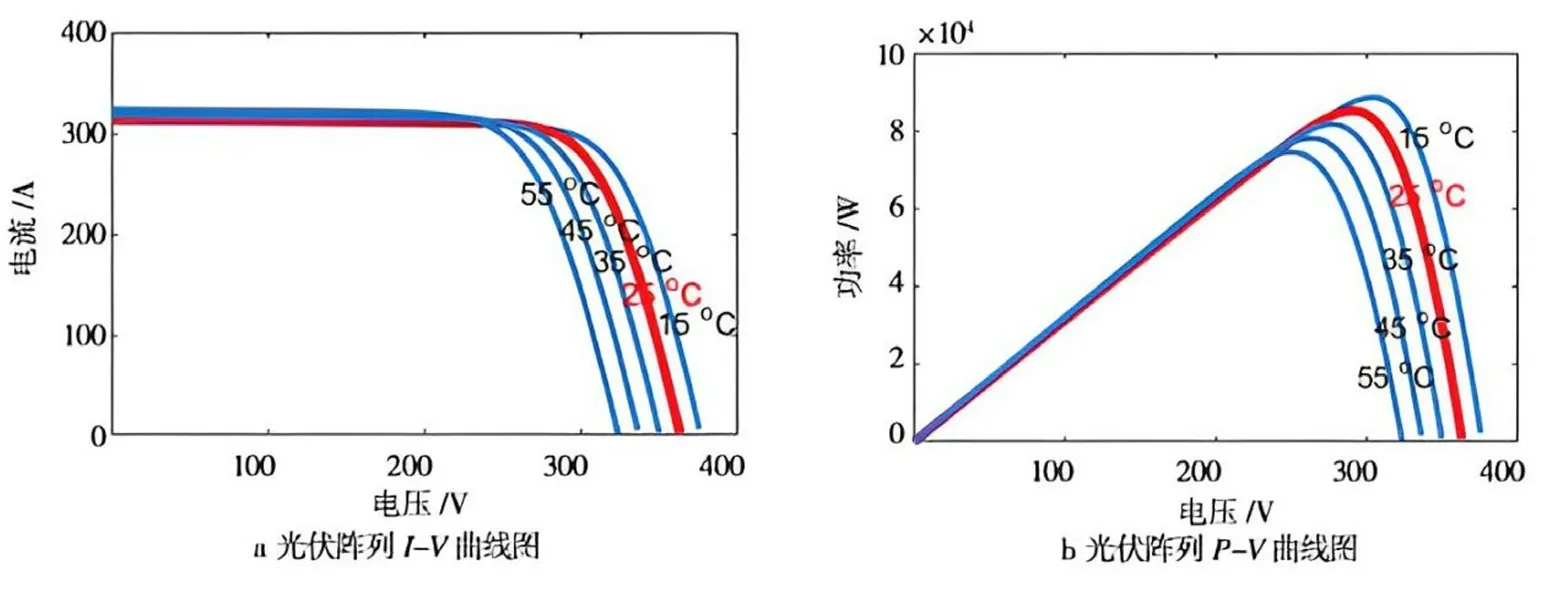
图2 光伏阵列随环境温度变化曲线图

1.1 辐射强度对光伏阵列输出功率的影响

图1的结果显示，在温度为25℃时，我们可以观察到在l-V曲线上，随着流量的增加，出口流量基本保持不变。当流量超过开关压力时，光电阵列的流量会急剧下降。此外，我们还可以观察到随着照射度的增加，流量也随之增加。而在P-V曲线上，每条曲线都有一个峰值点，即输出能量最大的点。此外，照明程度越高，输出能量也越大。因此，我们可以将辐射强度作为BP神经网络模型的一个输入参数。由于外部环境，如季节和气候等，都与太阳辐射相关，所以我们将其纳入辐射范畴进行研究和讨论。

1.2 环境温度对光伏阵列输出功率的影响

在标准辐射（1000W/m2）下，图2展示了光伏阵列在环境温度变化下的l-V和P-V曲线。从图中可以观察到，光伏阵列的电压基本上不受温度的影响。然而，光伏阵列的输入和输出能量会受到周围环境气温变化的限制。当电压超过规定值时，随着周围环境气温的升高，会导致输入输出功率的下降[7]。因此，考虑到环境气温对光伏阵列输入和输出能量的限制，我们选择温度作为BP神经网络模型的输入参数。

1.3 故障程度对光伏阵列输出功率的影响

如图3所示，失效面积愈大，太阳能电池模块的输出就愈小。在此基础上，建立了一种基于BP神经网络的太阳能电池板故障预测模型，并对其进行了实验验证。

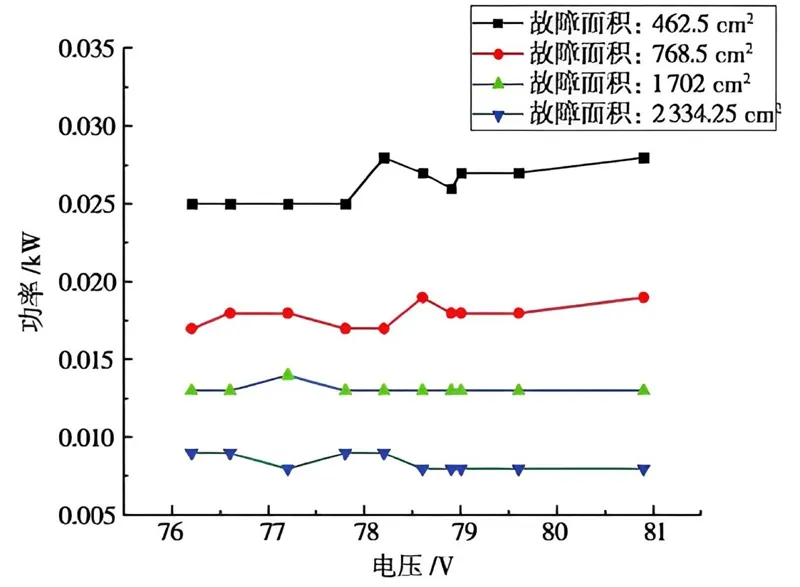
图3 不同故障面积下P-V 曲线图

2 预测模型的建立及改进

本文旨在建立BP神经网络预测模型，用于估算单个故障光伏模块的输入输出能量。通过评估光伏模块的故障程度，我们可以判断该模块是否仍能正常工作。对于具有相同并联模块数量的情况，预测模型的输入/输出能量就是每个故障模块的输入/输出能量。对于具有多块并联模块的情况，模型估算的输入/输出能量是每个并联光伏模块的总输入/输出能量。基于此，我们需要对多个并联模块进行预测，并将预测能量与其他正常模块的能量差相乘，以获得单个故障模块的能量值。具体来说，对于具有相同并联模块数量的情况，每个并联模块都有自己的预测输入/输出能量，该模块的预测输入/输出能量应该等于该模块正常工作时的输入/输出能量。该方法解决了BP神经网络中当网络层数较多时，学习过程较为复杂的问题。本文采用了一种基于LM算法的BP神经网络来构建预测模型，该模型使用了LM算法来确定BP神经网络模型中各个神经元的权值和阈值。LM算法是一种基于梯度下降法的全局优化算法，具有搜索速度快、计算精度高等特点。

2.1 BP神经网络预测模型的建立

BP神经网络结构如图4所示。

本文预测模型中使用了三个输入变量来描述光伏模块的特性：初始状态、模块故障状态和正常工作状态。预测模型的输入变量如表1所示。

表1 预测模型的输入变量

并以此为基础，对各种故障情况下的光伏组件对整体发电性能的影响进行了分析。在此基础上，本文提出了一种新的太阳能电池板的设计方法。隐节点的选择对网络的规模、性能有很大的影响。为增加模型稳定性，本文选用如下公式确定隐藏层节点数。

2.2 激活函数的确定

神经网络需要一个能处理全部输入信息的初值，而初值必须与原点的对称性有关[8]。BP神经网络中常见的激活函数有：sigmoid参数、Relu参数和purelin参数，sigmoid参数又可以被划分为logsig参数和tansig参数，其中tansig参数和purelin参数是与原点对称有关的。为此，我们选取了与原点对称性有关的tansig及purelin两个变量，并将其作为激活函数。BP神经网络预测模型如图5所示。

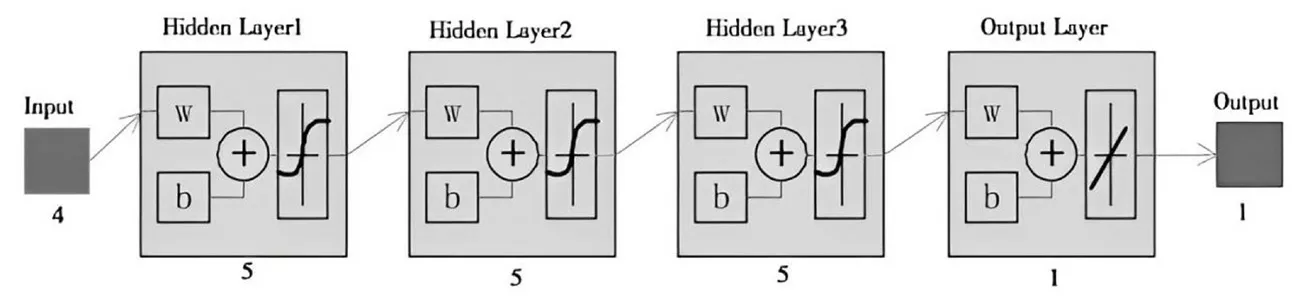
图5 BP 神经网络预测模型

对于每个光伏模块，其输出电压可以由一个电压传感器获得，传感器的输出电压与模块的电流和电压有关。但是在实际应用中，光伏模块并不是固定在光伏电池板上，而是随着时间的推移会发生倾斜和偏移。因此，我们需要建立一个基于时间变量的输出能量预测模型。该模型只需计算当前时刻的输出能量即可。对于具有相同并联模块数量的情况，光伏模块的输出电压可以用一系列预测模型来表示，而每个预测模型都需要计算输入/输出能量、功率损耗和电流损耗等参数。通过将上述计算结果与实际值进行比较，可以得到相应的预测模型并实现其预测功能。

2.3 BP神经网络预测模型的改进

BP神经网络在网络理论和性能方面已经相当成熟，但仍存在一些问题，例如容易陷入局部极小值和收敛速度缓慢等。针对这些问题，通过比较改进的LM和SCG方法的预测模型，并对BP神经网络中的错误进行改进[9]。

LM算法是一种介于牛顿法与梯级法之间的非线性参数改进技术，其迭代公式如下，可以对该算法的误差进行修正，该算法在迭代时始终遵循着负梯度的方向，并将错误按上升的方向进行查找，并通过反复迭代来找出适合的因子u，从而解决网络中存在的下确界问题。

SCG算法主要是对共轭梯度法和量化步长进行了改进，使得量化步长得到了较高的精度，同时还考虑了Hessian矩阵的正态。

3 分析和结果

3.1 评价模式

在电力系统中，有多种方法可用于预测电力系统的表现。常用的评估指标包括均方根偏差（RMSE）、平均绝对误差（MAE）、平均绝对百分比误差（MAPE）以及均方误差（MSE）。通过使用MSE和MAPE进行精度评估，其计算公式如下所示：

3.2 SCG和LM的比较

图6为用SCG算法对预报模型进行了修改，并用LM算法对其进行了校正。LM算法误差变化幅度在±0.02左右，SCG误差范围基本维持在±0.04的范围之内，但误差幅度较大。两种最优解的平均方差衰减曲线示于图7。从图中可以看出，利用SCG算法进行了50次预测，在平均训练时间为44次的情况下，BP神经网络的稳定性要好很多，实际上，它的边际变化是0.0008568。LM算法中的修正后的预测模型经过47次的训练，在平均训练时间为41次的情况下，该模型的稳定性得到了较好的改善，但其真实误差为0.000076367。

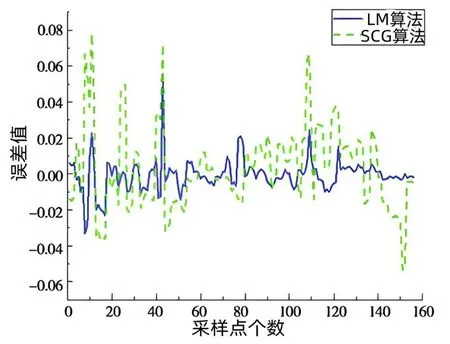
图6 误差分析图

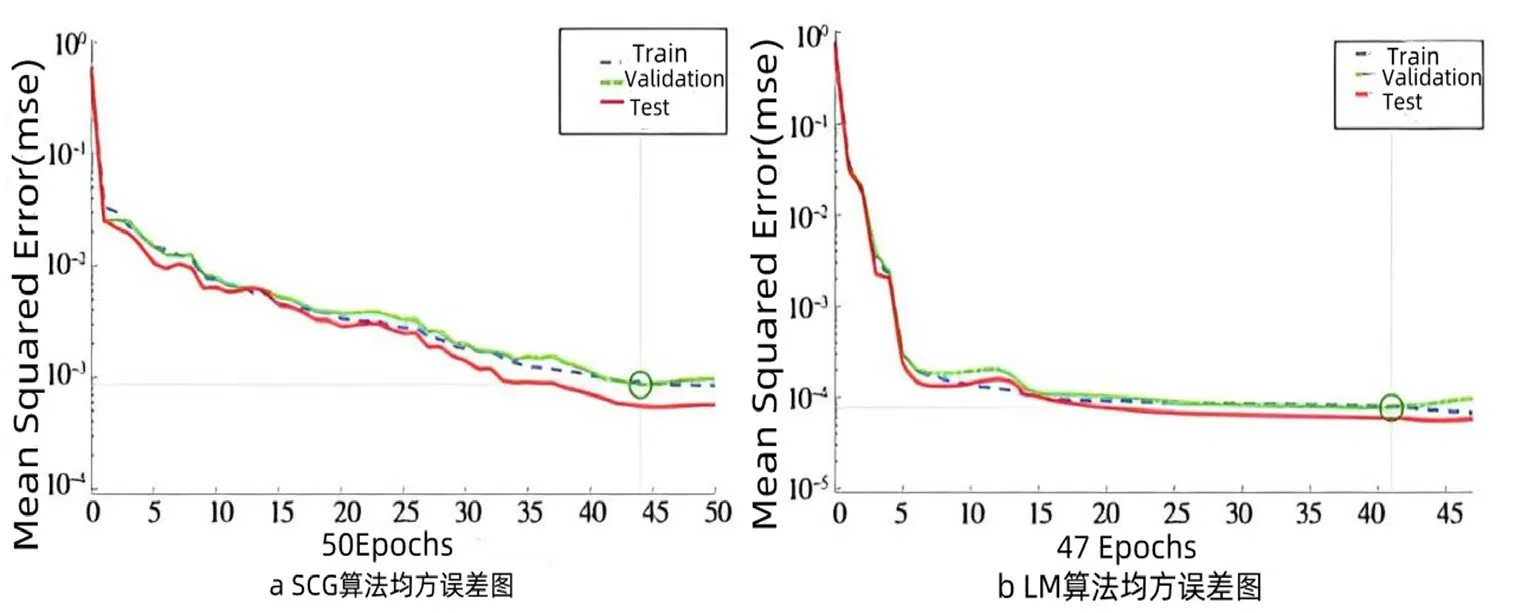
图7 SCG 和LM 算法均方误差图

该模型的预测变异数为0。由图6、图7可知，用LM算法对其进行校正后，所得到的预报误差趋于零，并且具有较高的准确率。因此，本文基于LM算法对光伏组件进行了改进。

对于光伏模块的故障分类，常用的方法有神经网络法和机器学习法，本文选用SCOPSO模型和LM算法来进行分类。在实际应用中，由于光伏发电系统的复杂性与非线性，SCOPSO模型具有很强的全局搜索能力，能快速地找出故障光伏模块。SCOPSO模型与LM算法预测出来的结果基本一致。但不同之处在于SCOPSO模型使用了基于BP神经网络来对故障数据进行训练学习后得到了一个高精度预测值；而LM算法则使用了自适应加权平均法对故障数据进行训练学习，从而得到一个低精度预测值。本文基于SCOPSO模型和LM算法优化了光伏发电系统的故障信息分类方法。利用神经网络建立故障分类模型，结合LM算法提出了一种改进的分类模型[10]。

3.3 评价预报模式的精确度

我们将不同故障等级的光电元件进行分类（表2），并使用平均绝对百分比误差和平均偏差来评估BP神经网络模型。同时，我们分析了在不同故障等级下，该模型如何准确地估计光伏组件的输出功率。从表2中可以看出，无论出现何种故障，该模型的平均绝对百分比误差都在4%以内，平均偏差在0.01以内。

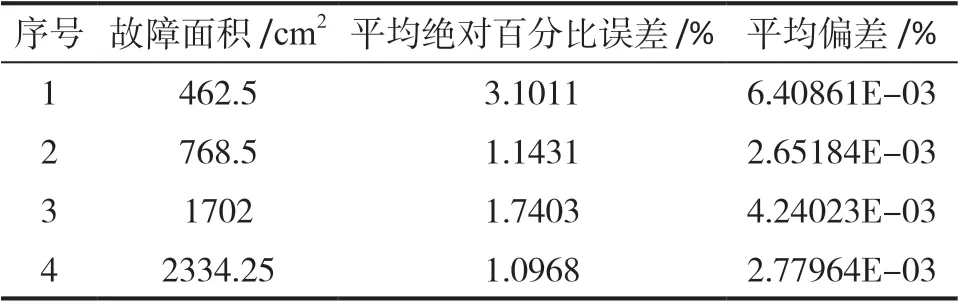
表2 不同故障程度下光伏组件对预测模型准确性的评估

4 结论

为了解决BP网络中存在的主要问题，本研究对改进后的LM和SCG算法进行了比较。结果表明：在最大功率跟踪状态下，光伏阵列输出功率随故障程度增加而增大；故障程度增加时，光伏阵列输出功率受外界环境影响较大，且故障程度越严重，对光伏阵列的影响越大。本文的研究内容主要是通过理论分析得出的结论，并不能完全反映实际情况下的光伏阵列运行特性。