基于KNN算法的高校困难生认定研究
2023-11-16刘晓娜王恺王成德杨进军
刘晓娜,王恺,王成德,杨进军
1.兰州文理学院,甘肃兰州,730010;2.甘肃华科信息技术有限公司,甘肃兰州,730010
0 引言
高校困难生识别是指通过一系列的调查和评估,准确地确定哪些学生符合贫困生的认定标准,以便学校能够提供更有针对性的资助和帮助,帮助他们完成学业,促进学生的发展。而高校学生的经济状况主要由原生家庭所决定,传统的评定方式采用学生自己填表,再结合人工评定的方式来完成。该方式在新环境下开始暴露出一定的弊端,如人为干预、班内拉票等。因此,在助学系统中,我们期望能提出一种人工与计算机结合的方法,先由评定人员制定规则,再由计算机对数据进行识别,认定贫困生并划分困难等级,按等级进行资助。
贫困生的计算机认定过程主要依托于对困难学生数据的分类,认定等级分为一般困难、困难、特别困难三类。在获取到基本数据后,贫困生的认定就转变成按照学生信息字段进行分类的问题。大多学者在分类时,选择了基于K-means的聚类算法,将学生划分为不同的消费群体,或者采用K邻近算法建立预测分类模型,再结合概率分布进行反馈。目前已有的研究技术如下:基于集成学习算法的校园贫困生精准识别,借助数据挖掘技术采用XCB模型作为评估模型;在分布式环境下利用GBDT决策树分类算法对贫困生进行分类;基于稀疏贝叶斯学习的贫困学生识别算法,利用已有贫困学生信息数据训练模型;使用优化SVM算法,在特殊类型数据识别方面取得了较大的改进[1]。各种算法在模型上各有优缺点,但均依托于机器学习,能够高效地实现大数据处理。所以,贫困生的模式识别在大数据技术上,借助遗传算法等工具,是完全具有可行性的。其中,已被证明效率较高的一种方法是使用K近邻(KNN)算法。
1 KNN技术简介
KNN是一种有监督的机器学习算法,可用于根据数据点与其他数据点的相似性对数据点进行分类。该算法的工作原理是找到给定数据点的k个最近邻居,然后使用这些邻居的标签来对未标记的观察数据点进行分类[2]。在计算时,每一次计算当前数据点与样本所有点的距离,然后由近到远排序,选取最近的k个点,这k个点中属于哪一类的最多,就认为该组数据属于哪一类。该算法易于实现,可用于分类和回归任务。执行过程如图1所示。
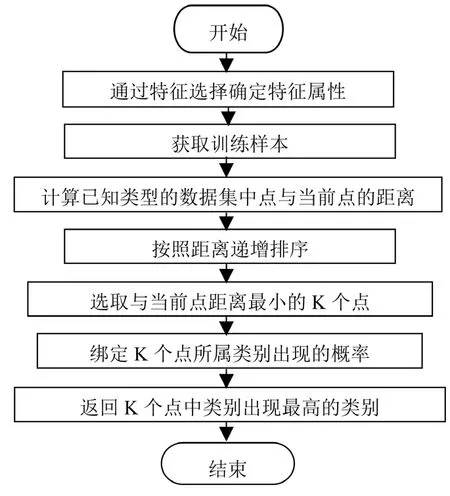
图1 KNN 执行过程图
2 KNN算法的优缺点
2.1 KNN算法的优点
该算法在识别贫困大学生方面有几个优点。首先,该算法易于实现,可用于分类和回归任务,这使得它易于用于各种应用。其次,该算法是非参数的,这意味着它不需要任何数据的先验知识,这使得它适用于数据不被很好理解的应用。再次,该算法对噪声和异常值具有鲁棒性,这意味着即使当数据有噪声或包含异常值时,它仍能产生准确的结果。最后,该算法计算效率高,这意味着它可以在相对短的时间内用于对大型数据集进行分类[3]。
2.2 KNN算法的缺点
尽管KNN算法有优点,但在识别贫困大学生时,它也有一些缺点。首先,该算法对k的选择很敏感,这意味着结果的准确性可能会根据k的值而变化,这意味着为数据集选择合适的k值很重要。其次,该算法不适用于高维数据,意味着它可能无法准确地对分布式环境中的数据点进行分类。再次,该算法不适合具有缺失值的数据,这意味着它可能无法准确地对具有缺失值的数据点进行分类。最后,该算法不适用于具有非线性关系的数据,这意味着它可能无法准确地对具有非线性关系的数据点进行分类。
2.3 几种常用的改进KNN算法
总的来说,KNN算法是一种简单有效的分类方法,它可以应用于多个领域的问题,但也存在一些缺点,如计算复杂度高、受数据维度影响等。针对这些问题,研究人员提出了许多改进算法,如距离加权KNN算法、局部加权KNN算法、混合KNN算法等,这些算法在一定程度上提高了KNN算法的分类精度和计算效率,对实际问题的解决也起到了积极的作用[4]。
(1)距离加权KNN算法。该方法基于不同邻居与数据点的距离为不同邻居分配不同的权重。这可以通过给更近的邻居赋予更多的权重来帮助提高算法的准确性。该算法的工作原理是找到给定数据点的k个最近邻居,然后使用数据点的属性对数据点进行分类。具体工作中,加权KNN算法通过为每个数据点的属性分配权重,这些权重用于确定分类过程中每个属性的重要性。例如,如果学生的学习成绩比他们的财务状况更重要,那么学习成绩属性将被赋予比财务状况属性更高的权重,这允许算法在对数据点进行分类时关注最重要的属性。
加权KNN首先获得经过排序的距离值,再取距离最近的k个元素。在处理离散数据时,将这k个数据用权重区别对待。在处理数值型数据时,并不是对这k个数据简单地求平均,而是加权平均:通过将每一项的距离值乘以对应权重,然后将结果累加。求出总和后,再对其除以所有权重之和。
在某问题分析中,设各因素的权重值为qi,权重反映了各个因素在分类时所占的地位和所起的作用,可凭经验直接给出,但这种方式过于主观性,评判结果可能失真。为保证公平公正,可采用专家预测法来确定权重。设有k个专家独立地给出因素值,如表1所示。
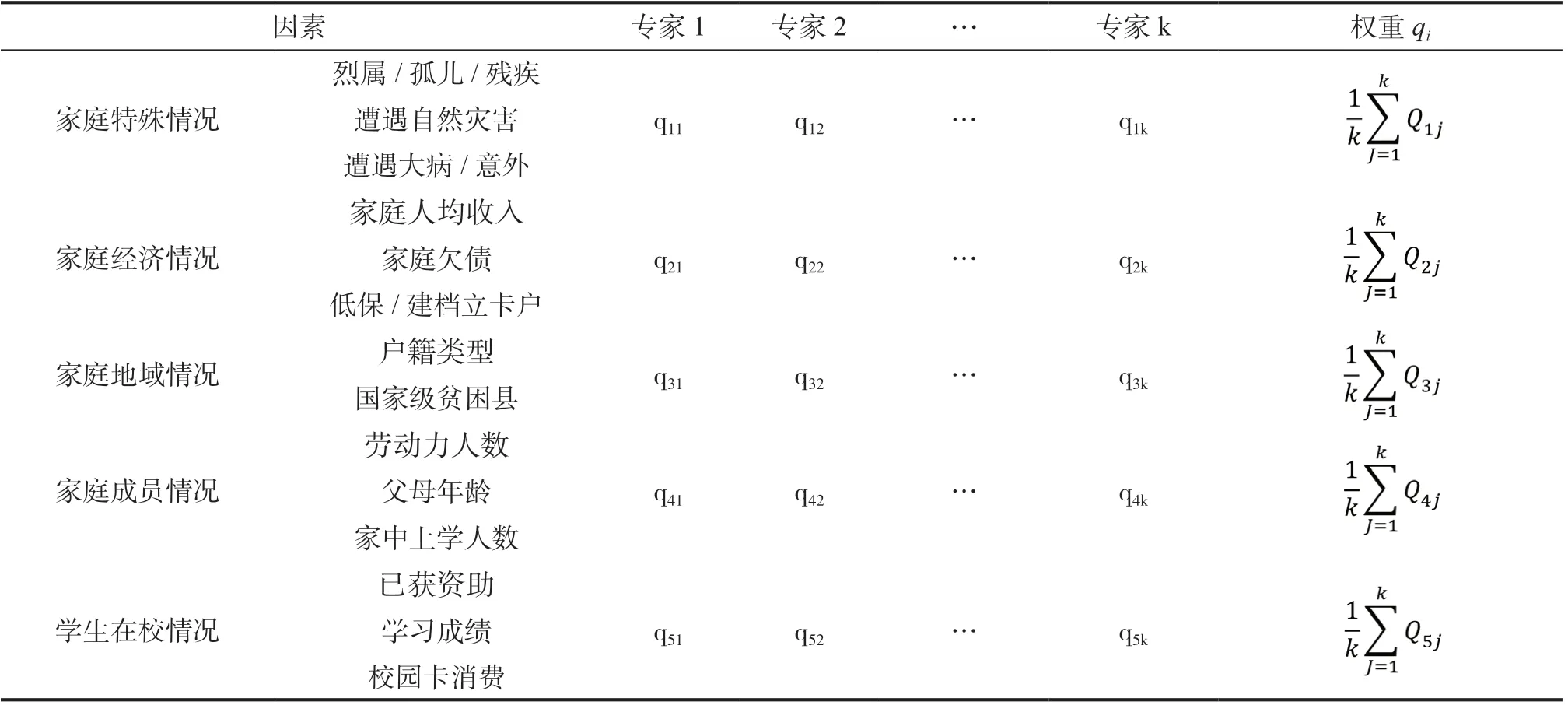
表1 专家-因素权重独立评估表
在得出权重值qi后,设当前节点x与邻居节点xi的距离为欧几里得距离Di,则Di值计算如下式所示,m为原始数据样本数:
f(x)是当前加权分类的数值型结果,计算公式如下式所示:
实现关键代码如下:
/*注释:创建加权KNN函数q-knn,根据前k项估值,采用加权KNN算法计算f(x)的值,qf(x)为计算出的各评价因素的权值*/
var q-knn(k,qf(x)=weight):
var q-knn(data,vec1):
/*注释:按照距离值经过排序的列表f(x)*/
f(x) = getdistances(data,vec1);
avg = 0;
total_weight = 0.0
for i to range(k)
{(dist,id) = x[i];
weight = qf(dist);
avg= avg +data[id]['result']*weight;
total_weight = total_weight +weight;
avg = avg/total_weight; }
return avg;
return q-knn;
通过加权KNN算法,可通过分析学生的学习成绩、家庭经济状况和其他主要相关因素来更好地识别需要帮助的学生。
(2)局部加权KNN。该方法也是一种基于距离加权的改进k近邻方法。不同的是,普通KNN算法是对全部的样本计算,而局部加权k近邻算法,通过引入权值,即核函数的方式,在预测的时候,只使用与测试点距离相近的部分样本来计算回归系数。该算法的工作原理是分析给定学生的数据点,然后使用数据点的属性和权重将学生分类,使用核来对附近的点赋予更高的权重,核的类型可以自由选择,权重计算一般使用简单的高斯核函数等方法。设x为样本数,xi为其中第i项数据,则本次的高斯核计算如下式所示:
其中w是一个对角方阵,方阵大小与x的样本数量相等,计算每一个样本点的时候都要计算一次w矩阵。一个均值为x、标准差为k的高斯函数,与测试样本x越近的样本点,能够得到更高的权重,而远的点则权重很小,以此来提高模型对局部特征的刻画能力。该算法对数据的差异进行放大,适用于数据量大、原始数据差异较小的环境[5]。
(3)混合KNN算法是一种将多个KNN分类器集成起来的方法,它通过对不同的KNN分类器进行加权,以获得更好的分类精度。混合KNN算法可以使用多种不同的KNN分类器,如不同的距离度量方法、不同的k值等,通过对这些分类器进行加权,可以有效地提高模型的分类精度,缺点是需要确定的参数较多,算法实现比较复杂[6]。
3 实验结果对比
利用随机生成的原始数据集,按KNN算法实验,如表2所示。实验软件采用MATLAB,操作系统为Win10,内存4G,CPU i7。对于测试数据中的每一个实例,MATLAB中可以借助Class包中的KNN()函数来实现分类,该函数使用欧氏距离来标识k个近邻,以一个单独的因子向量来存放数据标签,通过k个近邻的投票来对测试的数据进行分类认定。按照二分类的结果,一般k取奇数,可消除各类票数相等的可能性,如训练数据有500条,那么可尝试k为23,该值为素数,且为接近500的开方的奇数。实验中,对随机生成的原始500个数据,分别采用加权k近邻和局部加权k近邻算法进行聚类分析。原始数据如图2所示,实验1按照加权KNN的分类结果如图3所示,实验2按照局部加权KNN所得结果如图4所示。

表2 KNN 算法下的数据实验表

图2 原始随机数据集
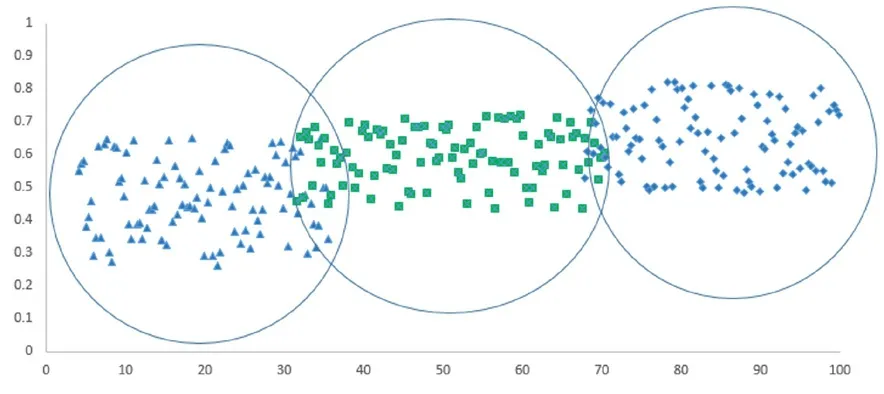
图3 采用加权KNN 算法得到的分类结果
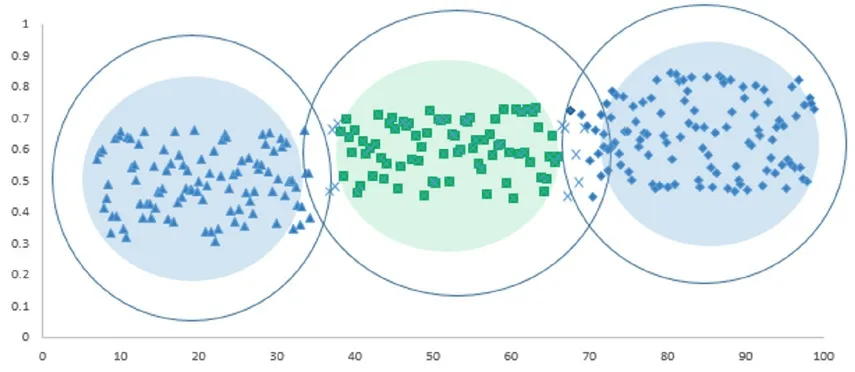
图4 采用局部加权KNN 算法得到的分类结果
由图3、图4可见,采用KNN算法,不论是加权k近邻还是局部加权k近邻,都可以较好地对数据进行分类。数据之间的聚合度好、聚类清晰,可有效地将贫困生按数据分为特别困难、困难和一般困难三类,算法运行时间也在6秒以内,性能良好[7]。
4 结语
综上所述,KNN算法可用于识别贫困大学生。该算法具有简单、对噪声和异常值兼容以及计算效率高等优点。然而,该算法也有一些缺点,包括对k值的选择比较敏感,无法处理高维数据,以及无法处理缺失值和非线性关系的数据等。实践证明,KNN算法可用于准确识别贫困大学生,对实现教育的精准扶贫具有一定的应用价值。
