面向资源约束项目调度的二阶段帝国竞争算法
2023-11-16黄起彬
李 斌,黄起彬
1.福建理工大学 机械与汽车工程学院,福州 350118
2.福建理工大学 福建省大数据挖掘与应用技术重点实验室,福州 350118
3.福建理工大学 交通运输学院,福州 350118
资源约束项目调度问题(resource-constrained project scheduling problem,RCPSP)[1]研究的是如何在有限资源和优先级关系的约束下寻求最佳的活动调度计划,以期实现项目工期的最小化。该类问题是调度领域中最为经典且最具挑战性的组合优化问题之一,许多工程应用问题本质上都可归结为资源约束项目调度问题,如建筑业、流水工作车间和装配生产调度等,长久以来一直是学术界和工程应用研究的重要课题[2-3]。
精确算法、启发式算法和元启发式算法是当前研究和应用中最主要的三类优化方法[4]。精确算法,如分支定界法[5]、关键路径法[6]和整数线性规划[7]等,可精确地求得实例问题的最优解,但由于其较高的计算成本,仅在小规模实例上具有竞争力[8]。启发式算法主要分为基于优先级规则的启发式[9]和基于邻域搜索策略的启发式[10]两类,其最大的优势是能够以较少的计算成本获取较高质量的解决方案,但单种启发式算法适用的问题类型较为有限[11]。元启发式算法,如群聚智能算法[12]和进化算法[13]等,有着更为出色的优化精度和广泛的适用性,以及强大的可拓展性,近年来更多地受到国内外专家学者们的关注[8]。本文提出的二阶段演化帝国竞争算法(two-stage evolutionary imperialist competitive algorithm,TSE-ICA)正是一种能够利用小规模种群有效求解经典RCPSP的元启发式算法。
TSE-ICA将整个演化过程分为两个阶段,分别以种群多样性的开发和高效的收敛为前后两阶段的搜索重点。该算法以探索阶段开始,采用基于关键路径法的组块提取策略构建组块间同化算子,对精简后的搜索空间进行广泛勘探;随后的深度挖掘阶段,采用一种结合相同元素保留策略的组块间同化算子,将优化问题划分为多个以组块内最优为目标的子问题,实现收敛过程稳步且高效的推进。组块提取策略同样被用于革命机制,两种基于子问题的邻域搜索策略被用于增强种群的搜索效率和帮助算法跳出局部最优。同时,帝国竞争机制通过交互各帝国之间的收敛信息,自适应地为各帝国调整同化参数。最后,记忆库[3]作为一种有效的收敛辅助工具被用于提高种群的进化速率。
为了系统性地验证TSE-ICA对经典RCPSP的求解能力,本文选择PSPLIB(project scheduling library)[14]中的实例集J30、J60和J120进行数值实验。首先,采用Taguchi法[15]确定TSE-ICA面对不同实例集时的最佳参数设置。接着,基于PSPLIB提供的当前已知最优解得到的实验结果,与3 种基于帝国竞争算法(imperialist competitive algorithm,ICA)的同源改进算法和其他3种先进的元启发式算法对比,来验证改进机制的有效性和运行效率。最后,基于关键路径值求得的实验数值,与11 种著名的优化算法进行对比,初步说明了TSE-ICA的适用性和优化能力。
1 问题描述
RCPSP中,单个项目是由一个活动集合J、一个代表活动执行优先级的紧前关系集合Pr和一个资源集合K构成。活动集合J中包含n+2 个活动,任一活动j(j=1,2,…,n+2)都有一个紧前活动集合Prj、工期dj和开始时间sj,以及执行过程中对第k类资源的占用量rjk(k=1,2,…,K)。第k类资源的总量上限记为Rk(k∈K)。其中,活动1和活动n+2 为虚拟活动,不消耗时间和资源,用以标记项目的开始与结束,故d1+dn+2=0,r1k=r(n+2)k=0(k=1,2,…,K)。
RCPSP的数学模型如下:
目标函数(1)是最小化项目完成时间,活动n+2的结束时间(FTn+2)即是项目完成时间;约束(2)为优先级约束,任一活动的开始时间大于或等于所有紧前活动的结束时间;约束(3)为资源限制,任一时刻的资源占用量不得超过可用资源上限,其中集合A(t)包含t时刻所有正在执行的活动;约束(4)表示任一活动的开始时间都不为负数。
项目常用一个AoN(activity-on-node)有向网络图G=(N,A)来表示。节点集合N对应n+2 个活动,连接集合A对应活动间的紧前关系。图1是一个由9个活动组成的RCPSP示例,其仅涉及1类资源,该资源为可再生资源[14]且占用上限为8个资源单位。图2为该示例的最佳调度计划,对应的最短项目工期为13个时间单位。
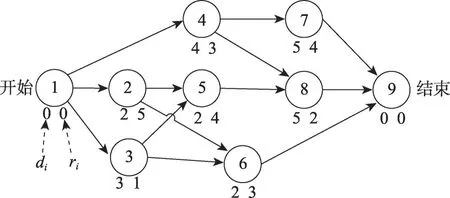
图1 RCPSP实例Fig.1 RCPSP example
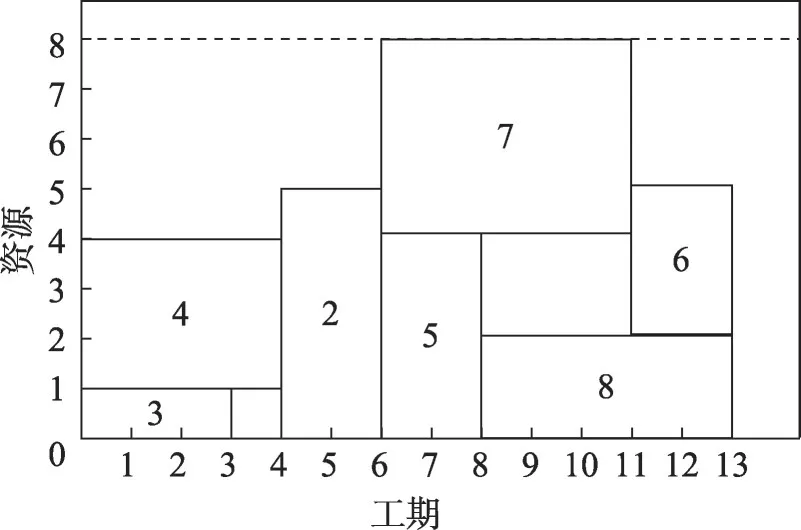
图2 RCPSP示例的最优解决方案Fig.2 Optimal solution of RCPSP example
2 相关工作回顾
2.1 基于元启发式的优化方法
2.1.1 概述
元启发式算法具有优秀的探索寻优能力,但其算法设计和实现中也存在三个需要克服的困难:(1)元启发式算法的随机搜索特性令其难以保证求得精确解,尽管当前已有不少相关算法展现出了强大的优化能力,但它们在开放实例库上的求解精度依然与最优解下限或理论最优解有一定差距;(2)元启发式算法的求解精度与计算耗时往往难以兼顾,二者符合“没有免费的午餐定律”(no-free-lunch theorem)[16];(3)元启发式算法的参数敏感性使其面对不同规模或特性的问题时需要频繁地调整参数来维持算法的鲁棒性。
针对上述挑战,基于元启发式的混合型算法(hybrids)[3]框架在近二十年来获得飞速发展。通常,一种混合型算法框架内同时包含多种算法、搜索算子或优化技术,因此构造一个混合型算法往往运用到多种方法。典型的构造方法有:(1)超启发式,用一种高层启发式对多种底层算法进行选择[17-19];(2)混合算法,将多种元启发式算法结合[20-22];(3)多重算子,为算法引入其他的启发式或元启发式搜索算子[23-25];(4)异构算子,改变搜索算子的演化行为[26-27];(5)异构算法,改进算法的演化框架[28-31]。这些方法使得演化种群能够在迭代过程中采取合适的搜索方式,以满足不同演化阶段下对种群多样性或收敛性能的需求[28]。但是,算法框架的复杂化是计算成本增加的重要原因之一。对于这一问题,不少专家学者选择通过设置较小的种群规模来平衡算法的计算复杂度[4]。
接下来,本节将回顾国内外学者如何基于各类经典的元启发式算法实现混合型算法框架的构建,以求解RCPSP及其衍生问题。
2.1.2 进化算法
Kadri等[26]提出一种能有效求解多模式RCPSP的遗传算法(genetic algorithm,GA),通过将优先级规则与基于遗憾值的有偏取样策略[10]结合,生成高质量的初始种群,同时采用一种改进的两点交叉算子以更加适用RCPSP 的求解。Sallam 等[28]将整个迭代过程分为以种群多样性与局部收敛为主要搜索目标的前后两个阶段,提出一种两阶段、多算子的差分进化算法(differential evolution,DE),该算法在每个阶段设置两种差分进化算子,并根据不同算子对多样性和收敛的贡献程度对搜索算子进行选择。项前等[29]提出一种差分进化参数控制及双向调度算法,在差分进化算法的基础上加入自适应参数控制策略、正逆向交替调度优化(forward-backward improvement,FBI)[32]策略和一种保留精英个体的种群随机重建策略,以尽可能满足RCPSP对算法性能的要求。
2.1.3 群集智能算法
Dang 等[30]为了避免算法后期陷入局部最优,在粒子群优化算法(particle swarm optimization,PSO)中引入一种迁移策略,该策略能够将收敛停滞的种群转移至新的区域探索,以此跳出局部最优。Chen等[23]为了加快PSO算法对最优解的搜索效率,对每次迭代产生的新个体执行活动延迟邻域搜索策略和FBI,通过提高种群对解空间的取样数量,提高算法寻得最优解的概率。安晓亭等[24]首先对蚁群算法(ant colony optimization,ACO)进行适应性改进并求得Pareto 解集,接着利用带逻辑约束的insert 和swap局部搜索启发式对当前种群中的非支配解进行邻域搜索。Ziarati 等[25]同时对蜜蜂算法(bee algorithm,BA)、人工蜂群(artificial bee colony,ABC)算法和蜂群优化(bee swarm optimization,BSO)算法拓展三种局部搜索策略,并通过实例集J30、J60、J90和J120的测试实验证明结合了FBI 的BSO 是实验所涉算法中优化性能最好的变种算法。
2.1.4 混合算法
Myszkowski 等[20]提出一种将差分进化算法与贪婪局部搜索(greedy local search,GLS)算法结合的混合算法,该算法通过由DE 产生子代,再由基于GLS的调度生成策略为子代个体生成最优的调度计划。Tian等[21]采用相同思路,采用GA生成子代,然后混合一种基于多目标马尔可夫网络的分布估计算法(estimation of distribution algorithm,EDA),为子代建立资源分配模型,进而帮助每个子代个体获得最优的调度计划。Bagherinejad等[22]提出一种新型混合算法,将非支配排序蚁群优化(non-dominated sorting ACO)算法与GA 相结合,以实现对具有时间不确定性的RCPSP的鲁棒调度。
2.1.5 基于元启发式的超启发式算法
结构较为简单的超启发式算法根据概率随机选择底层算法。Elsayed 等[4]以多算子遗传算法和多算子差分进化算法为底层算法,构建一种通过自适应概率系数对4 种底层搜索算子进行选择的超启发式算法COA(consolidated optimization algorithm)。COA将迭代过程分为多个周期,每一周期开始前会重新选择搜索算子,而每种搜索算子的被选择概率会根据之前的收敛表现进行适用性调整。
基于强化学习的超启发式,通过深度学习技术不断学习底层算法在执行过程中的历史表现,以决定每一种底层算法在下一决策点被选择的概率。Sallam等[17]以多算子差分进化算法和禁忌搜索(cuckoo search,CS)为底层算法,提出一种基于强化学习策略的超启发式算法DECSwRL-CC(DE and CS with reinforcement learning with chance constrained)。
还有一种常见的超启发式设计范式,是将底层算法的选择优先级视作优化问题,以元启发式算法作为高层算法对其进行求解。Koulinas 等[18]提出一种基于粒子群优化算法的超启发式算法,采用PSO对8 种启发式搜索算子进行选择;Chand 等[19]提出了以9种优先级规则为底层架构的遗传规划超启发式,利用GA 的交叉算子和变异算子挑选适合求解当前问题的优先级规则。
2.1.6 面向RCPSP的其他典型算法改进
Wang 等[27]针对RCPSP 提出一种混合估计分布算法,采用一种新型概率模型更新机制对有挖掘潜力的搜索区域进行更好的采样,同时还引入FBI和基于置换的局部搜索策略来增强算法的收敛能力。Bouleimen等[31]利用两种邻域搜索策略改进模拟退火(simulated annealing,SA)算法,新算法可用于标准RCPSP 和多模式RCPSP 的求解。但是,Wang 和Bouleimen 等提出的这两种算法都没能对标准实例库PSPLIB的实例问题提出较有竞争力的解决方案。
2.2 帝国竞争算法
2.2.1 帝国竞争算法概述
ICA 是由Atashpaz-Gargari 和Lucas 于2007 年提出的一种群集智能算法[33],其计算流程如算法1 所示。首先,生成一个个体规模为NP的初始种群Pop0={Xi|i=1,2,…,NP},其中Xi为个体矢量,对应优化问题的一个可行解,Xi的成本值(即适应度)为f(Xi)。挑选Pop0中成本值最低的Nimp个解作为帝国主义国家,其余解则作为殖民地分配给各帝国主义国家,组成多个帝国。随后,各帝国在迭代过程中循环执行同化、革命、交换和竞争四种机制。失去所有殖民地的帝国将会消亡。当种群中仅剩一个帝国或算法达到最大迭代数时,结束运行,输出种群中的最优个体。
算法1帝国竞争算法
输入:帝国竞争算法参数(NP,Nimp,β,γ,UR)。
输出:种群中的最优个体Xbest。
步骤1随机生成一个规模为NP的初始种群Pop0。
步骤2帝国划分。Pop0中最优的Nimp个解成为帝国主义国家,计算和比较各帝国主义国家的归一化成本值cˉ,任一帝国e可获得的殖民地数量为Ncole(e=1,2,…,Nimp)。
步骤3同化。所有帝国内,殖民地根据β和γ向其隶属的帝国主义国家所在区域移动。
步骤4革命。为帝国内的每一个殖民地生成一个0到1之间的随机数ri,ri小于UR的殖民地将被重新随机生成(i=1,2,…,Ncole)。
步骤5交换。帝国中成本值最低的国家成为该帝国的帝国主义国家。
步骤6竞争。归一化总成本值最小的帝国将其最弱的殖民地供给其余帝国争夺,计算其余帝国的势力POWe=[-re],势力最大的帝国获得该殖民地。
步骤7算法达到终止条件前重复执行步骤3至步骤6。
ICA中,帝国所代表的子种群之间属于平行合作[3]关系。帝国内部通过同化、革命和交换三个机制进行演化,帝国间的交互由竞争机制完成。同化机制中,殖民地根据同化系数β和同化偏移角γ向其隶属的帝国主义国家移动,以通过对帝国主义国家邻域的大量采样实现搜索区域的快速收敛。根据革命概率UR,革命机制会重置部分殖民地的个体编码,帮助种群保持多样性。交换机制确保每轮迭代开始时帝国主义国家是帝国内部成本值最低的个体。竞争机制根据各帝国的总成本值TC(total cost),通过将弱势帝国的最弱殖民地转移给演化效益更高的帝国,来强化种群对关键区域的收敛效率。更详细的算法流程和参数说明请查阅文献[34]。
2.2.2 帝国竞争算法在调度问题中的应用
目前,ICA 还鲜有被用于RCPSP 及其衍生问题的求解,但大量的文献资料显示,ICA 有着较强的搜索性能和鲁棒性[35],且在调度优化领域有着良好的应用潜力,如:Li 等[36]开发出一种具有动态反馈能力的ICA,为考虑运输与时序的流水车间调度问题提供了一种有效的解决方案;Akbari等[37]成功利用ICA实现VVER-1000 反应堆堆芯在循环期间的最佳燃料布置;Behjati 等[38]采用一种分组式帝国竞争算法,处理大规模码头岸桥分配和内集卡调度问题,在对实例的计算中取得了良好效果;Shokouhandeh等[39]利用一种改进ICA,面向电动汽车停车场与采用分布式发电单元供能的充电桩,实现两种应用场景下的24 h 能源优化调度。总的来说,ICA在调度领域有着广泛的应用前景,且还有很多细分领域未曾涉猎。基于此,本文尝试提出一种TSE-ICA用于RCPSP的求解。
3 二阶段演化帝国竞争算法
TSE-ICA是一种针对RCPSP所提出的具有多个搜索算子和优化策略的混合型优化算法。如前所述,该算法将优化过程分为勘探与挖掘两个阶段,通过在不同阶段选择合适的搜索算子,实现种群多样性与收敛性能的灵活侧重。本文创新性地提出两种新型同化算子用于二阶段演化框架的构建。同时,采用记忆库技术异构化ICA的种群演化模式。
TSE-ICA的优化流程如图3所示。首先,采用随机数排序法[29]和编码修正策略(算法2)生成初始种群,利用串行调度生成策略[40]计算个体成本值,并为初始种群划分帝国。接着,建立一个与初始种群规模相当的记忆库M,将初始种群存于其中。至此种群开始迭代,并根据预设的迭代数将演化过程分为两个阶段:阶段1,采用组块间同化算子开发种群多样性;阶段2,在组块间同化算子中融入相同元素保留策略以加速收敛。同时,基于组块的改进革命机制能够有效地对殖民地进行邻域搜索。而改进后的帝国竞争机制可以交互各帝国的收敛信息,自适应地调整各帝国的同化系数。同化机制和革命机制产生的高质量子代会取代M中的较差解。在每一轮迭代结束前,使用M更新现有种群,并重新划分帝国。算法达到终止条件(当前迭代数g大于预设的最大迭代数G)时结束运行,输出种群中的最优解。
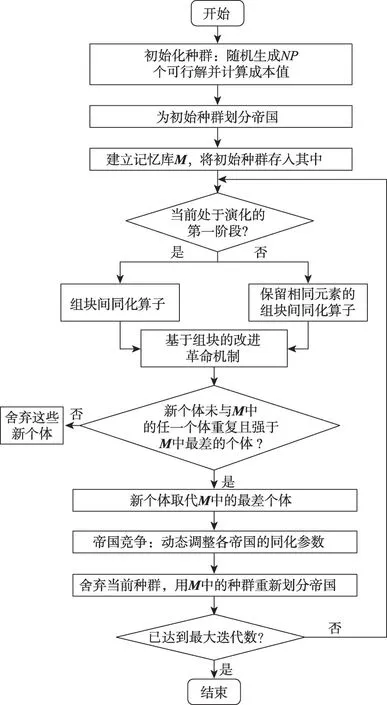
图3 TSE-ICA的流程图Fig.3 Flowchart of TSE-ICA
3.1 个体编码与初始种群
TSE-ICA 的Pop0中,个体的编码形式是满足优先级约束的活动列表Xi=(x1,x2,…,xn+2)。初始个体皆由随机数排序法生成:首先,为每一个活动生成一个0 至1 内的随机数,而活动1 和活动n+2 固定对应数值0和1;接着,对所有随机数进行升序排列得到随机数数列,进而生成对应的活动列表;最后,对生成的活动列表采取编码修正策略,得到满足优先级约束的可行活动列表。图4为一个可行解的生成过程。
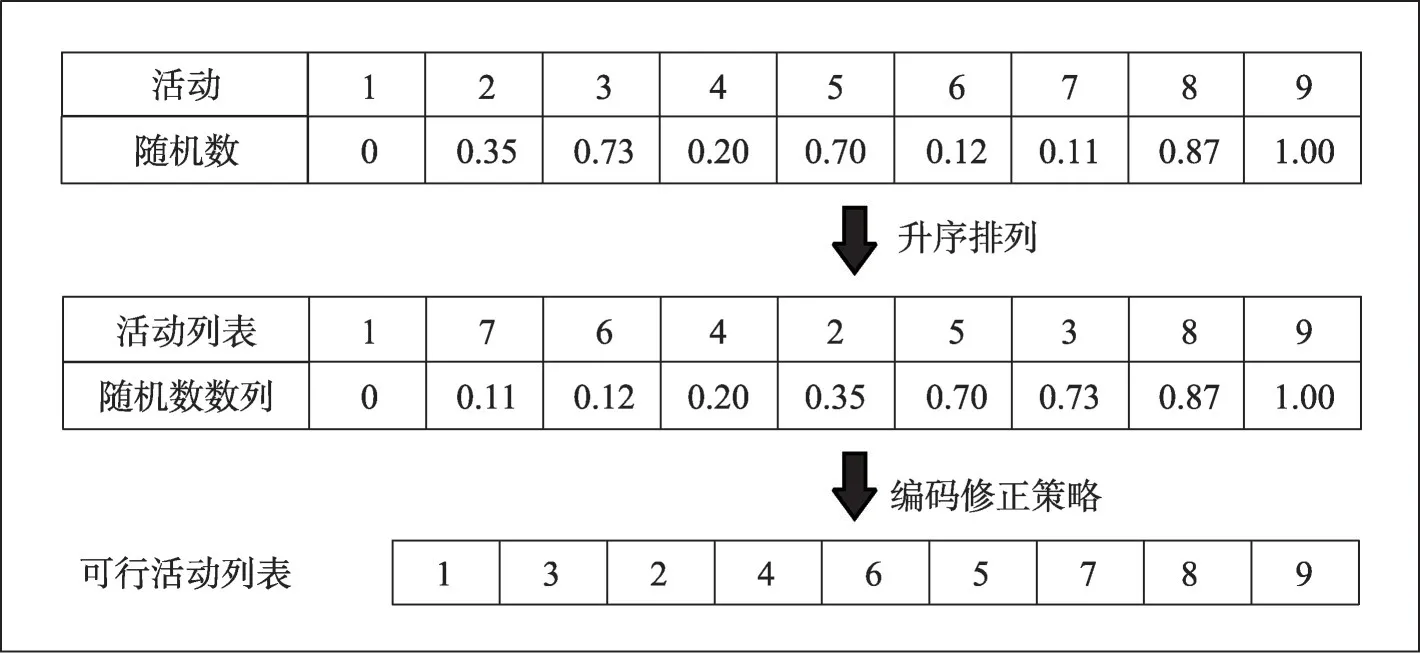
图4 可行活动列表的生成过程Fig.4 Process of generating feasible activity list
算法2 为非可行解的编码修正策略。整个修正过程分为n+2个阶段,每一个阶段针对一个编码位置进行修正。若当前位置的活动不符合优先级约束,便在活动列表中找出该活动的所有紧前活动,然后将该活动与编码位置最靠后的紧前活动调换位置,重复该过程直至当前位置的活动满足优先级约束,便进入下一阶段对下一个编码进行修正。
算法2编码修正策略
初始种群建立后,需要将每个个体编码转换为调度计划方可计算成本值(即项目完成时间)。串行调度生成策略(serial schedule generation scheme,SSGS)和并行调度生成策略(parallel schedule generation scheme,PSGS)是最常用的两种转换方法[40]。基于活动列表中的排序,SSGS能够给予每一个活动尽可能早的开始时间,令每个活动被安排在允许其执行的时间窗内的最佳时刻,因此SSGS生成的调度计划被称为活跃的调度计划(active schedule);PSGS能够在任一时刻t尽可能多地执行活动,在该策略下延迟任一活动的开始时间都会导致项目完成时间被延迟,因此PSGS 生成的调度计划被称为不可延迟的调度计划(non-delay schedule)。不可延迟的调度计划是活跃的调度计划的一个子集,最优解决方案一定存在于活跃的调度计划中。因此,本文选用SSGS计算个体的成本值。
随机生成个体的计算复杂度为O(nNP),编码修正策略和SSGS 的计算复杂度同为O(n2NP),因此初始化种群的计算复杂度为O(2n2NP+nNP)。
3.2 记忆库
在基于种群的元启发式算法中,记忆库是一项常用的收敛辅助工具,更是GA 与DE 及其变种算法的核心组成部分[3]。记忆库能够存储搜索过程中产生的精英解,并利用该信息引导种群进化,进而起到提高种群收敛速度的作用[41]。
为保证种群整体质量的稳定提高,TSE-ICA引入一个记忆库M,用于存储当前质量最高的NP个可行解,并在每一轮迭代结束前用其更新当前种群。迭代开始前,M会对整个初始种群进行备份,且M的存储规模不再发生变化。每一轮迭代中,经由同化机制(3.3节)与革命机制(3.4节)产生的新个体,若不与M中的任一个体重复(即所有活动的开始时间一致)且优于M中的最差解,便取代M中的最差解,反之舍弃这些新个体。最后,在每一轮迭代结束前,现有种群会被M中的种群替代,并重新进行帝国划分。利用记忆库更新种群的计算复杂度为O(NPG)。
需要说明的是,因为本文算法会在每一轮迭代中重置种群并重新划分帝国,所以无需执行标准ICA中的交换机制。
3.3 二阶段同化机制
以探索阶段开始、挖掘阶段结束的二阶段演化框架目前已被运用于多种混合型元启发式算法中,且都取得了较好的实验成果[28,42]。经典的二阶段演化过程常常将寻优过程按照迭代次数分为两个阶段,然后在前后两阶段使用不同特性的搜索算子。同化是ICA最主要的搜索算子。因此,本文提出两种专门用于RCPSP 的改进同化算子,分别负责第一阶段对搜索空间的广泛勘探和第二阶段对最优解的快速收敛。比例系数St控制着两个阶段的转换:当g>St×G时,演化进程由阶段1进入阶段2。
3.3.1 组块间同化算子
TSE-ICA在阶段1,采用组块间同化算子开发种群多样性,即殖民地向其宗主国趋同的过程中,个体的编码分量以组块为单位进行变动来产生新个体。
通过关键路径法[6],可以得到实例网络图G=(N,A)的关键路径和每一个活动对应的最早开始时间EST(earliest start time)和最晚结束时间LFT(latest finish time)。处于关键路径上的活动被称为关键活动,延迟关键活动的完成时间会对项目工期造成直接影响[8]。以关键活动为界,一个活动列表可提取出若干个组块,构成一个组块集合B。图1中的关键活动为1、2、6和9。基于图1,一个组块提取示例如图5所示。在任一可行活动列表内部,关键活动间的前后顺序始终是固定的。因此,将关键活动作为组块的首个元素能够起到标记组块位置的作用,并作为组块的索引号使用。同化双方具有相同索引号的两个组块在本文中被称为对位组块。
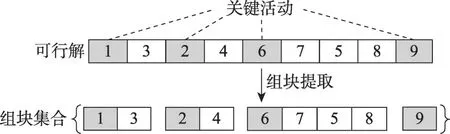
图5 组块提取示例Fig.5 Example of block extraction
上述的组块提取策略能够帮助算法实现特征选择[43],用以较好地去除搜索空间中的冗余部分。关键路径之外的活动被称为非关键活动,由于优先级关系的约束,每一个非关键活动只能进入固定且数量有限的组块中。比对非关键活动与关键活动的EST和LFT,便可得到每一个非关键活动允许进入的组块集合(集合内包含的是组块索引号),如算法3 所示。通过将组块信息与随机搜索过程结合,每一个编码分量的变动范围被限制在符合条件的组块内,即随机搜索行为被限制在可行解所在的子空间内,以此提高算法对解空间的搜索效率。
算法3获取非关键元素的可进入组块集合
基于组块提取策略构建的组块间同化算子,可以利用一个同化概率UA∈[0,1]控制子代的多样性。组块间同化的运算流程如算法4 所示。通过采用0至1 内的随机数与UA进行对比,殖民地个体的每一个非关键活动编码都有三种可能的变动形式:当随机数rj,1>UA时(j∈Jnc,Jnc为非关键活动集合),将待同化的活动从当前所在组块随机移入一个允许其进入的组块的末尾;若rj,1
3.3.2 保留相同元素的组块间同化算子
TSE-ICA的阶段2,采用保留相同元素的组块间同化算子以加速收敛。
随着种群的演化,一些有助生存的基因片段会越来越普遍地存在于个体编码中。对于RCPSP,这些基因片段可表征为多个特定活动有序组成的特定活动块。这些活动块能够高效利用资源、有效压缩工期。但很多传统的优化方法不具备分辨和保护特定活动块的能力,在搜索过程中对其造成破坏,从而产生大量的低质量解[8]。针对这一问题,文献[8]选择将父代双方编码中的相同活动块保留至子代,来改善子代的整体质量。本文受此启发,为组块间同化算子引入相同元素保留策略。
组块本质上就是由若干活动组成的活动块,故优化问题可被拆解为多个子问题:各组块的最优构成。相同元素保留策略通过不变动同化双方在对位组块中的相同元素,并以其在帝国主义国家(种群中的较优解)中的编码顺序传承至子代,实现组块内特定活动块的识别和保留。随着迭代的进行,组块内的特定构成元素会不断地积累和完善,进而实现优化子问题的逐个收敛。因此,相同元素保留策略的加入,能够将父代的优秀特征继承至下一代,保证子代的整体质量。并且,子代在基因上与父代的帝国主义国家更加接近,有助于各帝国更快速地完成邻域空间的收敛工作。
保留相同元素的组块间同化算子的工作流程如算法4 所示。与阶段1 相比,阶段2 的同化算子在执行过程中仅有两处不同:(1)继承至子代个体的特定活动在排序上同帝国主义国家一致(算法4 的步骤2);(2)对位组块中的相同元素不执行同化操作(算法4 的步骤3.1)。此外,算法4 的步骤3.3 中,将活动插入组块末尾同样是为了不破坏已有的特定活动块。并且,由算法4 可得,二阶段同化算子的最大时间复杂度为O[(n2+n+1)NPG]。
算法4二阶段同化机制
3.4 基于组块的改进革命机制
TSE-ICA 的革命机制包含插入和乱序两种领域搜索策略,主要功能是强化算法的搜索速率和避免陷入局部最优。插入策略[3,10,24,28]指将一个活动移动至任意一个允许其进入的组块内的随机一个位置;乱序策略指对组块内的非关键活动进行一次乱序。
阶段1 时,算法需要对搜索空间进行广泛勘探,插入策略和乱序策略能有效提高算法对解空间采样次数。阶段2时,一些基因片段会在演化过程中受到保护和传承。假若这些固定的编码片段尚未拥有最优的元素构成且一直没有被完善,便会在同化机制的趋同作用下普及至每一个帝国成员,进而陷入局部最优。因此,采用插入策略适当地调整组块内的元素构成,及采用乱序策略帮助组块内的元素尝试不同的排序方案,有机率帮助帝国成员跳出局部最优。
改进后的革命机制依旧根据革命概率UR挑选部分殖民地进行变异,具体流程如下:
首先,设置一个变异概率UM,并在殖民地个体对应的组块集合Bcol中随机挑选一个组块,该组块至少包含一个非关键活动。接着,生成一个随机数rcol,若rcol
相比插入策略,乱序策略会同时对更多活动造成影响。而随着演化过程的推进,组块内的元素构成趋于成熟,再对其进行频繁的乱序易造成子代个体的质量低下。因此,受文献[44]启发,UM将随着迭代数的增大而增大,其值由下式确定:
式中,UM,max为变异概率的最大取值。
由以上描述可知,改进革命机制的时间复杂度为O(URNPG)。
3.5 改进帝国竞争机制
由于每一轮迭代都会对帝国势力进行重新划分,帝国间的强弱关系不再适用于引导子种群间的计算资源流动。为了更好地利用不同子种群间的平行合作关系,TSE-ICA的帝国竞争机制通过交互各帝国的收敛信息,自适应地为各帝国设置更适合的同化概率UA。
首先,在初始种群划分帝国后,根据式(6)为每一个帝国设置不同取值的初始UA。
式中,UA,i,1为第i个帝国在第一轮迭代中使用的同化系数;UA,min为初始UA中的最小值。
在演化过程中,各帝国会向上一轮迭代中收敛效益最高的帝国进行学习,自适应地调整UA值;但是,若所有帝国在上一轮迭代中都未能让同化后的殖民地得到提升,各帝国在当前迭代的UA值会逐渐向各自的初始值靠近,以通过更广泛的同化搜索范围帮助种群挖掘出更具潜力的搜索区域。帝国竞争的操作流程如下:
(1)计算各帝国在同化过程中的收敛效益Cb,计算公式如下:
式中,下标g和g-1 用于表示迭代数的前后关系,后同;表示第e个帝国的第i个殖民地;βe,i为同化后降低的成本值,如果殖民地未获得提升,其对应的βe,i=0。
(2)记收敛效益最高的帝国的收敛效益为Cbbest,g、同化概率为UA,best,g。若Cbbest,g>0,收敛效益最高的帝国在下一轮迭代继续使用该UA值,其余帝国则通过式(9)更新UA值;若Cbbest,g=0,表示所有殖民地都未能在被同化后获得提升,此时各帝国用式(10)更新UA值。
式中,N为高斯分布函数。需要注意的是,当UA,i,g+1<0 时,令其值等于0;当UA,i,g+1>1 时,令其值等于1。
由上,可得帝国竞争的时间复杂度为O(NPG)。
3.6 时间复杂度分析
将各组成部分的时间复杂度相加,TSE-ICA的时间复杂度为O{[(2n2+n)+(n2+n+3+UR)G]NP},若只关注主体部分,可将其表示为O(n2NPG)。
表1 为3 种先进的RCPSP 元启发式优化算法与TSE-ICA 的时间复杂度对比。通过如表1 所示的对比结果,可以发现TSE-ICA 有着较为合理的计算成本,这意味着TSE-ICA 对RCPSP 有着较好的应用潜力。同时,经典的ICA源于对连续优化问题的求解,在以往工作中实现过3 种能够较好求解连续优化问题的改进ICA,其与本文所提TSE-ICA的时间复杂度对比如表2 所示。用于组合优化问题的TSE-ICA 相对于以往提出的ICA改进算法,在时间复杂度上有一定的增加,但仍表现出较好的特性(随后的计算实验中得到进一步证明)。

表1 算法时间复杂度横向对比Table 1 Lateral comparison of time complexity
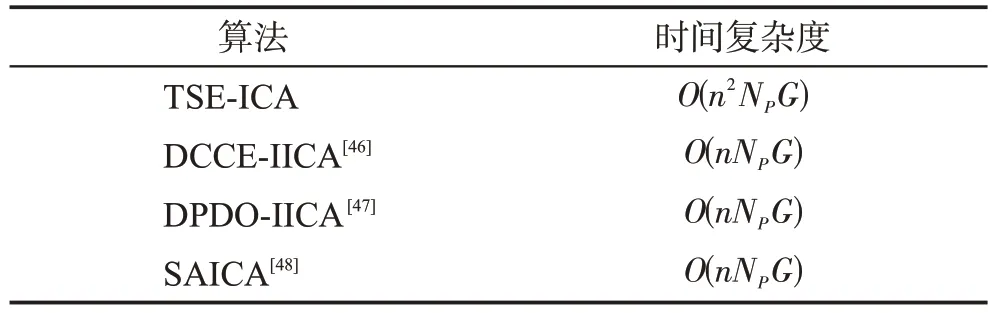
表2 算法时间复杂度纵向对比Table 2 Vertical comparison of time complexity
4 仿真实验与结果分析
4.1 实验设置
本文实验是基于CPU为2.20 GHz i7-10870H、内存16 GB、64位Windows 10操作系统的计算机完成,编程平台为Python3.7。为了检验本文算法的性能特点,仿真实验部分选用标准实例库PSPLIB(http://www.om-db.wi.tum.de/psplib)的3 个实例集J30、J60和J120,共1 560 个实例,其中J30 和J60 皆包含480个实例,J120 包含600 个实例。这些实例的生成与3个参数密切相关[14]:
(1)网络复杂度(network complexity,NC)为每个活动的平均紧前活动数量。
(2)资源因子(resource factor,RF)为每个活动的资源需求量与资源总量的平均百分比。其值越大,活动对资源的平均需求量越大,反之则越小。
(3)资源强度(resource strength,RS)为资源的稀缺程度。其值越大可供调配的资源总量越多,反之资源受限越严重。
J30和J60的参数设置为NC∈{1.5,1.8,2.1},RF∈{0.25,0.50,0.75,1.00}和RS∈{0.2,0.5,0.7,1.0}。而J120除了RS∈{0.1,0.2,0.3,0.4,0.5}外,其余参数与其他两个实例集相同。
为了更好与其他同类型研究进行对比,需要测试最大调度次数Schedules为1 000、5 000和50 000时的实验结果(最大迭代数G=Schedules/NP)。单个实例的独立运行次数为10。实验的评估指标是平均偏差率AD(average deviation),即算法所求最优解与最优下界的偏差。J30 的最优下界为精确最优解。J60和J120 中部分实例的精确最优解未知,针对这两个实例集目前有两种评判标准:
(1)以当前已知最优解作为最优下界求取平均偏差率ADBK:
(2)在国际上更为通用的以关键路径值为最优下界求取平均偏差率ADCP:
式(11)、式(12)中,P为当前实例集包含的实例个数;Fbest,p为算法对实例p多次独立运行后取得的最优解;LBp为实例p的最优下界;下标BK 和CP 用于区分当前已知最优解和关键路径值。关键路径值为不考虑资源约束时的项目最短完成时间。
4.2 参数分析
TSE-ICA中影响算法有效性的参数有:种群规模NP、帝国个数Nimp、最小同化概率UA,min、革命概率UR、最大变异概率UM和阶段转换比例系数St。因为采用小规模种群有效求解经典RCPSP是本次研究的主要目标之一,所以在参照大量相关文献后[4,8],将本次实验中的种群规模NP设为50。
本文采用Taguchi 法的实验设计方法(design-ofexperiment,DOE)[15]确定最佳的参数值。分别从J30、J60 和J120 中随机选取48、48 和60 个实例计算ADBK,实验的最大调度次数为5 000。
表3 为各参数值对应的等级。表4 为参数等级正交表和25种参数组合下TSE-ICA的实验结果。图6是由实验结果得到的参数等级变化趋势,图中ADBK值最低的等级对应着最佳的参数取值。根据图6,TSE-ICA 针对不同实例集的最佳参数组合如表5 所示。表6 统计了面对不同实例集时各参数对TSEICA的影响程度。由表6可知,对于J30,对TSE-ICA的优化性能影响最大的参数是Nimp,最小的是St;对于J60,UR是最有可能影响TSE-ICA 算法性能的参数,其次是UA,min,影响最小的则是St;求解J120 时,TSE-ICA 对UA,min的敏感性最高,对Nimp的敏感性最低。
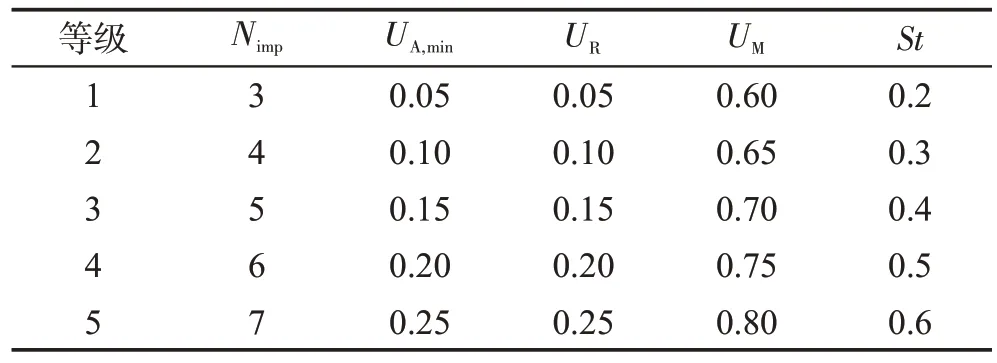
表3 参数取值等级Table 3 Level of parameter values
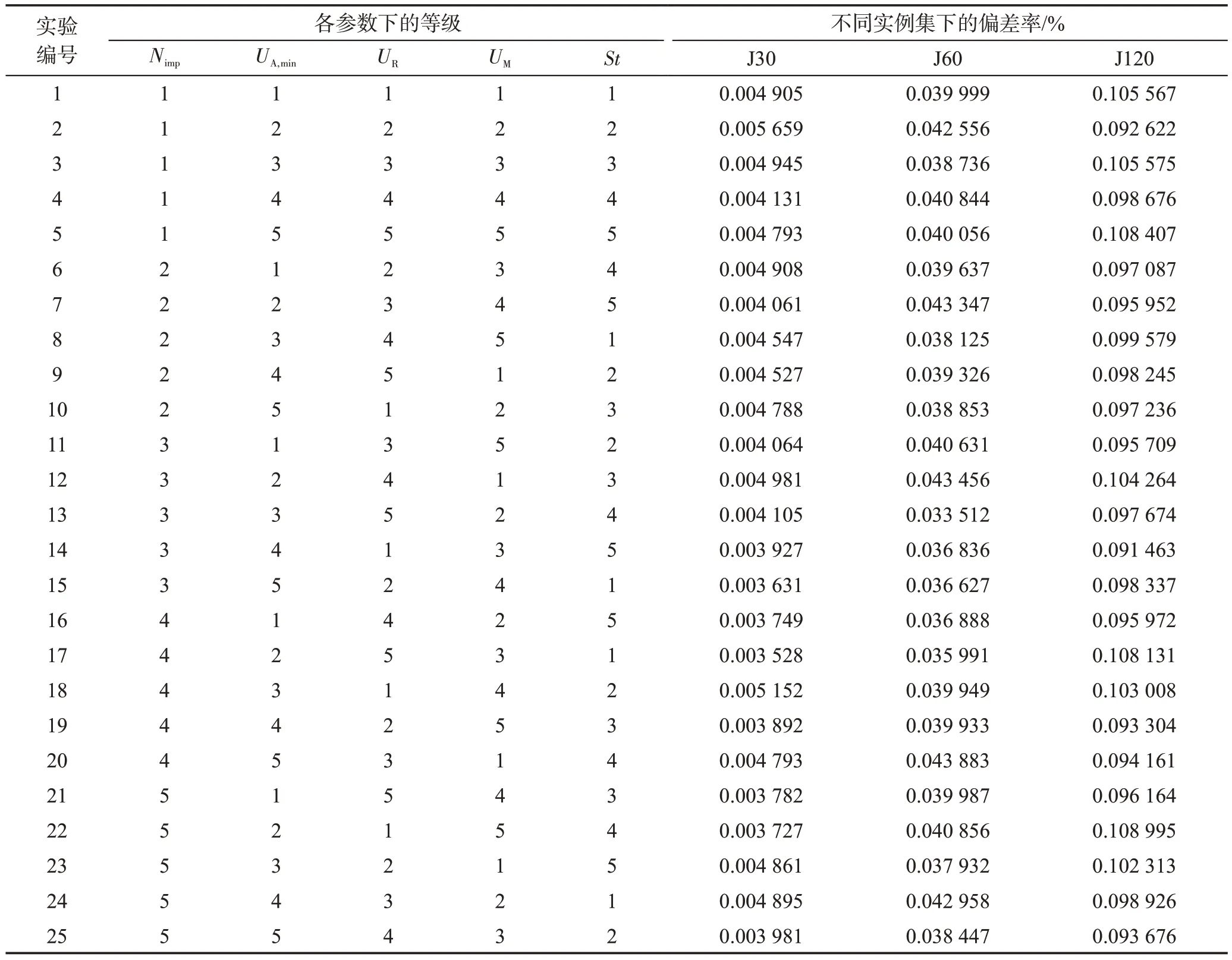
表4 正交表和TSE-ICA求解J30、J60和J120的平均偏差率ADBKTable 4 Orthogonal table and average deviation ADBK of TSE-ICA for J30,J60 and J120
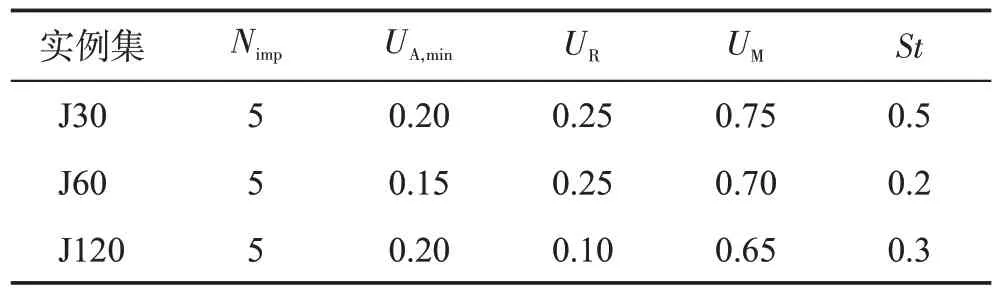
表5 最佳参数组合Table 5 The best combination of parameter values
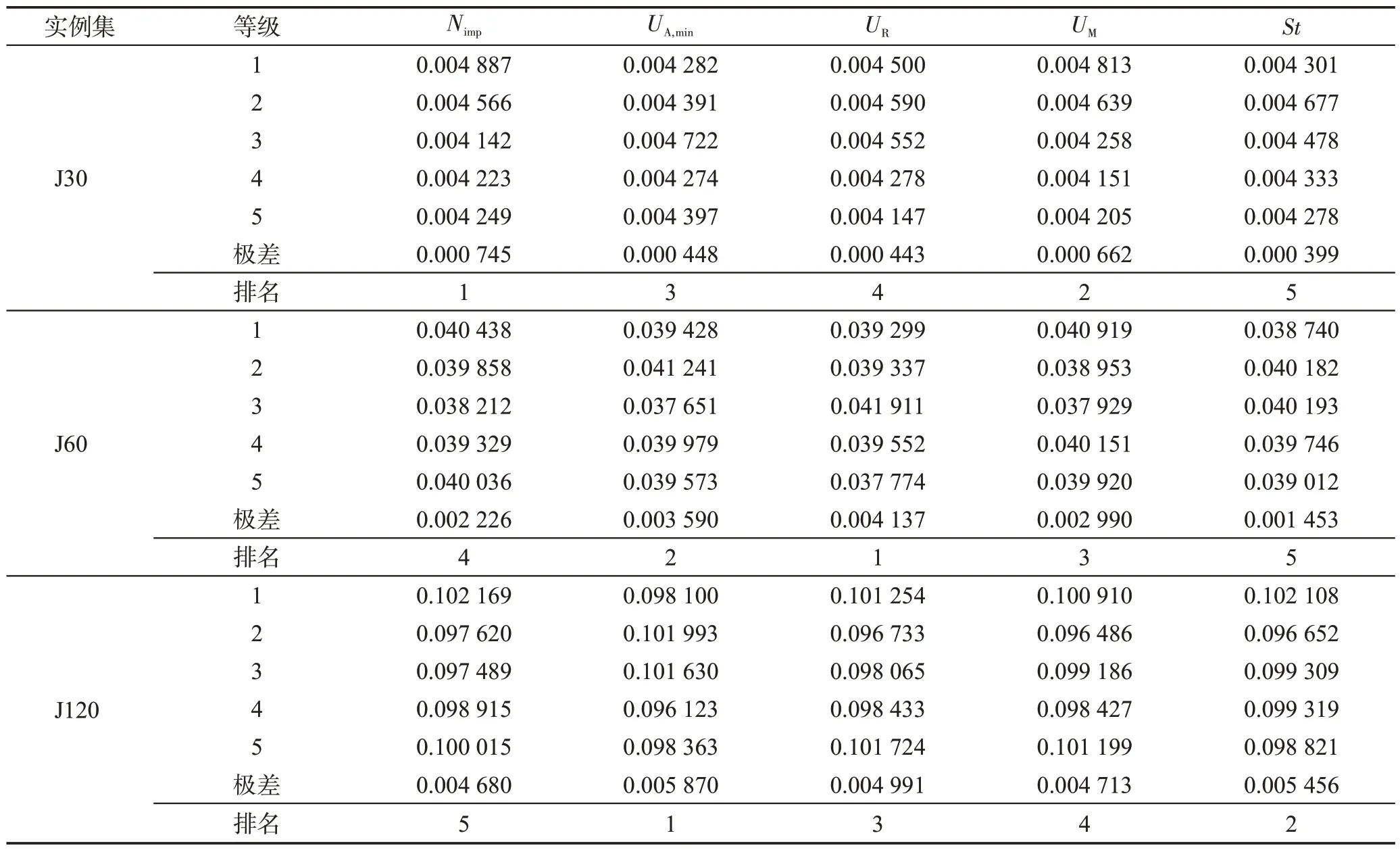
表6 均值响应表Table 6 Response table for means
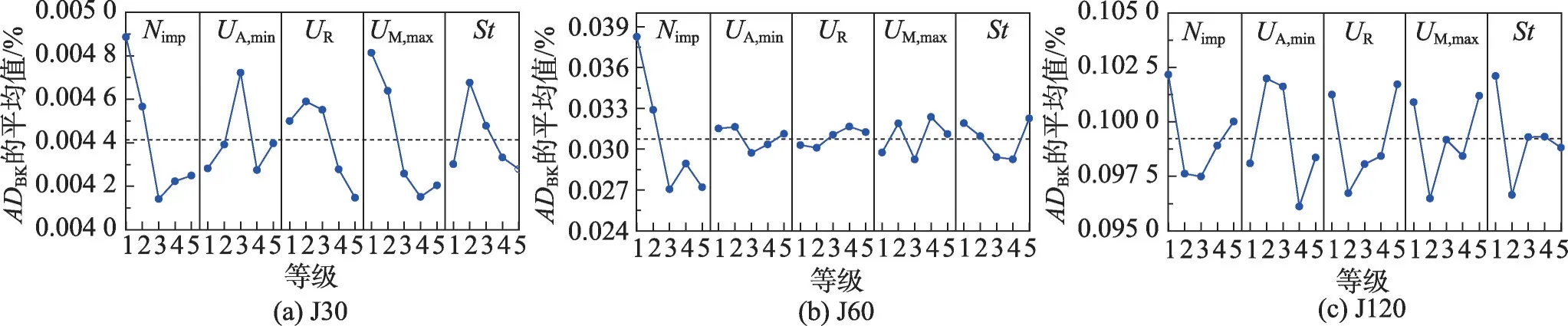
图6 TSE-ICA的参数等级变化趋势Fig.6 Factor level change trend of TSE-ICA
4.3 实验结果
表7为TSE-ICA求解3个实例集的实验结果,其中CT指每个实例的平均计算时间。图7 展示了TSE-ICA对每个实例的所求最优解的ADBK。
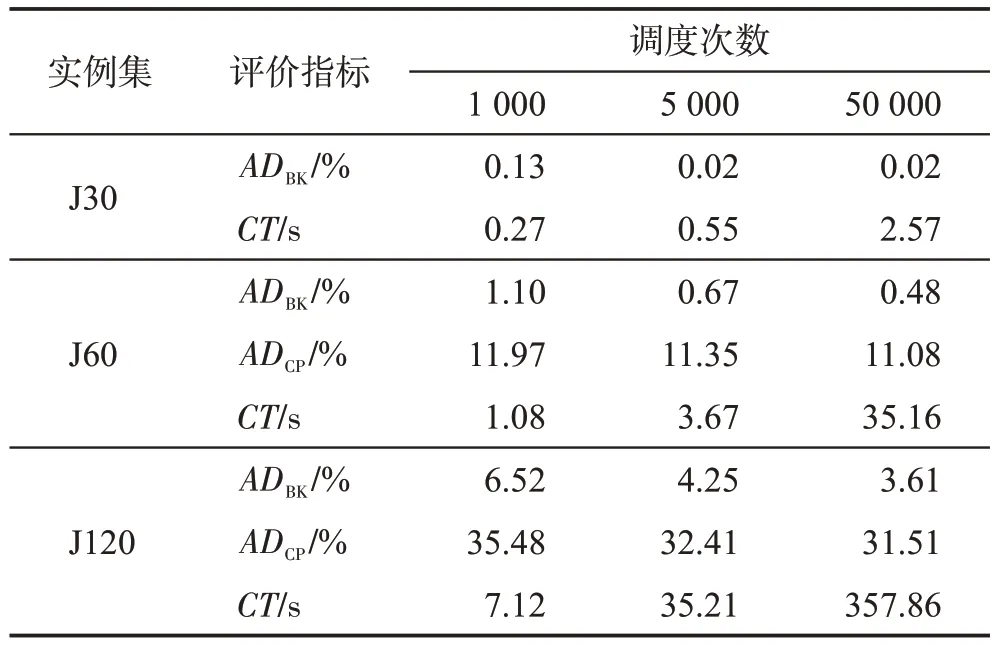
表7 TSE-ICA的实验结果Table 7 Experimental results of TSE-ICA
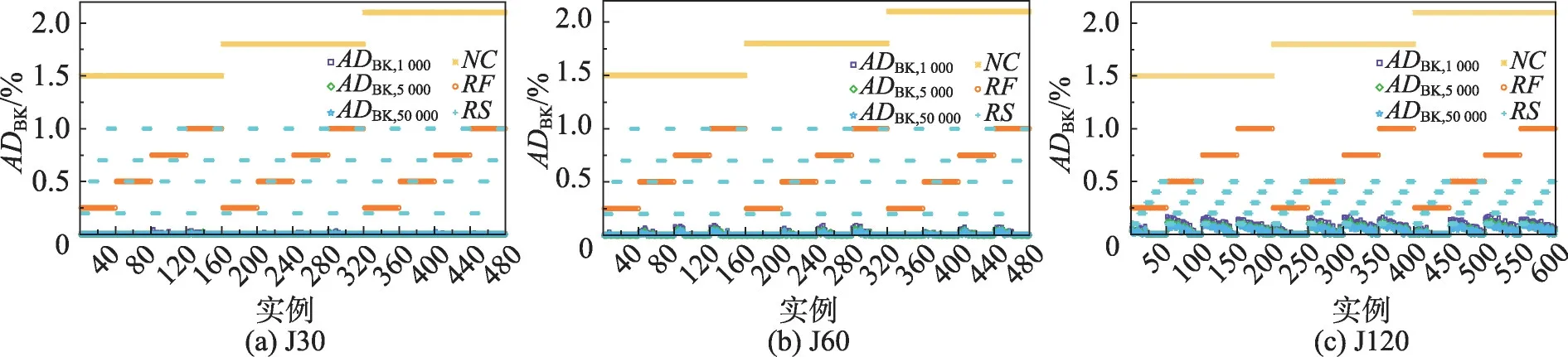
图7 TSE-ICA求解每个实例的平均偏差率ADBKFig.7 Average deviation ADBK for TSE-ICA solving each instance
如图7(a)所示,对于J30,TSE-ICA 分别能够在1 000、5 000 和50 000 次调度次数时求得444、473 和475个实例的理论最优解。其中,未能求得最优解的5个实例分别是13-6、29-1、29-5、29-8和40-1,其共同特点是RS=0.2。
根据图7(b),对于J60,TSE-ICA在3种调度次数下分别有353、367 和383 个实例的计算结果与已知最优解一致。可以发现,存在偏差的实例数量及其偏差率会随着RF的增大而增大。对于有着最小RS和最大RF的实例,算法的偏差率最大。
面对难度最大的J120,3种调度次数下TSE-ICA能够求得已知最优解的实例数分别为153、173 和181。从图7(c)中可以很明显地看出,TSE-ICA 对RF大于0.25的实例的偏差率大幅高于RF等于0.25的实例。同时,偏差率与RS呈明显的负相关。
总的来说,NC对本文所提算法的求解表现没有显著的影响。但是,实例的RF越高或RS越低,TSEICA越难对其求解。并且,随着实例所含活动数的增多,RF与RS对算法求解精度的影响越显著。
4.4 与多种先进算法的对比分析
实验结果对比共分两部分:(1)基于实验所得的ADBK和CT,TSE-ICA 与3 种同类型算法、1 种GA 改进算法和2 种DE 变种进行数值比较和分析,以验证本文算法的改进有效性和收敛效率;(2)基于国际通用标准ADCP,TSE-ICA 与11 种著名算法进行比较,进一步证明本文算法的优化性能和问题适应性。
本节列出了17 种对比算法,这些算法皆是采用或先进、或经典的优化技术构建的混合型算法。ICAS(imperialist competitive algorithm with spilt mechanism)[49]、DCCE-IICA(decimal-binary conversion and clonal evolution oriented improved imperialist competitive algorithm)[46]和ICA-DE(hybrid algorithm of differential evolution algorithm and imperialist competitive algorithm)[50]对各自应用的组合优化问题有着优异表现,IGA(improved genetic algorithm)[26]、IDE(improved differential evolution algorithm)[51]和ADDEBS(improved differential evolution parameter control and bidirectional scheduling algorithm)[29]能够较好地求解RCPSP 及其衍生问题。此6 种算法被用于第一部分的对比。其他11种算法皆遵循国际通用标准完成J30、J60和J120的测试实验,是TSE-ICA在第二部分的比较对象,这11 种算法在实验结果上都有着较强的竞争力,尤其是Search-tree+GA、ALNP 和MAOA,对J60和J120的优化效果十分出色。
4.4.1 基于当前已知最优解的算法对比分析
本小节的对比算法分别是:ICAS、DCCE-IICA、ICA-DE、ADDE-BS、IGA 和IDE。表8 统计了TSEICA 与6 种对比算法基于当前已知最优解的实验结果;表9 为TSE-ICA 与4 种对比算法(不包括ADDEBS 和IDE)的平均计算时间。ADDE-BS 和IDE 的实验数据取自现有文献。其余4 种对比算法的实验平台与数据来源同本文算法一致。
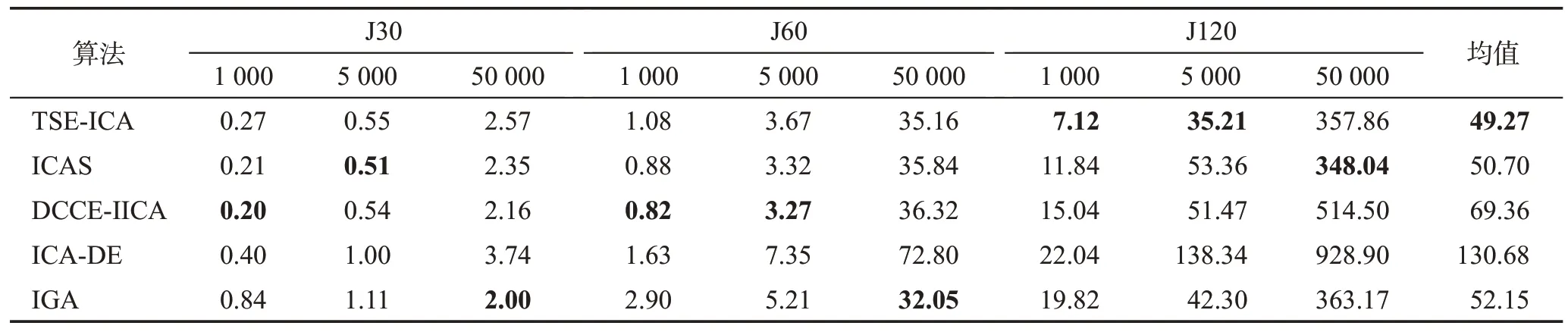
表9 5种算法求解J30、J60和J120的平均计算时间Table 9 Average computational time of 5 algorithms for solving J30,J60 and J120 单位:s
如表8所示,对于J30,IDE有着一众对比算法中最好的收敛表现,而TSE-ICA 与除IDE 之外的对比算法相比,有着很强的竞争力。并且,在4 种基于ICA 的混合型算法中,TSE-ICA 有着最好的收敛精度;对于J60和J120,TSE-ICA在最大调度次数为1 000和5 000 时的优化性能强于所有对比算法,在50 000次调度时的求解精度仅次于IGA,这意味着本文算法能够利用较少的迭代数寻得较高质量的解决方案,但随着迭代数的增多,TSE-ICA的收敛效益会逐渐不如IGA。
综合表8 的总体情况进行分析,可以发现4 种ICA变种算法对小规模实例集J30的整体优化表现不如GA 和DE 的改进算法,但面对更大规模的J60 和J120 时,4 种基于ICA 的变种算法与其他3 种对比算法相比有着不俗的优化性能。而TSE-ICA 是4 种同类型对比算法中优化精度最好的算法,这证明了本文所提改进机制的有效性。并且,对于中大规模实例集J60和J120,TSE-ICA能够在较少调度次数的约束下寻得相对最优的解决方案,初步证明本文算法有着高效的迭代寻优速率。
此外,算法运行速率是另一项重要评估指标,用于评价算法对优化问题的适用性。正如表9所示,针对实验中的3个实例集,TSE-ICA的整体计算时间最短,其次是ICAS和IGA。具体来看,对于J30和J60,除最耗时的ICA-DE外,其余所有算法的平均计算时间都较为相近;而面对J120 时,TSE-ICA 在1 000 和5 000 次调度次数时的计算耗时大幅短于其他算法,在50 000次最大调度次数的计算时间也仅与第一名的ICAS 保持着很小的差距。这证明了本文所提算法有着较好的运行速率。
为了更加确凿地证明TSE-ICA在收敛精度上的优势,本小节首先采用Friedman检验[52]对7种算法的优化表现进行排名。
表10 为置信度α为0.05 的Friedman 检验结果。基于实验得到的平均偏差率数据,表中统计了各算法相互对比得到的秩均值。因为本文的实验背景是求解最小值问题,故表现越出色的算法秩均值越小。SR是整合3 个数据集的实验结果得到的秩均值,对其升序排列可得到7 种算法的优化性能排名[53]。从表10中可以看出,对于J30,IDE和ADDE-BS这两个DE的变种算法优势最大,而本文所提TSE-ICA位于第三名;对于J60和J120,TSE-ICA的秩均值最小;SR的排名结果显示,TSE-ICA对3个标准实例集的整体表现优于所有对比算法。
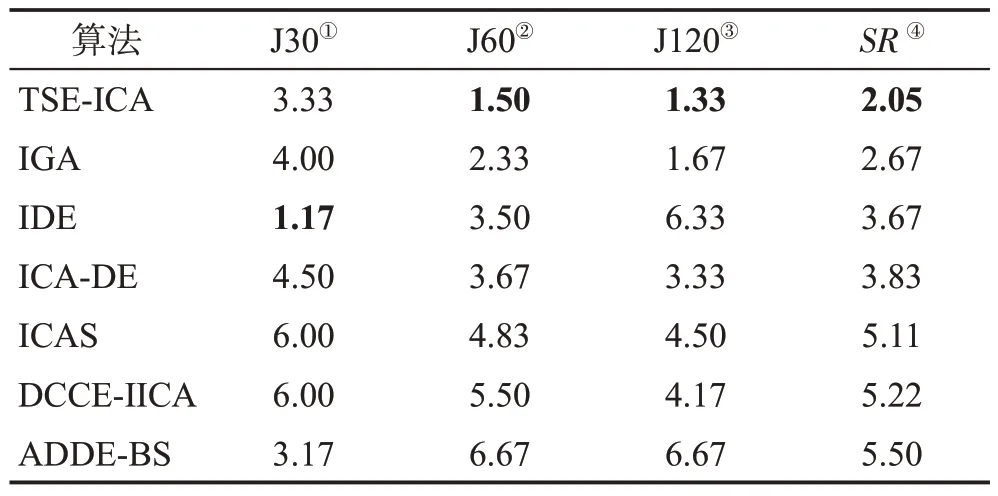
表10 7种算法的Friedman检验结果(α=0.05)Table 10 Results of Friedman test for 7 algorithms (α=0.05)
Friedman 检验能够基于实验结果确定多个对比算法之间是否存在显著性差异,但忽略了对比算法两两之间的差异性。而post hoc Iman-Davenport检验[54]能够很好地解决该问题。首先根据式(13)计算差异临界值CD(critical difference),然后将对比算法两两间的SR之差与CD进行对比,若差值大于CD,说明二者间的性能确实存在显著差异。
式中,qα是以((κ-1),(κ-1)(η-1))为自由度从F 分布统计量表得到的临界值;κ和η分别表示算法个数和实例数。
图8 为7 种算法的post hoc Iman-Davenport 检验结果。根据式(13)计算得到CD=0.162。显然,图8中TSE-ICA 与所有对比算法的SR之差皆小于CD,故可得出TSE-ICA与任意一种对比算法都有着显著的性能优势,证实了Friedman检验得出的结果。
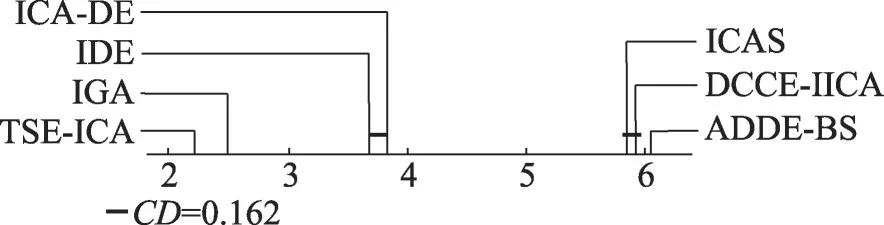
图8 7种算法的post hoc Iman-Davenport检验结果Fig.8 Results of post hoc Iman-Davenport test for 7 algorithms
4.4.2 基于关键路径值的算法对比分析
本小节与TSE-ICA对比的算法有11种,分别是:QICA(quantum-inspired genetic algorithm)[45]、EA(FBI)(a population based stochastic algorithm with forwardbackward improvement)[55]、Search-tree+GA(Searchtrees combined with genetic algorithm)[56]、ALNP(activity-list based nested partitions algorithm)[57]、MAOA(multi-agent optimization algorithm)[58]、DSA(differential search algorithm)[59]、MJPSO(multiple justification particle swarm optimization)[60]、PSO(FBI)(pseudo particle swarm optimization with forwardbackward improvement)[61]、GRASP(SS-FBI)(greedy randomized adaptive search procedure combining scatter search and forward-backward improvement)[62]、BA(FBI)(bee algorithms with forward-backward improvement)[63]和JPSO(justification particle swarm optimization)[64]。本小节所有算法的实验数据皆取自已公开发表的文献。
表11统计了12种算法基于关键路径值的平均偏差率。从表11 中可以很明显地看到:对于J30,TSEICA在调度次数较少的情况下有着最好收敛精度,但在50 000次调度时略差于MAOA、PSO(FBI)和Searchtree+GA;对于J60,本文算法的优化表现并不出色;对于J120,TSE-ICA 在1 000 次调度情况下的收敛精度相对较低,但在5 000和50 000次调度时有着最低的平均偏差率。
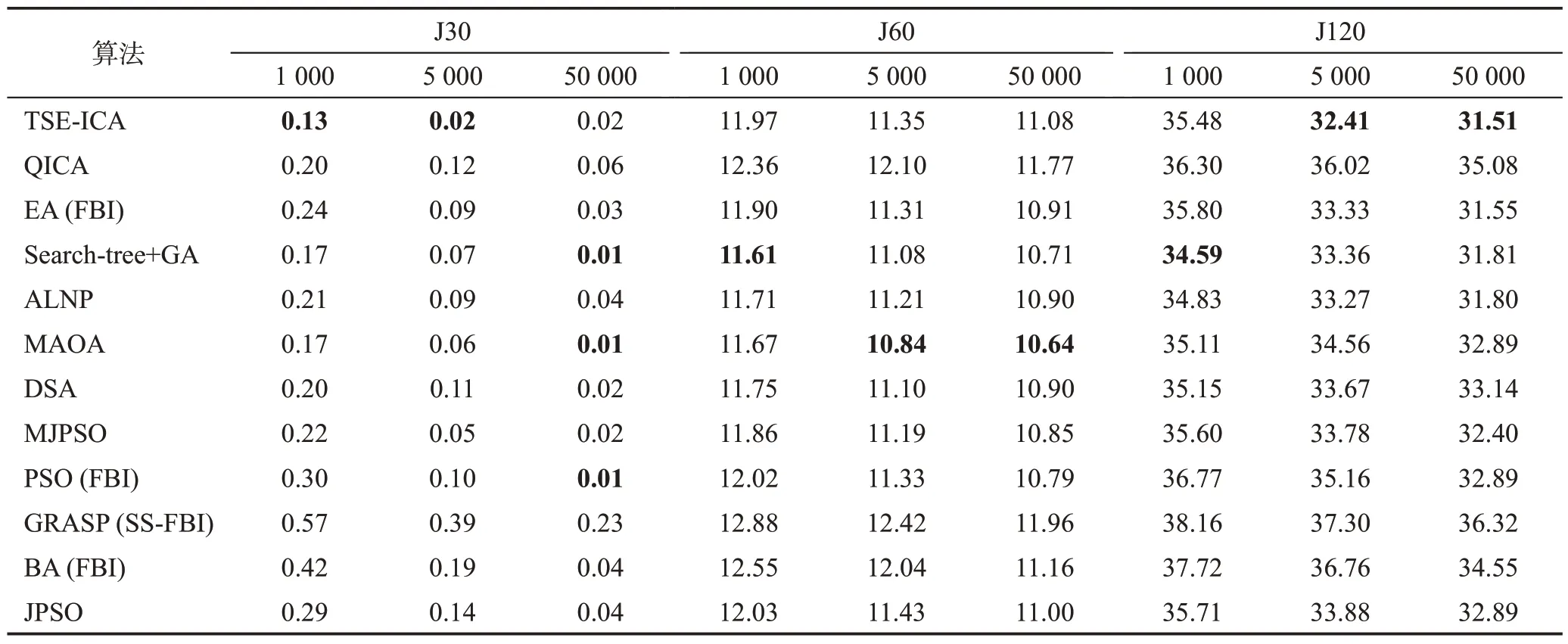
表11 12种算法基于关键路径值的平均偏差率Table 11 Average deviation of 12 algorithms based on critical-path values 单位:%
此处同样用到Friedman 检验和post hoc Iman-Davenport 检验对实验数据作进一步的分析,其检验过程同前一小节一致。表12为本小节的Friedman检验结果;图9为post hoc Iman-Davenport检验结果(根据式(13)计算得到此时CD=0.418)。
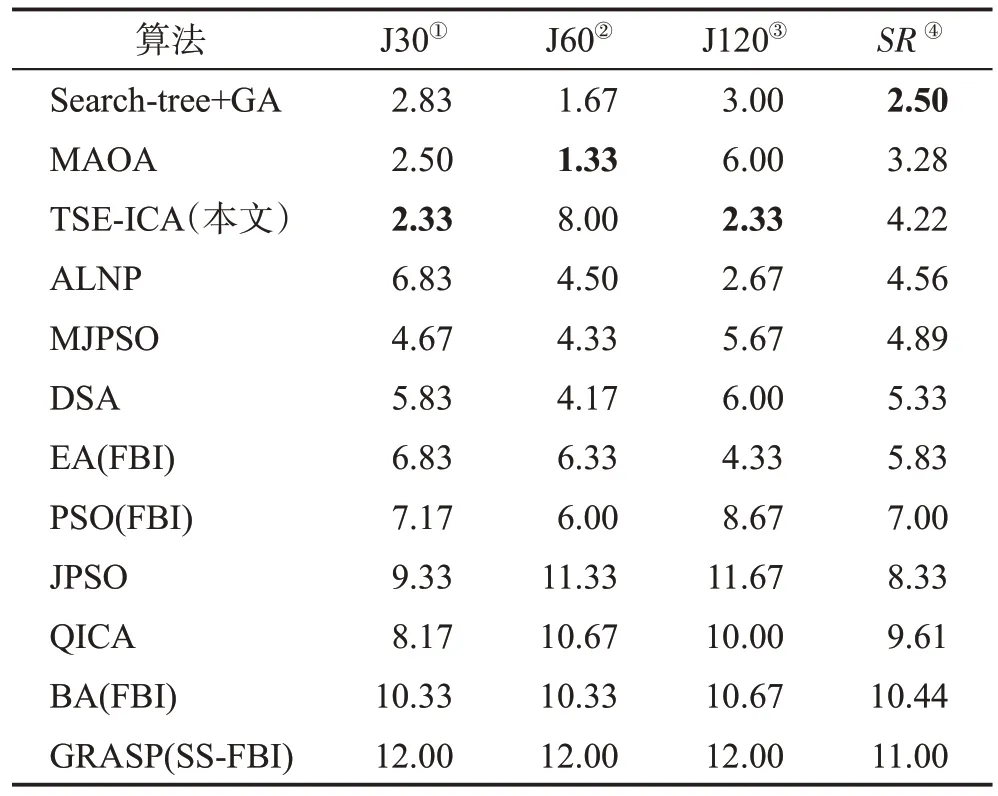
表12 12种算法的Friedman检验结果(α=0.05)Table 12 Results of Friedman test for 12 algorithms (α=0.05)
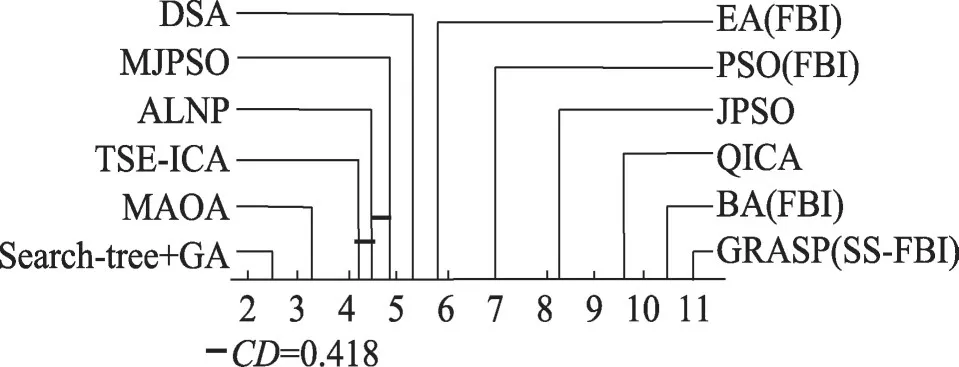
图9 12种算法的post hoc Iman-Davenport检验结果Fig.9 Results of post hoc Iman-Davenport test for 12 algorithms
如表12所示,根据Friedman检验结果,TSE-ICA对实例集J30和J120的优化表现排在了第一位,但对J60的求解能力排在了第8名。通过对SR值排序,得出本文所提TSE-ICA在众多优化算法中的性能表现排名为第3,落后于Search-tree+GA 和MAOA。从图9 可以看出,TSE-ICA 与ALNP 和MAOA 的SR之差小于CD,说明TSE-ICA与除ALNP和MAOA之外的其他算法之间确实存在显著差异,可以证明Friedman检验的结果存在合理性。
综上,可以确定本文算法与国际上的知名算法相比,在小规模数据集J30和大规模数据集J120上有着出色的优化性能和较好的适用性。对于中等规模数据集J60,TSE-ICA 虽然差于部分先进的混合型算法,但仍具有较强的竞争力。
4.5 收敛速率分析
为进一步分析本文所提TSE-ICA 的收敛速率,本文分别从3个测试集中挑选2个较难求解的实例,于图10绘制TSE-ICA与3种ICA变种(ICAS、DCCEIICA、ICA-DE)对这些实例在5 000 次调度下的收敛曲线。J30-13-5表示J30中的13-5,余同。
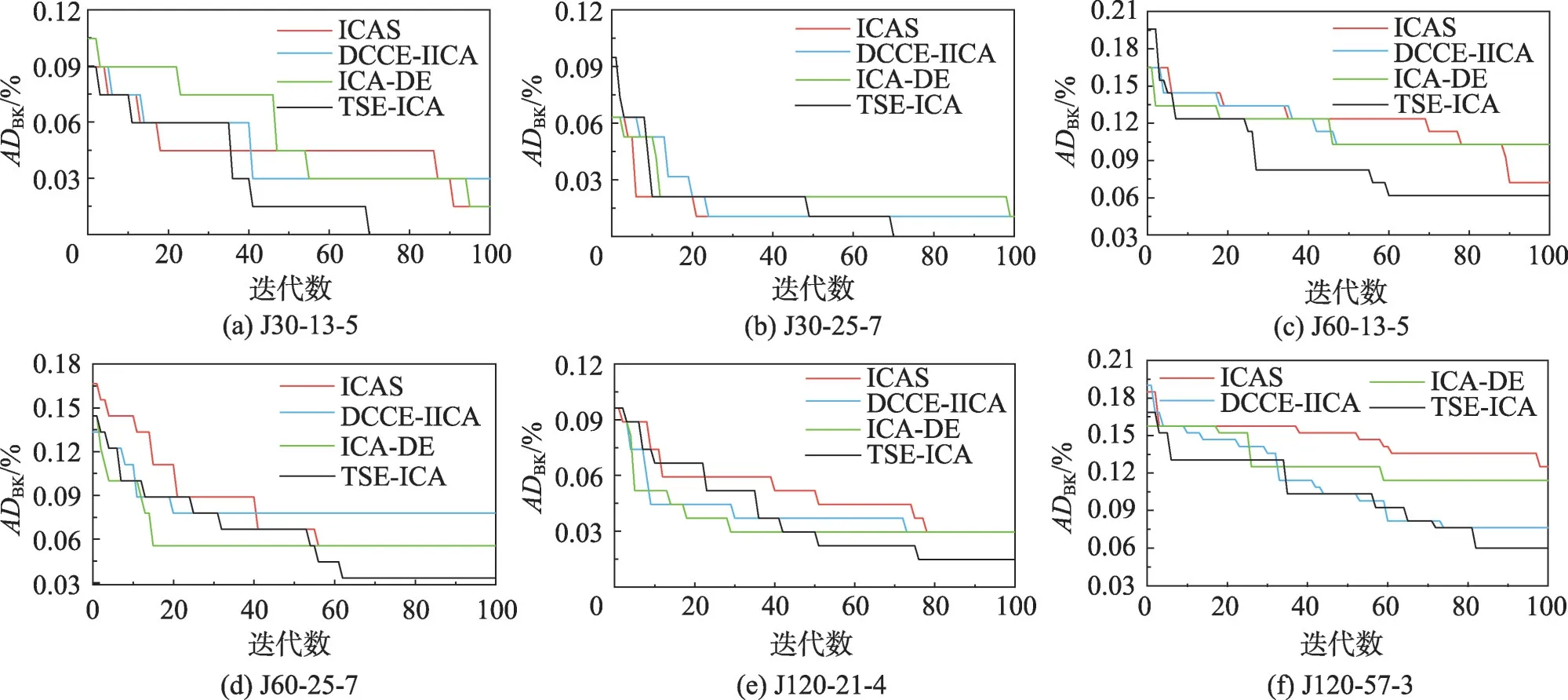
图10 4种改进ICA对6个实例的收敛曲线Fig.10 Convergence curves of 4 improved ICA for 6 instances
如图10(a)和图10(b)所示,对于J30-13-5和J30-25-7,ICAS与TSE-ICA有着最快的前期收敛速率,但仅有TSE-ICA的收敛曲线能够在中后期保持着稳定且快速的下降速率,并在最大迭代次数结束前寻得理论最优解。根据图10(c)和图10(d),TSE-ICA 对J60-13-5 有着众算法中最快的收敛速度,但在对J60-25-7 的收敛速率上慢于DCCE-IICA。在图10(e)和图10(f)中,面对J120-21-4,TSE-ICA 虽有着最好的收敛精度,但在收敛速度上不如DCCE-IICA和ICA-DE;对于J120-57-3,TSE-ICA 在前期的收敛速度优于其他算法,在中后期的收敛速率与DCCEIICA相近。
综合图10 中的所有信息,可以发现四种同类型算法都能够在演化前期有一个较快的收敛速率,但只有TSE-ICA的收敛曲线能够在中后期依旧保持稳定的下降趋势,极少发生收敛早熟的现象。这说明二阶段演化框架及其对应的搜索算子,能有效满足演化种群在不同时期的搜索性能需求,帮助算法维持稳定且高效的收敛速率。
4.6 改进策略的有效性分析
为了进一步验证组块提取策略和相同元素保留策略的改进有效性,本节对以下4 种算法进行对比:(1)采用传统同化算子的ICA1;(2)仅采用组块间同化算子的ICA2;(3)仅采用保留相同元素的组块间同化算子的ICA3;(4)采用二阶段同化算子的TSEICA。除同化算子外,这四种ICA的其余部分完全一致。图11 为4 种算法对J30-13-5、J60-25-7 和J120-57-3的收敛曲线,调度次数为5 000。从图11中可以很清晰地得出如下结论:
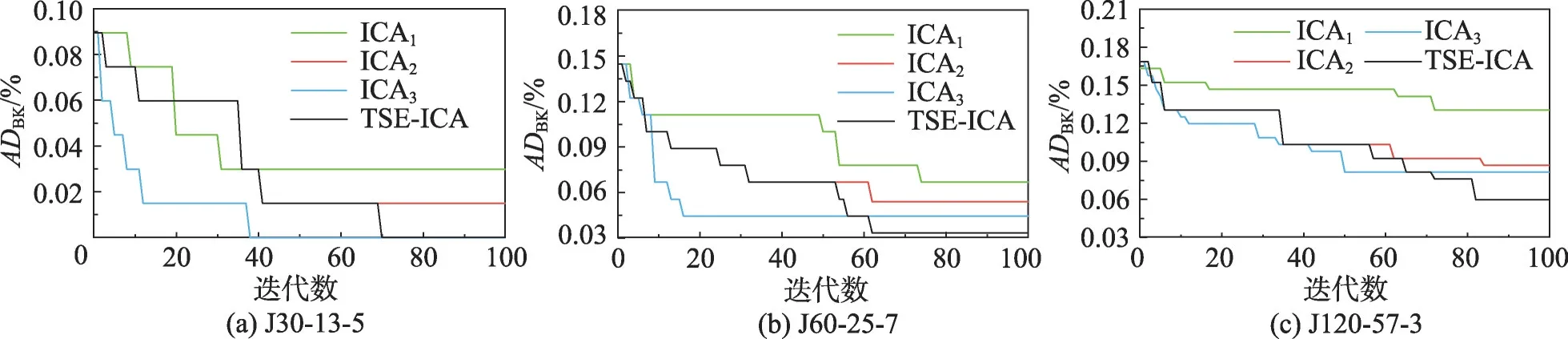
图11 4种同化算子下ICA对3个实例的收敛曲线Fig.11 Convergence curves of ICA for 3 instances with 4 different assimilation operators
(1)ICA2对3个实例的收敛精度和收敛速度明显强于ICA1,证明了利用组块提取策略改进过的同化算子具有更好的搜索效率。
(2)ICA3对3个实例的求解速率明显优于其他对比算法。并且,ICA3能够轻松求得J30-13-5的理论最优解,对其余两个实例的收敛精度仅弱于TSE-ICA。但是,除去难度最低的J30-13-5,ICA3对J60-25-7 和J120-57-3的收敛过程存在早熟的现象。这说明相同元素保留策略确实能够为组块间同化算子带来高效的收敛性能,但仅采用该种同化算子会增加算法陷入局部最优的风险。
(3)在搜索过程的前半段,ICA2与TSE-ICA的收敛曲线是重合的。但到了后半部分,TSE-ICA开始采用保留相同元素的组块间同化算子后,其收敛曲线的下降速率明显快于ICA2,且在收敛精度上超过ICA3。一方面,这进一步印证了相同元素保留策略对收敛性能的贡献;另一方面,也说明种群在第一阶段对基因多样性的积累确实有助于第二阶段的收敛,验证了二阶段演化框架的有效性。
5 结束语
本文提出了一种能够有效求解经典资源约束项目调度问题的二阶段演化帝国竞争算法。该算法基于种群多样性和收敛性能提出两种同化算子,通过二者的交替使用实现算法在不同阶段下的功能侧重。两种基于组块的邻域搜索策略用于革命机制中,加快算法收敛的同时帮助算法逃出局部最优。改进帝国竞争机制为算法提供自适应的参数决策。同时,一个记忆库不断存储迭代过程中产生的精英解,并利用其更新现有种群,保证种群的进化效率。基于标准实例集J30、J60和J120的仿真实验结果,本文算法通过与17种先进的元启发式算法进行实验结果对比,证明了本文所提改进策略的有效性、算法良好的优化性能和问题适用性。
下一步,至少还有两个需要深入讨论的研究方向:首先,本文所用的二阶段算法演化框架是一种能够平衡广度探索与深度挖掘能力的改进策略,其有望应用于其他元启发式算法的改进中;其次,实际的资源约束项目调度问题可能存在多模式、多技能、多缓冲和不确定性强等特点,如何基于帝国竞争算法或二阶段演化框架设计出有效的优化方法,是近期需要展开的下一步工作。
