纯四次孤子光纤激光器研究进展*
2023-11-16罗民张泽贤陈乃妙刘萌罗爱平徐文成罗智超
罗民 张泽贤 陈乃妙 刘萌 罗爱平 徐文成 罗智超
(华南师范大学信息光电子科技学院,广州 510631)
纯四次孤子光纤激光器是一种新型的超短脉冲激光器,能够在四阶色散和自相位调制效应平衡下保持脉冲形状稳定传输.相比于二阶色散主导下的常规孤子激光器,纯四次孤子激光器输出的锁模脉冲能量可以高出1—2 个数量级,这将为研制高能量、高峰值功率的光纤激光器提供新思路.本文系统地回顾了近年来在光纤激光器等非线性光学系统中纯四次孤子的产生以及传输特性,并探讨了纯四次孤子中已观察到的一些特殊瞬态动力学现象.同时,介绍了笔者所在课题组在该研究方向上的最新成果.最后,本文对纯四次孤子光纤激光器的应用前景以及发展趋势进行展望,为相关领域未来的研究提供有价值的参考.这些结果将有助于更全面认识纯四次孤子光纤激光器的基本物理特性.
1 引言
光孤子作为非线性系统中稳定局域结构的一种有趣现象,在光频梳[1,2]、超快激光技术[3-5]以及非线性成像[6,7]等前沿科学技术的发展中具有重要的推动作用.通常情况下,光孤子的稳定传输需要非线性效应如自相位/交叉相位调制与光纤色散相平衡[8,9].为了实验研究光孤子的形成和动力学特性,光纤激光器一直被认为是较为理想的平台.目前,光纤激光器具有高可靠性、优质光束质量、高稳定性以及易于与光纤系统兼容等性能优势,是超快激光技术未来发展的重要载体[10].在实际应用中,为了提高孤子光纤激光器的性能参数,可以通过调节多种灵活的参数来实现,如光纤色散、非线性效应、腔内增益以及损耗等.通过调控光纤谐振腔内的色散量,孤子光纤激光器可以实现不同工作状态之间的转换.在早期的研究中,孤子光纤激光器主要集中于反常色散区域[11,12].然而,输出的传统孤子脉冲能量受到孤子面积理论的限制[13,14],在峰值功率较高的情况下,孤子脉冲会发生分裂或坍塌现象,从而限制了孤子脉冲能量在皮焦量级.色散参量通常决定孤子脉冲传输过程中的压缩或展宽,对激光器的峰值功率具有极大的影响.为了避免腔内因峰值功率过高积累过多的非线性效应,Tamura 等[15]提出将腔内正、反常色散光纤交替排列的色散管理方法,以获得脉冲能量更高、脉宽更窄的色散管理孤子.受色散管理思想的引导,2006 年Chong 等[16]在腔内加入滤波器,实现在1.0 μm 波段全正色散掺镱光纤激光器,获得了稳定的耗散孤子锁模脉冲.因此,通过腔内色散调控,可以实现在传统孤子、色散管理孤子和耗散孤子之间的转化,同时,孤子脉冲能量也实现了从传统孤子的皮焦量级提升到耗散孤子的纳焦量级.
通常情况下,超快光纤激光器中超短脉冲稳定传输只需考虑非线性效应和二阶色散之间的平衡.高阶色散往往会对孤子激光器的性能产生不利影响,如导致脉冲畸变以及色散波发射等.然而,最近的实验表明,基于四阶色散主导的纯四次孤子可以实现.更为重要的是,相比传统孤子,纯四次孤子锁模脉冲能量可以提高几个数量级,这为直接产生高能量变换极限的短脉冲光纤激光器的研制提供了新的契机.实际上,高阶色散对孤子传输的影响的相关研究早已广泛开展,甚至可以追溯到20 世纪80 年代.Blow 等[17]在研究中发现,即使存在反常四阶色散的影响,短脉冲仍能够通过色散和自相位调制效应平衡而实现稳定传输,这是在不考虑光纤中增益的条件下实现的.随后,在1994年,Karlsson 和Höök [18]进一步详细研究了四阶反常色散作用下的脉冲非线性动力学过程,理论预言了四阶反常色散条件下存在类孤子脉冲,并观察到脉冲前后沿具有振荡结构.同年,Christov 等[19]通过数值模拟四阶反常色散对脉冲窄化的影响.1996年,Piché等[20]在理论上证明了孤子脉冲在四阶反常色散情况下仍具有稳定的孤子解析解.此外,2013年,Roy 和Biancalana [21]发现孤子脉冲在仅存在四阶反常色散和自相位调制效应平衡的情况下仍可以实现稳定的传输,并提出“四次孤子”的概念.四次孤子概念的提出引起了极大关注,科学家们将纯四次孤子概念与光纤激光器相结合,提出了一种新型孤子光纤激光器——纯四次孤子光纤激光器[22-24].近年来,国内外对纯四次孤子光纤激光器的研究取得了极大进展,包括传统纯四次孤子光纤激光器[23]、自相似纯四次孤子光纤激光器[25]以及耗散纯四次孤子光纤激光器[26].同时,光纤激光器实际上也是一个耗散光学系统,在二阶色散主导下的此类非线性系统中,观察到了许多有趣的孤子动力学现象,例如孤子脉动[27-30]、孤子爆炸[27,28,31-34]以及孤子碰撞[35,36]等.理论表明,高阶色散效应同样对孤子动力学具有重要影响,如三阶色散导致孤子不稳定性[37,38],四阶色散可以产生特定频率的辐射[39-41].因此,纯四次孤子光纤激光器作为一种由四阶色散主导的光纤激光器,将会产生更为奇特和复杂的动力学现象,对其研究也将进一步揭示孤子的物理本质.
本文综述了国内外关于纯四次孤子光纤激光器的最新研究进展.同时,介绍了笔者课题组在该领域的最新成果,并对未来的发展前景进行了展望.这些工作有助于优化纯四次孤子光纤激光器的性能,深入了解其物理特性,为未来的研究提供参考.笔者相信,随着技术的不断发展,纯四次孤子光纤激光器将会成为超快光纤激光技术中的重要组成部分,展现更加广阔的应用前景.
2 纯四次孤子光纤激光器研究进展
纯四次孤子是由四阶色散和自相位调制相互作用产生.为研究这种现象,需要使用具有特殊性质的材料.这种材料需要同时具有大的四阶色散、较小的二阶色散和可忽略的三阶色散特性.研究人员最初将目光聚焦在光子晶体上,但由于其存在光子带隙,使得光在其中传播变得非常困难.然而,在周期性结构中引入线性缺陷形成光子晶体波导,可以观察到孤子现象.在波导中,光与物质相互作用时会发生双光子吸收,这会导致自由载流子密度增大,进而影响波导的折射率.这相当于在波导中引入非线性诱导的自由载流子色散效应.通过色散工程的手段可以控制波导中有效折射率、群速度色散以及高阶色散,这为光子晶体波导在纯四次孤子领域的应用提供了有效的手段[42].2014年,Blanco-Redondo 等[43]通过使用色散管理光子晶体波导成功实现了皮秒脉冲的高阶孤子压缩.2016年,他们利用这种特殊设计的光子晶体波导,首次在实验上实现了由四阶反常色散主导的纯四次孤子传输[22].图1(a)展示了纯四次孤子产生的原理.负四阶色散会导致脉冲的时间展宽,但不会改变光谱形状.自相位调制则会导致光谱的展宽,但不会影响脉冲的形状.当这两种效应相互作用时,可以实现纯四次孤子的稳定传输.实验中使用的装置包括锁模激光器、光子晶体波导、可调谐延时线、超快光电二极管、马赫-曾德尔调制器以及光谱分析仪,如图1(b)所示.通过这些装置可以对在光子晶体波导传输过程中脉冲的强度和相位信息进行测量.图1(c)为扫描电子显微镜下光子晶体波导图像.此外,基于干涉技术测量的光子晶体波导色散结果也显示出这种特殊光子晶体波导具有较小的二阶正色散和大的负四阶色散特性,如图1(d)所示.

图1 纯四次孤子概念及其及实验证明[22](a) 纯四次孤子原理图;(b) 频率分辨电开关;(c) 扫描电子显微镜下的样品图像;(d) 光子晶体波导的色散测量Fig.1.Concept of pure-quartic solitons and their experimental demonstration[22]:(a) Schematic of pure-quartic solitons;(b) frequency-resolved electrical gating;(c) scanning electron microscopy image of the sample;(d) measured dispersion of the photonic crystal waveguides.
实验中将脉宽为1.3 ps,中心波长为1550 nm的高斯脉冲注入图1(b)的实验装置中,并在不同输入峰值功率下得到了实验和模拟结果,如图2 所示.图2 展示了输出的时域脉冲和频域光谱图像.在功率为0.07 W时,由于非线性效应可以忽略不计且光谱不受色散效应的影响,因此没有显著的光谱效应.在功率增大为0.7 W情况下,非线性可以平衡四阶色散并观察到基阶的纯四次孤子,测量结果(红色)与模拟(蓝色)结果一致,并且脉冲具有平坦的相位,这是孤子的基本特征[44].在较高功率2.5 W 和4.5 W 条件下,光谱会展宽并分裂成两个峰值,具有高阶孤子的光谱特征.同时,光谱发生蓝移并表现出不对称特性.此外,脉冲的相位在高功率下会出现明显的非线性时域窄化现象.在该系统中,二阶色散并不起主要作用,而由于三阶色散可以忽略不计,孤子行为完全由四阶色散和自相位调制的相互作用形成.2018年,Lo 等[45]表明纯四次孤子也可以存在于二氧化硅光子晶体光纤中.也就是说,纯四次孤子可以存在于任何具有四阶色散主导的非线性介质中.

图2 不同输入功率下的频域和时域结果(红色虚线为实验结果,蓝色实线为模拟结果)[22]Fig.2.Frequency domain and time domain results at different input powers(the red dashed line is the experimental result,and the solid blue line is the simulation result)[22].
2019年,Tam 等[46]通过数值模拟发现,纯四次孤子脉冲具有近似高斯时域剖面,并伴随着振荡尾,如图3(a)和图3(b)所示.此外,图3(c)和图3(d)线性和对数尺度上显示了相关的归一化光谱.典型特征是纯四次孤子光谱在峰值附近平缓,这是由时域振荡尾造成的.值得注意的是,纯四次孤子的时间带宽积为0.53,与传统孤子的0.32 不同.

图3 纯四次孤子输出特性(a) 线性坐标下的时域脉冲;(b) 对数坐标下的时域脉冲;(c) 线性坐标下的频域光谱;(d) 对数坐标下的频域光谱(红色为常规孤子光谱)[46]Fig.3.Output characteristics of pure-quartic solitons:(a) Time domain pulses at linear coordinates;(b) time domain pulses at logarithmic coordinates;(c) frequency domain spectrum in linear coordinates;(d) frequency domain spectrum in logarithmic coordinates(red is the spectrum of traditional soliton)[46].
2020年,Runge 等[23]进一步将纯四次孤子的概念与光纤激光器相结合,通过使用光谱脉冲整形器控制四阶反常色散,在掺铒光纤激光器内首次实现了纯四次孤子模式的运转.光谱脉冲整形器的基本单元是像素,每个像素在外加电场的作用下,其折射率可以被调控.通过将许多这样的像素排列在一起,并通过编程方式改变施加在每个像素上的电压,可以形成任意的位相掩膜.这样的装置可以实现对特定阶次色散(例如群速度色散、三阶色散和四阶色散)的补偿.图4 展示了纯四次孤子光纤激光器的原理示意图.其中,图4(a)为实验装置图.图4(b)为光谱脉冲整形器可以补偿腔内色散相反的二阶相位掩模,从而使腔内净二阶色散补偿为零.同时,光谱脉冲整形器可以提供较大的负四阶色散相位掩模,如图4(c)所示.

图4 纯四次孤子光纤激光器原理示意图(a) 实验装置图;(b) 二阶色散相位;(c)四阶色散相位[23]Fig.4.Schematic diagram of pure-quartic fiber soliton laser:(a) Experimental setup;(b) second-order dispersion phases;(c) fourthorder dispersion phases[23].
研究人员对纯四次孤子光纤激光器的输出特性进行测量.在光谱脉冲整形器不提供相位补偿时,该激光器工作在常规孤子区域,实验和理论模拟结果如图5(a)—(d)所示,光谱具有Kelly 边带[47],为典型的传统孤子.当通过脉冲整形器补偿相位并引入大量负四阶色散后,实验和理论模拟结果如图5(e)—(h)所示.与传统孤子相比,纯四次孤子频率的四次方和其阶次对应,且满足线性关系.通常情况下,孤子会以色散波的形式释放能量,这些色散波与光谱中的某些频率满足相位匹配条件从而相长干涉,从而在孤子谱中形成一个强而窄的边带.边带理论通常被用来确认净色散值[12],并为此提供理论依据.通过测量光谱边带位置,可以计算出腔内的净色散大小.在纯四次孤子中,最重要特征是能量尺度得到提升,研究人员计算纯四阶孤子脉冲能量和脉冲宽度的关系,结果表明纯四阶孤子能量与脉冲宽度的三次方成反比,因此其脉冲分裂阈值高.也就是说,在脉冲宽度足够窄的条件下,可以大幅度提升反常色散光纤激光器中脉冲峰值功率,为孤子激光器输出高能量的变换极限脉冲提供了一种全新的思路.

Fig.5.Experimental(exp.)andsimulated(sim.)spectraand time-domaincurves:(a)-(d) Conventionalsolitons;(e)-(h) pure-图5 实验和模拟上的光谱和时域曲线(a)—(d) 传统孤子;(e)—(h) 纯四次孤子[23]quartic solitons[23].
通常情况下,二阶色散主导的孤子激光器除了基于反常色散的传统孤子激光器外,还包括正色散区域的自相似孤子激光器和耗散孤子激光器.在考虑到纯四次孤子和传统孤子物理相似性的情况下,Runge 等[25]于2020 年基于分步傅里叶法研究了基于正四阶色散中的自相似演化.图6(a)展示了模拟中激光器系统结构图,包括7 m 长的无源四阶色散光纤、1 m 长的有源四阶色散光纤、可饱和吸收体、输出耦合器以及滤波器.脉冲形状和光谱如图6(b)和图6(c)所示,时域上呈三角形脉冲,频域上表现为双峰结构.可以看出,在四阶正色散作用下,脉冲向新的渐进解演化,其时域和频域曲线与二阶色散情况下有着显著差异.理论结果表明,自相似纯四次孤子脉冲在传输过程中保持形状不变,脉冲强度与时间T4/3 成正比,并且瞬时频率变化与时间T1/3 成正比,这对应于双峰光谱的产生.

图6 自相似纯四次孤子激光器(a) 模拟结构图;(b)时域曲线;(c) 频域曲线[25]Fig.6.Self-similar pure-quartic soliton laser:(a) Simulation structure diagram;(b) time domain curves;(c) frequency domain curves[25]
自相似孤子光纤激光器的脉冲演化与正四阶色散的时频特性密切相关.在受到正四阶色散下形成自相似孤子的启发后,笔者课题组在分布式正四阶色散光纤激光器模型中,利用分步傅里叶方法,发现了耗散纯四次孤子的形成[26].图7 展示了耗散纯四次孤子激光器的输出结果.其中,图7(a)为线性和对数坐标下的光谱,光谱呈现“M”型.图7(b)为脉冲强度和啁啾,与二阶色散主导下的耗散孤子时域脉冲轮廓不同,耗散纯四次孤子时域脉冲有对称基座.这是由于正四阶色散会导致脉冲在两侧的拉伸速度高于中心部分.此外,频率啁啾在中心部分几乎是线性的,在两侧会发生变化.图7(c)和图7(d)分别为1000 圈下的频域和时域演化图.

图7 耗散纯四次孤子[26](a) 线性与对数坐标下的光谱;(b) 脉冲和啁啾;(c),(d) 1000 圈下的频域和时域演化Fig.7.Dissipative pure-quartic solitons[26]:(a) Spectrum with log and linear coordinates;(b) pulse and chirp;(c),(d) evolution of frequency domain and time domain with 1000 roundtrips.
通过增大增益饱和功率,观察到了一种非对称“M”型光谱,如图8 所示.图8(a)展示了线性和对数坐标下的光谱,呈现出非对称的“M” 型.这是由于腔内能量过高导致脉冲在演化过程中积累的非线性效应增大,自相位调制和四阶正色散引起的相移不匹配所导致的结果.图8(b)显示了脉冲强度和啁啾,时域脉冲同样表现出非对称的特性.图8(c)和图8(d)展示了1000 圈下的频域和时域演化图.

图8 非对称“M”型耗散纯四次孤子[26](a) 线性与对数坐标下的光谱;(b) 脉冲(蓝色)和啁啾(红色);(c),(d) 1000 圈下的频域和时域演化Fig.8.Asymmetric “M” type dissipative pure-quartic solitons[26]:(a) Spectrum with log and linear coordinates;(b) pulse(blue) and chirp(red);(c),(d) evolution of frequency domain and time domain with 1000 roundtrips.
研究表明二阶色散以及四阶主导下的孤子可以实现在激光器的稳定传输.但是,是否可以在光纤中实现更高阶的偶次阶色散与非线性之间的匹配呢? 研究人员发现,纯高阶色散孤子同样可以实现与非线性之间的平衡,因此被命名为纯高次孤子[48].图9 展示了纯六次、纯八次和纯十次孤子的频域和时域图.其中,图9(a)—(c)为测量光谱(蓝色)和数值计算光谱(红色虚线),光谱相比图5 中纯四次孤子更加平坦.图9(d)—(f)为测量频谱图.此外,图9(g)—(i)为时域强度(蓝色)、相位(橙色)和相应的计算时域形状(红色虚线).实验结果与数值计算结果在高阶色散孤子光纤激光器中吻合良好.

图9 纯高阶色散孤子六次色散(上行)、八次色散(中行)和十次色散(下行)的频域和时域测量(a)—(c) 测量光谱(蓝色)和计算光谱(红色虚线);(d)—(f) 频谱图;(g)—(i) 时域强度(蓝色)、相位(橙色)以及相应的计算时域形状(红色虚线)[48]Fig.9.Spectralandtemporalmeasurementsof purehigh-order dispersionsolitons sextic(toprow),octic(middlerow),anddecic(bottom row) dispersion:(a)-(c) Measured(blue)andcalculated(red-dashed) spectrum;(d)-(f) spectrograms;(g)-(i)temporalintensity(blue),phase(orange),and corresponding calculated temporal shapes(red-dashed)[48].
3 瞬态动力学研究进展
孤子光纤激光器不仅能产生高性能的超短脉冲光源,还是研究非线性现象和孤子动力学的理想平台.传统孤子激光器中,研究已经揭示了光孤子在激光腔内的许多不同寻常的瞬态动力学特性,这些特性有助于深入探索孤子的本质特征.纯四次孤子属于孤子家族中的成员,很多物理性质与传统孤子相似.然而,纯四次孤子也会表现出一些特有的属性,例如脉冲振荡尾行为.这里,笔者希望从纯四次孤子独特动力学现象出发,来进一步探究孤子的本质.
2021年,Widjaja 等[49]指出纯四次孤子不具有伽利略不变性.通常情况下,自相位调制和二阶色散相互作用产生的光孤子具有伽利略不变性,因为它们的性质不依赖于群速度.然而,在四阶色散主导下的纯四次孤子中,群速度的变化必然会影响非零二阶和三阶色散,从而不符合伽利略不变性.为了验证,研究人员在数值模拟中保持设置的非线性效应参数恒定,在改变两个脉冲初始的相位差时,发现各种不同类型的碰撞动力学结果,如图10所示.

图10 纯四次孤子在不同初始相位差条件下碰撞动力学[49]Fig.10.Collision dynamics of pure-quartic solitons with different initial phase differences[49].
纯四次孤子还有一个独特的特性,即脉冲振荡尾.自相位调制和四阶色散引起的相移不完全匹配,导致纯四次孤子在时域上显示出振荡尾特性,这可能会导致能量重新分布.然而,在以二阶色散为主导的常规孤子激光器中,群速度色散与自相位调制之间实现了完美的相位抵消.这种平衡状态的实现有效抑制了孤子振荡尾的出现.2022年,笔者课题组[50]通过数值研究纯四次孤子光纤激光器中的脉动动力学现象.在稳定锁模状态条件下,通过增大系统的饱和能量,纯四次孤子将变成具有周期性振荡的状态,如图11 所示.其中图11(a)展示了纯四次孤子脉动区的时域演化,呈脉动状态并随时间偏移,周期为70 个腔往返,也称为爬行孤子状态.图11(a)中的两条最下方曲线显示了脉动纯四次孤子的中心部分(绿色)和振荡尾部(白色)的能量演化,展示了脉动过程中的能量分配过程.图11(b)则展示了频域光谱演化过程,可以观察到纯四次孤子的周期性波长偏移.

图11 纯四次孤子的脉动状态[50](a) 时域的演化(插图为纯四次孤子中心部分(绿色)和振荡尾(白色)的能量演化);(b)光谱域的演化Fig.11.Pulsation state of pure-quartic solitons[50]:(a) Evolution of the time domain(energy evolution of the pure quadruple soliton center(green) and oscillating tail(white));(b) evolution of the spectral domain.
通常情况下,倍周期分岔(脉动区)是通向混沌状态的重要途径[51].对于二阶色散主导的传统孤子,随着峰值功率的增大,在经历脉动状态后,孤子往往会进入混沌状态.然而,由于四阶色散和自相位调制引起的相移之间的不完全平衡,会导致孤子主峰和振荡尾进行能量交换,从而使纯四次孤子的振荡尾中产生的色散波部分恢复.此外,由于自组织效应,脉动孤子的振幅和轮廓会因为色散波辐射而产生周期性振荡.因此,考虑到纯四次孤子独特的时域特性,了解纯四次孤子随着峰值功率增大的脉动动力学具有重要意义.为了研究纯四次孤子光纤激光器中的脉动动力学现象,通过增大系统的饱和能量,观察纯四次孤子在稳定锁模状态下的脉冲演化.在这里,我们观察到一个不同于传统孤子的现象,纯四次孤子不会在脉动区域之后直接演化为混沌状态.相反,当饱和能量设置为较高值时,纯四次孤子光纤激光器再次变得稳定.图12(a)为纯四次孤子的峰值强度随着饱和能量增大的演化.可以看出,纯四次孤子光纤激光器在进入混沌状态之前,表现出稳定的单孤子态和脉动态之间的多重交替行为.研究结果表明,四阶色散会导致孤子的对称振荡尾产生.在不同的孤子峰值功率下,可以观察到纯四次孤子的中心部分和振荡尾部的能量再分配.图12(b)和图12(c)为多次交替过程中纯四次孤子的两个典型分布,展示了随着饱和能量的增大而发生的能量再分配,这种能量再分配导致纯四次孤子峰值功率的动态变化.纯四次孤子光纤激光器的脉动动力学表现出独特的特性,对于实际应用中的纯四次孤子激光器的设计和优化具有重要意义.
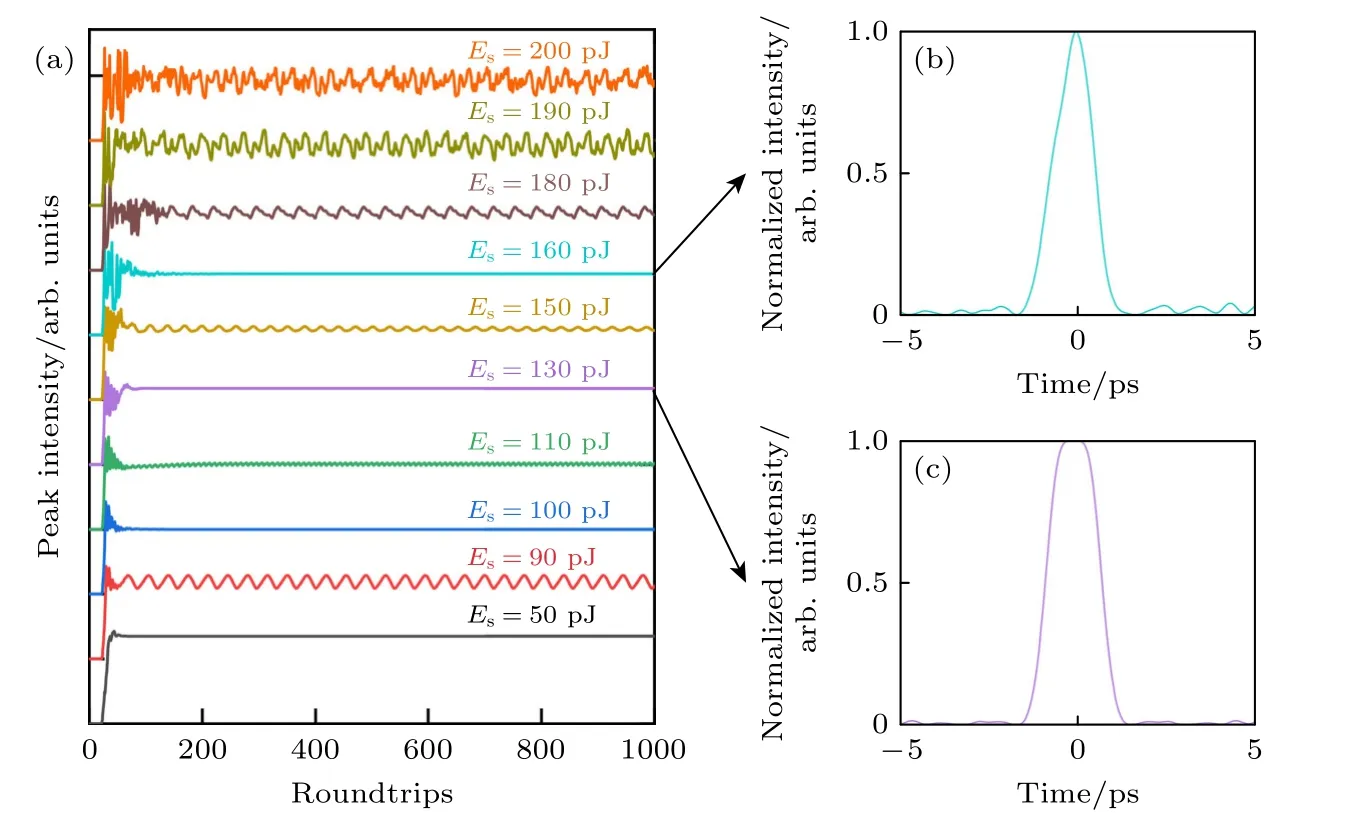
图12 (a) 具有不同饱和能量值的纯四次孤子的归一化峰值强度演化;(b),(c) 不同饱和能量下脉冲的两个典型分布[50]Fig.12.(a) Normalized peak intensity evolution of pure-quartic solitons with different saturation energy values;(b),(c) two typical pulse distributions under different saturated energies[50].
同样地,Liu 等[52]也研究了拉曼效应下的纯四次孤子,发现这种特殊的动力学现象.通过改变泵浦功率在1—6 W 区间内观察纯四次孤子的演化.结果显示,当泵浦功率低于1 W时,孤子处于稳定状态.在泵浦功率为2—4 W时,孤子会出现呼吸行为.而当泵浦功率进一步提升至6 W时,孤子仍然处于稳定状态,而不是混沌状态.这种演变过程是可逆的,结果如图13(a)所示.图13(b)为泵浦功率为1 W 和6 W 时稳定状态下的时域脉冲轮廓和相位,而图13(c)则为泵浦功率为4 W 时呼吸状态下的时域脉冲轮廓和相位.图13(d)为呼吸状态下的典型频谱.同时,图13(e)为呼吸状态下的能量演化过程,其中白色虚线表示不同段的光谱能量峰值.这些研究结果表明,纯四次孤子在不同条件下将表现出不同的动力学特性.

图13 (a) 拉曼效应下纯四次孤子的峰值功率(黑点)与泵浦功率(红色虚线)的关系(呼吸状态由灰色区域显示);(b) 稳定状态(泵浦功率为1 W,6 W)和(c) 呼吸状态(泵浦功率为4 W)的时域脉冲及其相应相位(红线);(d) 4 W 泵浦功率下拉曼纯四次孤子呼吸的典型频谱;(e) 呼吸状态谱能量演化(白色虚线表示不同段的光谱能量峰值)[52]Fig.13.(a)The relationship between peak power(black dot) and pump power(red dashed line) of Raman pure-quartic solitons(the breathing state is shown by the gray area);(b) time domain pulses in stable state(pump powers are 1 W and 6 W) and(c) breathing state(pump power is 4 W) and corresponding phases(red line);(d) typical breathing spectrum of Raman pure-quartic solitons at pump power of 4 W;(e) energy evolution of the breathing spectrum(the white dotted lines indicate the spectral energy peaks in different segments)[52].
4 结论与展望
近年来,随着应用基础研究的深入,超快光纤激光技术面临着新增的需求和挑战.纯四次孤子激光器这种新颖工作模式为超快激光器注入新的活力,吸引众多研究者的关注.本文聚焦于最近纯四次孤子光纤激光器的研究进展,总结了传统纯四次孤子、自相似纯四次孤子以及耗散纯四次孤子激光器的输出特性.同时,总结了纯四次孤子中的独特的动力学现象,有助于进一步揭示纯四次孤子的本质.在以往的理论中,四阶色散的作用通常被视为次要的色散效应,因为高阶色散可能导致孤子不稳定性和能量损失.然而,随着纯四次孤子的出现,这种观点得到了很大改变.常规孤子和纯四次孤子都属于孤子家族成员,具有很多类似的特征.但是,纯四次孤子脉冲有着最显著优点,主要体现在脉冲能量提升上.在常规孤子激光器中,能量与其脉宽成反比;也就是说,在脉冲宽度减少一半的情况下,就会提升2 倍的能量.而对于纯四次孤子激光器,能量与脉宽的三次幂成反比.这样在脉冲宽度减小一半的情况下,能量将提高8 倍.目前,纯四次孤子光纤激光器的研究仍处于起步阶段,许多有意义的工作亟待突破,如在正色散区的纯四次自相似孤子以及耗散纯四次孤子激光器的深入实验研究.需要注意的是,与反常色散区域的传统纯四次孤子激光器不同,正常色散区域的纯四次自相似孤子和耗散纯四次孤子主要依赖于四阶色散和非线性效应之间的相互作用,但其他物理效应也会发挥着重要作用,例如光纤的增益和损耗.因此,在实验中实现脉冲的稳定传输,还需要考虑参数增益和损耗作用下的新的平衡机制.此外,关于纯四次孤子激光器的瞬态动力学特性的研究仅停留在理论阶段.首先,纯四次孤子激光器不具有伽利略不变性,这为后续在纯四次孤子激光器中研究孤子碰撞动力学的多样性提供了依据.另外,纯四次孤子脉冲的振荡尾特性会导致能量的重新分配,为孤子瞬态动力学的研究提供一条新思路.我们相信,纯四次孤子光纤激光器的研究将推动超快光纤激光器输出脉冲能量和峰值功率方面的突破,并对孤子瞬态动力学基础理论和超快激光调控都具有极为重要的意义.目前,纯四次孤子激光器是一个新颖的研究领域,尚处于起步阶段,但未来有望取得进一步的发展.首先,可以通过完善色散补偿和非线性效应机制进一步压缩脉宽,实现更短的脉冲输出,从而获得更高能量和更高峰值功率.另外,实现小型化、高集成度的纯四次孤子激光器系统,为纯四次孤子激光器在医学成像、生物传感、光通信等领域的应用打开新的可能性.
