非简并双光子吸收及其应用研究进展*

吴波 王爵 王崴 周国富2)3)‡

1)(华南师范大学,华南先进光电子研究院,广东省光信息材料与技术重点实验室,彩色动态电子纸显示技术研究所,广州 510006)

2)(深圳市国华光电科技有限公司,深圳 518110)

3)(深圳市国华光电研究院,深圳 518110)

非简并双光子吸收是两个能量不同的光子同时被介质吸收,产生一次电子从基态经过一个中间虚态向激发态跃迁的非线性光学效应.非简并双光子吸收与简并双光子吸收相比,由于中间态共振效应,吸收系数得到了几十倍甚至几百倍的增大,因此在多个非线性光学应用中具有极大的潜力.本文首先介绍双光子吸收的基本原理,解释了非简并双光子吸收的增强机制;然后详细介绍双光子吸收的基本测量方法;接着综述三维半导体材料、有机荧光分子、二维材料与量子点的非简并双光子吸收相关研究;最后重点总结了其在红外探测与成像、双光子荧光显微成像、全光开关与光调制等领域的应用进展,并对领域领域的未来发展进行了展望.

1 引言

非线性光学是研究介质在强相干光场作用下的非线性光学性质变化及相关应用的一门科学.其研究开端可溯源至1961 年Franken 等[1]发现的二次谐波.伴随着高亮度、高相干光源的不断涌现,非线性光学经过60 多年的发展,已成为光学研究中的一个重要分支,在多个领域有着广泛的应用.如现代超短脉冲激光技术的发展极大依赖于非线性光学的应用,包括电-光开关、混频、倍频、光学参量放大和振荡等[2].光学相位共轭和非线性折射效应被广泛应用于光学信息处理和成像等光电器件中.此外,材料在共振和瞬态激励下的非线性光学现象也可以用来揭示材料的基本物理性质,如高激发态和载流子动力学[2].因此,材料非线性光学的研究对于传统非线性光学器件的开发、新型非线性光学器件的设计以及理解光与物质相互作用过程的物理机制具有重要的基础科学和技术意义.

双光子吸收(two photon absorption,TPA)是一种典型的三阶非线性光学效应,是由于强光入射非线性光学介质,介质同时吸收两个光子发生一次电子从基态经过一个中间虚态向激发态跃迁的光学过程.其在光开关[3]、光限幅[4,5]、生物成像[6]、微加工[7]、光信息存储[8]、光化学治疗[9]等方向均有着广泛的应用.三阶磁化率χ(3)是形成三阶非线性的主要原因.非线性吸收系数β与χ(3)的虚部有关,其关系式为Imχ(3)=c2n02ε0β/ω.其中c是光速,n0为线折射率,ε0为真空介电常数,ω是角频率.

在双光子吸收中,当两个光子的能量相同时,称为简并双光子吸收(degenerate TPA,D-TPA);反之称为非简并双光子吸收(nondegenerate TPA,ND-TPA)(图1).与D-TPA 相比,ND-TPA 的吸收系数由于中间态共振效应等影响,可以得到几十倍甚至几百倍的增大.因此,ND-TPA 在理论和实验中得到了广泛研究,在红外探测[10-15]、生物成像[16-19]、全光开关与调制[20-22]等应用中展现了巨大的潜力.

本文主要介绍非简并双光子吸收的理论原理及其近年来的研究进展与应用.首先,系统阐述了TPA 的基本物理原理,接着介绍了几种常用的TPA 系数的测量方法,然后重点回顾了传统三维半导体材料、有机荧光分子材料、新型低维材料的ND-TPA 的相关研究以及其在红外探测、生物成像及全光开关与调制方面的应用进展.最后给出了ND-TPA 研究未来的挑战及展望.

2 双光子吸收基本原理

双光子吸收是一种三阶非线性光学效应,即与P(3)相关.当频率为ω1和ω2的两束光波通过介质时,可以通过麦克斯韦方程得到稳态下的非线性波动方程:

由于频率为ω1和ω2的两个光电场沿z方向传播,两光场振幅分别为

根据非线性光学经典理论,两光场的极化强度分别表示为

χ(3)χ(3)′+iχ(3)′′为三阶非线性极化率,包含实部和虚部两部分.实部决定了其非线性折射率,即与光学Kerr 等非线性效应相关.而非线性吸收系数只与极化率虚部有关,所以在双光子吸收情况下可以直接用 iχ(3)′′代替χ(3)代入(1)式中,得到:

根据极化率对称规则:

经过简单的数学操作,可得到:

两边对z积分得到

可通过得到的耦合方程组来描述TPA 过程:

式中β1和β2为TPA 系数,

χ(3)与单光子吸收振子有着强烈的依赖关系.根据三能级简化模型,考虑简并情况的分子能级的跃迁,χ(3)可分解为D 项(D-term)和T 项(T-term)[24,25]:

其中右边第1 项为D项,第2 项为T项,µge为从基态到第一激发态的跃迁偶极矩,µge′和µee′分别对应从基态到双光子态和双光子态到第一激发态的跃迁偶极矩,Γ为对应的线宽.Δµge为基态到第一激发态的固有偶极矩之差.对于具有中心对称的材料,D 项为0.T 项为TPA 性质的决定项,与跃迁偶极矩µge、高能级跃迁偶极矩µee′和激发态能量变化相关.

对于无机直接带隙半导体,假设其能带结构为经典的抛物线模型,其双光子吸收系数则可以简化为[26,27]

Ep为凯恩能量参数,对于大部分半导体材料Ep≃21 eV[28].Eg为禁带宽度,ℏω1和ℏω2分别为入射的光子能量,n1,n2分别为能量是 ℏω1和ℏω2的入射光对应的折射率,I1,I2分别为光子能量为ℏω1和ℏω2的光束的光通量.K为常量,不依赖于材料性质,其理论值K1940 cm/(GW·eV5/2),而实验中测量值跟理论值有一定出入,但是仍然在一个量级,比如ZnS 的K值为3100—4000[29].

当入射光能量相 ℏω1=ℏω2时,为D-TPA.根据(15)式可知,D-TPA 系数只与带隙能量有关,与其三次幂成反比.因此为了提高D-TPA,需要降低带隙能量,如窄带隙半导体InSb 的D-TPA系数比宽带隙半导体ZnSe 的D-TPA 系数要大3 个数量级[30].而对于ND-TPA,除带隙对双光子吸收系数的影响外,从F2方程可以看出,当ω1或ω2减小至接近0时,F2将会大幅度增大,从而导致ND-TPA 双光子吸收系数显著提升.因此,可以通过调控 ℏω1和ℏω2的能量组合,实现ND-TPA系数的最大化,即保证 ℏω1+ℏω2＞Eg的情况下,ℏω1或ℏω2其中一个取极小值,另外一个取接近带隙值.在该极端情况下,可以近似认为能量高的光子由于能量接近于带隙能量,接近于能带间的线性吸收共振,而能量低的光子参与能带内的跃迁共振[31],因此导致ND-TPA 得到了明显增强.

3 双光子吸收测量方法

常用的TPA 系数测量方法包括非线性透射率(NLT)、Z-扫描、双光子激发荧光(TPEF)、泵浦-探测、四波混频等[32].NLT 和Z-扫描技术是直接通过测量激发光束透过样品的强度变化来获取TPA 系数.如在NLT 技术中,由于TPA 依赖于激发光强,可以通过测量不同光强下激发光束的透射率来得到样品的TPA 系数.

Z-扫描技术是利用透镜将高斯激光束会聚,然后通过调整样品在光束传播方向(z轴)上的位置,可改变其接收到激光的功率密度,测得与其位置相关的归一化透射率T(z)=P/P0,其中P和P0分别为光束通过和未通过样品的光功率.当样品从远处移至光束聚焦焦点时,其所受入射功率密度递增,因此其TPA 也逐渐增大,导致透射率递减.反之,当样品从光束焦点逐渐移至远处,其透射率递增.测量TPA 系数需要在探测器的前端保持开孔状态,以保证收集到透射的所有光子.Z-扫描技术同样可以用于测量非线性折射率.由于非线性折射率对收集孔径非常敏感,因此需保持小孔(闭孔)状态对其进行测量.

TPEF 是一种利用TPA 激发产生荧光强度测量TPA 系数的间接方法.理论上认为由于卡莎规则,所有的激发态都先弛豫到带底再发生辐射复合产生荧光.因此,无论是通过TPA 还是单光子激发,其最终发光能级、发光量子效率应该一致.其荧光强度与激发态粒子数成正比,在TPA 激发时与入射光强的平方成正比.在实际测量中,由于受荧光收集效率、光束空间或者时间分布特征、自吸收等多重因素的影响,TPEF 方法较难精确获取绝对的TPA 系数[32].当然,对于同样的光学收集装置,待测样品与参照样品的双光子吸收光谱和荧光发射光谱重合度越高,则其测量结果的可信度越高.

对于ND-TPA,通常则需要使用泵浦-探测技术测量(图2),该技术主要用于探测光电材料内部的激发态动力学.当一束较强的泵浦光激发样品以后产生基态的漂白、激发态的填充或受激辐射等物理过程,此时,另一束微弱的探测光照射到样品上,其透射或者反射受以上过程的影响会产生微弱的变化.通过光学延迟线控制泵浦光和探测光相对延迟时间,即可得到样品激发态信号随着时间的变化.在ND-TPA 的测试中,当泵浦光子和探测光子在空间和时间上重叠时,发生TPA,从而产生基态到激发态的跃迁.此时,探测光的透射率将减小,其在泵浦-探测实验中表现为激发态吸收.与一般的电子激发态吸收动力学显著不同的是,它的持续时间决定于泵浦和探测光在样品中重叠的时间.当样品足够薄的时候,它直接取决于泵浦光和探测光的脉冲宽度.

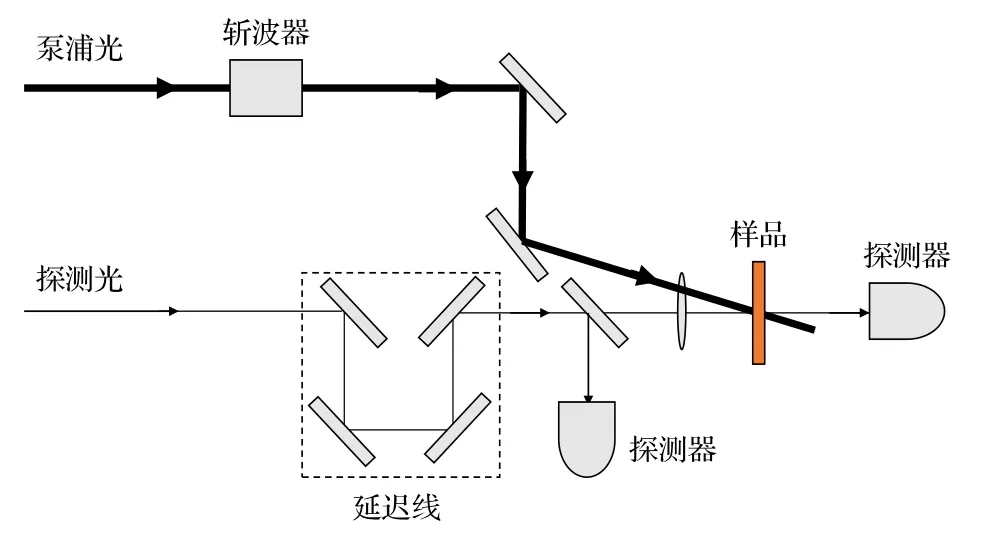
图2 泵浦-探测实验装置Fig.2.Schematics of a typical pump-probe setup.

根据Negres 等[33]提出的模型,利用泵浦-探测光谱测量的ND-TPA 的归一化透射率可以描述为

其中W=wo/wp是探测脉冲和泵浦脉冲宽度的比值,τd是泵浦和探测之间的延迟时间与泵浦脉冲宽度的比值.ρ为群速度失配参量:

其中L为样品厚度,c为光速,λp为泵浦波长,λo为探测波长,np为泵浦光折射率,no为探测光折射率.

除泵浦-探测技术以外,通过多种混频技术可以得到ND-TPA 的相关参数.TPA 系数决定于材料的三阶磁化率χ(3).χ(3)的大小与非线性相互作用的光场频率相关,一般用χ(3)(-ωs;ω1,ω2,ω3) 表示,其中ωi为相互作用的光子角频率之一,ωsω1+ω2+ω3为三阶非线性效应产生的新的光子角频率.由于相互作用及新产生光场的偏振方向可能不同,χ(3)实际上是一个四阶张量.通过光学Kerr效应、简并四波混频(DFWM)、相干反斯托克拉曼散射(CARS)等混频技术方法,可测量χ(3)(-ωs;ω1,ω2,ω3)张量,从而推知ND-TPA 的系数或截面大小[32].但是这些方法较为复杂,一般很少用于TPA 系数的测量.

4 非简并双光子吸收研究进展

20 世纪90 年代开始,随着超快激光和泵浦-探测技术的不断发展,研究人员也开始对不同材料ND-TPA 展开研究.ND-TPA 的大小不仅取决于光子对的能量和偏振,也依赖于材料的带隙、晶向、维度等重要参数.下文主要将不同材料分类为三维、低维半导体与有机荧光探针分子体系进行回顾总结.

4.1 三维半导体材料

图3(a),(b)为通过泵浦-探测手段获取NDTPA 系数的两种典型的实验数据图.X轴为探测光相对于泵浦光的延迟时间,Y轴为归一化透射率.可见,一种是归一化透射率在时间分布上类似于高斯形状;另一种是类似于梯形状,或者更准确地说是高斯分布被拦腰截去的形状.由(16)式可知,该形状特征取决于脉冲宽度、晶体的厚度及群速度色散关系(group velocity dispersion,GVD).相比于皮秒激光,飞秒激光脉冲更短,因此其泵浦光与探测光的互相干时间更短,更容易形成梯型的时间分辨探测光透射率曲线.晶体的厚度越厚,或者GVD 更加显著,泵浦光和探测光在晶体中相干时间更长,也更容易形成该形状的时间分辨探测光透射率曲线.通过(16)式拟合,能获取不同的泵浦-探测光子所对应的ND-TPA 系数.

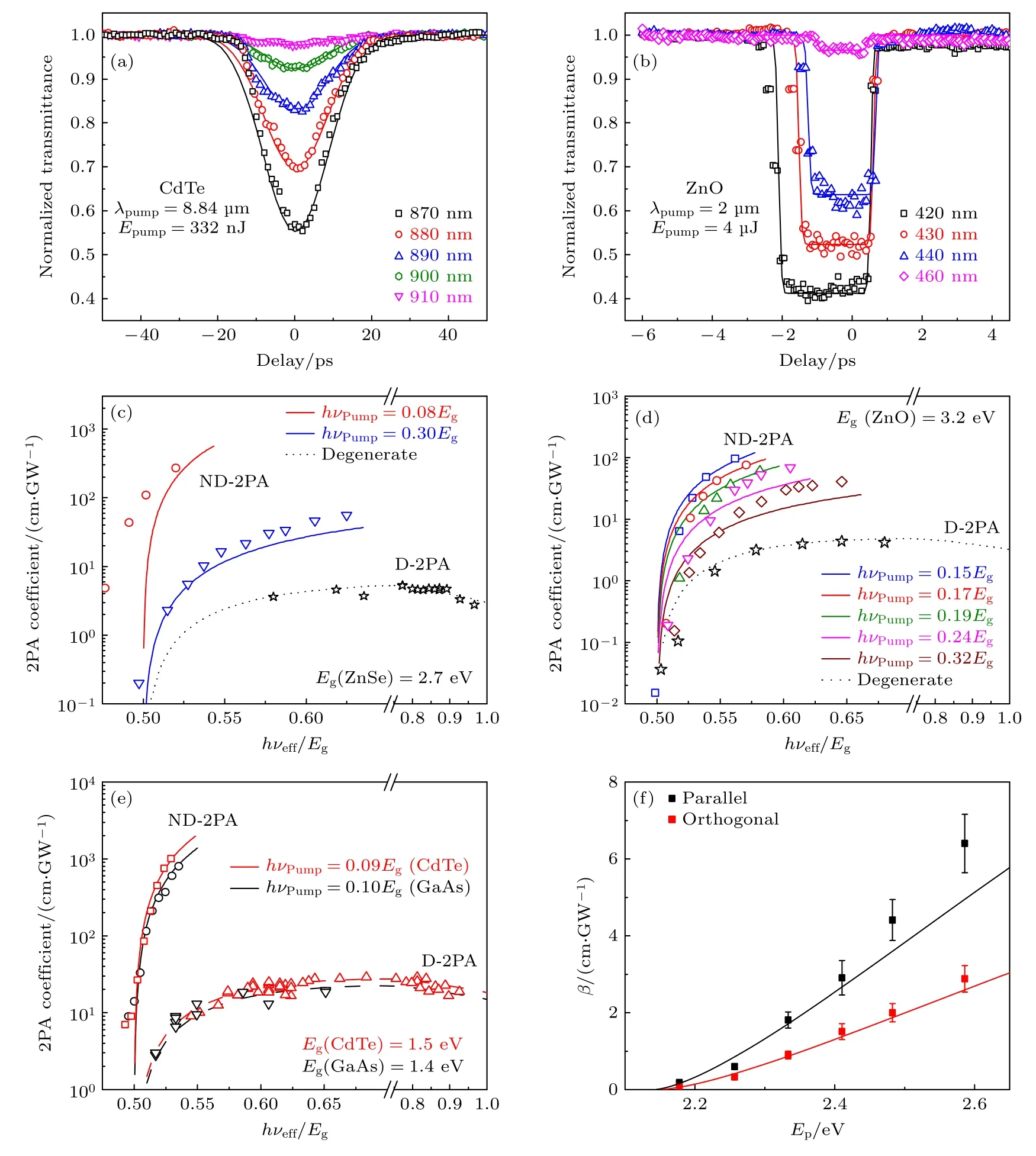
图3 典型三维半导体的ND-TPA(a) CdTe 和(b) ZnO 时间分辨归一化透射率曲线[34];(c)—(e) ZnSe,ZnO,CdTe 和GaAs 的ND-TPA 和D-TPA 系数与泵浦-探测光子的能量依赖图[34];(f) 泵浦-探测偏振方向对闪锌矿型ZnS 的ND-TPA 的影响,其中探测光偏振方向平行于z轴,泵浦偏振平行或者垂直于探测偏振方向[29]Fig.3.TheND-TPA oftypical3Dsemiconductors:Normalized transmissiondynamics of(a)CdTe and(b)ZnO singlecrystals[34];(c)-(e)ND-TPA and D-TPAcoefficientsofZnSe,ZnO,CdTe andGaAs[34];(f)pump-probepolarization-dependent ND-TPA coefficients for ZnS single crystal.The polarization of the probe beam is along the z axis,while that for the pump beam is either parallel or perpendicular to the probe polarization[29].

Stryland 团队[11,27,33-35]在ND-TPA 研究中做了大量的工作.图3(c)—(e)是该团队测得的几种典型的三维半导体材料ZnSe,ZnO,GaAs,CdTe的ND-TPA 系数与泵浦或探测光子能量的关系[34].可见ND-TPA 系数对泵浦和探测光子能量具有强烈的依赖性.当泵浦光子能量固定在非常小的区间(～0.1 eV),ND-TPA 随着泵浦光子能量接近带隙而显著增大.同样,当探测光子能量固定在接近带隙时,ND-TPA 随着泵浦光子能量的减小而剧增.这种一个光子能量接近带隙,另一个光子能量非常小的极端ND-TPA 系数相对于D-TPA 可高出2—3 个数量级.正如Wherrett[31]预测的那样,能量低的光子进行能带内跃迁共振,能量高的光子由于能量接近于带隙能量,因此接近于能带间的线性吸收共振.两次共振导致ND-2PA 得到明显的增强,趋近于单光子吸收.极端ND-TPA 使得宽禁带半导体的TPA 可接近于窄带隙半导体.如使用中红外泵浦光测量得到CdTe 最大的ND-TPA 系数约为1 cm/MW,接近于窄带隙半导体InSb 在中红外波段的D-TPA 系数[36].表1 列举了几种常见的无机半导体的D-TPA 系数βD和ND-TPA 系数βND对比.

表1 已报道的无机半导体材料的ND-TPA 系数Table 1.Reported ND-TPA coefficients for different inorganic semiconductors.

实验中,当泵浦光子能量小于带隙的1/3时,可以有效地抑制D-TPA 和三光子吸收(3PA),大幅减少自由载流子的产生从而避免额外的能量损失,使其能灵敏地检测到探测器材料带隙以下的光子能量[34].当泵浦光子能量接近带隙时,那么可以使用宽带隙半导体检测中红外光子[10-14,27,37],有效地克服窄带隙半导体效率低、背景噪声高等缺点.此外激光脉冲宽度也会影响到实验数据的采集[33,38].Bolger 等[38]发现当皮秒激光作为泵浦光时,可能会产生具有较长寿命的自由载流子,将与ND-TPA过程竞争,从而影响ND-TPA 的动力学特征.而飞秒激光具有更高的时间分辨率,可以很好地克服自由载流子对ND-TPA 过程的影响.

晶体的晶向和入射光子的偏振方向会对NDTPA 产生显著影响.Chen 等[29]研究了ND-TPA对闪锌矿型ZnS 单晶结构的依赖性.闪锌矿晶体结构具有立方对称,其χ(3)张量只有4 个独立元素不为0,分别是χiiii,χiijj,χijij,和χijji,其中下标i和j分别为晶轴[100],[010]和[001].他们将探测光的偏振方向保持与[001]晶轴一致,改变泵浦光的偏振方向,探测ZnS 的ND-TPA 系数.当泵浦和探测光偏振平行时,ND-TPA 系数是二者正交时的2—3 倍.如在480—570 nm 波段,β//为6.40—0.186 cm/GW,β⊥为2.88—0.066 cm/GW(图3(f)).另有报道GaSb的β//同样是β⊥的2—3倍,与ZnS 一致[39].Krauss-Kodytek 等[40]发现另一种闪锌矿结构材料GaAs(100)晶面ND-TPA的各向异性(β⊥/β//)高于(110)面,与Si 的相反.这种各向异性是由于闪锌矿固有的对称性造成的,它依赖于激光偏振方向与晶体偏振方向之间的几何关系,与两个独立三阶磁化张量的虚部相关[29]:

其中λp为探测波长,c为光速,ε0为自由空间的介电常数.np和ne为晶体对探测和泵浦光的折射率[29].

4.2 二维材料

二维材料是对一类特定材料的统称.它们在一个维度上的尺寸小到电子的运动受到量子限域效应的影响,而在其他两个维度尺寸较大,电子可以自由移动.典型二维材料包括纳米薄膜、超晶格、量子阱.二维材料受量子限域和介电限域效应的影响,其电子空穴(激子)束缚能较大,振子强度强.当激子态作为中间态或者最终态参与非线性跃迁时,非线性光学性质将会得到极大的增强[48,49].如前期一些关于二维材料的研究表明,其D-TPA 系数比传统三维半导体材料至少大1 个量级[50-53].

近年来,研究人员对二维材料中的ND-TPA进行研究.2018 年Cui 等[45]通过飞秒激光泵浦-探测技术同时观察到了WS2和MoS2单层膜中的D-TPA 和ND-TPA 动力学过程.瞬态透射光谱显示其在前500 fs 内会出现正负两部分信号:负信号来自于ND-TPA 产生的探测信号损耗;正信号来自于D-TPA 导致的载流子积累(图4(a)).基于二者对激发功率不同的依赖关系,可以将D-TPA 和ND-TPA 完全解耦(图4(b)).在非共振泵浦的情况下,单层WS2的D-TPA(776 nm)和ND-TPA(776 nm 和620 nm 光子对)系数分别为100 cm/GW 和250 cm/GW,并且都会随着泵浦光功率的增大而线性减小.这可归结为TPA产生的激发态电子造成的能带填充效应.在单层MoSe2中2p 激子能级的共振泵浦下,尽管NDTPA 系数同样随着功率增大而线性减小,但DTPA 系数则呈现指数衰减.当泵浦辐照度从0.6 GW/cm 升至12.5 GW/cm时,D-TPA 系数从800 cm/GW 剧降至80 cm/GW.该现象可能是能带重整化效应和能带填充效应相互作用造成的.值得注意的是,此处测得的单层二维材料中的DTPA 和ND-TPA 系数均强于传统三维半导体TPA 系数2 个数量级.

图4 典型二维材料的ND-TPA(a)单层WS2 的瞬态透射动力学曲线与功率依赖关系,激发波长 776 nm,功率0.23—2.96 mW,0 fs 之前负信号归因为ND-TPA[45];(b)单层WS2 的瞬态透射动力学曲线分解为ND-TPA 部分和D-TPA 部分贡献,黑点为原始数据,蓝点源于D-TPA,红点源于ND-TPA[45];(c) 8 nm GaAs/12 nm Al0.32Ga0.68As 量子阱的ND-TPA 系数及理论预测曲线,此处泵浦与探测偏振均为TM[44];(d)(BA)2(MA)n-1PbnX3n+1 钙钛矿薄片的超快光透射调控,泵浦波长760—980 nm,功率3.5 μW;探测波长705 nm,实线为Lorentz 拟合的调制宽度为13 fs[54]Fig.4.The ND-TPAoftypical 2Dsemiconductors:(a) Power-dependent transient transmissiondynamics of monolayer WS2,the pump wavelengthis776nm and powerin therange of0.23-2.96mW,the dip before timezero isattributed to ND-TPA[45];(b)the decoupling of transient transmission dynamics for monolayer WS2,black squares are original data,blue dots are due to D-TPA and red triangles are attributed to ND-TPA[45];(c) ND-TPA coefficients of 8 nm GaAs/12 nm Al0.32Ga0.68As quantum well as a functionofsumwavelength and its theoretical prediction,and the polarizationsofboth the pump andprobe beamsare TM[44];(d) ultrafastmodulation of light using exfoliated(BA)2(A)n-1PbnX3n+1 flakes.Pump beam:760-980 nm,power:3.5 μW.Probe beam:705 nm.Solid line is a fit using Lorentzian function and 13 fs is obtained for the ultrafast modulation[54].

2020年,Cox 等[44]利用1960 nm 泵浦,1176—1326 nm 探测研究8 nm GaAs/12 nm Al0.32Ga0.68As 量子阱的ND-TPA 特性及理论模型.当泵浦和探测光均为TM 偏振时,其ND-TPA 系数随着总波长的变化而成不连续变化(图4(c)).这可归结为轻空穴在TPA 过程中被选择性激发.他们发展了一种基于k·p方法的跃迁速率微扰计算,其理论结果很好地符合了实验数据.此外,依据该理论模型,他们预测对于红外探测波长λ2=7.5 μm,ND-TPA 系数可达5.7 cm/MW,是本项研究所采用光子对应ND-TPA系数的约360倍.

层状Ruddlesden-Popper钙钛矿是另外一种新颖的二维材料体系.其化学式通常为(LA)2(A)n-1PbnX3n+1,其中A 为尺寸较小的单价阳离子(如MA+,FA+,Cs+等),X 是卤族元素,LA 是一种长链有机阳离子,将n层角共享PbX6八面体隔离形成量子阱结构.2019年,Grinblat 等[46]利用非简并泵浦探测技术研究了机械剥离(BA)2(MA)n-1PbnX3n+1薄片的非线性光学性质.他们发现该薄片具有极强的非线性光学Kerr 效应和ND-TPA.当泵浦波长在760—980nm区间,探测波长为705 nm时,其平均非线性折射率n2≈-0.4×10-4cm2/GW,ND-TPA 系数β≈10 cm/GW.该效应可用于对可见光/近红外光谱区域实现约2%的反射率调制深度,调制时间小于20 fs,调制频率大于50 THz,这超过了已报道的基于光子超表面和单纳米天线性能的5 倍(图4(d)).

4.3 有机荧光探针分子

由于在生物荧光成像中的巨大应用前景,有机荧光探针分子的ND-TPA 性质也得到了广泛的研究.因荧光分子一般在溶液中研究,衡量其ND-TPA大小的指标通常用吸收截面σ 来表示,其单位为Göppert-Mayer单位GM(1 GM=10-50cm4·s/(photon·molecule)).σ 与吸收系数β的关系为σ1000hνβ/(NAC),其中hν为光子能量,NA为阿伏伽德罗常数,C为溶液浓度(mol/L).常用的荧光探针包括荧光蛋白和有机染料等.但是后者相比于前者在灵敏度和特异性上有着巨大的优势.在研究荧光探针的ND-TPA时,需考虑到生物样品本身的吸收散射,如水的吸收在1500 nm 附近和大于1800 nm 急剧增大.因此,选择的激发波长范围需在生物组织光学窗口范围以内,通常主要集中在近红外波段.受此局限,两个光子的能量相差不大.尽管如此,Sadegh 等[55,56]发现几种常用的探针分子,如荧光素(fluorescein)、增强绿光荧光蛋白(EGFP)、红色荧光蛋白(mKO2)、荧光素、香豆素(Coumarin 343)、罗丹明红色荧光染料(SR101)的ND-TPA 截面相对于D-TPA 截面仍然有着明显的提升,如mKO2 的最高增强可达75%.Xue等[57]通过引入多重锁相放大器,大幅提升了时间分辨和啁啾修正精度,发现罗丹明6 G(Rhodamine 6 G)的ND-TPA 截面可达 600 GM,远远高于文献[58,59]报道的D-TPA 截面(～100 GM).表2汇总了一些已报道的有机荧光分子的ND-TPA 截面及其对应的测试条件.

表2 已报道的有机荧光探针分子的ND-TPA 截面Table 2.Reported ND-TPA cross section for different organic fluorescence probe materials.

从(14)式可知,在设计有机荧光分子时,应充分考虑其基态与激发态的电偶极矩.其TPA 与分子内电荷转移(ICT)和非中心对称的偶极分子息息相关[24].如在共轭发光分子两端加上一个电子给体D 和一个电子受体A 组成D-π-A 结构能够显著增大µge,从而提升其TPA 性能[25].理论上,可以通过引入强的D/A 功能基团,增加π 共轭链长度,调控电子分布共面性以及调控其偶极矩分布实现其TPA 性能的提升[24].如2017 年Chen 等[60]在咔唑骨架上通过添加吡啶D/A 功能基团成功合成了一种咔唑衍生物荧光分子(BEMC),结合泵浦-探测和泵浦-探测荧光,通过固定泵浦波长为800 nm,改变探测波长485—650 nm 研究了其ND-TPA 激发产生的荧光强度,发现其ND-TPA 截面显著高于D-TPA 截面.如对于λ1=800 nm,λ2=650 nm光子对,其ND-TPA 截面达到了220 GM,而其等效波长的D-TPA 截面仅仅为34 GM.Elayan 和Brown[61]结合时域密度泛函理论和二能级模型比较不同结构香豆素(coumarin)衍生物的ND-TPA,发现其比D-TPA 强22%—49%,证实了其ND-TPA截面与分子的跃迁电偶极矩(μ01)有直接关联,另外所用溶剂的极性也对ND-TPA 有一定的影响.

5 基于非简并双光子吸收的应用

ND-TPA 相对于D-TPA 提高了1—2 个数量级,这种增强效应导致其可用于对红外光的计数探测.通过ND-TPA 激发荧光分子也可用于生物成像,相比于传统的D-TPA 成像具有多种优势.此外,ND-TPA 超快、超强的光响应也可以用于全光开关和调制等非线性应用,具有巨大的应用前景.本节主要从红外探测、生物成像和全光开关方面总结了ND-TPA 相关应用的前沿进展.

5.1 红外探测

传统的红外探测器是通过半导体中的线性吸收来实现探测,需要半导体带隙小于探测的光子能量,因此需使用带隙较窄的半导体作为探测器.但是半导体带隙变窄,其受到热辐射和暗电流的影响将会显著增大,导致探测器灵敏度较低[64].通常为了抑制热辐射和暗电流,需要在液氮冷却的低温环境下进行红外探测,但要接近单光子灵敏度仍具有挑战性[65,66].除了线性检测技术外,利用非线性效应也可以进行红外探测.其利用检测效率高、暗计数低、死区时间短的宽带隙半导体进行红外探测,并且在室温环境下就可以进行,这大大降低了实验成本[67,68].如利用χ(2)非线性将红外光子通过和频上转换为高能光子并被具有高量子效率的探测器探测[69-72].然而,χ(2)上转换方法需要单独的探测器和周期性极化上转换晶体来进行相位匹配.相比于和频上转换检测技术,基于ND-TPA 的红外探测非常简单,因为检测器元件本身是非线性材料,所以只需要满足吸收的两个不同波长光子的能量总和能够大于或等于半导体带隙就可以直接实现光电子检测,不需要严格的相位匹配[27].

在量子信息领域,如量子加密需要用到光通讯范围波长(1.30—1.55 μm).对该波段的红外光子计数或采样面临着诸多难题,如暗电流高、量子效率低等.2009 年Boitier 等[14]利用GaAs PMT 的NDTPA 成功对1.55 μm 红外光进行低噪声量子计数(图5(a),(b)).尽管其计数量子效率只有约10-10%,但是仍有着很大的提高空间,可以通过增大相互作用厚度、泵浦光功率、设计光学微腔或光波导等方式进一步提升其效率.2010 年Apiratikul 和Murphy[15]同样采用GaAs 光电二极管的ND-TPA(λ1=1.49 mm,λ2=1.775 mm)进行光学采样.对于脉宽约为150 fs 的激光脉冲,其时间分辨率足够实现高达4 TB/s 的光学采样.

图5 ND-TPA 用于红外光子计数与探测(a) GaAs 红外光子计数示意图[14];(b) GaAs 红外光子计数与信号光功率及泵浦强度的依赖关系[14];(c) GaN 探测器用于中红外光探测示意图[27];(d) GaN 探测器输出电压与输入红外信号光能量及泵浦功率依赖关系,信号波长5.6 μm,门脉冲390 nm[27];(e) Si-APD 红外计数速率与输入脉冲能量关系,泵浦光波长3.07 μm,能量为0.32 nJ[13];(f) MAPbBr3 单晶与Si 探头组合对1.7 μm 红外光探测[23]Fig.5.ND-TPA for infrared photon counting and detection:(a) Schematics of infrared photon counting using GaAs photodetector[14];(b) ND-TPA photon counts as a function of the signal power for different pump intensities using GaAs photodetector;(c) schematics of mid-infrared photodetection using a GaN photodiode[27];(d) output voltage of a GaN diode versus 5.6 μm input signal energy in the presence of temporally overlapped 390 nm gating pulses of various energies[27];(e) recorded count rates by the SiAPD as a function of input pulse energy,pump pulse wavelength of 3.07 μm,energy of 0.32 nJ[13];(f) 1.7 μm infrared photodetection using a combination of MAPbBr3 single crystal and Si photodiode[23].

2011 年Fishman 等[27]将极非简并双光子吸收理论应用于中红外探测中,在室温条件下,利用宽带隙GaN 光电二极管(带隙能量≈3.42 eV,对应波长为365 nm)对中红外光进行探测(图5(c)).如图5(d)所示,使用波长 390 nm、脉冲宽度为100 fs 的激光作为门脉冲(gate pulse),当泵浦光与被探测的5600 nm 中红外光在探测器上瞬时重合时,由于极强的ND-TPA,产生了光电流.通过该方法,实现了低至20 pJ 的红外脉冲能量探测.而在相同条件下,液氮冷却的HgCdTe 商用探测器的最小探测能量为200 pJ.

受其带隙限制,通用的Si 光电二极管探测器探测的波长极限约为1.1 μm.结合Si 探测器的高灵敏性和ND-TPA 的高吸收可以实现对低于Si带隙的近红外光进行探测.如2019 年Xu 等[10]以1550 nm 激光为泵浦光,利用Si-APD(雪崩光电二极管)的ND-TPA 实现了1700—1850 nm 红外光子计数.虽然足够高的泵浦功率可以使光子计数率得到显著提高,但是高强度泵浦会产生不可避免的D-2PA 甚至3PA 形成很大的背景噪声,导致探测器的灵敏度降低,限制其动态范围[27,37].2020年,Fang 等[13]利用3.07 μm 的中红外光作为泵浦光束,利用硅雪崩光电二极管成功地探测了波长为1550 nm 的信号光.由于泵浦光子能量远低于半导体禁带宽度的一半,从而消除了D-2PA 对背景噪声的影响(图5(e)).由于3PA 引起的噪声比D-2PA引起的噪声低6 个数量级,MIR 泵浦光的最大工作功率比近红外泵浦光的最大工作功率高约40 dB,从而大大提高了检测效率,其可分辨的信号功率可达到飞焦耳水平,相当于每脉冲约8 × 103个光子,与基于D-2PA 的探测相比,其计数率提高了近105倍.考虑到Si 的TPA 不够强(β＜ 2 cm/GW)[73],Wang 等[23]提出了结合MAPbBr3钙钛矿单晶的高ND-TPA 和高灵敏Si 光电二极管对近红外光探测的方案.该方法通过将MAPbBr3单晶放置于Si 光电二极管探测器前端,实现了对1 kHz 重频、1700 nm 的近红外光的高灵敏检测(图5(f)).其探测极限为1 nJ 量级,响应率约为68 V/W,优于商用热释电/热电堆红外探测器.

在利用ND-TPA 对红外光进行高灵敏低噪声探测的基础上,结合空间扫描技术可实现对物体的红外成像.2016 年Pattanaik 等[11]利用GaN 光电二极管ND-TPA 实现了对物体的近红外(1.6 μm)和中红外(4.93 μm)三维成像.其基本原理与上面的GaN 红外探测一致(图5(c)).该技术的一个特点是,其在z轴方向(深度)的空间分辨率由泵浦光和探测光的相干时间决定:

其中τFWHM是泵浦-探测互相关曲线半高宽,σ为噪声,c为光速.在该研究的实验条件下(σ≈ 2%,τFWHM≈ 350 fs),Δz≈ ± 4 μm.通过实验曲线拟合或者用更窄的激光脉冲可实现小于波长的深度空间分辨率.图6(a)—(c)展示的是利用GaN的ND-TPA 对GaAs 半导体孔状结构三维成像的结果.其中图6(a)为其形貌结构示意图,图6(b)为其ND-TPA 三维成像图,图6(c)显示的是6(b)中A,B两点对应的互相关信号.除了优越的深度空间分辨性能外,相比于商用的中红外的HgCdTe(MCT)探测器,非简并红外探测器无需液氮冷却的低温环境,这大大降低了实验成本[67,68].

图6 ND-TPA 用于中红外成像(a)用于三维红外成像的GaAs 半导体孔状结构[11];(b)基于GaN 的ND-TPA 对该结构的三维成像图[11];(c)图(b)中A、B 两点对应的泵浦探测光互相关信号[11];(d)基于硅基CCD 相机的ND-TPA 中红外振动成像系统示意图[37];(e)印有黑色字母的醋酸纤维素薄膜的中红外选择性成像.b,c,d 点分别对应的是成像激光远离振动吸收、接近振动吸收峰和与在振动吸收峰上3 种波长对应的成像效果图[37]Fig.6.ND-TPA for mid-infrared imaging:(a) GaAs semiconductor structure used for the 3D imaging[11];(b) 3D imaging of the GaAs structure using the ND-TPA of a GaN photodiode[11];(c) the cross-correlation curves of points A and B in Fig.(b)[11];(d) schematics of the vibration imaging method based on the ND-TPA of a Si CCD[37];(e) imaging a cellulose acetate film with printed letters at selected wavelengths,wavelength b:far away from the absorption of C-H vibration,c:near the absorption peak;d:at the absorption peak[37].

2020 年Knez 等[37]则结合了硅基CCD 相机的ND-TPA 与有机材料在中红外波段具有振动吸收的特点,成功实现了若干有机材料体系的中红外成像.其成像系统示意图如图6(d)所示.其中泵浦波长为低于Si 带隙的近红外光1478 nm,探测光为中红外光2750—3150 nm.后者涵盖了常见有机物的C-H 对称性和反对称性拉伸振动模式.两者组成的光子对可被Si 通过ND-TPA 探测成像.图6(e)为通过该系统对印刷在醋酸纤维素上的黑色字母的成像图.当探测光所选波长为b处时,由于醋酸纤维素在此处没有红外振动模式,红外光透射率较高,其ND-TPA 成像对比度较高.而当探测光与C-H 振动同频时(d处),红外光透射率较低,最终ND-TPA 成像对比度较差.该成像方法不依赖于相位匹配,不需要对图像进行复杂的后处理,对有机化学键的振动模式具有选择性,因而在有机聚合物或者生物成像中具有极大的应用潜力.

5.2 双光子荧光显微成像

20 世纪90 年代,随着脉冲激光器(特别是钛蓝宝石激光器)的普及,TPA 理论和应用得到了广泛研究.Denk 等[74]发明了双光子荧光显微镜,并且这种技术被共聚焦显微镜制造商迅速采用.双光子荧光显微镜与共聚焦显微镜相比,激发光和荧光的波长差更大,更容易分离,因此能获得更高的信噪比和更高对比度的图像.并且,使用红外激发光代替紫外或可见光,可以减少光损伤,具有更高的穿透深度[75,76].另外,由于对强度的二次方依赖关系,双光子激发仅局限于焦区,因此,避免了失焦激发导致的损伤.

ND-TPA 相对于D-TPA 的优势使得其很快就被应用于双光子荧光显微镜中.Xu 等[77]、Sadegh等[55,56]、Chen 等[60]证明了对于一些可用于荧光成像的分子,其ND-2PA 吸收截面远大于D-2PA,并将其归因于中间态共振增强效应[78].Lakowicz 等[79]证明了通过ND-TPA 激发的对三联苯荧光分子的荧光强度较D-TPA 情况下增强了至少1000倍,并且发现可以利用可见光或近红外光激发具有紫外波段吸收的荧光团[19,80,81].此外,与紫外激发相比,利用可见光或近红外光激发,可以显著减少对样品内部的光损伤,并增强对样品的穿透能力[82].利用各种构造的光照几何计算出ND-TPA 激发比D-TPA 激发的轴向分辨率更高[83-85].Lim 和Saloma[86]预测,与D-2PA 激发相比,ND-2PA 激发减少了由球差引起的误差.

2009年,Quentmeier 等[19]首次实现了基于NDTPA 的双色双光子荧光显微镜(2c2pLSM).通过钛蓝宝石激光器激光的800 nm 种子光和400 nm倍频光的ND-TPA 可激发带隙在紫外波段的色氨酸荧光团,从而实现了第一次测量活体的MIN-6 细胞,揭示了细胞核和细胞质的紫外荧光寿命之间的差异.2012年,Mahou 等[16]利用λ1(750—860 nm) 和λ2(1000—1300 nm)双色光的D-TPA(λ1/2,λ2/2)及ND-TPA(λ3=2/(1/λ1+1/λ2))成功地对3 种荧光团进行同时激发,实现了对果蝇胚胎“脑虹(brainbow)”标记组织的三维实时多色成像.图7(a)为该双色双光子成像原理.图7(b)对应三色荧光蛋白的双光子激发光谱.图7(c)为最终的成像效果图.类似地,2017 年Stringari 等[18]利用λ1=760 nm 和λ2=1041 nm 的两束同步脉冲激光的D-TPA 和ND-TPA 同时激发了蓝、绿、红三个荧光分子团,实现了对烟酰胺腺嘌呤二核苷酸和黄素腺嘌呤二核苷酸的同时成像.不同于基于线性吸收的传统显微成像[87],由于激发和发射光谱之间没有重叠,因此对深层组织成像具有优越性能并提高了探测效率.同年,Perillo 等[17]使用双色双光子激发(λ1=1055 nm,λ2=1240 nm)成年小鼠大脑中的血管图像进行三维重建(图7(d)).相比于D-TPA 激发,ND-TPA 激发的信号强度增加了90%,且其成像深度可以达到960 μm,优于D-TPA 激发约800 μm 的成像深度(图7(e)).

图7 ND-TPA 用于双光子荧光显微生物成像(a)常用的基于ND-TPA 的双光子生物成像的原理示意图[16];(b)由脑虹构建的mCerulean(CFP)、mEYFP、tdTomato 和/或mCherry 编码的荧光蛋白的双光子激发光谱[16];(c)小鼠皮层450 μm 厚的z 堆叠中提取的多色图像(左),不同深度(z=50,250,400 μm)的成像截面(右)[16];(d)基于双色激发(λ1=1055 nm,λ2=1240 nm)的小鼠脑部三维成像图[17];(e)小鼠脑部双色双光子激发荧光信号与深度的依赖关系,1C2P 为D-TPA 激发(λ1=1055 nm),2C2P 为双色激发(λ1=1055nm,λ2=1240nm),τ=-600fs,0fs为两种激发光的时间差[17]Fig.7.ND-TPA for two-color two-phonon fluorescence imaging:(a) A typical setup of multicolor two-photon imaging using synchronized pulses[16];(b) two-photon excitation spectra of the fluorescent proteins encoded by the Brainbow constructs mCerulean(CFP),mEYFP,tdTomato and/or mCherry,arrows indicate the excitation wavelengths[16];(c) multicolor images of a mouse cortex extracted from a 450-μm-thick z stack(left),image slices at different depth(z=50,250,400 μm)(right)[16];(d) the 3D image of a mouse brain using the two-color(λ1=1055 nm,λ2=1240 nm) two-phonon fluorescence imaging technique[17];(e) two-photon excitedfluorescence signalintensity versus tissuedepthinamouse brain.1C2P:D-TPAexcitation(λ1=1055 nm),2C2P:ND-TPA excitation(λ1=1055nm,λ2=1240 nm),τ=-600fs,0fs:the time intervals betweenthe excitationpulses[17].

5.3 全光开关与调制

光开关可以理解为在一定驱动下,通过光激发[88]或外部电流注入[89],导致光信号的某个参量从一种状态快速、可逆、不连续地转变为另一种状态的过程.对于全光开关,由于光子之间不能直接产生相互作用,因此需要光作用于非线性介质,由于泵浦光的功率高导致介质的参量发生了改变,从而实现对信号光的开关控制.在高功率泵浦光存在时,改变了介质的折射率,使信号光改变相位和输出功率,导致光开关处于开启的状态;当撤掉泵浦光时,介质参数没有改变,输出功率处在低态,导致开关处于关闭的状态.

全光开关的非线性机制可以分为单光子吸收引起的光克尔效应和双光子吸收引起的双光子折射效应.当连续光或宽脉冲光的作用下,此时主要以单光子吸收为主,光激发非线性光学介质产生大量载流子进行能级跃迁,引起光吸收和相位的变化,实现光开关开启的作用.材料的折射率的变化Δn与泵浦光的功率P成正比,即 Δn=n2(P/S)∝P,n2为材料的非线性折射系数,S为有效波导截面积.其开关速度受限于自由载流子寿命.以硅波导为例,载流子的复合时间在几百纳秒到几十皮秒之间,其与硅波导的种类有关[90].当在飞秒超短脉冲光作用下,此时主要以双光子吸收为主,材料的折射率的变化Δn与泵浦光的功率P2成正比[91].并且使用低脉冲能量的超短脉冲激光可以有效抑制自由载流子的产生,从而最大限度地减少光子的损耗[33].

2005年,Liang 等[22]将ND-TPA 应用于硅线型波导全光开关,如图8(a)所示为开关的实验装置.实验采用锁模光纤环形激光器,在1552 nm处产生1 GHz 重复频率、3.2 ps 的泵浦脉冲,并通过掺铒光纤放大器放大.连续波信号由工作在1536 nm 的可调谐激光器产生.光耦合器将泵浦光和信号光耦合到线波导中,通过ND-TPA 成功对1536 nm 连续信号光进行调制(图8(b),(c)).利用峰值功率约为1.9 W 的泵浦光,其调制深度达70%,调制时间为13 ps,但实际上受限于测量仪器的响应时间,实际调制时间应接近泵浦脉冲宽度.此后,该研究团队又报道了基于ND-TPA 的高速运行的硅波导光逻辑非门[20],如图8(d),(e)所示,将具有相同峰值功率的信号P1 和P2 组合在一起,耦合到波导中.基于ND-TPA 过程,利用P1 和P2 之和对波导输出的弱连续波探针光进行交叉调制.布尔NOR 运算以暗脉冲的形式实现.该光波导只有 1 cm,其需要的泵浦光子能量和信号光子能量之和大于硅的带隙,泵浦脉冲的波长为1545 nm 和1555 nm,信号光则为1560 nm 的连续光.该器件的逻辑运算仅需要几个pJ 的脉冲能量,开关时间小于3 ps.除NOR 门外,理论上通过硅波导的ND-TPA 也可实现低功率全光计算的NOT,NAND 和AND 门[92].

图8 (a) 用于全光开关的实验装置,EDFA:掺铒光纤放大器,OBF:光带通滤波器,PD:光电二极管,DSO:数字采样示波器[22];(b) 1552 nm 泵浦脉冲和(c) 1536 nm 处的交叉吸收调制连续波信号[22];(d) NOR 门操作原理和真值表[20];(e) P1 和P2 信号及其逻辑NOR 操作的输出信号[20]Fig.8.(a) Experimental setup of a typical all-optical switch,EDFA:erbium-doped fiber amplifier,OBF:optical bandpass filter,PD:photodiode,DSO:digital sampling oscilloscope[22];(b) pump pulses at 1552 nm and(c) cross-absorption modulated CW signal at 1536 nm[22];(d) operation principle and truth table of NOR gate[20];(e) signal P1,P2 and the output cross-modulated CW probe with logic NOR operation[20].

此外,Mehta 等[93]也演示了基于非晶硅光纤的ND-TPA 的全光开关,尽管其最短调制时间仅约为1 ps,但长寿命的自由载流子的贡献不可忽视.Li 等[94]通过波长为820 nm,功率为26.67 J/m2飞秒激光泵浦,实现了SiC 可见波段(420—720 nm)光调制,调制时间约为100—400 fs,调制深度约为10%.近年随着2D 材料的兴起,以及其相比于3D 材料更加优越的非线性光学性质,其在全光开关与调制中展现出了巨大的潜力[94].如Grinblat等[46]利 用100 nm厚的(BA)2(A)n-1PbnX3n+1薄片的光学Kerr 和ND-TPA 效应实现了可见波段反射调制,调制深度约为2%,调制时间小于20 fs.Wang 等[95]则通过少层MXene Nb2C 实现了透射光宽带调制,调制深度约2%,时间为192 fs,所需能量约为 800 nJ.

6 结论与展望

本文主要综述了ND-2PA 的基本原理、测量方法以及前沿研究进展.由于ND-2PA 较D-TPA有了几十到几百倍的增强,使得其在多种非线性光学潜在应用具有重要意义.首先,结合常用的紫外-可见-近红外探测器(GaN,Si,GaAs 等)的高灵敏度和其对可见/近红外和中红外光子对的高NDTPA,可实现高灵敏、低噪声的中红外探测,可媲美甚至优于需液氮冷却的HgCdTe 中红外探测器.但是其探测效率仍远低于紫外到近红外波段的效率.在接下来的工作,可以通过优化探测器的厚度、构建光学微腔、使用非线性效应更强的低维材料等方法来增强ND-TPA,进一步提升其工作效率.

其次,ND-2PA 应用于双光子荧光显微镜中,不仅可以保留双光子荧光显微镜的所有优点,而且可提高其分辨率,加深其成像深度,对于激发波长有更宽的选择范围以及增强了激发荧光强度,因此具有更大的应用潜力.在未来的工作中,研究的重点应该是发展设计更多的同时具有高ND-TPA 截面和发光量子产率的荧光分子、超分子结构或者量子点结构.比如在分子层面构建具有强电偶极矩的有机材料或者将适量的具有强非线性效应的低维材料嵌入荧光分子中可能是未来的研究方向之一.

对于全光开关与调制,ND-2PA 使得开关速度大于THz,并有效地降低了开关或调制所需要的能耗.但是,目前其所需的能量仍然比电学开关高几个量级.理想情况下,全光开关应该具备～fs 响应时间,开关效率为100%,开关所需功率小于1 kW/cm2,以及μm 级别的尺寸[96].显然,目前以硅为核心的光通讯系统很难达到这一要求.通过使用低维材料的强ND-TPA 和光学微腔、超表面等微纳光学尺度优化其光场分布,可能可以实现全光开关的理想目标.