拓扑材料中的平面霍尔效应*

巴佳燕 陈复洋 段后建 邓明勋 王瑞强

(华南师范大学物理学院,广东省高等学校物质结构与相互作用基础研究卓越中心,广东省量子调控工程与材料重点实验室,广州 510006)

(华南师范大学物理前沿科学研究院,粤港量子物质联合实验室,广州 510006)

平面霍尔效应(planar Hall effect,PHE)是当前凝聚态输运中研究的热点之一.近年来,平面霍尔效应,尤其是拓扑材料中的平面霍尔效应,引起了人们的广泛关注和研究,并取得了很大的进展.不同于普通霍尔效应,平面霍尔效应中的横向电流、磁场和电场可以出现在同一平面,无法用洛伦兹力解释,其很大程度上依赖于磁电阻的各向异性.本文从理论和实验两个角度介绍拓扑材料中平面霍尔效应的研究进展,深入分析了导致线性和非线性平面霍尔效应的各种外禀和内禀机制,并讨论尚待解决的相关问题和未来的发展方向.

1 引言

霍尔效应是物理学中最基本和研究最广泛的现象之一[1,2].1879年,美国物理学家埃德温·霍尔(E.H.Hall)在研究金属的导电机制时发现,当电流垂直于外磁场通过导体时,将在垂直于电流和磁场的方向上产生电势差[1,3],这种现象被称为霍尔效应.研究表明,霍尔电压与磁场强度呈线性关系,其斜率(霍尔系数)的大小和符号取决于导体中的载流子浓度和载流子类型(电子或空穴).随后,霍尔在研究磁性金属的霍尔效应时又发现了反常霍尔效应:磁性金属的霍尔电阻率包含了一个不需要外磁场且比普通霍尔效应大得多的反常贡献,它直接取决于材料的磁化强度,并且偏离与磁场的线性关系.例如,金属镍的反常霍尔系数在居里温度附近大约比普通霍尔系数大100 倍[4].1980年,德国物理学家冯·克利钦(Klaus von Klitzing)在研究二维电子气在强磁场和低温环境下的输运性质时发现分立的霍尔电导,即所谓的量子霍尔效应,其数值上等于电导量子单位e2/h的整数倍[5].后来,人们又相继发现了自旋霍尔效应[6]、分数量子霍尔效应[7]、量子反常霍尔效应[8,9]、三维量子霍尔效应[10,11]、平面霍尔效应(planar Hall effect,PHE)[12-14],以及非线性平面霍尔效应(nonlinear planar Hall effect,NPHE)[15]等.在此领域已经诞生了多个诺贝尔物理学奖.近年来,平面霍尔效应和非线性平面霍尔效应引起了人们的广泛关注和研究,并迅速取得了进展[16-18].本文将从理论和实验两个方面介绍拓扑材料中的线性和非线性平面霍尔效应研究进展,及涉及的相关物理机制.

2 平面霍尔效应

物理上,霍尔效应的出现是由于带电粒子受到洛伦兹力发生轨道偏转,而反常霍尔效应不需要洛伦兹力的作用,因而与普通霍尔效应存在本质上的不同.反常霍尔效应的物理机制直到二十世纪八十年代贝里(Berry)相位理论建立起来后才逐渐被揭示[19].事实上,反常霍尔效应与材料的电子自旋轨道耦合作用以及电子能带的拓扑性质相关.在铁磁材料中,反常霍尔效应可以由外禀和内禀机制贡献[4,20].外禀机制由晶体周期势的突然变化,如结构缺陷或杂质导致载流子的不对称散射引起[21-23],而内禀反常霍尔效应源于材料的量子力学特性,由晶体动量空间中的贝里曲率导致[24,25].从理论上说,霍尔效应和反常霍尔效应都可以归结于传导电子由于某种机制而获得一个横向的速度.在半经典理论框架下,能带电子在实空间的运动速度满足半经典运动方程[25]:,其中表示电子速度,Ωn∇k×An(k) 为贝里曲率矢量.An(k)i〈unk|∇k|unk〉代表贝里联络,描述相邻两个k点之间波函数的交叠程度.形式上,An(k)可以看作是动量空间中的“矢势”,相应地,Ωn可以看作动量空间中的“磁场”.因此,贝里曲率将贡献一个垂直于电场和“磁场”方向的反常速度项,导致内禀反常霍尔效应的出现,其霍尔电导率由反常速度项在布里渊区内的积分给出:

最近,另一种霍尔效应引起了人们的广泛关注和研究,其横向电流、磁场和电场三者共面,故称为平面霍尔效应.通常,平面霍尔效应出现在磁性材料中,如铁磁和反铁磁半导体[12,14,26,27],并伴随着大各向异性磁电阻(anisotropic magnetoresistivity,AMR)效应的出现.最近的实验发现,在强自旋轨道耦合系统中,如二维电子气体[28,29]、拓扑绝缘体[15,30]和狄拉克/外尔半金属[31-36]等非磁性材料,也能出现平面霍尔效应,掀起了研究平面霍尔效应的热潮[37-39].

2.1 三维拓扑绝缘体中的线性平面霍尔效应

2017年,Taskin 等[30]首次在非磁性三维拓扑绝缘体 Bi2-xSbxTe3中观测到了平面霍尔效应,他们的实验装置如图1(a)所示.测量的平面霍尔效应和各向异性磁电阻随电场和磁场的夹角变化满足标准的正余弦函数关系,同时,平面霍尔电阻的幅值在狄拉克点附近出现一个双峰特征结构,如图1(c)和图1(d)所示.随后,在 Sn 掺杂拓扑绝缘体 Bi1.1Sb0.9Te2中观测到了平面霍尔效应的SdH(Shubnikov-de-Haas)振荡,由此确定了三维拓扑绝缘体中的平面霍尔效应源于螺旋拓扑表面态的自旋动量锁定[40].Taskin 等理论上将观测到的平面霍尔效应归因于磁性杂质导致的各向异性电子散射,而事实上实验中并没有掺磁性杂质.因此,探索平面霍尔效应的物理机制成为大家关注的焦点.

图1 (a) Bi2-xSbxTe3 的薄膜双门霍尔棒控器件简图;(b)自旋极化杂质背散射以及背散射锁定的示意图;(c)磁场下PHE 和纵向磁电阻振幅随着角度的变化;(d)磁场下的PHE 振幅(左轴)以及有效总载流子密度(右轴)关于门电压的依赖性[30]Fig.1.(a) A sketch of the Bi2-xSbxTe3 dual-gate Hall-bar device and the measurement configuration;(b) schematic diagram of spin-polarized impurity backscattering and backscattering locking;(c) PHE and longitudinal magnetoresistance variation with angle at magnetic field;(d) dependence of PHE amplitude(left axis) and effective total carrier density(right axis) about gate voltage under magnetic field.Image cited from Ref.[30].

2.1.1 狄拉克锥倾斜机制

我们研究组发现不需要磁性杂质散射也能导致平面霍尔效应,提出拓扑表面态在面内磁场作用下的狄拉克锥倾斜与表面态自旋动量锁定是导致平面霍尔效应的根源[41].水平磁场作用下的三维拓扑绝缘体表面态可表示为

其中υF是费米速度;σ(σx,σy,σz) 为泡利矩阵;μ表示化学势;B//(Bx,By)B(cosθB,sinθB)代表外加水平磁场;动量的平方项对应于费米子的牛顿质量项,由电子-空穴不对称性引起[42].若哈密顿量不含平方项(D0),面内磁场的作用只是在动量空间平移狄拉克锥,因此不会产生任何可观测的物理效应.若D0,在平移后的狄拉克点附近,对哈密顿量作泰勒展开可得到:

其中ε0(k) 表示动量的平方项,ℏυB2DB/ℏυF.显然,面内磁场使得哈密顿量多出一项,由此导致狄拉克锥倾斜,见图2(a)和图2(b).狄拉克锥倾斜后,电子的自旋动量锁定将发生变化.如图2(c)和图2(d)所示,狄拉克锥倾斜后,等能面由圆变成椭圆,使得平行于磁场方向的态|k〉和|-k〉的自旋不再反平行,从而打开背散射通道,而垂直于磁场的方向上背散射仍被抑制.各向异性电子散射将导致磁电阻的各向异性,从而产生平面霍尔效应.

图2 (a)和(b)展现了包含动量平方项的狄拉克锥在平面磁场下发生倾斜;(c)和(d) 展示了加入面内磁场后造成的背散射锁定的解除,从而导致各向异性的纵向磁电阻率[41]Fig.2.(a) and(b) exhibit the Dirac cone containing the momentum squared term tilted under a planar magnetic field;in(c) and(d) the unlocking of the backscattering caused by the addition of an in-plane magnetic field is shown,resulting in an anisotropic longitudinal magnetoresistivity.Image cited from Ref.[41].

进一步通过格林函数形式下的久保(Kubo)公式

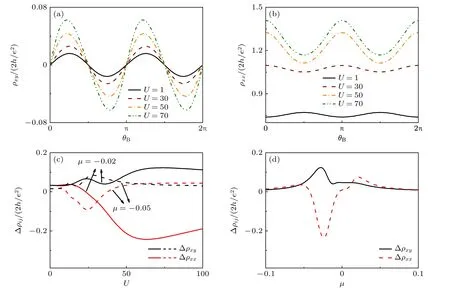
图3 (a)平面霍尔电阻(planar Hall resistivity,PHR)和(b)各向异性磁电阻(anisotropic magnetoresistivity,AMR)随着磁场与电场的角度 θB 振荡;(c) 在不同化学势下,PHR 和AMR 的振幅与杂质势U 的关系;(d) PHR 和AMR 的振幅与化学势μ 的关系(其中 U 50)[41]Fig.3.(a) Planar Hall resistivity(PHR) and(b) anisotropic magnetoresistivity(AMR) oscillate with the angle θB of the magnetic and electric fields;(c) amplitudes of PHR and AMR versus impurity potential U at different chemical potentials;(d) amplitudes of PHR and AMR versus chemical potential μ where U=50.Image cited from Ref.[41].

研究还发现,无论杂质势和化学势如何变化,PHR 的振幅不变号,然而AMR 的振幅却会随着两者变号,如图3(c)和图3(d)所示,这与文献[30]中的观测一致.该理论很好地复现了实验观测到的特征双峰结构,如图4 所示,该双峰结构对杂质势和磁场很敏感.

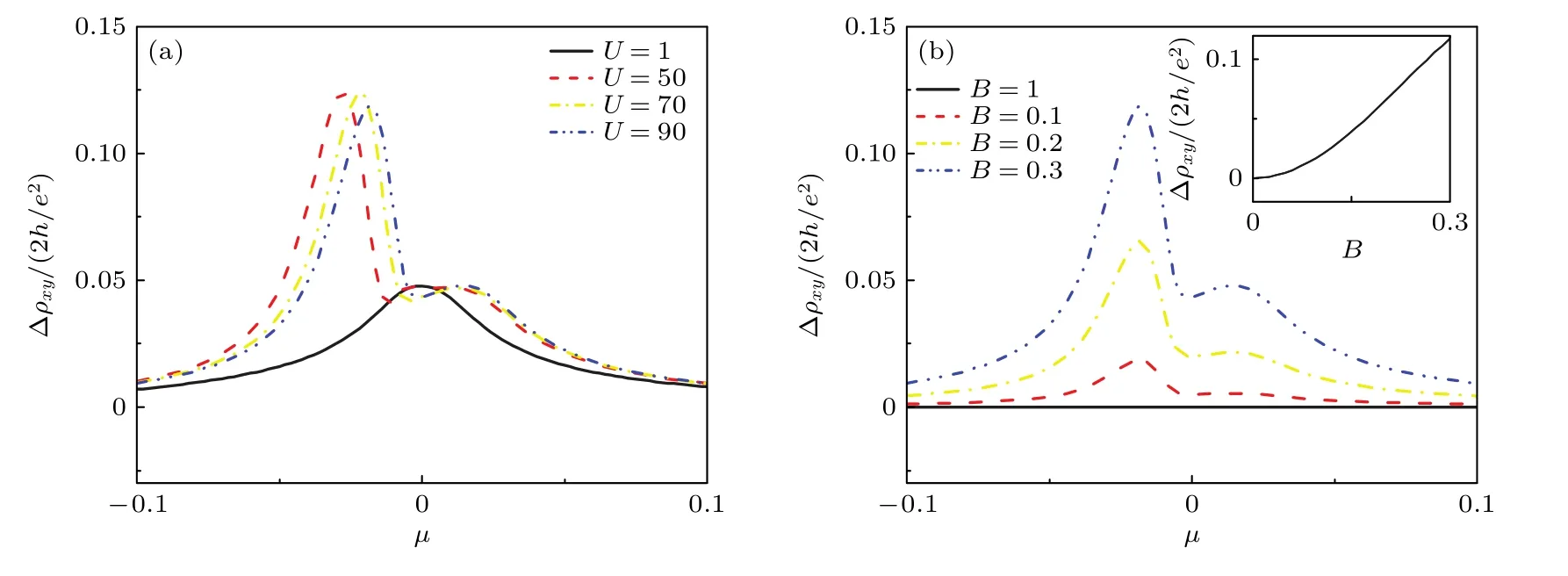
图4 平面霍尔电阻(planar Hall resistivity,PHR)随化学势的演化图(a)不同杂质势取值对双峰的影响;(b)不同磁场强度对双峰的影响.插入图展示了PHR 振幅随磁场强度B 的变化,当B 较小时呈二次方关系,较大时呈线性关系[41]Fig.4.Evolution of the double-peak structure in planar Hall resistivity(PHR) amplitude Δρxy with(a) Effect of different U values on double-peaks,and(b) effect of different magnetic field strength on double-peaks.The inset of(b) shows the Δρxy as a function of the magnetic field strength B.Image cited from Ref.[41].

2.1.2 磁振子散射机制

尽管在不同体系中平面霍尔效应的机制可能不同,但其纵向和横向电导率普遍满足(5)式和(6)式.最近在拓扑绝缘体/铁磁层中发现,平面霍尔效应在电场和磁场共线的情况下也能出现,并表现出复杂的角度依赖关系[29,38,43].如何从理论上理解这些实验结果,也是一个开放的问题.

为了解释实验观测到的复杂平面霍尔效应,我们研究组从铁磁/拓扑绝缘体异质结模型出发[16],如图5(a)所示,其哈密顿量可以写为

图5 (a)铁磁绝缘体/拓扑绝缘体双层异质结构装置以及所选坐标系示意图,其中 θB 为外磁场与x 轴的夹角.这里假设铁磁体被完全磁化(S 与B 平行).(b)各向同性费米表面上的磁振子散射示意图[16]Fig.5.(a) Schematic diagram of the ferromagnetic insulator/topological insulator bilayer heterostructure device and the chosen coordinate system,where θB is the angle between the external magnetic field and the x-axis.We assume that the ferromagnet is fully magnetized,which leads to S//B.(b) Schematic of the magnon scattering for isotropic Fermi surface.Image cited from Ref.[16].

由Kubo-Streda 公式可以得到沿电场方向(纵向)和垂直于电场方向(横向)的电导率:

其中 Δσσ//-σ⊥,θθB-θE为电场和磁场的相对夹角.这里采用缩写σ⊥≡σ⊥⊥,σ//≡σ////,其中,// 对应x˜方向,即平行于磁场的方向,⊥对应y˜方向,即垂直于磁场的方向.电导率的数值结果表明,Δσσ//-σ⊥在零温下等于零.随着温度升高,磁振子散射过程被激活,Δσ变为有限值,从而导致各向同性的线性色散下也能出现平面霍尔效应.与(5)式和(6)式比较可知,这里的(8)式和(9)式新增了后面一项,来自于非对角的霍尔效应,它们依赖于角度,最终导致复杂的角度依赖关系.此外,在翘曲效应的作用下,即λ0时,系统将会打开能隙,出现非零的贝里曲率,产生非平庸陈数,因而产生内禀的平面霍尔电导,对(9) 式中的第一项产生贡献.

2.2 外尔半金属中的线性平面霍尔效应

在过去的几年里,从有能隙的拓扑绝缘体到各种无能隙的拓扑半金属,物质的拓扑相受到了极大的关注[47-49].外尔半金属作为三维拓扑半金属的一个典型例子,在理论[33-35,50,51]和实验[52-54]方面都得到了广泛研究.外尔半金属在外尔点附近激发的外尔费米子具有线性色散关系,并且费米面包围的贝里通量在外尔点附近被量子化.外尔点可以看成具有明确手性的拓扑电荷,并且在动量空间充当贝里曲率的源或汇[55].

理论预言不久[56,57],外尔半金属态在TaAs[58,59]以及几种不同的化合物[60-62]中被实验所证实.它们独特的拓扑性质赋予了外尔半金属态许多有趣的物理特性,其中,手征反常和手征磁效应最为突出.在拓扑场论框架下,若配对的外尔点在能量-动量空间沿四维轴矢量(b0,b) 分离,则可以在外尔半金属中观察到手征反常和手征磁效应.虽然四维轴矢量没有打破系统的手征对称性,但它打破了体系的洛伦兹对称性[63].因此,通过局域手征变换消除四维轴矢量后,将会在路径积分测度中引入一个类Chern-Siomons 项[63,64],由此导致反常电磁响应(b0B+b×E).由规范不变性,可以推导出连续性方程

图6 (a)在磁场B 存在下,左手性和右手性费米子填充的能谱;(b) 存在额外平行于磁场B 的电场E 时左手性和右手性费米子的能谱填充图[65]Fig.6.(a) Energy spectra of left-handed and right-handed fermions in the presence of a magnetic field B;(b) energy spectra of left-handed and right-handed fermions in the presence of an electric field E additionally parallel to the magnetic field B.Image cited from Ref.[65].

2.2.1 (类)手征反常机制

一般情况下,单手性外尔点附近的低能有效哈密顿量可以表示为

其中χ±1 表示外尔费米子的手征荷,常数C是倾斜因子.在弱磁场下,朗道量子化可以忽略,电子输运可以用半经典玻尔兹曼方程描述:

其中,fk是电子的分布函数,ℏk是准动量,Icoll{fk}是碰撞积分.通过解r和k满足的半经典运动方程可得:

其中,vk∂εk/∂k为电子的群速度.这里,除了洛伦兹力的贡献,动量空间下的反常速度出现了E·B项,并且与贝里曲率绑定.实际上,这一项对应了手征反常的贡献.

在弛豫时间近似下,考虑洛伦兹力的影响,将(13)式代入电流密度公式,可求得体系的电导率表达式[31]:

图7 (a)平面霍尔效应测量装置示意图;(b)平面霍尔电导率振幅随磁场强度B 的变化(其中插入图为纵向电导率);(c),(d)B 5 T时纵向磁电导率和平面霍尔电导率随角度 θ 的变化[31]Fig.7.(a) Schematic diagram of the planar Hall effect measurement device;(b) amplitude of planar Hall conductivity as a function of magnetic field(the inset is the longitudinal conductivity);(c),(d) variation of longitudinal magnetoconductivity and planar Hall conductivity with angle θ for B 5 T.Image cited from Ref.[31].

我们研究组发现,若外尔半金属存在电子-空穴不对称tk2,手征化学势除了手征反常的拓扑项贡献,还包含非拓扑的贡献[70].考虑外尔半金属的电子-空穴不对称后,不加磁场时,外尔锥不倾斜,如图8(a) 所示.随着外磁场的加入,两个外尔锥将沿着磁场向相反方向移动并倾斜,见图8(b).此时,两个费米子口袋中电子的填充形式是相互对称的,因此具有相同高度的费米面.然而,在电场的作用下,这种对称性会被破坏,导致不同手性外尔锥的费米面不再对齐,从而产生手征化学势.因此,即使没有手征反常效应,也可能在两个外尔谷之间建立非零手征化学势,如图8(d)所示.在弱磁场和零温近似下,应用玻尔兹曼方程可以获得手征化学势如下:

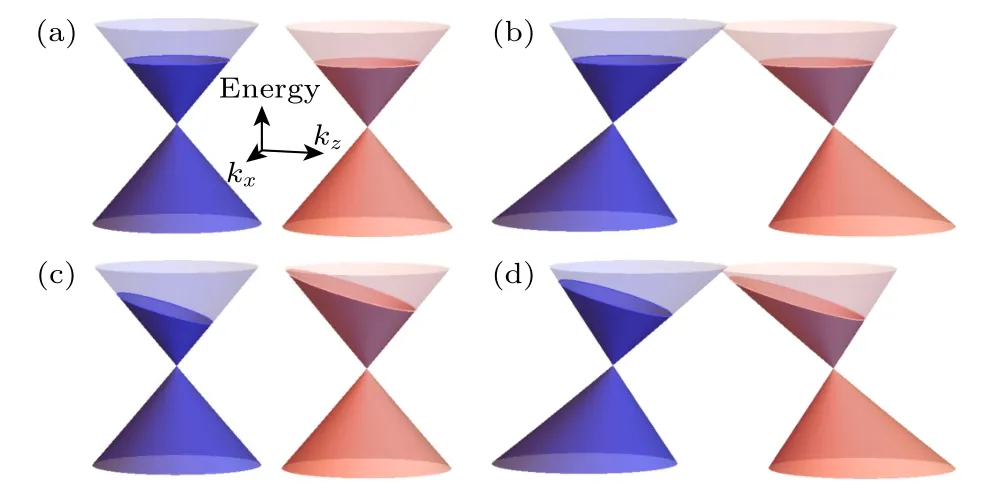
图8 塞曼场不存在[(a),(c)]和存在[(b),(d)]时的Weyl锥和费米子填充,第一行和第二行分别为 E 0和E0.我们注意两个锥之间的手征化学势可以分别由(c)手征反常,或是(d)倾斜效应产生[70]Fig.8.Weyl cone and fermion filling in the absence [(a),(c)] and presence [(b),(d)] of the Seeman field with E 0 and E0 in the first and second rows,respectively.We note that the chiral chemical potential between the two Weyl cones can be generated by(c) the chiral anomaly,or(d) the tilt effect,respectively.Image cited from Ref.[70].

其中τinter(τintra)代表谷间(谷内)弛豫时间,α2tgµBB/(ℏυF)2,kFEF/(ℏυF) 为费米波矢,EF表示费米能.由(16)式可以看到,外尔锥的倾斜效应不仅会抑制手征反常,还会产生一个正比于倾斜参数和磁场的额外类手征化学势.此外,这里的贝里曲率Ωχ-χk/(2|k|3) 与倾斜因子完全无关,这意味着倾斜机制并不会影响手征反常的拓扑性质,也就是说它所导致的类手征化学势可以是非拓扑的.

计算的纵向磁电导率和平面霍尔电导率分解成三部分[70]:ΔσizσDδiz+其中σD为Drude 电导,

ne(1/3π2) Δne(α)-δizne代表磁场修正后的载流子浓度.当t0时,手征反常(B) 项满足标准的角度依赖关系[31],而外尔锥倾斜项为零.有限t下,手征反常项会被抑制,导致 Δσiz(B) 表现出复杂的角度依赖.此外,(18)式第二项来自于反常速度与倾斜效应的共同作用,若α与磁场无关,将导致正比于磁场强度B和倾斜参数t的磁电导率[50,51,71].

3 非线性平面霍尔效应

非线性效应的早期研究主要是探讨半导体的非线性光学现象[72].近年来,随着拓扑量子材料的大量涌现,拓扑材料中的非线性效应(即电流对外部电场的二阶响应J ∝E2)也引起了人们的关注.在Sodemann 和Fu[73]提出非线性霍尔效应的概念后,人们在其理论和实验方面的研究中均取得了很大的进展[74-77].在非线性霍尔效应的实验装置中,如图9所示,如果施加面内磁场,且固定外加电场的方向(沿着x方向),通过在y方向和x方向测量电压、电阻,便可以分别讨论非线性平面霍尔效应和非线性磁电阻效应[15,78-83].此外,旋转面内磁场的方向,还可以得到电压、电阻(或电流)与磁场角度的依赖关系.在对非线性磁电阻效应的深入研究中,人们发现,各向异性的非线性磁电阻可以被用来预测霍尔电压的产生.基于实验上的重要进展,非线性平面霍尔效应引起了国内外学者的广泛关注.最近,Yasuda 等[83]在非磁性双层拓扑绝缘体中观察到了非线性霍尔效应,该效应被认为是由磁振子的不对称散射导致的.随后,He 等[15]在非磁性拓扑绝缘体Bi2Se3中也观察到了非线性平面霍尔效应,其物理机制被归结为自旋电流与电荷电流的转换,且该转换是在自旋动量锁定和时间反演对称破缺的共同作用下发生的.实验上的发现推动了理论方面的研究.为更好地解释非线性平面霍尔效应的起源,人们相继提出了诸多微观物理机制.对非线性平面霍尔效应的研究开辟了一个新的研究课题,即利用磁场来控制霍尔电压,这也为电子器件的多样化发展提供了一个新的路径.

图9 非线性平面霍尔效应和非线性磁电阻的测量示意图[15]Fig.9.Schematic illustration of the simultaneous measurements of nonlinear planar Hall effect and nonlinear magnetoresistance.Image cited from Ref.[15].

图10 (a)电场作用于三维拓扑绝缘体上,横向产生电场E 的二阶非线性自旋电流 ;(b)外加磁场 B//E,横向非线性自旋电流部分转换为电荷电流 Jy(E2),产生非线性霍尔效应[15]Fig.10.(a) When an electric field E is applied to three dimensional(3D) topological insulators,a transverse nonlinear spin current at the second order of E is generated;(b) when an external magnetic field B//E,the transverse nonlinear spin current is partially converted into a charge current Jy(E2),giving rise to the nonlinear Hall effect.Image cited from Ref.[15].

最近,Rakhmilevich 等[43]在铁磁绝缘体/拓扑绝缘体异质结上观察到非常规的平面霍尔效应,即当面内的磁场平行于电流时,平面霍尔效应信号显著,而在磁场垂直于电流时,平面霍尔效应反而受到抑制,这与以前观察到的平面霍尔效应完全不同.在排除线性平面霍尔效应的机制解释后,人们将目标转向非线性平面霍尔效应.为了更好地解释非线性平面霍尔效应的起源,人们提出了各种微观物理机制.He 等[15]在非磁性拓扑绝缘体Bi2Se3薄膜实验中发现了非线性平面霍尔效应,其非线性霍尔电阻与外加电场和磁场成线性关系.该现象的物理机制被总结为:在引入翘曲项或电子-空穴不对称的质量项后,在自旋动量锁定和时间反演破缺的作用下,非线性的横向自旋电流可以转换为电荷电流,由此导致非线性平面霍尔效应的出现[15,78].Yasuda等[82,83]在反铁磁/拓扑绝缘体异质结构中也观察到了非线性霍尔效应,不同的是,他们将其物理机制归结为磁振子的不对称散射.针对实验上出现的现象,我们研究组提出了两种不同的机制[41,79]:其一,在考虑非线性动量项的基础上,由外加磁场导致的狄拉克锥的倾斜;其二,在拓扑绝缘体薄膜中考虑上下表面的耦合,由外加磁场导致的狄拉克锥的位移效应.上述两种不同的机制均能诱导线性和非线性平面霍尔效应,且两种机制之间存在着竞争.综合目前已有的理论,我们可以将非线性平面霍尔效应的起源归结为外禀贡献和内禀贡献,下面分析几种代表性的机制.

3.1 外禀机制

3.1.1 非线性Drude项

在物理机制方面,这种非线性平面霍尔效应所产生的原因被总结为:在与自旋共线的面内磁场中,由于自旋动量锁定和时间反演破缺的共同作用,非线性横向自旋电流将转换为电荷电流[15,78].下面是该物理机制的详细解释.

值得注意的是,当色散是关于k的线性依赖关系时,面内磁场仅在k空间中平移狄拉克点,并不能使自旋电流和电荷电流之间发生转换.只有考虑动量的高阶项如拓扑绝缘体的六角翘曲效应时,非线性平面霍尔效应才会出现.

3.1.2 位移效应机制

我们研究组还发现,在拓扑绝缘体薄膜中考虑上下表面态的耦合作用,由面内磁场导致的狄拉克锥的位移效应也能产生平面霍尔效应[79].该效应不仅存在于线性平面霍尔中,还能贡献非线性平面霍尔效应.这里暂且忽略拓扑绝缘体薄膜中高阶项的影响.在面内磁场的作用下,拓扑绝缘体薄膜的表面态的低能有效哈密顿量模型可表示为

其中,Δ是上下表面的耦合强度[84],τ(τx,τy,τz) 表示作用于上下表面的泡利矩阵,τ0和σ0为单位矩阵.由于面内磁场的作用,两个狄拉克锥在垂直于磁场B的方向上向相反的方向移动,如图11(a)所示.当两个狄拉克锥的部分重叠时,会在平行于磁场的方向上出现非零的净自旋极化,如图11(b)所示.根据图11(c)所示的净自旋极化|S|可以发现,在弱磁场下(即B的取值相对较小),沿磁场的方向存在着明显的净自旋极化.由于自旋动量锁定,狄拉克电子的电流所诱导的自旋(红色细箭头)和净自旋(红色粗箭头)之间形成自旋阀的结构,如图11(b).该自旋极化引起各向异性的自旋输运,进而导致横向平面霍尔效应的产生.由位移效应贡献的平面霍尔电阻与角度的关系虽然不是余弦或正弦关系,但依然保持着 2π 的振荡周期.

图11 (a)平面磁场作用下的位移效应Dirac 锥的变化示意图;(b)位移效应的自旋阀结构示意图;(c)磁场B 相关的净自旋极化|S| [79]Fig.11.(a) Schematic illustration of Dirac cones of top and bottom surfaces in topological insulator thin films with shift effect induced by the in-plane magnetic field B;(b) schematic pictures of spin valve structure with shift effect;(c) the dependence of net spin polarization|S| on the field strength B.Image cited from Ref.[79].

3.1.3 贝里偶极子机制

3.1.4 磁振子散射机制

在前面提及的机制中,没有涉及温度的影响.当考虑有限温时,磁振子散射可以诱导拓扑绝缘体产生非线性平面霍尔效应[82,83].由于阻尼自旋轨道耦合贡献可以忽略,因此,在平面磁场的作用下,二阶非线性霍尔电压将主要来源于非线性传导其在CBST/BST/InP 样品上与平面内磁场和电场的相对角度依赖关系如图12(a)所示.

二阶非线性平面霍尔电阻的起源可用不对称的磁振子散射进行解释[82,83],如图12(b)所示.当J//M时,一方面,当B点附近的电子(群速度为正、角动量为 +1/2)散射至D点附近时,其动量将变为 -1/2.由于自旋动量锁定和角动量守恒的影响,该过程将必然伴随着角动量为 +1 的磁振子发射.相反地,当它从D点处散射到B点附近时,则必须吸收磁振子.这种不对称的磁振子散射将导致弛豫时间的不对称,进而引起D点和B点周围电子分布的不对称.这种不对称的磁振子散射模型可以用来评估二阶非线性平面霍尔电阻.

3.2 内禀机制

3.2.1 贝里联络极化机制上述提及的各种机制均属于外禀机制,因此与弛豫时间相关.最近,与散射无关的内禀非线性霍尔效应引起人们极大的兴趣[88-91],研究者们用贝里联络极化(Berry-connection polarizability,BCP)来表征这一效应.当施加平面磁场时,在塞曼效应的耦合下,内禀的非线性霍尔效应推广至非线性平面霍尔效应[18].在外加电场的作用下,贝里联络被附加上电场的修正项Gab(k)Eb,其中Gab(k)为贝里联络极化张量,具有如下形式:

Huang 等[18]通过对称性分析得到了内禀非线性平面霍尔电流与磁场和电场的相对角度依赖关系,相比于外禀诱导的非线性平面霍尔效应,他们给出了不同的角度依赖性.重要的是,内禀非线性平面霍尔电流被认为可以作为表征不支持非线性反常霍尔效应这一类材料的工具.

至此,我们介绍了拓扑材料中线性和非线性平面霍尔效应相关的主要物理机制,这些机制虽然分别从线性和非线性平面霍尔效应进行讨论,有些机制其实可以同时导致线性和非线性平面霍尔效应,比如,位移效应不仅可以导致非线性平面霍尔效应,也可以导致线性平面霍尔效应,手征反常不仅可以出现在线性平面霍尔效应中,也可以出现在非线性平面霍尔效应中.本文将其总结如表1 所列.总体来说,平面霍尔效应目前仍是一个非常活跃的研究领域,非线性平面霍尔效应更是一个相对较新的研究领域,各种新的物理机制正不断地涌现,它们彼此相互补充并被用于解释相关实验现象.

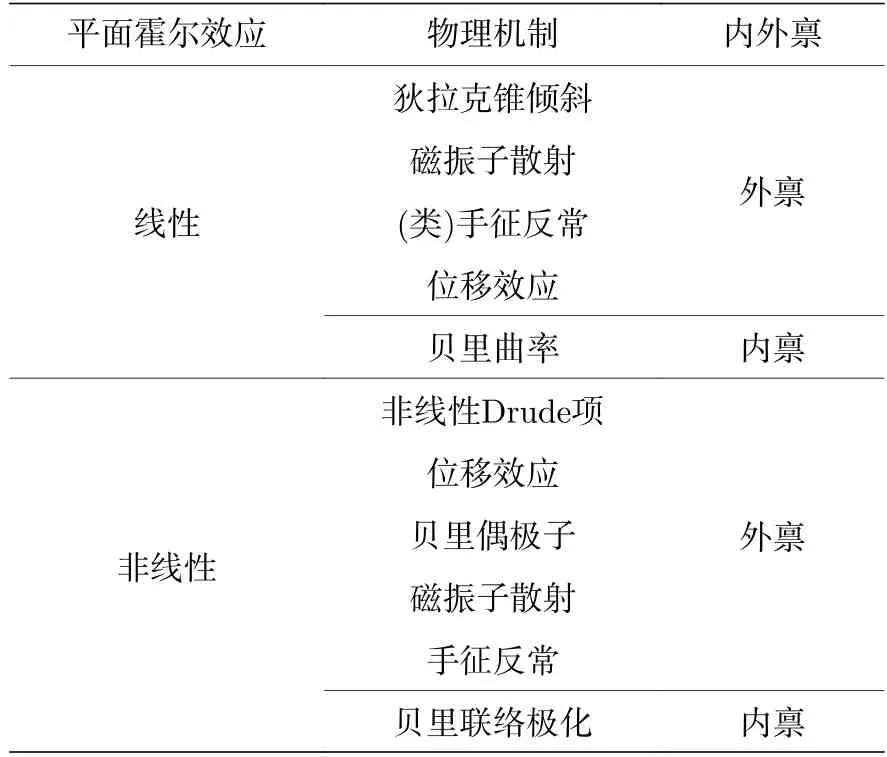
表1 拓扑材料中的线性和非线性平面霍尔效应的主要物理机制Table 1.Main physics mechanisms of linear and nonlinear planar Hall effect in topological materials.

4 实验进展

非磁拓扑材料中的线性平面霍尔效应最早是由Taskin 等[30]在三维拓扑绝缘体 Bi2-xSbxTe3中观测到的,他们发现拓扑绝缘体表面态的PHE 会随着磁场方向的变化呈现出六重对称性的振荡,这与材料的晶体对称性和狄拉克锥的形状一致.通过分析霍尔电阻率的温度依赖性和磁场依赖性,确定了电子态的有效质量和自旋轨道耦合强度,以及狄拉克锥的能隙大小与畸变程度.不久,Kumar 等[92]在Weyl 半金属GdPtBi 中观察到了比铁磁材料中大得多的线性平面霍尔效应,这可以归因于材料中的手征反常和贝里曲率.他们发现,在施加平行于[111]方向的电场和磁场后,出现了负磁阻率和量子振荡.另外还发现,PHE 的振幅不仅会受到手征反常的影响,还会受到轨道磁阻的影响.因此,要观察到明显的PHE,需要选择轨道磁阻较小的Weyl 半金属.2018年,Singha 团队[93]报道了一种Type-II 型拓扑狄拉克半金属 VAl3的磁输运性质.他们通过四探针技术测量了其单晶样品的线性平面霍尔电阻率,并发现VAl3可以出现很大的、不饱和的磁阻效应,以及高迁移率的电子和空穴型载流子.最重要的是观测到了一个很大的线性平面霍尔效应,作者认为平面霍尔效应是一种可以用来鉴别拓扑半金属中狄拉克/外尔费米子的有效方法.随后一年,Yin 等[27]报道了反铁磁半导体MnTe 的线性平面霍尔效应,并揭示了其自旋轨道耦合和能带各向异性.

2020年,Wadehra 等[28]在LaVO3-KTaO3的极性-极性界面上观测到了线性平面霍尔效应和各向异性磁阻,表明材料中存在强自旋轨道耦合.实验团队用X 射线衍射和透射电子显微镜等方法表征了其分子结构,并通过霍尔探针测量了不同温度和磁场下的电阻率和霍尔系数,观测到PHE 和AMR 特征信号.2021年,人们在Dirac 反钙钛矿Sr3SnO 中也观察到了类似拓扑绝缘体的六重振荡线性平面霍尔效应[94].实验组测量了不同厚度Sr3SnO 薄膜的电阻率张量,并发现在平面磁场下,纵向电阻率和横向电阻率都显示出多个谐波,其中包括二阶、四阶甚至六阶.这些谐波具有对不同磁场、温度以及薄膜厚度的依赖性,表现出了复杂的微观机制.初步的研究表明:自旋轨道耦合的J3/2费米子可能在其中起到了重要的作用,该实验进一步展现出了PHE 的丰富性,并推动了对拓扑材料中更高阶谐波的进一步研究.最近,人们在反铁磁拓扑绝缘体MnBi2Te4薄片中观察到了一种具有 π/2 周期的线性平面霍尔效应[95],并指出其来源于体态Dirac 电子的拓扑轨道磁矩.实验发现,在弱磁场下PHE 具有 π 周期和正的幅值,类似于非磁性拓扑绝缘体中表面态的PHE.但在强磁场下,PHE 的周期会变为 π/2 并且振幅会变成负.此外,随着温度的变化,由于体态和表面态之间的竞争,PHE 和各向异性磁阻的振幅和相位都发生了非平庸的演化.

非线性平面霍尔效应最早是由He 等[15]在拓扑绝缘体Bi2Se3中发现的,该效应源于非线性自旋流向电荷流的转换.非线性霍尔电阻与外加电场和磁场成线性比例,并与外加磁场和电场的相对角度呈余弦关系,因此可用来探测自旋纹理.这种非线性平面霍尔效应存在于非中心对称的材料中.最近,Kozuka 等[96]于室温下在中心对称的狄拉克半金属SrIrO3薄膜中也观察到非线性平面霍尔效应,与在Bi2Se3上观察到的结果一致[15,78].Kozuka等将这种现象归结为界面上的反对称自旋轨道相互作用引起的动量相关的自旋分裂,这会进一步导致两个狄拉克带中出现复杂的自旋纹理.因此,双线性的磁电效应可以用于捕获复杂的自旋纹理[96],并在不同的镜面对称性下表现出各向异性的非线性平面霍尔效应[96,97].这也表明:在界面上具有强自旋轨道相互作用的材料中,通过打破局部反转对称性便可引起非线性自旋电荷的转换.Li 等[98]在室温下于InSb/CdTe 异质结构中研究了由界面Rashba 自旋轨道耦合引起的非互易磁输运现象,同样测得与平面角度呈余弦关系的非线性平面霍尔电阻.

最近,人们在磁绝缘体/拓扑绝缘体异质结构中也观察到了非线性平面霍尔效应[99].初步的研究表明:该效应与拓扑绝缘体表面态中磁近邻效应诱导的交换能隙和平面外的自旋纹理有关,可用于探测磁绝缘体/拓扑绝缘体异质结构中磁近邻效应.在不同衬底上的薄膜中,实验上观测到的二次谐波霍尔电阻对磁场B呈现出显著不同的响应,具体表现为:1) 在Tm3Fe5O12和Y3Fe5O12/Bi2Se3样品中测得的非线性平面霍尔的幅值比在Gd3Ga5O12/Bi2Se3样品中测得的要大1 个数量级;2) Tm3Fe5O12/Bi2Se3的非线性霍尔电阻与面内磁场呈线性相关,而Y3Fe5O12/Bi2Se3的非线性霍尔电阻除了与磁场呈线性依赖之外,在零场附近有一个额外的磁滞回线.虽然上述实验现象可通过翘曲效应和电子-空穴不对称诱导的非线性平面霍尔效应机制进行解释[15,79],但是都无法解释在Tm3Fe5O12和Y3Fe5O12/Bi2Se3样品中非线性平面霍尔效应大小的增强.与磁相关的机制是磁振子的散射机制[82,83],该机制可以解释Y3Fe5O12/Bi2Se3在零场附近的磁滞回线,但在Tm3Fe5O12/Bi2Se3样品中磁振子沿z方向极化,无法参与自旋面内极化的表面态电子的散射过程.因此,磁振子散射机制也无法同时解释两种磁性衬底的结果.目前仍无可靠的理论机制对其进行统一解释,需进一步进行实验和理论研究来揭示其潜在机制.

目前,线性平面霍尔效应的实验研究已经取得重大进展,这也推动着人们更进一步地研究非线性平面霍尔效应.虽然非线性平面霍尔效应的相关实验较少,但我们可以从非线性磁电阻的角度入手.当非线性磁电阻存在各向异性时,理论研究表明也可能存在非线性平面霍尔效应,这在一定程度上也能推动相关实验的进展.

5 总结与展望

本文介绍了平面霍尔效应的若干物理机制,并总结了最新的实验进展.可以发现,对于线性平面霍尔效应而言,实验与理论的结合已经取得了重大的进展,在众多拓扑材料中观测到的PHE,大多数都能和理论结合在一起.但是对于线性PHE 更进一步的理论研究,如带间度规项或是类手征反常项的贡献,亦或是未知机制与现有机制的相互竞争作用,还有待进一步的探究.

对于非线性平面霍尔效应而言,在给定外加电流(或电场)的情况下,霍尔电压与平面内的磁场相对于电流的角度θB呈现出余弦关系.部分研究表明,在弱磁场时,霍尔电阻与磁场强度呈线性关系;也有研究表明,在反铁磁衬底上,霍尔电阻在零磁场附近出现了磁滞回线,并且在弱磁场时随着磁场的增大而增强,但这种增幅并不遵循线性规律.不同的是,所有实验在强磁场时均得到了非线性的关系,但其理论机制还有待进一步研究.

目前,现有的理论仍无法完美地解释实验上的各种现象,这意味着理论工作还需不断发展和完善.目前最大的问题是同一系统中存在多种物理机制,如何将多种机制统一成一套完善的理论是当下值得探讨的问题.此外,上述理论机制均在半经典理论的框架下进行,所得到的非线性平面霍尔效应主要为带内贡献(如非线性Drude 贡献、贝里偶极子、贝里联络极化),是否存在带间贡献(如注入电流、位移电流)? 这也是值得研究者们深入探讨的一个问题.最近,人们在三维拓扑半金属中发现了由类手征反常[70]、洛伦兹力[100]所导致的线性平面霍尔效应.那么,三维拓扑半金属中是否也存在相应机制的非线性平面霍尔效应? 这还有待进一步研究和探讨.

总而言之,平面霍尔效应理论推动了量子输运和拓扑物理的研究,也为电子器件的制备提供了很多有趣的应用前景.非线性平面霍尔效应的概念已经在大量的实验中得到了验证.在理论方面,我们急需应对的是对其物理机制的全面理解,这些研究不仅能够促进实验的进展,还能够加速非线性平面霍尔效应的应用进程.