基于多参数融合的风电机组齿轮箱油温预警方法

王 健，李富源，黄 鑫，娄 霄

(国能长源湖北新能源有限公司，随州 432700)

0 引言

风电机组的状态监测和故障诊断是保证机组能够长期稳定运行和安全发电的关键。随着风机运行年限的增加，受油品状态、冷却性能、运行环境等因素的影响，齿轮箱油温超限的故障隐患也不断增加[1]。通过监测齿轮箱油温变化，实现油温超温的提前预警，可有效的减少故障。

对于风电机组齿轮箱的温度预警的研究，国内外学者主要集中在基于主轴承温度的故障预警以及基于齿轮箱油温的故障预警。基于主轴承的温度预警常采用PSO-BP神经网络模型[2]、GA-BP神经网络模型[3]、ANN模型[4]、DBN模型[5]、CNN模型[6]、LSTM模型[7]建立温度预测模型，采用主成分分析法、特征提取法、皮尔逊法、最大互信息系数法确定模型的输入[2-5,8]，采用加权平均法、残差值、概率分布法[5-7]确定报警阈值。对于齿轮箱油温的故障预警，文献[9]通过建立基于概率统计分析的齿轮箱油温正常行为模型，并根据不同工况设定不同的异常阈值，采用时序滑动窗口实现对温度的预警。文献[10]通过建立齿轮箱油温回归预测模型，依据实际运行数据与预测数据的偏差，按照指定的策略进行故障预警。文献[11]提出了一种基于异常数据清洗与动态神经网络的建模方方法，采用统计过程控制法分析残差，根据残差的特征分布计算预警阈值。文献[12]提出了基于PCA和动态神经网络的齿轮箱油温趋势预测模型，采用SPC方法控制模型的在线学习行为，实现对齿轮箱油温的趋势预测。

本文选用某风场风机SCADA系统中的运行数据，利用相关性分析法确定模型的输入，采用imPSO-BP建立齿轮箱油温故障预警模型，结合加权移动平均法（Weighted Moving Average,WMA）、核密度估计法（Kernel Density Estimation,KDE）分析预测值与实际值的残差绝对值，从而确定预警阈值。最后，通过实际案例对比了imPSO-BP模型与PSO-BP模型的预警效果。

1 数据集的建立

受风速、天气等因素的影响，风机监测数据具有一定的随机性[13]。为建立齿轮箱油温故障预警模型，需要考虑所有对齿轮箱油温产生影响的变量。在统计学上，若需反应两个变量之间的相关性，可进行相关性分析[14]。本文运用最大互信息系数（Maximal Information Coefficient,MIC）对风机SCADA系统的历史数据进行相关性分析，其定义如下：

式中：α、β为在A、B方向上划分网格数量，p(A,B)表示变量A、B的联合概率，p(A)、p(B)分别表示变量A、B的边缘概率密度，λ为变量，MIC(A,B)表示相关性系数。若MIC(A,B)≥0.95，表示变量A、B显著相关；若0.95＞MIC(A,B)≥0.8，表示变量A、B强相关；若0.8＞MIC(A,B)≥0.5，表示变量A、B中度相关；若0.5＞MIC(A,B)≥0.3，表示变量A、B弱相关；MIC(A,B)＜0.3，表示变量A、B无相关。

风电机组SCADA系统每次记录23个参数10分钟平均值。这些数据可以分为3类：1）温度参数，包括：齿轮箱入口油温(P1)，齿轮箱输入轴轴温(P2)、齿轮箱油温(P3)、齿轮箱输出轴轴温(P4)、发电机轴承A/B温度(P5,P6)、发电机定子绕组U1/U2/V1/V2/W1/W2温度(P7,P8,P9,P10,P11,P12)、主轴齿箱侧温度(P13)、主轴叶轮侧温度(P14)、变桨轴温度1/2/3(P15,P16,P17)；2）工况参数，包括：发电机速(P18),叶轮转速1/2(P19,P20)，机舱振动值X/Y(P21,P22)；3）风力参数，包括：风速(P23)。通过某风场风机SCADA系统的历史数据计算出各参数与齿轮箱油温的相关性系数，选择相关性系数大于0.8的参数作为模型的输入。选择的模型输入参数如表1所示。

表1 相关性系数表

2 故障预警模型建立

对SCADA系统历史数据进行相关性分析得到模型输入之后，建立基于imPSO-BP神经网络的齿轮箱状态预测模型。采用健康时刻的历史数据对神经网络模型进行训练，得到输入参数与齿轮箱油温之间的映射关系。模型训练好之后，向训练好的网络中输入风机的实时数据，实际值和模型预测输出之间的残差被处理为监测指标。再通过WMA与KDE对残差序列进行处理得到预警阈值。在监测过程中，输入测试数据，将残差与之前定义的阈值进行比较。如果残差在阈值范围内，表明风机处于健康状态；如果残差在连续时间内超出预警阈值，则认为风机出现故障，并进行故障预警。在监测过程中具体流程如图1所示。

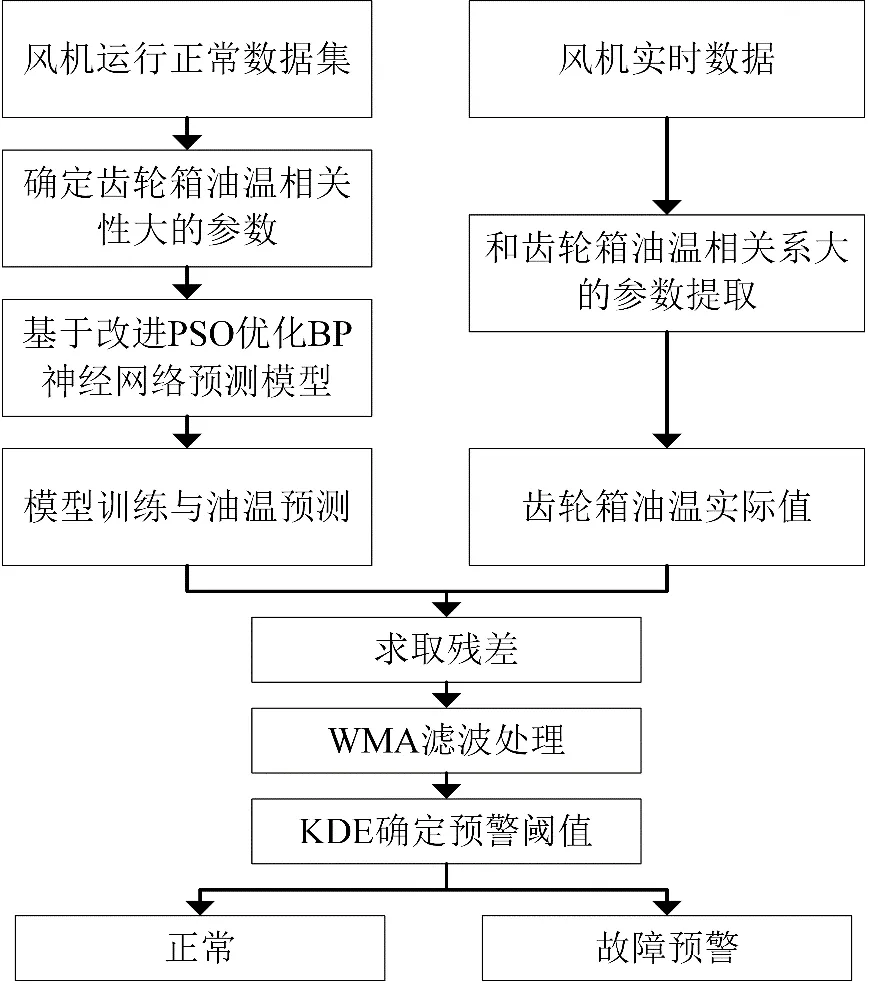
图1 齿轮箱油温故障预警模型

2.1 基于imPSO-BP神经网络的建立

1）BP神经网络模型的建立

以表1的参数作为模型的输入，齿轮箱油温作为输出建立BP神经网络模型。输入层为6个神经元，即对应表1中的6个参数；隐含层经过多次训练后选取了1层隐含层，神经元个数为8；输出层神经元个数为1，表示齿轮箱油温，如图2所示。网络的训练误差函数采用均方差函数，训练算法采用LM算法，隐含层的传递函数采用Sigmoid函数，输出层采用purelin函数。

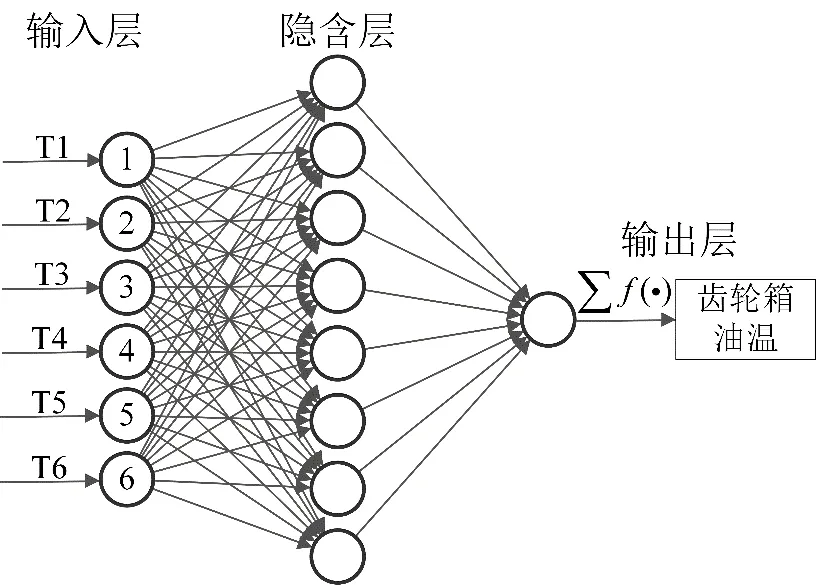
图2 BP神经网络结构

2）粒子群算法的改进

粒子群算法[15]是由Kennedy和Eberhart于1995年提出；学者在此基础上引入惯性权重因子w，称为基本粒子群算法，其惯性权重w和粒子速度更新公式为如下：

式中：wmax和wmin为惯性权重的最大值和最小值，MaxIt、iter为最大迭代次数和当前迭代次数，c1、c2为学习因子，r1和r2为服从[0,1]上均匀分布的随机数。

因线性惯性权重对全局搜索和局部搜索没有侧重性，考虑到算法初期需进行大范围的全局搜索，后期又需要较强的局部搜索能力，同时需加快算法的收敛速度。本文引入非线性sin曲线调整PSO的惯性权重w，sin曲线的斜率先增大后减小，这种变化趋势可使得粒子首先侧重全局搜索，随后侧重局部搜索，有利于粒子群快速搜索到全局最优。改进公式如式(3)所示：

3）imPSO优化BP神经网络

因BP神经网络受权值、阈值的影响较大，采用imPSO对其进行寻优，以提高齿轮箱油温的预测性能。算法的步骤如下：

（1）初始化BP神经网络。对式(1)中构建的网络进行权值和阈值的初始化。

（2）输入参数的归一化处理，即将输入参数转化为[-1,1]区间内。

（3）粒子群参数初始化。粒子群算法的初始化参数设置如下：种群规模设置为30，最大迭代次数MaxIt=100，粒子的初始速度为0，学习因子c1=c2=0.55，最大权重wmax=0.8，最小权重wmin=0.4，最大限制速度Vmax=1。

（4）构建BP神经网络权值和阈值优化的适应度函数。设置预测值与实际值之间残差绝对值的大小作为适应度函数。

（5）计算各粒子的适应度值，对个体最优和全局最优位置进行搜寻。

（6）按照式(3)进行权重和速度的更新。

（7）重复步骤（5）、（6），当满足设定的终止条件时，输出BP神经网络权值和阈值。其中，终止条件包括设置的最大迭代次数和连续5代适应度函数值小于设定值

（8）将步骤（7）得到权值和阈值输入到BP神经网络，并进行网络的训练。

2.2 网络的训练与结果分析

将第1节得到的输入参数，输入到2.1节建立的imPSOBP神经网络模型中进行训练。训练数据选取某风场8月1日至8月24日的数据用于模型的训练，8月25日至8月31日的数据用于模型的测试，数据每隔10min存储一次。训练集样本数据大小为3456，测试集数据大小为1008。采用平均绝对百分比误差(MAPE)、均方根误差(RMSE)、决定系数(R2)评价模型的训练结果[16]，其计算公式分别如式(4)～式(6)所示：

为验证改进的PSO-BP神经网络模型的有效性，对比了PSO-BP神经网络模型与imPSO-BP神经网络模型的训练效果，两种模型的预测结果与期望输出结果如图3所示。风电机组在健康状态下，两种方法的预测输出齿轮箱油温曲线与实际油温曲线基本吻合。

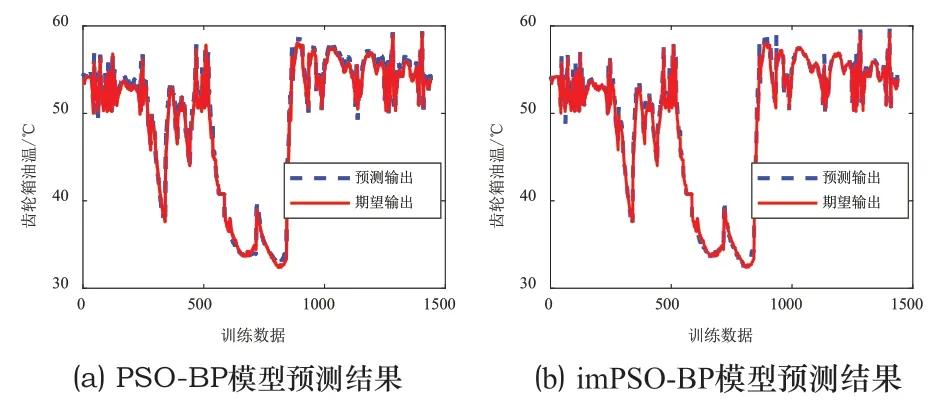
图3 模型预测结果

将两种模型的预测输出结果与期望输出结果分别求取残差序列，并分别计算两种模型的评价指标，得到残差序列如图4所示，评价指标值如表2所示。

图4 预测值与期望值残差

表2 评价指标对比

从三个评价指标和最大残差值来看，imPSO-BP 模型的预测精度优于PSO-BP模型。主要表现在：相较于PSO-BP，imPSO-BP的MAPE指标降低15.09%，RMSE指标降低12.5%，R2指标提高0.17%，最大残差指标降低35.93%。这是因为imPSO在优化过程中首先侧重全局搜索，随后侧重局部搜索，有利于快速找到BP神经网络的最优权值和阈值，这使得模型的预测输出与实际输出之间误差更小，相关性更高。

2.3 残差的滤波处理与阈值的确定

为消除随机因素对预警效果的影响，使用WMA对残差绝对值序列进行平滑处理，WMA表达式如式(7)所示：

式中：Δt表示滤波输出，τi表示数据对应的权重值，n表示窗口大小，Δt-n+i表示滤波样本值。

选用KDE确定预警阈值的大小，KDE估计算子如式(8)所示：

式中：xi表示给定样本，表示平滑因子或带宽，H表示核函数，n表示样本个数。

3 实验验证与结果分析

输入含故障的数据到训练好的PSO-BP[17]与imPSO-BP模型中，包含故障当天数据、故障前3天数据、故障后3天数据，共1008个数据点。两种模型的预测输出与期望输出结果如图5所示。

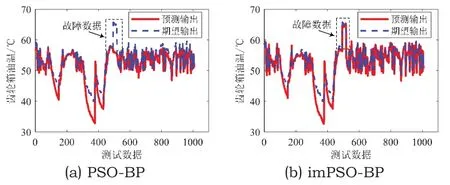
图5 含故障数据模型预测结果

分析图5(a)可知，在齿轮箱油温处于正常状态时，PSO-BP模型的预测值与期望值之间的误差较小，大约在故障前150个点及故障点处误差突然增大。分析图5(b)可知，对于imPSO-BP模型，仅在故障前150个点左右出现误差值的突然增大。误差的突然增大是因为故障即将出现时，输入的多参数时间序列与正常序列有较大的偏差，这种偏差会改变输入参数与输出参数之间的映射关系，从而导致误差变大。利用这个特点，可达到齿轮箱油温故障预警的目的。而对于PSO-BP模型出现两次误差大误差的情况，是因为PSO算法对于权重与阈值优化时无法实现快速寻优，导致在正常时刻模型出现大误差的输出。

将预测结果与期望输出结果求取残差绝对值，取WMA的窗口大小n=12，权重值=[0.026,0.045,0.071,0.1,0.12,0.138,0.138,0.12,0.1,0.071,0.045,0.026]，得到两种模型的WMA残差绝对值与残差绝对值如图6所示。

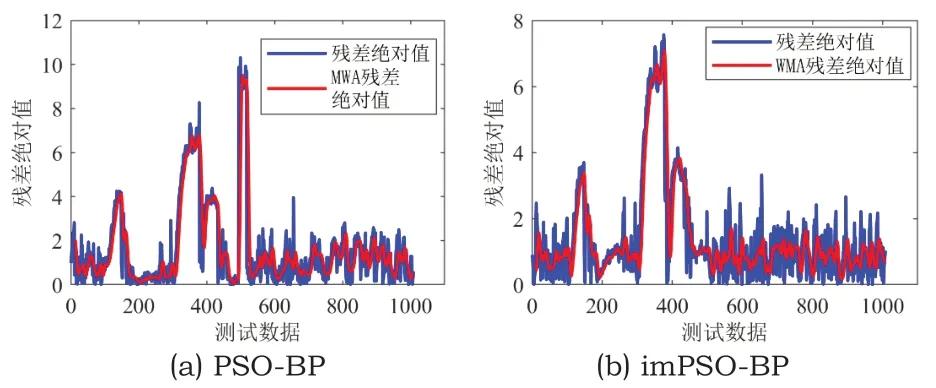
图6 WMA残差绝对值

选择KDE的核函数为逆累计分布函数，置信度为95%，两种模型的预警效果如图7所示。分析图7(a)可知，PSO-BP在采样点为351和501时出现超过阈值点，曲线超出阈值一段时间后很快落到阈值线以下；且第二次超出阈值的采样点出现在实际故障点后，属于误报警。分析图7(b)可知，基于imPSO-BP的故障预警模型可有效的实现对故障进行预警，且曲线超出阈值一段时间后没有落到阈值线下，说明预警结果较为可靠，不属于误报警。对于imPSO-BP模型，实际故障采样点为494，故障预警采样点为332，故障预警时间提前约27小时，故障预警效果优于PSO-BP模型。

图7 故障预警模型输出结果

4 结语

本文结合改进的粒子群算法和BP神经网络，提出了一种基于多参数融合的风电机组齿轮箱油温故障预警方法，可实现风电机组齿轮箱油温异常的提前预警。主要结论为：

1）根据风电机组SCADA系统的历史监测数据，采用相关性分析法确定了模型的输入参数。

2）建立了齿轮箱油温故障预警模型，并采用改进的粒子群算法对BP神经网络进行参数寻优。对比了PSO-BP模型与imPSO-BP模型的预测效果，实验结果表明：imPSO-BP模型提高了齿轮箱油温的预测精度。

3）通过实际的案例对该预警方法进行了验证，结果表明，imPSO-BP模型可实现齿轮箱油温故障的提前预警，预警时间提前约27小时。相较于PSO-BP模型，imPSO-BP模型预警结果更可靠，且不会出现误报警。