基于线结构光的飞机蒙皮铆接间隙自动检测

朱永国，卓 鑫，黄佳亮，胡元帆

（1.南昌航空大学 航空制造工程学院，南昌 330063；2.南昌航空大学 飞行器学院，南昌 330063）

0 引言

传统铆接质量检测方法是借助塞尺、千分表和卡规等设备进行手工检测。该方法依赖人工操作，效率低、检测精度较低，且易对工件造成损坏。与传统检测方法相比，数字化三维视觉测量技术具有精度高、效率快的优点[1-3]。DubinSki等采用视觉测量方法检测MC-21飞机蒙皮表面损伤质量，在飞机设计与维护阶段提供帮助[4]。Buckhorst采用数字化三维测量技术，通过无人机携带工业相机快速地检测飞机表面，并自动记录检测位置的索引图像和表面缺陷，提高了飞机装配效率[5]。Gramopadhye等采用主动和渐进式零件训练相结合的方案模拟机身视觉检测任务，以此改善视觉检查任务的决策性能[6]。崔焱等提出了基于机器视觉的手机盖板表面缺陷检测系统，通过机器臂携带工业相机采集手机盖板缺陷图像，利用图像差分算法快速识别出手机盖板表面缺陷，提高了检测效率[7]。杜雨馨等采用十字激光器实时解算掘进机机身位姿，得到机身相对于外部环境的倾角与偏离位移，实验表明该方法精度较高[8]。丁超等基于结构光原理对深孔类零件的内表面轮廓进行三维重建，深孔直径检测精度可达亚像素精度级别[9]。常树鹤等设计一套激光信息融合检测系统在线识别焊缝熔丝，在保证成形质量的同时，自动实时引导电弧焊路径，提高了生产效率[10]。徐尤南等提出了一种基于线结构光双目测量系统的管片位姿测量方法，通过双目测量系统获取管片边缘点的坐标，结合最小二乘法求解管片实际位姿，提高了管片位姿测量精度[11]。王坚等提出基于机器视觉的瞄准镜缺陷检测算法，实现了缺陷的快速识别与定位，缩短了检测时间[12]。

线结构光测量方式与其他测量方法相比，具有效率高、精度高、成本低的优点[13-15]，为此，本文在以上文献研究的基础上，以飞机蒙皮铆接装配质量控制为研究对象，提出一种基于线结构光的飞机蒙皮铆接间隙自动检测方法，以实现飞机蒙皮铆接间隙检测的自动化和数字化，克服传统飞机蒙皮铆接间隙检测方法效率低、精度差等不足。

1 飞机蒙皮铆接间隙自动检测系统搭建

图1所示为基于线结构光的铆接间隙自动检测系统，图2所示为飞机蒙皮铆接间隙自动检测流程。

图1 蒙皮铆接间隙自动检测系统

图2 飞机蒙皮铆接间隙自动检测流程

1）如图1所示，数字化测量设备主要包括一字线激光器、工业相机和工业机器人等。一字线激光器用于投射激光光条；工业相机用于获取铆钉光条图像；工业机器人控制线结构光传感器移动，实现飞机蒙皮铆接间隙连续自动检测。

2）计算机集成软件集图像采集、图像预处理、中心线提取、特征点检测、系统标定、坐标转换等功能于一体。

如图2所示，首先通过系统标定和图像处理技术获取相机内参、畸变系数、光平面系数和手眼关系矩阵，将坐标统一机器人基坐标系下表示；其次，根据铆钉分布特点和手眼关系矩阵规划自动检测路径，通过离线编程代码导入到机器人当中；然后，由机械臂带动线结构光传感器完成自动拍摄；最后，通过坐标转换和图像处理技术获取铆接间隙特征的三维坐标，以此求解出铆钉头与蒙皮表面之间的间隙。

2 测量模型构建

如图3所示，一字线激光器射点Q发出的激光在蒙皮表面上形成光条Lm，由于铆钉头检测范围小，且其为平面，可将光条Lm近似为直线。将Lm与Q点构成的平面记为光平面π，点P为光条直线Lm上一点，P点在成像平面上的投影点为P′。

图3 线结构光测量模型

图3中，各坐标系分别为像素坐标系Of-uv、图像坐标系O-XY、相机坐标系Oc-XcYcZc，OOc的长度即为相机的焦距f。

建立图像坐标(x,y)与像素坐标(u,v)的关系式：

式(1)中，(u0,v0)为图像坐标系原点O的坐标值；dx、dy为像元大小。

在成像过程中，由于相机自身制造的误差导致图像出现畸变。图像畸变按畸变方向可分为径向畸变和切向畸变。设(x,y)为畸变后的图像坐标，即图像真实坐标，(x′,y′)为畸变前的图像坐标，即图像理想坐标。当同时发生以上两种畸变现象时，真实坐标与理想坐标的关系可用下式表示：

式(2)中，k1，k2，k3为径向畸变系数；p1，p2为切向畸变系数；r为像点到中心点的距离，r2=x2+y2。

建立像素坐标(u,v)与相机坐标(xc,yc,zc)的关系式：

式(3)中，尺度因子cx=f/dx，cy=f/dy，s为倾斜因子，当像素坐标系u，v两轴垂直时s=0，M为相机内参矩阵。

光平面π方程用式(4)所示：

式(4)中，AL、BL、CL、DL为光平面方程参数。

联立式(1)～式(4)，即可求得点P在相机坐标系下的三维坐标值。

3 检测系统标定

要实现坐标统一在机器人基坐标系下在表示，需对铆接间隙自动检测系统进行标定，标定内容包括相机标定、光平面标定和手眼标定。

3.1 相机标定

相机标定用于获取相机内参和畸变系数，光平面标定用于获取光平面方程，结合相机标定和光平面标定即可求解相机坐标系中任意一点的三维坐标[16]。图4所示为相机标定流程。

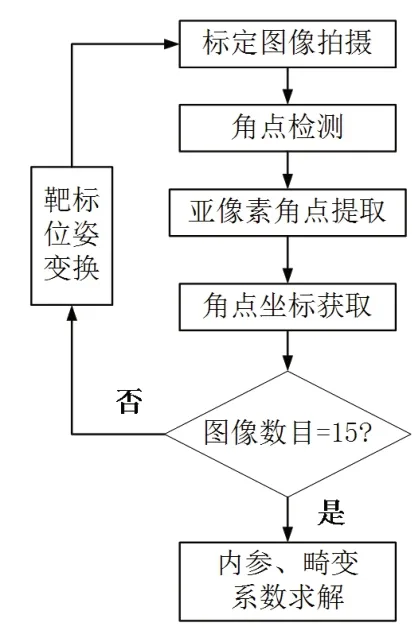
图4 相机标定流程

采用单应性矩阵H表示像素坐标系与相机坐标系之间的坐标转换关系：

式(5)中，H由旋转矩阵R和平移矩阵t组成：

定义hi为H的第i列，hji为矩阵第j行第i列的元素，ri为R的第i列，M为相机内参。

联立式(3)和式(5)，可得：

式(7)中，λ为放缩因子，r1、r2为正交向量。

利用式(7)，可得：

令Aa=M-TM-1，Aa为对称矩阵，可化简为：

式(9)中，aij为Aa矩阵中对应位置中的元素。

采用cholesky算法分解矩阵a，可得相机内参和畸变系数：

外参用式(11)表示：

畸变系数使用极大似然估计求解，最优化目标函数如式(12)所示：

式(12)中，m为角点个数，n为标定图片的数目，mij为第i幅图像第j个角点的坐标值，Pj为相机坐标系中第j个角点的坐标。

3.2 光平面标定

图5所示为光平面标定流程。

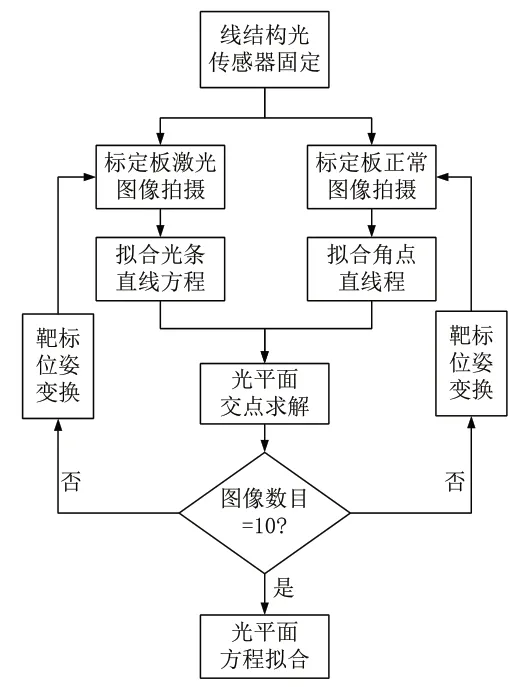
图5 光平面标定方程

光平面方程已由式(4)给出，采用奇异值分解拟合光平面方程。设交点的相机坐标为(xi,yi,zi)，若交点的个数为n，拟合步骤如下：

1）求所有交点的平均坐标

2）求交点坐标与平均坐标的差值矩阵Mv

3）设定目标函数d=min||MvX||，其中d为所有交点到光平面距离之和，其中X=[ALBLCL]T，约束条件为：||X||=1。

4）对差值矩阵进行奇异值分解。

式(15)中，Mv=UΣVT，U为n阶正交矩阵，Σ为n×3对角矩阵，V为3阶正交矩阵。且满足条件||VTX||=||X||=1。

5）当且仅当VTX=[000...1]T时，d取最小值，得：

6）将求解出的X与交点坐标代入光平面方程即可计算DL。

3.3 手眼标定

采用平面靶标对手眼关系标定，标定前需建立标定板坐标系Om-XmYmZm，该坐标系Xm轴、Ym轴与相机成像平面重合，Zm轴垂直于成像平面，标定板坐标系到相机坐标系的转换矩阵为Mb。

设q0、q1为末端执行器移动前后对标定板同一位置获取的一组点，其标定板坐标分别为(xm0,ym0,zm0)、(xm1,ym1,zm1)，基坐标分别为(xb0,yb0,zb0)、(xb1,yb1,zb1)。标定板坐标和基坐标的转换关系式为：

式(17)中，Ma0、Ma1和Mb0、Mb1分别为q0、q1两点所处空间位置相机坐标系到基坐标系、标定板坐标系到工具坐标系的转换矩阵。

由于机器人本体与标定板均未移动，两点的转换矩阵不变，可得：

对式(18)进行移项，可得：

综上式(17)～式(19)，可得：

式(20)中，Ma通过机器人示教盒获取，Mb为相机外参，可通过相机标定求解的内参和畸变系数计算得到。

联立式(8)与式(20)，可得：

根据李群理论[17]，对式(21)两边移项并取对数，可得：

令logMa=[Lα]、logMb=[Lb]。式(22)可化为[Lα]=Mc[Lb]McT=[McLv]，即：

当存在多组点时，利用最小二乘法进行求解，可得：

利用式(24)，可得：

将Rc代入式(21)，即可求解出tc。

4 自动检测系统坐标系统一

在铆接间隙自动检测系统中，须建立统一的坐标基准，由于机器人本体位置保持改变，因此可把坐标系统一在机器人基坐标系下。图6为机器人坐标系模型。

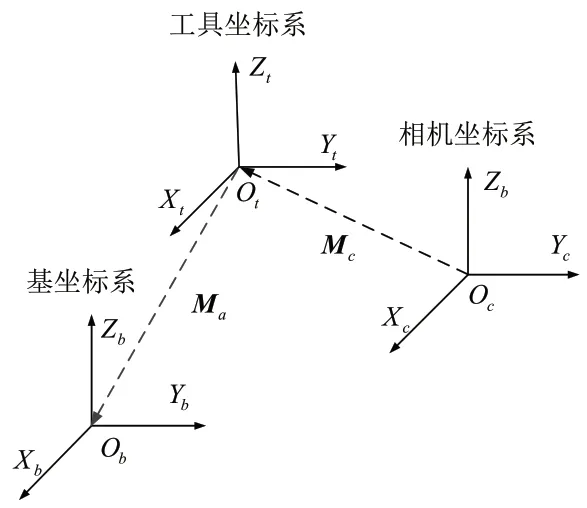
图6 机器人坐标系模型

图6中，Ob-XbYbZb为机器人本体上的基坐标系，Ot-XtYtZt为末端执行器上的工具坐标系。Ma为工具坐标系到基坐标系的转换矩阵；Mc为相机坐标系到工具坐标系的转换矩阵，Mc的表达式为：

式(26)中，Rc为旋转矩阵，tc为平移矩阵。

利用式(26)，得点P在基坐标系下的坐标(xb,yb,zb)为：

式(27)中，Ma为工具坐标系到基坐标系的转换矩阵。

5 铆接间隙检测

5.1 铆接间隙特征提取

1）中心线提取

铆钉光条图像经过二值化处理后所，光条宽度并未达到亚像素精度级别，为了便于铆接间隙特征点的检测，需提取光条中心。由于图像中光条区域占比不大，且呈直线特征。Zhang-suen骨架抽取法具有计算量小，精度高的优点，故采用Zhang-suen骨架抽取法[18]提取中心线边缘特征，再采用几何中心法确定光条中心。Zhang-suen算法根据图像的8邻域连通特性删除边界点，设图像中某一点的像素点为p，则p的8邻域示意图如图7所示。

图7 p的8邻域图

图像像素点的灰度值只有0和255两种取值，定义N(p)表示p点的8邻域中灰度值不为0的点的个数，S(p)表示将p点的8邻域以p1，p2，p3Kp8的顺序排列，相邻两个像素灰度值出现0到255的次数。中心线提取步骤如下：

（1）对图像进行遍历，当像素点p灰度值不为0时，计算N(p)、S(p)，并将这些像素点记录标记点群。

（2）删除符合下列条件的像素点。

（3）对删除部分像素点后的标记点群重新计算N(p)、S(p)。

（4）重复步骤（1）至（3），直到不再出现符合删除条件的像素点。

（5）按列遍历标记点群，将每列的几何中心作为中心点。

2）特征点检测

铆接间隙特征点是角点的一种，Harris角点方法能提取特征点[19]，为此引入Harris角点方法提取铆接间隙特征点，具体步骤如下：

（1）分别计算图像f(x,y)在x，y两个方向的梯度fx，fy。

（2）计算x，y方向上的梯度乘积。

（3）采用大小为n×n的滤波模板对图像进行遍历，并将梯度乘积与图像函数之积进行高斯加权求和，得到Mg，g为高斯滤波函数。

（4）计算每个像素点的Harris响应值R，R值为大数值时该像素点是角点。其中λ1,λ2为矩阵Mg的特征值，且λ1＞λ2，k为响应系数，k值越大，角点数量越少。

过滤出大于某临界值Rt的R值，这些像素点即为角点。

5.2 铆接间隙求解

铆接间隙求解如图8所示，Pl(xl,yl,zl)，Pr(xr,yr,zr)分别为铆钉头左右两侧的特征点，Lm为光条拟合直线，Pfl(xfl,yfl,zfl)，Pfr(xfr,yfr,zfr)分别为Pl，Pr到光条直线Lm的垂足点。由图可知左侧间隙值ΔGL为Pl，Pfl两点间的距离，右侧间隙值ΔGL为Pr，Pfr两点间的距离。

图8 铆接间隙求解模型

铆接间隙求解步骤如下：

1）使用图像处理技术获取铆接间隙特征点，包括铆钉头特征点Pl，Pr与蒙皮表面特征点群Ps，并结合求解的标定参数还原特征点在机器人基坐标系下的三维坐标。

2）设置一个距离度量Δd区分出Pl，Pr与Ps，其中点群Ps坐标为(xsi,ysi,zsi)。

3）对点群Ps进行空间直线拟合，拟合后的直线为Lm，设Lm直线方程为：

将式(33)转换为矩阵形式：

设点群Ps共有n组点，采用最小二乘法空间直线拟合求解Lm直线参数：

计算铆钉头特征点Pl，Pr到直线Lm的垂足Pfl，Pfr的坐标。PlPfl，PrPfr与直线Lm的方向向量之积为0，结合式(33)即可求得Pfl，Pfr的坐标：

左右两侧间隙值求解：

5.3 自动检测软件开发

以VS2010为开发平台，基于C++语言，结合Opencv与Basler API函数，开发图9所示的铆接间隙自动检测软件。

图9 铆接间隙自动检测软件模块设计

软件的部分界面如图10～图13所示。

图10 数据管理界面

图11 系统标定界面

图12 铆接间隙求解界面

图13 图像处理界面

6 实验

6.1 蒙皮铆接间隙自动检测系统搭建

基于以上的理论研究，构建图14所示的蒙皮铆接间隙自动检测系统。

图14 蒙皮铆接间隙自动检测平台

6.2 铆接间隙自动检测实验

铆接间隙自动检测系统选用图15的铝合金板铆接件进行实验，该铝合金板长53cm，宽30cm，铆钉排列数目为8×5。

图15 铝合金样板图

实验中选取左侧3列的15个铆接间隙值与参考理论值进行作差比较，其中参考理论值通过莱卡T-scan扫描获得。左侧间隙测量数据如表1所示，右侧间隙测量数据如表2所示。

表1 左侧间隙测量数据（mm）

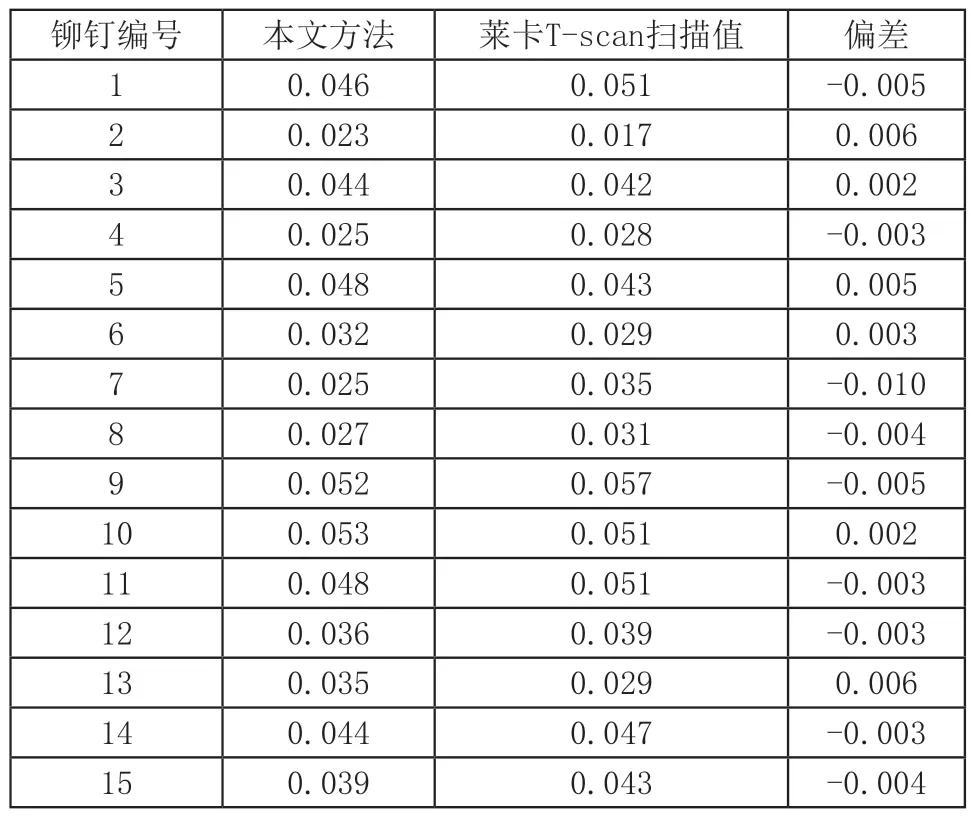
表2 右侧间隙测量数据（mm）

由表1和表2可看出，左、右侧铆接间隙检测误差的最大为0.006mm。经过计算可得，左侧铆接间隙的均方差为2.24×10-3mm；右侧铆接间隙的均方差为4.74×10-3mm。因此，构建的铆接间隙自动检测系统具有较高的准确度和工程应用可行性，能满足实际工程需要。且和T-scan方法相比，更经济，能自动检测。

7 结语

1）建立了基于线结构光的铆接间隙测量模型，引入Harris角点检测方法实现了铆接间隙求解，提出了线结构光铆接间隙自动检测方法。该方法可提高铆接间隙的检测效率，实现了飞机蒙皮铆接间隙的数字化和自动化检测，也能保证检测数据的可靠性和稳定性。

2）构建了铆接间隙自动检测实验平台，实验结果表明该方法具有较高的准确度和工程应用可行性，能满足实际工程需要。