负压爆炸载荷作用下固支钢板变形研究

2023-11-15谢守冬涂唱畅徐小猛李孝臣

高压物理学报 2023年5期

杨锐，汪泉，谢守冬，李瑞,4，涂唱畅，徐小猛，李孝臣

（1.安徽理工大学化学工程学院, 安徽淮南 232001；2.安徽理工大学土木建筑学院, 安徽淮南 232001；3.宏大爆破工程集团有限责任公司, 广东广州 510000；4.安徽理工大学煤炭安全精准开采国家地方联合工程研究中心, 安徽淮南 232001）

近年来，高原环境的军事演习增多，高原环境下的爆炸冲击毁伤问题得到国内外的高度重视。在处理飞机、船舶、车辆等复杂结构在爆炸作用下的毁伤问题时，可将这些复杂结构视为装甲类目标，以其表面的板结构作为研究对象，通过实验、数值模拟和理论分析开展研究[1–2]。Jacob 等[3]研究了爆距和药量对爆炸载荷作用下固支圆板响应的影响。陈长海等[4]通过实验分析了方板在近爆载荷作用下的破坏模式，提出了破裂判别条件，从而预测了爆炸载荷作用下钢板是否失效。韩璐等[5]通过方板毁伤实验建立了不同毁伤模式下的数值模型。Wang 等[6]对聚异氰氨酸酯噁唑烷酮（polyisocyanateoxazodone，POZD）涂层钢板-钢筋混凝土板和普通钢板-钢筋混凝土板进行爆炸实验，分析了药量、POZD 厚度、钢板厚度和钢筋混凝土板厚度对POZD 涂层钢板-钢筋混凝土板抗爆性能的影响。Remennikov 等[7]采用液体球状炸药对钢板进行近爆实验，探讨了几种防护方案对实验结果的影响，并建立了工程模型。秦业志等[8]采用RKDG（Runge-Kutta discontinuous Galerkin）方法研究了柱状装药水下近场爆炸作用下单层钢板的响应特性。以往的模拟实验大多针对水下爆炸或常压下爆炸对板结构的毁伤[9–10]，对于高原、高空等负压环境下爆炸载荷与目标结构变形之间的关系研究较少。当炸药药卷从常压环境转移到负压环境时，为了平衡内外气压，药卷体积膨胀，密度降低，根据爆轰产物的JWL 状态方程[11]，装药密度降低会直接影响爆轰产物膨胀规律，同时，负压环境对冲击波的传播过程亦有影响，致使负压与常压下的毁伤实验结果有所不同。

本研究将对负压爆炸载荷作用下固支钢板的动态响应过程进行实验和数值模拟，以期为负压环境下爆炸冲击波威力等效评估、高原环境下目标毁伤评估等提供参考。

1 负压爆炸实验

1.1 实验设计

负压爆炸实验在可调真空度的爆炸容器内进行。固支方板作为模拟复杂防护结构的简化单元，采用Q235 钢制成，尺寸为1 mm×460 mm×460 mm，四周均匀分布20 个直径为16 mm 的螺栓孔。为实现方形钢板的边界固定条件，在爆炸容器中心平台上搭建钢制方形支座[4]，如图1(a)所示。由于存在夹板，因此实验中钢板的有效迎爆面尺寸为300 mm×300 mm。炸药采用乳化炸药，爆热为3 610.20 J/g，TNT 当量约为乳化炸药质量的0.862 9 倍[12]。用绳索将乳化炸药吊置在钢板上方，将容器抽至预期负压后静置2 h，将导爆管雷管插入炸药中心起爆。实验系统如图1(b)所示，实验工况如表1 所示，其中pe为初始环境压力，W为乳化炸药质量。

表1 实验工况Table 1 Experimental conditions

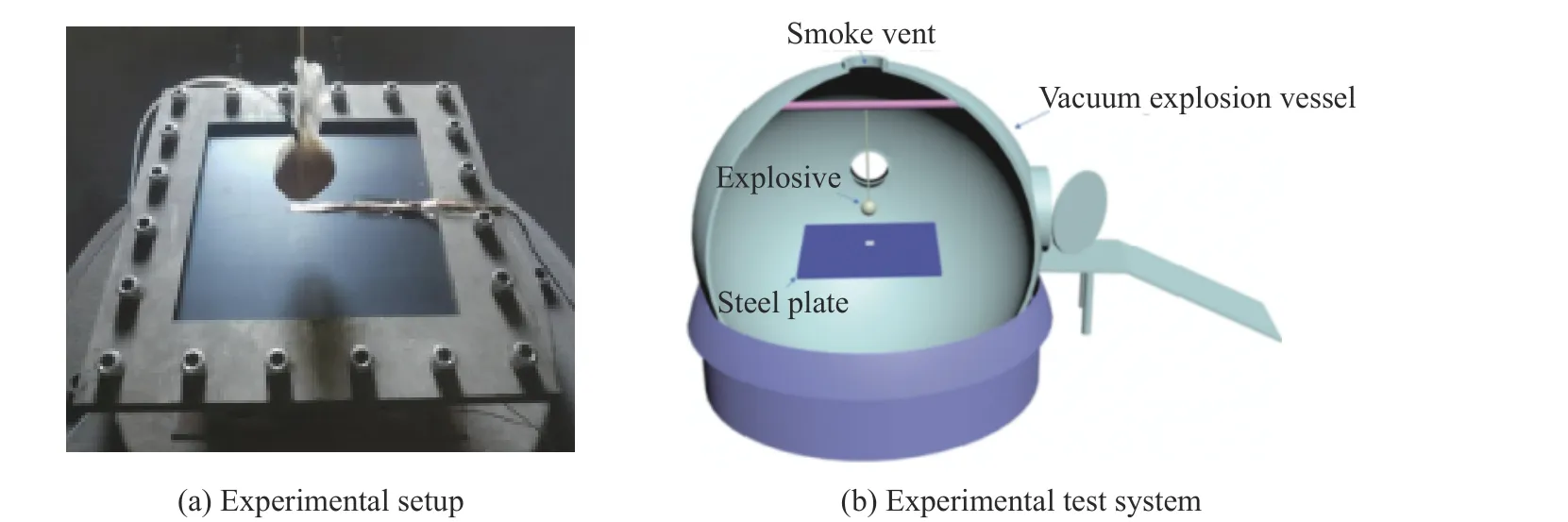
图1 实验示意图Fig.1 Schematic diagram of the experiment

1.2 固支钢板在不同负压环境下的变形破坏分析

图2 给出了工况1～工况3 下固支钢板的变形情况。可以看出，不同负压爆炸载荷作用下固支钢板均未穿孔，整体出现塑性大变形，迎爆面形成凹坑，即毁伤模式为塑性大变形毁伤[5]。当初始环境压力从101 kPa 降到60 kPa 时，钢板中心处凹陷程度下降。钢板四周固支端螺栓孔在垂直于固支边界并指向钢板中心的方向上出现明显的拉伸变形，且随着环境压力的下降，钢板四周的拉伸变形逐渐减小。钢板迎爆面对角线处出现明显的塑性铰线，塑性铰线延伸至中心，中心点为凹坑最深处，钢板表面无明显的爆炸产物灼烧现象。

在钢板中线上每隔1 cm 布置一个测点，测量钢板中线变形挠度γ。设钢板有效迎爆面的半宽为L，以钢板中心为原点、钢板中线为x轴，得到工况1～工况3 中钢板中线的变形轮廓，如图3 所示。在10～15 cm 区间（边缘区），3 种工况下钢板的变形程度相近；在0～10 cm 区间（中心区），3 种工况下钢板的变形程度不同，最大挠度位于钢板距离炸药中心的最近点（即钢板中心），初始环境压力为101、80、60 kPa 时，最大挠度分别为37、33、31 mm，最大挠度随初始环境压力的下降而减小。

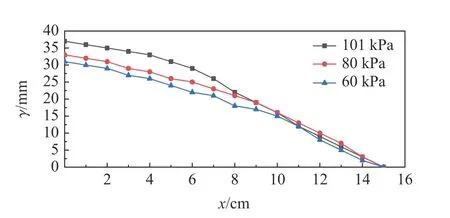
图3 钢板变形轮廓Fig.3 Deformation contours of steel plates

目前，通常用超压-冲量准则[13]衡量空气爆炸载荷对目标的破坏效应，即认为空气冲击波阵面的最大超压Δpm与比冲量i的共同作用满足某临界条件时目标破坏。炸药爆炸瞬间，爆炸产物剧烈膨胀并压缩周围空气，形成压力、密度、温度突跃的空气冲击波，其初始强度取决于爆轰波参数、介质的密度及可压缩性等特性。负压环境的典型特征是环境压力和空气密度低于常压。随着爆炸容器内压力的降低，冲击波阵面前未扰动的空气变得稀薄，冲击波峰值超压和比冲量减小[14]。因此，负压环境通过影响冲击波的传播过程对爆炸载荷起衰减作用。由于爆炸冲击波的比冲量决定实验后钢板的最大挠度[15]，所以钢板的变形程度随着环境压力的下降而减小。同时，环境压力下降时，爆炸产物膨胀速率下降变慢，空气冲击波速度变快。

工况4 增大了乳化炸药的药量并减小了爆距，可视为接触爆炸载荷作用。图4 给出了实验后钢板的破坏形貌。钢板中心部位呈花瓣状开裂，3 条长度分别为19.20、12.50、15.70 cm 的裂纹贯穿整个钢板，将钢板分成3 个破片，裂纹延伸至四周固支边界使钢板剪切断裂，有效抗爆面整体剪切失效，从支座上脱落并扭曲成团，毁伤模式为三花瓣状破口毁伤[5]。固支边界处的剪切断面光滑整齐，垂直于剪切断面方向出现明显的拉伸变形，沿着剪切断面方向出现细微的拉伸变形。相对于初始板厚，中心部位的裂纹边缘呈现明显的减薄现象。

图4 工况4 中钢板的破坏模式Fig.4 Damage mode of steel plates in case 4

1.3 动态极限应变

工况4 中，钢板中心部位的裂纹由拉伸断裂所致，边缘出现明显的减薄现象。根据双向应变假设，钢板的动态极限应变可由钢板开裂处的减薄率计算[16]。在开裂处取极小微元，其厚度为h，体积为hdxdy，设微元在x、y方向的应变分别为εx、εy，厚度方向由h变成h1，根据体积不变原理，有

假设微元在x、y方向上的应变是对称的，即εx=εy，可得

式中：εf为结构的动态极限应变。

测量3 个破片在开裂处的钢板厚度，如图4(b)所示，共取8 个测点，实验和计算得到的减薄率以及双向极限应变列于表2。考虑到钢板结构的受力和变形比较复杂，测点3 和测点8 的数据与其他测点的数据相差较大，因此将其舍弃，取其余6 个测点的双向极限应变的平均值作为钢板的动态极限应变，得到Q235 钢板的动态极限应变为0.269。由于结构的动态极限应变与材料属性、结构形式、加载方式等诸多因素有关，本研究所用薄钢板的尺寸较小，因此得到的双向极限应变0.269 是合理的。该结果仅适用于负压爆炸载荷作用下尺寸较小的固支薄钢板中心拉伸断裂情况，对Q235 钢结构在类似的爆炸载荷作用下的失效情况具有一定的参考价值。

表2 开裂处钢板厚度的测量结果Table 2 Measurement results of steel thickness at crack

1.4 失效条件

近场爆炸时，一般按有效冲量计算爆炸对目标的破坏作用。与单质炸药相比，乳化炸药在负压环境下的做功能力和破坏能力较弱，传统的基于TNT 等单质炸药提出的正压冲量公式无法准确预测乳化炸药爆炸冲击波的比冲量。文献[12]给出了乳化炸药在不同负压环境下的入射波正压比冲量公式

式中：装药质量W的单位为kg；R为比例距离，m；ph和p0分别为低压环境和标准大气压环境下的环境压力，kPa；is为入射波正压比冲量，Pa·s。计算刚性表面的爆炸冲击波时，其药量应按照空中爆炸时药量的2 倍[17]计算，若周围介质可吸收能量，则式(3)中的装药质量应当用2θW表示，其中：θ 是考虑爆炸能量耗散在空气中的份额所得出的材料系数，对于本研究中的钢板，θ 取1。入射波正压比冲量公式转化为

文献[18]给出了冲击波正规反射比冲量ir与入射波正压比冲量is的关系式，即ir=is(1+cos φ0)，其中：φ0为爆炸冲击波到钢板的入射角。本实验中，爆心距r=150 mm，钢板半宽L=150 mm，则0° ≤ φ0<45°。因此，不同环境压力下炸药爆炸冲击波的正规反射比冲量为

假设结构为理想的刚塑性体，当受到爆炸冲击波作用后，结构产生位移，直至速度为零时，全部动能转化为应变能。根据动量定理，单位体积最大速度v0=ir/ρh，其中ρ 为质量密度。

由工况4 可知，钢板中心发生拉伸断裂，中心处的应变率[19]为

本研究中，L=0.15 m。

设动屈服强度σd=ασ0，其中：σ0为准静态屈服强度，α 为应变率系数。α 由Cowper-Symonds 关系得到

式中：D为应变率常数，q为应变率指数。对于Q235 钢，q=5，D=40.4 s-1，σ0=235 MPa。

若结构的最大应变εm接近甚至超过极限应变εf，则认为结构破裂失效。根据刚塑性假设和能量准则，钢板中心点的单位体积应变能为σdεm。由于近爆时间极短，因此可以认为钢板获得的初始动能全部转化为应变内能

文献[4]中定义变量η 作为结构的破裂判别参数，η 的表达式为

失效应变采用1.3 节中的双向极限应变，即εf=0.269。当η<1 时，钢板仅发生塑性变形，未发生断裂失效；当η≥1 时，钢板发生断裂失效。

表3 给出了工况1～工况4 的失效判别条件参数。从表3 可以看出：工况1～工况3 中，η<1，说明3 种负压环境下固支钢板均未穿孔，整体未断裂失效，与实验结果一致；工况4 中，η>1，说明钢板断裂失效，与实验结果一致。通过测量负压爆炸载荷作用下金属板开裂处的厚度，可以计算出金属板的动态极限应变。根据刚塑性假设，由正规反射比冲量公式得出金属板获得的动能，进而根据能量密度准则计算出金属板在爆炸作用下瞬间形变的最大应变。当最大应变超过动态极限应变，即η >1 时，金属板断裂失效。当金属板处于近距离爆炸场时，已知金属板的性能参数，可以推算出负压环境下爆炸载荷作用下金属板断裂失效的最小起爆药量。值得注意的是，当选取的金属板厚度较薄，最大应变小于或接近动态极限应变时，金属板也可能断裂失效；当爆距过大时，爆炸载荷可视为均布爆炸载荷，金属板的断裂失效情况可能与局部爆炸载荷作用下的情况有所不同。

表3 失效判别式的相关参数Table 3 Relevant parameters for failure discriminant

2 数值模拟

2.1 一维空中爆炸及结果映射

采用结果映射Ramap 技术，建立一维楔形空气域模型，模拟不同环境压力下TNT 爆炸冲击波传播的初始过程，然后将一维结果映射到相同工况的三维模型中继续求解。通过映射可以提高计算效率，得到更精确的结果。一维楔形空气域模型及炸药网格如图5(a)所示。在欧拉空气域中设置半径为26.7 mm 的TNT，比例距离为3.0 m/kg1/3。如图5(b)所示，建立1/4 三维模型，包含空气和钢两种物质。空气域的长和宽均为150 mm，高为240 mm，综合考虑网格敏感性和模拟时间成本，将网格尺寸设置为2 mm×2 mm[20]，边界设为Flowout 透射边界。钢板迎爆面的长和宽均为150 mm，厚度为1 mm，钢板网格尺寸为1 mm×1 mm，在板边缘添加速度为零的约束条件。钢板采用Lagrange算法，板结构和空气域采用流固耦合算法。

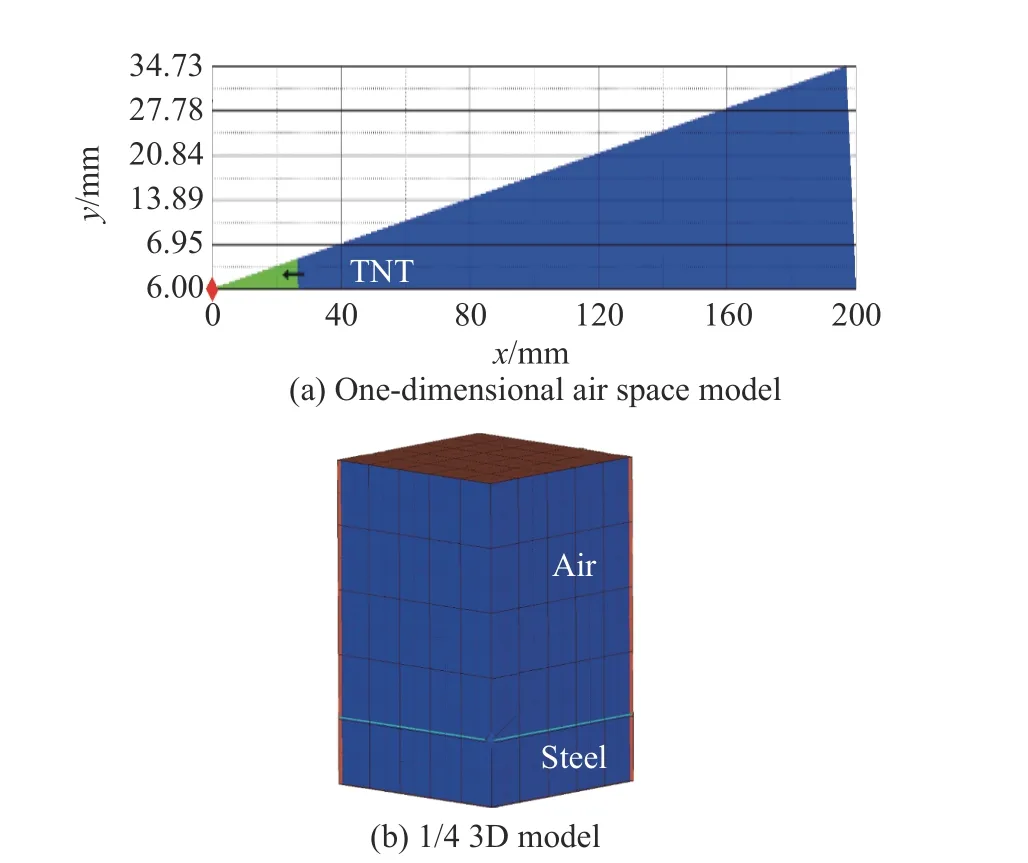
图5 几何模型Fig.5 Geometrical model

2.2 模型材料

TNT 采用JWL 状态方程描述，相关材料参数取自AUTODYN 标准材料模型库。钢板选用Q235 钢，采用Shock 状态方程描述，其参数取自AUTODYN 材料库，Johnson-Cook 强度模型参数列于表4，其中：ρs为Q235 钢的密度，A为初始屈服应力，B为硬化常数，n为硬化指数，C为应变率常数，m为热软化指数，Tm为熔化温度。

表4 材料参数[21]Table 4 Material parameters[21]

空气采用理想气体状态方程描述，即

式中：p为气压，K为绝热指数，ρa为空气密度，e为空气的初始比内能。不同压力环境下，空气的密度与压力之比相同，即

式中：下标i和j代表不同状态。

根据式(11)，通过改变空气的初始密度，可以实现不同的负压环境。表5 列出了不同初始环境压力对应的空气密度。

表5 不同环境压力对应的空气密度Table 5 Air densities at different environment pressures

2.3 数值模拟结果分析

图6 给出了在不同负压环境下钢板的变形情况。不同负压环境下，钢板均出现明显的塑性大变形，未产生穿孔破损，钢板中心点的挠度最大。当初始环境压力为101、80、60、40、20 kPa 时，钢板的最大挠度分别为34.7、32.9、30.6、28.3、27.9 mm；初始环境压力从101 kPa 降到80、60、40、20 kPa 时，钢板最大挠度分别减小5.3%、11.8%、18.4%和19.6%。随着初始环境压力的下降，冲击波传播过程中空气密度减小，爆炸冲击波的峰值超压和比冲量也减小，致使钢板整体形变程度呈下降趋势。

图6 不同负压环境下钢板的变形情况Fig.6 Deformation of steel plate under different negative pressure environments

图7 为钢板中心点速度曲线。当初始环境压力为101、80、60、40、20 kPa 时，钢板中心点最大速度分别为113.7、106.6、83.5、80.3、70.5 m/s，随着初始环境压力下降，钢板中心点最大速度减小。钢板中心点速度在0.66 ms 左右降至零以下，即开始反向运动，随后发生振荡，并逐渐衰减，最终停止运动。

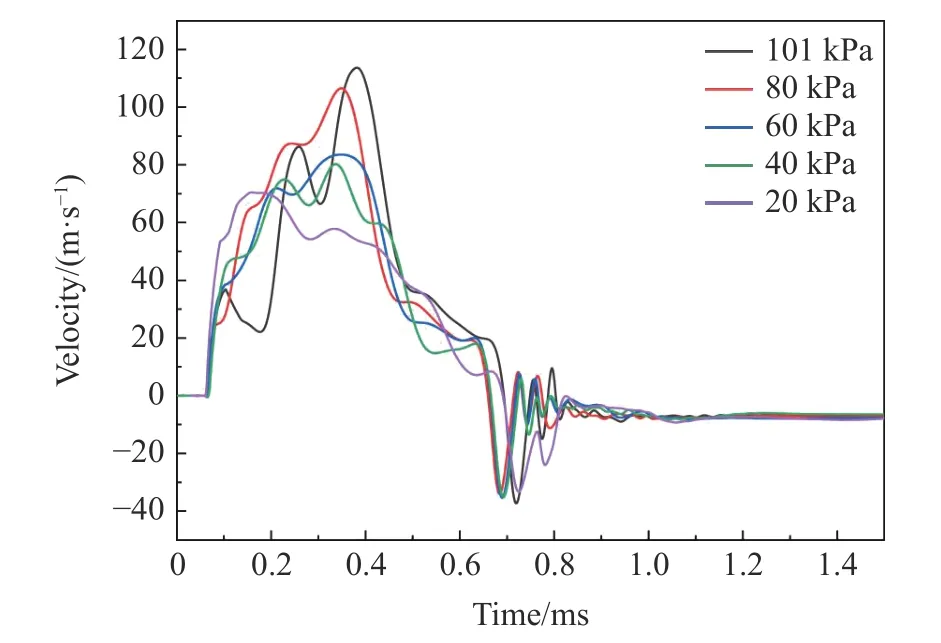
图7 钢板中心点速度曲线Fig.7 Velocity curves at center point of steel plate

数值模拟得到的钢板变形与实验结果一致，证明了数值模型的正确性。当初始环境压力为101、80、60 kPa 时，钢板中心点挠度的实验结果与数值模拟结果的相对误差分别为6.2%、0.4%、1.3%，两者符合得较好，但数值模拟结果整体偏小。这是因为实验中冲击波的传播过程还受空气温度和湿度影响，并且钢板螺栓孔处会出现轻微拉伸变形，导致钢板中心挠度的实验结果偏大。另外，数值模型无法完全模拟实验现实状态。考虑到挠度的相对误差小于10%，在可接受的范围之内，因此可以认为数值模型是正确、可靠的。